7.5.2三角形的内角和定理(2) 课件(共22张PPT)
文档属性
| 名称 | 7.5.2三角形的内角和定理(2) 课件(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 12:25:56 | ||
图片预览






文档简介
(共22张PPT)
7.5.2三角形的内角和定理(2)
第七章
平行线的证明
2021-2022学年八年级数学上册同步课件
学习目标
1. 会识别三角形的外角,并能运用三角形内角和定理及其两个推论进行简单的计算和证明.
2. 通过小组合作的方式,探索、证明与三角形外角有关的定理,体会一题多解的思维多样性和转化思想,提高总结概括和逻辑推理的能力.
导入新课
1、回顾三角形内角和定理.
2、三角形的边、角关系有哪些?
三角形
边的关系
角的关系
任意两边之和大于第三边
任意两边之差小于第三边
三角形三个内角的和等于180 °
导入新课
在一个三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时(方向与出发时相同),一共转了多少度?
想一想
讲授新课
三角形的外角的概念
一
观察:∠1 的两条边与△ABC的两条边有什么关系?
C
B
A
D
1
观察:∠1 的顶点与△ABC的顶点有什么关系?
①顶点是三角形的顶点;
②一条边是三角形内角的一边;
③另一条边是该内角另一条边的
反向延长线.
讲授新课
C
B
A
D
1
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC 的外角.
∠1 是△ABC的一个外角
讲授新课
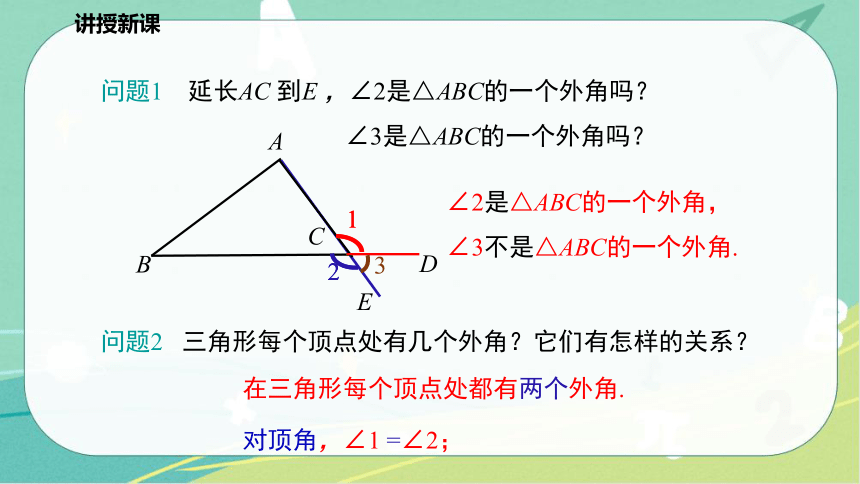
问题1 延长AC 到E ,∠2是△ABC的一个外角吗?
∠3是△ABC的一个外角吗?
E
在三角形每个顶点处都有两个外角.
对顶角,∠1 =∠2;
C
B
A
D
∠2是△ABC的一个外角,
∠3不是△ABC的一个外角.
问题2 三角形每个顶点处有几个外角?它们有怎样的关系?
1
2
3
2
1
讲授新课
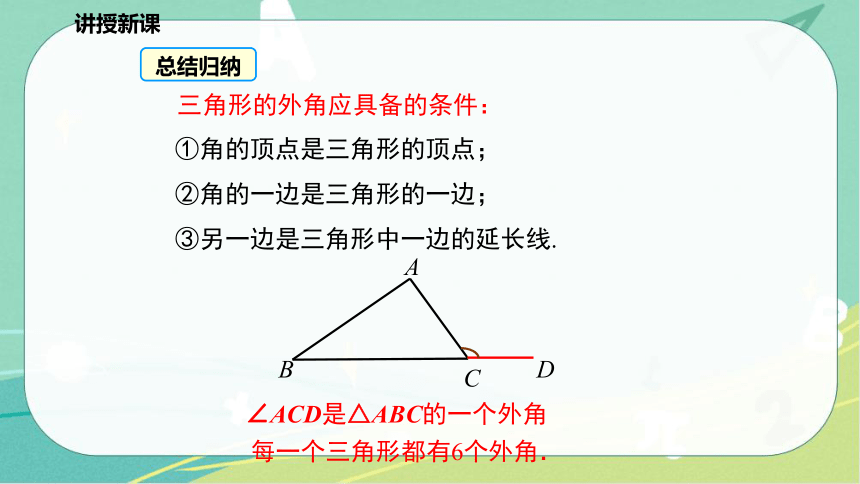
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个三角形都有6个外角.
总结归纳
讲授新课
F
A
B
C
D
E
如图,∠ BEC是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
∠AEC是哪个三角形的外角?
∠EFD是哪两个三角形的外角?
练一练
讲授新课
三角形的外角的性质
二
A
C
B
D
∠1=∠A+∠B
你能证明此结论吗?
观察:∠1 与△ABC的三个内角之间有什么关系?
∠1与∠2互补
1
2
∠1+∠2=180°(平角的定义).
∠1 > ∠A , ∠1> ∠B
讲授新课
已知:△ABC.
求证:∠ACD=∠A+∠B,
∠ACD>∠A,∠ACD>∠B.
证明:∵ ∠A+∠B+∠ACB=180°(三角形内角和定理)
∴∠A+∠B=180°-∠ACB(等式的性质),
∵ ∠ACD+∠ACB=180°(平角的定义)
∴∠ACD=180°-∠ACB(等式的性质)
∴∠ACD=∠A+∠B(等量代换)
∴∠ACD>∠A,∠ACD>∠B.
讲授新课
定理:三角形的一个外角大于任何一个与它
不相邻的内角.
A
B
C
符号语言:
归纳
三角形内角和定理有关外角的两个推论:
∵ ∠1 是△ABC 的外角
∴ ∠1=∠B+∠C
符号语言:
∵ ∠1 是△ABC 的外角
∴ ∠1 > ∠B, ∠1> ∠C
1
定理:三角形的一个外角等于与它不相邻的两个内角的和.
讲授新课
在这里,我们通过三角形的内角和定理直接推导出两个新定理.
像这样,由一个基本事实或定理直接推出的定理,叫做这个基本事实或定理的推论.推论可以当做定理使用.
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
讲授新课
例 如图,在△ABC中,∠B= ∠C,AD平分外角∠EAC.
求证:AD∥ BC.
A
C
D
B
E
例题运用了定理“内错角相等,两直线平行”
证明:∵∠EAC=∠B+∠C (三角形的一个
外角等于和它不相邻的两个内角的和),
∠B=∠C (已知),
2
3
1
∴∠C= ∠EAC (等式的性质).
∵AD平分 ∠EAC(已知).
∴∠DAC= ∠EAC(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴AD∥ BC(内错角相等,两直线平行).
讲授新课
例 如图,P是△ABC内一点,连接PB,PC.∠B= ∠C.
求证:∠BPC>∠A.
证明:如图,延长BP,交AC于点D.
∵ ∠BPC是△PDC的一个外角(外角定义),
∴ ∠BPC>∠PDC(三角形的一个外角
大于和它不相邻的任何一个内角).
∵ ∠PDC是△ABD的一个外角 (外角定义),
∴ ∠PDC>∠A
(三角形的一个外角大于和它不相邻的任何一个内角).
∴ ∠BPC>∠A .(不等式的性质)
A
B
C
P
D
还有其他证明方法吗?
当堂检测
1.如图,在△ABC中, D是BC延长线上一点,
∠B = 40°,∠ACD = 120°,
则∠A等于( )
A.60° B.70° C.80° D.90°
【解析】根据三角形外角的性质可得,∠ACD =∠B+∠A,所以∠A=∠ACD -∠B= 120°-40°= 80°.
C
当堂检测
2.如图,AB∥CD,则下列说法正确的是( )
A.∠3=2∠1+∠2
B.∠3=2∠1-∠2
C.∠3=∠1+∠2
D.∠3=180°-∠1-∠2
【解析】∵AB∥CD,∴∠1=∠BCD,∠3是△COD的外角,
∴∠3=∠2+∠BCD=∠2+∠1.
C
当堂检测
3.如图,直线a∥b,则∠ACB=_______.
【解析】延长BC交直线a于点D,
∵直线a∥b,
∴∠ADC=∠B=50°.
∵∠ACB是△ACD的外角,
∴∠ACB=∠A+∠ADC=28°+50°=78°.
78
当堂检测
4.如图,已知CE为△ABC外角∠ACD的平分线,CE交BA的延长线于点E,求证:∠BAC>∠B.
证明:∵CE平分∠ACD
∴∠1=∠2
∵∠BAC>∠1
∴∠BAC>∠2
∵∠2>∠B
∴∠BAC>∠B
课堂小结
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
1.三角形的外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
2.三角形的外角大于与它不相邻的任何一个内角
https://www.21cnjy.com/help/help_extract.php
7.5.2三角形的内角和定理(2)
第七章
平行线的证明
2021-2022学年八年级数学上册同步课件
学习目标
1. 会识别三角形的外角,并能运用三角形内角和定理及其两个推论进行简单的计算和证明.
2. 通过小组合作的方式,探索、证明与三角形外角有关的定理,体会一题多解的思维多样性和转化思想,提高总结概括和逻辑推理的能力.
导入新课
1、回顾三角形内角和定理.
2、三角形的边、角关系有哪些?
三角形
边的关系
角的关系
任意两边之和大于第三边
任意两边之差小于第三边
三角形三个内角的和等于180 °
导入新课
在一个三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时(方向与出发时相同),一共转了多少度?
想一想
讲授新课
三角形的外角的概念
一
观察:∠1 的两条边与△ABC的两条边有什么关系?
C
B
A
D
1
观察:∠1 的顶点与△ABC的顶点有什么关系?
①顶点是三角形的顶点;
②一条边是三角形内角的一边;
③另一条边是该内角另一条边的
反向延长线.
讲授新课
C
B
A
D
1
△ABC内角的一条边与另一条边的反向延长线组成的角,称为△ABC 的外角.
∠1 是△ABC的一个外角
讲授新课
问题1 延长AC 到E ,∠2是△ABC的一个外角吗?
∠3是△ABC的一个外角吗?
E
在三角形每个顶点处都有两个外角.
对顶角,∠1 =∠2;
C
B
A
D
∠2是△ABC的一个外角,
∠3不是△ABC的一个外角.
问题2 三角形每个顶点处有几个外角?它们有怎样的关系?
1
2
3
2
1
讲授新课
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个三角形都有6个外角.
总结归纳
讲授新课
F
A
B
C
D
E
如图,∠ BEC是哪个三角形的外角?
∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
∠AEC是哪个三角形的外角?
∠EFD是哪两个三角形的外角?
练一练
讲授新课
三角形的外角的性质
二
A
C
B
D
∠1=∠A+∠B
你能证明此结论吗?
观察:∠1 与△ABC的三个内角之间有什么关系?
∠1与∠2互补
1
2
∠1+∠2=180°(平角的定义).
∠1 > ∠A , ∠1> ∠B
讲授新课
已知:△ABC.
求证:∠ACD=∠A+∠B,
∠ACD>∠A,∠ACD>∠B.
证明:∵ ∠A+∠B+∠ACB=180°(三角形内角和定理)
∴∠A+∠B=180°-∠ACB(等式的性质),
∵ ∠ACD+∠ACB=180°(平角的定义)
∴∠ACD=180°-∠ACB(等式的性质)
∴∠ACD=∠A+∠B(等量代换)
∴∠ACD>∠A,∠ACD>∠B.
讲授新课
定理:三角形的一个外角大于任何一个与它
不相邻的内角.
A
B
C
符号语言:
归纳
三角形内角和定理有关外角的两个推论:
∵ ∠1 是△ABC 的外角
∴ ∠1=∠B+∠C
符号语言:
∵ ∠1 是△ABC 的外角
∴ ∠1 > ∠B, ∠1> ∠C
1
定理:三角形的一个外角等于与它不相邻的两个内角的和.
讲授新课
在这里,我们通过三角形的内角和定理直接推导出两个新定理.
像这样,由一个基本事实或定理直接推出的定理,叫做这个基本事实或定理的推论.推论可以当做定理使用.
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
讲授新课
例 如图,在△ABC中,∠B= ∠C,AD平分外角∠EAC.
求证:AD∥ BC.
A
C
D
B
E
例题运用了定理“内错角相等,两直线平行”
证明:∵∠EAC=∠B+∠C (三角形的一个
外角等于和它不相邻的两个内角的和),
∠B=∠C (已知),
2
3
1
∴∠C= ∠EAC (等式的性质).
∵AD平分 ∠EAC(已知).
∴∠DAC= ∠EAC(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴AD∥ BC(内错角相等,两直线平行).
讲授新课
例 如图,P是△ABC内一点,连接PB,PC.∠B= ∠C.
求证:∠BPC>∠A.
证明:如图,延长BP,交AC于点D.
∵ ∠BPC是△PDC的一个外角(外角定义),
∴ ∠BPC>∠PDC(三角形的一个外角
大于和它不相邻的任何一个内角).
∵ ∠PDC是△ABD的一个外角 (外角定义),
∴ ∠PDC>∠A
(三角形的一个外角大于和它不相邻的任何一个内角).
∴ ∠BPC>∠A .(不等式的性质)
A
B
C
P
D
还有其他证明方法吗?
当堂检测
1.如图,在△ABC中, D是BC延长线上一点,
∠B = 40°,∠ACD = 120°,
则∠A等于( )
A.60° B.70° C.80° D.90°
【解析】根据三角形外角的性质可得,∠ACD =∠B+∠A,所以∠A=∠ACD -∠B= 120°-40°= 80°.
C
当堂检测
2.如图,AB∥CD,则下列说法正确的是( )
A.∠3=2∠1+∠2
B.∠3=2∠1-∠2
C.∠3=∠1+∠2
D.∠3=180°-∠1-∠2
【解析】∵AB∥CD,∴∠1=∠BCD,∠3是△COD的外角,
∴∠3=∠2+∠BCD=∠2+∠1.
C
当堂检测
3.如图,直线a∥b,则∠ACB=_______.
【解析】延长BC交直线a于点D,
∵直线a∥b,
∴∠ADC=∠B=50°.
∵∠ACB是△ACD的外角,
∴∠ACB=∠A+∠ADC=28°+50°=78°.
78
当堂检测
4.如图,已知CE为△ABC外角∠ACD的平分线,CE交BA的延长线于点E,求证:∠BAC>∠B.
证明:∵CE平分∠ACD
∴∠1=∠2
∵∠BAC>∠1
∴∠BAC>∠2
∵∠2>∠B
∴∠BAC>∠B
课堂小结
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
1.三角形的外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
2.三角形的外角大于与它不相邻的任何一个内角
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
