1.5机械能守恒定律 自主提升过关练(word含解析)
文档属性
| 名称 | 1.5机械能守恒定律 自主提升过关练(word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-23 08:14:49 | ||
图片预览




文档简介
1.5机械能守恒定律 自主提升过关练(含解析)
一、选择题
1.在下列情况下机械能不守恒的有( )
A.在空气中匀速下落的降落伞 B.物体沿光滑圆弧面下滑
C.在空中做斜抛运动的铅球(不计空气阻力) D.沿光滑斜面下滑的物体
2.质量为的物体,竖直向下做匀变速直线运动,已知在内速度从增加到,则下列说法正确的是( )
A.该过程物体的机械能守恒
B.在内物体重力势能减少量为
C.物体除重力外,其他力的合外力为
D.物体在任意连续的两个内的位移差均为
3.小物块以一定的初速度沿斜面向上滑动,然后滑回到原处.设物块与斜面间的动摩擦因数不变,则该过程中,物块的动能Ek、重力势能Ep、机械能E、产生的内能Q与位移x关系图线正确的是( )
A. B.
C. D.
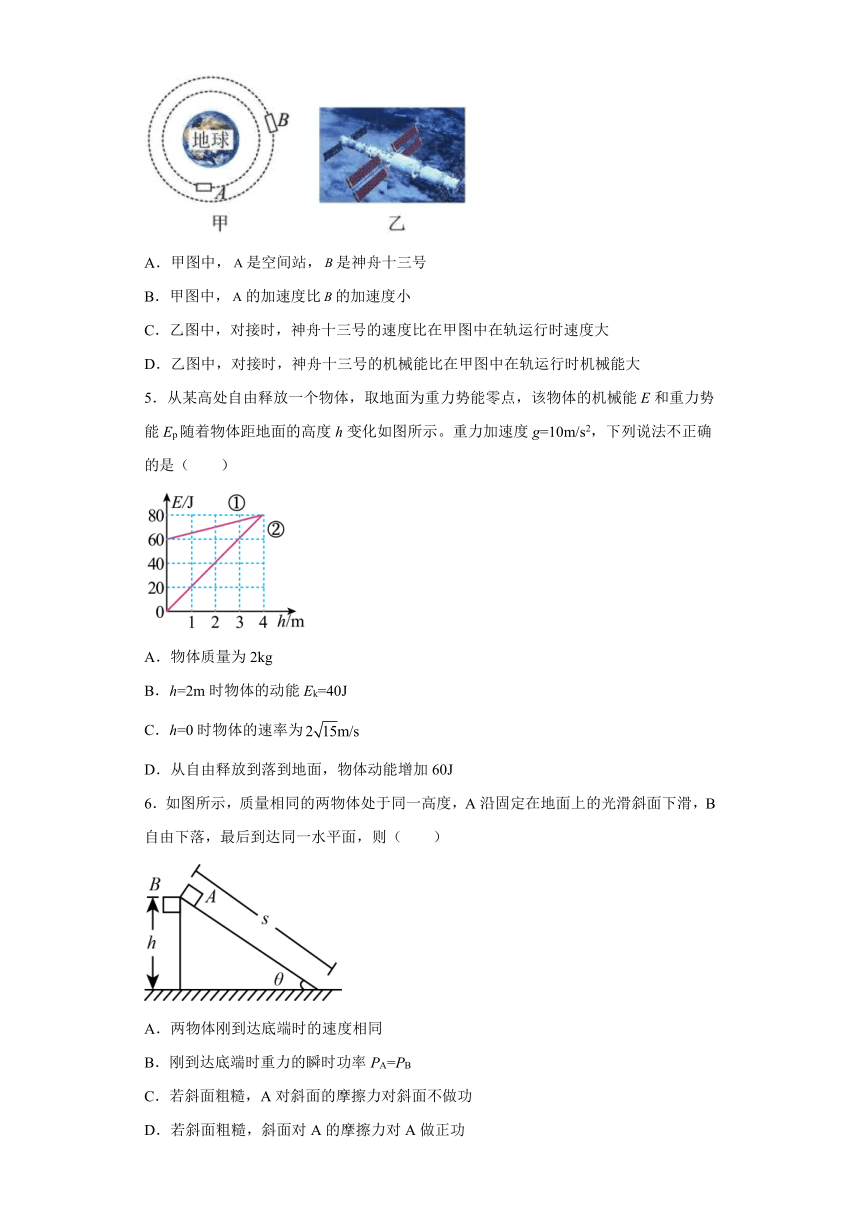
4.2021年10月16日,神舟十三号载人飞船在酒泉成功发射,并进入预定轨道,顺利将翟志刚、叶光富、王亚平3名航天员送入太空,飞船入轨后,按照预定程序,将通过加速与空间站进行自主快速交会对接.对接前,神舟十三号和空间站在轨运动的情形如图甲所示,对接时的情形如图乙所示,则下列说法正确的是( )
A.甲图中,是空间站,是神舟十三号
B.甲图中,的加速度比的加速度小
C.乙图中,对接时,神舟十三号的速度比在甲图中在轨运行时速度大
D.乙图中,对接时,神舟十三号的机械能比在甲图中在轨运行时机械能大
5.从某高处自由释放一个物体,取地面为重力势能零点,该物体的机械能E和重力势能Ep随着物体距地面的高度h变化如图所示。重力加速度g=10m/s2,下列说法不正确的是( )
A.物体质量为2kg
B.h=2m时物体的动能Ek=40J
C.h=0时物体的速率为
D.从自由释放到落到地面,物体动能增加60J
6.如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )
A.两物体刚到达底端时的速度相同
B.刚到达底端时重力的瞬时功率PA=PB
C.若斜面粗糙,A对斜面的摩擦力对斜面不做功
D.若斜面粗糙,斜面对A的摩擦力对A做正功
7.李刚同学将质量为m的实心球斜向上抛出(忽略空气阻力),出手后实心球在空中运动的轨迹如图所示.下列说法正确的是( )
A.上升时重力对球做正功,球的重力势能增大
B.落地前球具有的机械能始终不变
C.下落过程中球的动能、机械能均增大
D.球在最高点处的机械能为mgh(以地面为零势能面)
8.如图甲所示,足够长的传送带与水平面夹角为,传送带匀速转动,在传送带上某位置轻轻放置一滑块,滑块质量为m,滑块与传送带间的动摩擦因数为,滑块速度随时间变化的关系如图乙所示,、已知,则( )
A.传送带一定顺时针转动
B.的值可能为
C.传送带的速度大于
D.时刻因摩擦产生的热量为
9.图是跳高运动员奋力一跃成功跃过横杆的过程分解,试估算运动员在跃起过程中做的功大约为( )
A.7J B.70J C.700J D.7000J
10.如图所示,传送带以恒定速率v0顺时针运行。一个小物体无初速放在传送带底端,第一阶段物体被加速到与传送带具有相同的速度,第二阶段与传送带相对静止,匀速运动到达传送带顶端。下列说法中正确的是( )
A.第一阶段摩擦力对小物体做正功,第二阶段摩擦力对小物体不做功
B.第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加
C.第一阶段传送带克服摩擦力做功的功率逐渐增大
D.第一阶段物体和传送带间的摩擦生热等于第一阶段物体机械能的增加
11.长征途中,为了突破敌方关隘,战士爬上陡峭的山头,居高临下向敌方工事内投掷手榴弹。战士在同一位置先后投出甲、乙两颗质量均为m的手榴弹,手榴弹从投出的位置到落地点的高度差为h,在空中的运动可视为平抛运动,轨迹如图所示。重力加速度为g,下列说法正确的是( )
A.甲在空中的运动时间比乙的长
B.战士对两颗手榴弹做功一样多
C.两颗手榴弹在落地前瞬间,重力的功率相等
D.从投出到落地,每颗手榴弹的机械能变化量为
12.一质量为1kg的物体被人用手由静止向上提升1m,这时物体的速度为2m/s,则下列说法正确的是( )
A.手对物体做功10J B.合外力对物体做功12J
C.合外力对物体做功2J D.物体重力做正功10J
13.“天津之眼”是一座跨河建设、桥轮合一的摩天轮,是天津市的地标之一。摩天轮悬挂透明座舱,乘客随座舱在竖直面内做匀速圆周运动。下列叙述正确的是( )
A.摩天轮转动过程中,乘客的机械能保持不变
B.在最高点,乘客重力大于座椅对他的支持力
C.摩天轮转动过程中,座舱的速度不断变化
D.摩天轮转动过程中,乘客重力的瞬时功率保持不变
14.如图所示的装置中,木块M与地面间无摩擦,子弹m以一定的速度沿水平方向射入木块并留在其中,然后将弹簧压缩至最短。现将木块、子弹、弹簧作为研究对象,从子弹开始射入木块到弹簧压缩至最短的过程中,下列说法正确的是( )
A.系统的机械能守恒
B.子弹克服摩擦力做功等于系统产生的热量
C.弹簧压缩至最短时,系统的产生的热能小于子弹动能的减少量
D.弹簧压缩至最短时,子弹动能全部转化成弹簧的弹性势能
15.如图所示,一弯成“L”形的硬质轻杆可在竖直面内绕O点自由转动,已知两段轻杆的长度均为l,轻杆端点分别固定质量为m,2m的小球A、B(均可视为质点),现OA竖直,OB水平,静止释放,下列说法正确的是( )
A.B球运动到最低点时A球的速度为
B.A球某时刻速度可能为零
C.B球从释放至运动至最低点的过程中,轻杆对B球一直做正功
D.B球不可能运动至A球最初所在的位置
二、解答题
16.打井施工时采用如图所示的装置,将一质量可忽略不计的坚硬底座A送到井底。重锤B质量为m,下端固定一劲度系数为k的轻弹簧,弹簧下端距井口为,将B由静止释放,A被撞击后下沉时受到井壁的摩擦力,下沉的最大距离为,以后每次将B提升到原高度处静止释放,第n次撞击后,A恰能到达井底。已知重力加速度为g,不计空气阻力,弹簧始终在弹性限度内。
(1)求弹簧第一次刚接触A时B的速度v以及弹簧的最大形变量;
(2)第一次撞击后,若A刚开始下沉时弹簧弹性势能为,求此时B的动能;
(3)求井深H。
17.如图所示,一质量为m=2kg的小物块(可视为质点)以水平向右的初速度v1=5m/s,从A端滑上长为L=m的水平传送带,传送带以恒定速率v0=3m/s顺时针运动,小物块与传送带之间的动摩擦因数μ=0.5,传送带B端右侧的水平光滑轨道CDE与AB齐平,传送带与轨道之间的空隙可忽略不计。小物块每次进入CD之间时,会受到大小恒为2N、方向与运动方向相反、作用时间恒为△t=0.2s的阻力f,若小物块在CD之间的速率减为0时,阻力f会立即消失,CD之间的距离足够大。在DE之间的某个位置固定半径为R的竖直光滑圆形轨道,其外径略大于内径,重力加速度g=10m/s2。求∶
(1)小物块第一次向右经过B点的速率;
(2)若小物块第一次冲上圆形轨道后可到达E处,则R的取值范围;
(3)若R=0.8m,则在整个过程中,小物块与传送带之间由于摩擦产生的热量。
参考答案
1.A
【详解】
A.在空气中匀速下落的降落伞,动能不变,重力势能减少,则其机械能减少,机械能不守恒,A正确;
B.物体沿光滑圆弧面下滑,圆弧面对物体的支持力不做功,只有重力对物体做功,其机械能守恒,B错误;
C.在空中做斜抛运动的铅球,只受重力,机械能守恒,C错误;
D.沿光滑斜面下滑的物体,斜面对物体的支持力不做功,只有重力对物体做功,其机械能守恒,D错误。
故选A。
2.D
【详解】
A.根据加速度的定义可得
由此可知,物体除了受到重力之外,还受到阻力的作用,故机械能不守恒,A错误;
B.在内,物体下落的距离为
物体重力势能减少量为
B错误;
C.根据牛顿第二定律可得
解得
故物体除重力外,其他力的合外力为,C错误;
D.物体做匀加速直线运动,在连续的两个内的位移差为
D正确。
故选D。
3.D
【详解】
A.上滑时有
整理得
下滑时有
整理得
所以图A应该是线性图像为直线,所以A错误;
B.小物体从上滑后下滑,其位移先增大后减小,而图像B位移一直增大,所以B错误;
C.根据
由于摩擦力全程做负功,则机械能全程不断减小,而图C下滑过程机械能增加,所以C错误;
D.上滑时有
下滑时有
由数学知识可知,D正确;
故选D。
4.D
【详解】
A.对接时,神舟十三号在低轨道合适的位置加速做离心运动,到达天和核心舱所在的轨道与之对接,所以A是神舟十三号,B是天和核心舱,故A错误;
B.神舟十三号和天和核心舱绕地球做圆周运动,由万有引力提供向心力,由牛顿第二定律可知
可知加速度与轨道半径平方成反比,所以图(甲),A的加速度比B的加速度大,故B错误;
C.图(乙)中,对接时,神舟十三号所在的轨道半径比在图(甲)中所在的轨道半径大,由牛顿第二定律可得
所以图(甲)中神舟十三号的运行时速度比图(乙)中神舟十三号的运行时速度大,故C错误;
D.神舟十三号要从图(甲)的低轨道上升到图(乙)中的高轨道,需要点火加速,机械能增加,所以图(乙)中,对接时,神舟十三号的机械能比在图(甲)中在轨运行时机械能大,故D正确。
故选D。
5.B
【详解】
A.取地面为重力势能零点,由题图可知,物体在距地面高度为h=4m时,物体的重力势能为Ep=80J,由
Ep=mgh
可得
m=2kg
A正确,不符合题意;
B.h=2m时,物体的机械能是70J,物体的重力势能是40J,则有物体的动能为
Ek=70J-40J =30J
B错误,符合题意;
C.h=0时物体的重力势能是零,机械能等于动能,即是60J,则有
物体的速率为,C正确,不符合题意;
D.物体从自由释放时动能是零,到落到地面,物体的机械能是60J,重力势能是零,只有物体的动能,所以物体动能增加60J,D正确,不符合题意。
故选B。
6.C
【详解】
AB.由机械能守恒
可知,两物体到达斜面底端时的速度大小相等,但速度方向不同,B物体的重力的瞬时功率
A物体重力的瞬时功
AB错误;
C.若斜面粗糙,斜面受到摩擦力,但在摩擦力方向上无位移,故不做功,C正确;
D.物体受到的摩擦力沿斜面向上,位移沿斜面向下,对物体做负功,D错误。
故选C。
7.B
【详解】
A.上升时重力对球做负功,球的重力势能增大,故A错误;
B.因为运动中只有重力对球做功,则球的机械能守恒,即落地前球具有的机械能始终不变,故B正确;
C.下落过程中,重力做正功,动能增加,但机械能不变,故C错误;
D.球在最高点处还有动能,则在最高点的机械能大于mgh(以地面为零势能面),故D错误。
故选B。
8.B
【详解】
由图乙所示图象可知,滑块先做初速度为零的匀加速直线运动,在t0后以速度v0做匀速直线运动;由此可知
mgsinθ≤μmgcosθ
如果
mgsinθ>μmgcosθ
滑块在传送带上不会做匀速直线运动;
AC.如果传送带沿逆时针方向转动,滑块放在传送带上后受到的滑动摩擦力沿传送带向下,滑块先做匀加速直线运动,当滑块速度与传送带速度相等时滑块做匀速直线运动,则传送带的速度:v=v0;如果传送带沿顺时针方向转动,滑块刚放在传送带上时受到的滑动摩擦力沿斜面向上,滑块向上做匀加速直线运动,当滑块速度与传送带速度相等时滑块做匀速直线运动,传送带速度:v=v0;传送带速度不会大于v0,传送带即可能沿顺时针也可能沿逆时针方向转动,故AC错误;
B.由图乙所示图象可知,滑块做匀加速直线运动时的加速度
如果传送带沿逆时针方向转动,由牛顿第二定律得
mgsinθ+μmgcosθ=ma
解得
故B正确;
D.在t0时间内物块相对传送带的位移
则摩擦生热
选项D错误。
故选B。
9.C
【详解】
人站在地面时,设横杆到人体重心高度为1.1m,运动员质量为60kg。运动员起跳后相当于做上抛运动,则
故ABD错误,C正确。
故选C。
10.D
【详解】
A.第一阶段物体受到沿斜面向上的滑动摩擦力,则滑动摩擦力对小物体做正功,第二阶段物体受向上的静摩擦力,则静摩擦力对小物体也做正功,选项A错误;
B.第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加与重力势能的增加量之和,选项B错误;
C.根据
P=fv
可知,第一阶段传送带克服摩擦力做功的功率不变,选项C错误;
D.第一阶段物体的位移
传送带的位移
摩擦生热
物体机械能增量等于摩擦力做的正功,即
即第一阶段物体和传送带间的摩擦生热等于第一阶段物体机械能的增加,选项D正确。
故选D。
11.C
【详解】
A.根据,可得
甲、乙的下落高度相同,因此在空中的运动时间相等,故A错误;
B.根据,可得
甲、乙运动的水平位移s不同,因此水平初速度不同,说明获得的初动能不相等,由动能定理知战士对两颗手榴弹做功不相等,故B错误;
C.两颗手榴弹在落地前瞬间竖直方向的速度分量相等,重力的瞬时功率
相等,故C正确。
D.从投出到落地,只有重力做功,手榴弹的机械能保持不变,故D错误。
故选C。
12.C
【详解】
A.根据功能关系,可得手对物体做的功为
故A错误;
BC.根据动能定理,合外力对物体做功
故B错误,C正确;
D.物体克服重力做功
故D错误。
故选C。
13.BC
【详解】
A.摩天轮转动过程中,乘客的动能不变,重力势能变化,机械能不守恒,故A错误;
B.乘客在最高点时,由重力和座椅的支持力的合力提供向心力,而向心力方向向下,处于失重状态,则乘客重力大于座椅对他的支持力,故B正确;
C.摩天轮转动一周的过程中,座舱的速度大小不变,方向不断变化,所以座舱的速度不断变化,故C正确;
D.摩天轮转动过程中,乘客竖直方向的速度不断变化,则乘客重力的瞬时功率发生变化,故D错误。
故选BC。
14.C
【详解】
A.因为子弹进入木块的过程中,子弹需要克服摩擦力做功而产生内能,所以系统机械能不守恒,故A错误;
BCD.根据功能关系可知,从子弹开始射入木块到弹簧压缩至最短的过程中,子弹克服摩擦力做的功等于子弹动能的减少量;根据能量守恒定律可知,弹簧压缩至最短时,子弹减少的动能等于弹簧增加的弹性势能与系统产生的热量之和,故C正确,BD错误。
故选C。
15.ABD
【详解】
A.B球由释放运动到最低点时,由机械能守恒定律可知
解得
故A正确;
B.根据机械能守恒定律,当整个系统的重心回到原来的高度时,两球的总动能为零,此时两球的速度为零,故B正确;
C.B球从释放至运动至最低点的过程中,根据动能定理
解得
W=0
可知B球从释放至运动至最低点的过程中,轻杆对B球做的功为0,故C错误;
D.若B球恰能运动至A球最初所在的位置,则整个系统的重力势能增加,即机械能增加,则不可能,故D正确。
故选ABD。
16.(1),;(2)(答也算对);(3)
【详解】
(1)根据自由落体运动规律可得
由于A质量不计,所以其合力为零,根据平衡条件有
解得
(2)从B开始下落到A刚开始运动的过程中,根据机械能守恒定律得
解得
另解:在B和A一起下沉的过程中,根据能量守恒定律得
解得
(3)对A的第一次下沉,根据能量守恒定律有
对A的第二次下沉,根据能量守恒有
解得
对A的第三次下沉,根据能量守恒定律有
解得
可推知A第n次下沉过程中向下滑动的距离为
所以
17.(1) 3.5m/s;(2) ;(3) 158.56J
【详解】
(1)若小物块可与传送带共速,则对小物块有
解得
故小物块一直做匀减速直线运动
设小物块第一次向右经过B处的速率为,对小物块从A→B过程中有
解得
=3.5m/s
(2)对小物块从B→D过程中,小物块的加速度大小
由匀变速直线运动公式有
由于可到达E处,故小物块到达圆轨道最高点的线速度要大于0,即
解得
(3)对小物块从A→B过程中有
解得
t0=0.3s
该过程中,传送带的位移
x传0=v0t0=0.9m
小物块与传送带之间由于摩擦产生的热量
Q0=μmg(L-x传0)=3.75J
由于
故小物块每次从D处冲上圆轨道后都会返回D处。设小物块第一次向左返回B处的速率为,则从小物块第一次向右经过B处到第一次向左返回B处过程中有
由题意知,小物块第一次从B处向左冲上传送带后,不会从传送带的左端冲出。易知小物块第二次向右经过B处的速率vB2=3m/s
从小物块第一次向左经过B处到小物块与传送带共速的过程中,取向左为正方向,则有
小物块向左的位移
传送带向右的位移
小物块与传送带之间由于摩擦产生的热量
Q1=μmg(x物1+x传1)=37.21J
此后设小物块第n次(n≥2)向左返回B处的速率为,从小物块第n次向右经过B处到第n次向左返回B处过程中有
易知小物块第n次从B处向左冲上传送带后又会原速率返回B处,即小物块第n+1次向右经过B处的速率
小物块从B处第n次向左冲上传送带到第n+1次向右离开传送带的过程中,取向左为正方向,则有
小物块相对传送带左滑的距离
小物块与传送带之间由于摩擦产生的热量
(n≥2)
由=3.4-0.4n可知,小物块第8次向左返回B处的速率
=(3.4-0.4×8)m/s=0.2m/s
小物块第8次从B处向左冲上传送带后又会原速率返回B处,即小物块第9次向右经过B处的速率
vB9==0.2m/s
故小物块第9次向右进入CD区间后,恰好经过Δt=0.2s停下,此后将不再受力
小物块第2次从B处向左冲上传送带到第9次向右经过B处的过程中,小物块与传送带之间由于摩擦产生的热量
Q=Q2+Q3+…+Q8=[40.8×7-4.8×(2+3+…+8)]J=117.6J
整个过程中,小物块与传送带之间由于摩擦产生的热量
Q总=Q0+Q1+Q=158.56J
一、选择题
1.在下列情况下机械能不守恒的有( )
A.在空气中匀速下落的降落伞 B.物体沿光滑圆弧面下滑
C.在空中做斜抛运动的铅球(不计空气阻力) D.沿光滑斜面下滑的物体
2.质量为的物体,竖直向下做匀变速直线运动,已知在内速度从增加到,则下列说法正确的是( )
A.该过程物体的机械能守恒
B.在内物体重力势能减少量为
C.物体除重力外,其他力的合外力为
D.物体在任意连续的两个内的位移差均为
3.小物块以一定的初速度沿斜面向上滑动,然后滑回到原处.设物块与斜面间的动摩擦因数不变,则该过程中,物块的动能Ek、重力势能Ep、机械能E、产生的内能Q与位移x关系图线正确的是( )
A. B.
C. D.
4.2021年10月16日,神舟十三号载人飞船在酒泉成功发射,并进入预定轨道,顺利将翟志刚、叶光富、王亚平3名航天员送入太空,飞船入轨后,按照预定程序,将通过加速与空间站进行自主快速交会对接.对接前,神舟十三号和空间站在轨运动的情形如图甲所示,对接时的情形如图乙所示,则下列说法正确的是( )
A.甲图中,是空间站,是神舟十三号
B.甲图中,的加速度比的加速度小
C.乙图中,对接时,神舟十三号的速度比在甲图中在轨运行时速度大
D.乙图中,对接时,神舟十三号的机械能比在甲图中在轨运行时机械能大
5.从某高处自由释放一个物体,取地面为重力势能零点,该物体的机械能E和重力势能Ep随着物体距地面的高度h变化如图所示。重力加速度g=10m/s2,下列说法不正确的是( )
A.物体质量为2kg
B.h=2m时物体的动能Ek=40J
C.h=0时物体的速率为
D.从自由释放到落到地面,物体动能增加60J
6.如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )
A.两物体刚到达底端时的速度相同
B.刚到达底端时重力的瞬时功率PA=PB
C.若斜面粗糙,A对斜面的摩擦力对斜面不做功
D.若斜面粗糙,斜面对A的摩擦力对A做正功
7.李刚同学将质量为m的实心球斜向上抛出(忽略空气阻力),出手后实心球在空中运动的轨迹如图所示.下列说法正确的是( )
A.上升时重力对球做正功,球的重力势能增大
B.落地前球具有的机械能始终不变
C.下落过程中球的动能、机械能均增大
D.球在最高点处的机械能为mgh(以地面为零势能面)
8.如图甲所示,足够长的传送带与水平面夹角为,传送带匀速转动,在传送带上某位置轻轻放置一滑块,滑块质量为m,滑块与传送带间的动摩擦因数为,滑块速度随时间变化的关系如图乙所示,、已知,则( )
A.传送带一定顺时针转动
B.的值可能为
C.传送带的速度大于
D.时刻因摩擦产生的热量为
9.图是跳高运动员奋力一跃成功跃过横杆的过程分解,试估算运动员在跃起过程中做的功大约为( )
A.7J B.70J C.700J D.7000J
10.如图所示,传送带以恒定速率v0顺时针运行。一个小物体无初速放在传送带底端,第一阶段物体被加速到与传送带具有相同的速度,第二阶段与传送带相对静止,匀速运动到达传送带顶端。下列说法中正确的是( )
A.第一阶段摩擦力对小物体做正功,第二阶段摩擦力对小物体不做功
B.第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加
C.第一阶段传送带克服摩擦力做功的功率逐渐增大
D.第一阶段物体和传送带间的摩擦生热等于第一阶段物体机械能的增加
11.长征途中,为了突破敌方关隘,战士爬上陡峭的山头,居高临下向敌方工事内投掷手榴弹。战士在同一位置先后投出甲、乙两颗质量均为m的手榴弹,手榴弹从投出的位置到落地点的高度差为h,在空中的运动可视为平抛运动,轨迹如图所示。重力加速度为g,下列说法正确的是( )
A.甲在空中的运动时间比乙的长
B.战士对两颗手榴弹做功一样多
C.两颗手榴弹在落地前瞬间,重力的功率相等
D.从投出到落地,每颗手榴弹的机械能变化量为
12.一质量为1kg的物体被人用手由静止向上提升1m,这时物体的速度为2m/s,则下列说法正确的是( )
A.手对物体做功10J B.合外力对物体做功12J
C.合外力对物体做功2J D.物体重力做正功10J
13.“天津之眼”是一座跨河建设、桥轮合一的摩天轮,是天津市的地标之一。摩天轮悬挂透明座舱,乘客随座舱在竖直面内做匀速圆周运动。下列叙述正确的是( )
A.摩天轮转动过程中,乘客的机械能保持不变
B.在最高点,乘客重力大于座椅对他的支持力
C.摩天轮转动过程中,座舱的速度不断变化
D.摩天轮转动过程中,乘客重力的瞬时功率保持不变
14.如图所示的装置中,木块M与地面间无摩擦,子弹m以一定的速度沿水平方向射入木块并留在其中,然后将弹簧压缩至最短。现将木块、子弹、弹簧作为研究对象,从子弹开始射入木块到弹簧压缩至最短的过程中,下列说法正确的是( )
A.系统的机械能守恒
B.子弹克服摩擦力做功等于系统产生的热量
C.弹簧压缩至最短时,系统的产生的热能小于子弹动能的减少量
D.弹簧压缩至最短时,子弹动能全部转化成弹簧的弹性势能
15.如图所示,一弯成“L”形的硬质轻杆可在竖直面内绕O点自由转动,已知两段轻杆的长度均为l,轻杆端点分别固定质量为m,2m的小球A、B(均可视为质点),现OA竖直,OB水平,静止释放,下列说法正确的是( )
A.B球运动到最低点时A球的速度为
B.A球某时刻速度可能为零
C.B球从释放至运动至最低点的过程中,轻杆对B球一直做正功
D.B球不可能运动至A球最初所在的位置
二、解答题
16.打井施工时采用如图所示的装置,将一质量可忽略不计的坚硬底座A送到井底。重锤B质量为m,下端固定一劲度系数为k的轻弹簧,弹簧下端距井口为,将B由静止释放,A被撞击后下沉时受到井壁的摩擦力,下沉的最大距离为,以后每次将B提升到原高度处静止释放,第n次撞击后,A恰能到达井底。已知重力加速度为g,不计空气阻力,弹簧始终在弹性限度内。
(1)求弹簧第一次刚接触A时B的速度v以及弹簧的最大形变量;
(2)第一次撞击后,若A刚开始下沉时弹簧弹性势能为,求此时B的动能;
(3)求井深H。
17.如图所示,一质量为m=2kg的小物块(可视为质点)以水平向右的初速度v1=5m/s,从A端滑上长为L=m的水平传送带,传送带以恒定速率v0=3m/s顺时针运动,小物块与传送带之间的动摩擦因数μ=0.5,传送带B端右侧的水平光滑轨道CDE与AB齐平,传送带与轨道之间的空隙可忽略不计。小物块每次进入CD之间时,会受到大小恒为2N、方向与运动方向相反、作用时间恒为△t=0.2s的阻力f,若小物块在CD之间的速率减为0时,阻力f会立即消失,CD之间的距离足够大。在DE之间的某个位置固定半径为R的竖直光滑圆形轨道,其外径略大于内径,重力加速度g=10m/s2。求∶
(1)小物块第一次向右经过B点的速率;
(2)若小物块第一次冲上圆形轨道后可到达E处,则R的取值范围;
(3)若R=0.8m,则在整个过程中,小物块与传送带之间由于摩擦产生的热量。
参考答案
1.A
【详解】
A.在空气中匀速下落的降落伞,动能不变,重力势能减少,则其机械能减少,机械能不守恒,A正确;
B.物体沿光滑圆弧面下滑,圆弧面对物体的支持力不做功,只有重力对物体做功,其机械能守恒,B错误;
C.在空中做斜抛运动的铅球,只受重力,机械能守恒,C错误;
D.沿光滑斜面下滑的物体,斜面对物体的支持力不做功,只有重力对物体做功,其机械能守恒,D错误。
故选A。
2.D
【详解】
A.根据加速度的定义可得
由此可知,物体除了受到重力之外,还受到阻力的作用,故机械能不守恒,A错误;
B.在内,物体下落的距离为
物体重力势能减少量为
B错误;
C.根据牛顿第二定律可得
解得
故物体除重力外,其他力的合外力为,C错误;
D.物体做匀加速直线运动,在连续的两个内的位移差为
D正确。
故选D。
3.D
【详解】
A.上滑时有
整理得
下滑时有
整理得
所以图A应该是线性图像为直线,所以A错误;
B.小物体从上滑后下滑,其位移先增大后减小,而图像B位移一直增大,所以B错误;
C.根据
由于摩擦力全程做负功,则机械能全程不断减小,而图C下滑过程机械能增加,所以C错误;
D.上滑时有
下滑时有
由数学知识可知,D正确;
故选D。
4.D
【详解】
A.对接时,神舟十三号在低轨道合适的位置加速做离心运动,到达天和核心舱所在的轨道与之对接,所以A是神舟十三号,B是天和核心舱,故A错误;
B.神舟十三号和天和核心舱绕地球做圆周运动,由万有引力提供向心力,由牛顿第二定律可知
可知加速度与轨道半径平方成反比,所以图(甲),A的加速度比B的加速度大,故B错误;
C.图(乙)中,对接时,神舟十三号所在的轨道半径比在图(甲)中所在的轨道半径大,由牛顿第二定律可得
所以图(甲)中神舟十三号的运行时速度比图(乙)中神舟十三号的运行时速度大,故C错误;
D.神舟十三号要从图(甲)的低轨道上升到图(乙)中的高轨道,需要点火加速,机械能增加,所以图(乙)中,对接时,神舟十三号的机械能比在图(甲)中在轨运行时机械能大,故D正确。
故选D。
5.B
【详解】
A.取地面为重力势能零点,由题图可知,物体在距地面高度为h=4m时,物体的重力势能为Ep=80J,由
Ep=mgh
可得
m=2kg
A正确,不符合题意;
B.h=2m时,物体的机械能是70J,物体的重力势能是40J,则有物体的动能为
Ek=70J-40J =30J
B错误,符合题意;
C.h=0时物体的重力势能是零,机械能等于动能,即是60J,则有
物体的速率为,C正确,不符合题意;
D.物体从自由释放时动能是零,到落到地面,物体的机械能是60J,重力势能是零,只有物体的动能,所以物体动能增加60J,D正确,不符合题意。
故选B。
6.C
【详解】
AB.由机械能守恒
可知,两物体到达斜面底端时的速度大小相等,但速度方向不同,B物体的重力的瞬时功率
A物体重力的瞬时功
AB错误;
C.若斜面粗糙,斜面受到摩擦力,但在摩擦力方向上无位移,故不做功,C正确;
D.物体受到的摩擦力沿斜面向上,位移沿斜面向下,对物体做负功,D错误。
故选C。
7.B
【详解】
A.上升时重力对球做负功,球的重力势能增大,故A错误;
B.因为运动中只有重力对球做功,则球的机械能守恒,即落地前球具有的机械能始终不变,故B正确;
C.下落过程中,重力做正功,动能增加,但机械能不变,故C错误;
D.球在最高点处还有动能,则在最高点的机械能大于mgh(以地面为零势能面),故D错误。
故选B。
8.B
【详解】
由图乙所示图象可知,滑块先做初速度为零的匀加速直线运动,在t0后以速度v0做匀速直线运动;由此可知
mgsinθ≤μmgcosθ
如果
mgsinθ>μmgcosθ
滑块在传送带上不会做匀速直线运动;
AC.如果传送带沿逆时针方向转动,滑块放在传送带上后受到的滑动摩擦力沿传送带向下,滑块先做匀加速直线运动,当滑块速度与传送带速度相等时滑块做匀速直线运动,则传送带的速度:v=v0;如果传送带沿顺时针方向转动,滑块刚放在传送带上时受到的滑动摩擦力沿斜面向上,滑块向上做匀加速直线运动,当滑块速度与传送带速度相等时滑块做匀速直线运动,传送带速度:v=v0;传送带速度不会大于v0,传送带即可能沿顺时针也可能沿逆时针方向转动,故AC错误;
B.由图乙所示图象可知,滑块做匀加速直线运动时的加速度
如果传送带沿逆时针方向转动,由牛顿第二定律得
mgsinθ+μmgcosθ=ma
解得
故B正确;
D.在t0时间内物块相对传送带的位移
则摩擦生热
选项D错误。
故选B。
9.C
【详解】
人站在地面时,设横杆到人体重心高度为1.1m,运动员质量为60kg。运动员起跳后相当于做上抛运动,则
故ABD错误,C正确。
故选C。
10.D
【详解】
A.第一阶段物体受到沿斜面向上的滑动摩擦力,则滑动摩擦力对小物体做正功,第二阶段物体受向上的静摩擦力,则静摩擦力对小物体也做正功,选项A错误;
B.第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加与重力势能的增加量之和,选项B错误;
C.根据
P=fv
可知,第一阶段传送带克服摩擦力做功的功率不变,选项C错误;
D.第一阶段物体的位移
传送带的位移
摩擦生热
物体机械能增量等于摩擦力做的正功,即
即第一阶段物体和传送带间的摩擦生热等于第一阶段物体机械能的增加,选项D正确。
故选D。
11.C
【详解】
A.根据,可得
甲、乙的下落高度相同,因此在空中的运动时间相等,故A错误;
B.根据,可得
甲、乙运动的水平位移s不同,因此水平初速度不同,说明获得的初动能不相等,由动能定理知战士对两颗手榴弹做功不相等,故B错误;
C.两颗手榴弹在落地前瞬间竖直方向的速度分量相等,重力的瞬时功率
相等,故C正确。
D.从投出到落地,只有重力做功,手榴弹的机械能保持不变,故D错误。
故选C。
12.C
【详解】
A.根据功能关系,可得手对物体做的功为
故A错误;
BC.根据动能定理,合外力对物体做功
故B错误,C正确;
D.物体克服重力做功
故D错误。
故选C。
13.BC
【详解】
A.摩天轮转动过程中,乘客的动能不变,重力势能变化,机械能不守恒,故A错误;
B.乘客在最高点时,由重力和座椅的支持力的合力提供向心力,而向心力方向向下,处于失重状态,则乘客重力大于座椅对他的支持力,故B正确;
C.摩天轮转动一周的过程中,座舱的速度大小不变,方向不断变化,所以座舱的速度不断变化,故C正确;
D.摩天轮转动过程中,乘客竖直方向的速度不断变化,则乘客重力的瞬时功率发生变化,故D错误。
故选BC。
14.C
【详解】
A.因为子弹进入木块的过程中,子弹需要克服摩擦力做功而产生内能,所以系统机械能不守恒,故A错误;
BCD.根据功能关系可知,从子弹开始射入木块到弹簧压缩至最短的过程中,子弹克服摩擦力做的功等于子弹动能的减少量;根据能量守恒定律可知,弹簧压缩至最短时,子弹减少的动能等于弹簧增加的弹性势能与系统产生的热量之和,故C正确,BD错误。
故选C。
15.ABD
【详解】
A.B球由释放运动到最低点时,由机械能守恒定律可知
解得
故A正确;
B.根据机械能守恒定律,当整个系统的重心回到原来的高度时,两球的总动能为零,此时两球的速度为零,故B正确;
C.B球从释放至运动至最低点的过程中,根据动能定理
解得
W=0
可知B球从释放至运动至最低点的过程中,轻杆对B球做的功为0,故C错误;
D.若B球恰能运动至A球最初所在的位置,则整个系统的重力势能增加,即机械能增加,则不可能,故D正确。
故选ABD。
16.(1),;(2)(答也算对);(3)
【详解】
(1)根据自由落体运动规律可得
由于A质量不计,所以其合力为零,根据平衡条件有
解得
(2)从B开始下落到A刚开始运动的过程中,根据机械能守恒定律得
解得
另解:在B和A一起下沉的过程中,根据能量守恒定律得
解得
(3)对A的第一次下沉,根据能量守恒定律有
对A的第二次下沉,根据能量守恒有
解得
对A的第三次下沉,根据能量守恒定律有
解得
可推知A第n次下沉过程中向下滑动的距离为
所以
17.(1) 3.5m/s;(2) ;(3) 158.56J
【详解】
(1)若小物块可与传送带共速,则对小物块有
解得
故小物块一直做匀减速直线运动
设小物块第一次向右经过B处的速率为,对小物块从A→B过程中有
解得
=3.5m/s
(2)对小物块从B→D过程中,小物块的加速度大小
由匀变速直线运动公式有
由于可到达E处,故小物块到达圆轨道最高点的线速度要大于0,即
解得
(3)对小物块从A→B过程中有
解得
t0=0.3s
该过程中,传送带的位移
x传0=v0t0=0.9m
小物块与传送带之间由于摩擦产生的热量
Q0=μmg(L-x传0)=3.75J
由于
故小物块每次从D处冲上圆轨道后都会返回D处。设小物块第一次向左返回B处的速率为,则从小物块第一次向右经过B处到第一次向左返回B处过程中有
由题意知,小物块第一次从B处向左冲上传送带后,不会从传送带的左端冲出。易知小物块第二次向右经过B处的速率vB2=3m/s
从小物块第一次向左经过B处到小物块与传送带共速的过程中,取向左为正方向,则有
小物块向左的位移
传送带向右的位移
小物块与传送带之间由于摩擦产生的热量
Q1=μmg(x物1+x传1)=37.21J
此后设小物块第n次(n≥2)向左返回B处的速率为,从小物块第n次向右经过B处到第n次向左返回B处过程中有
易知小物块第n次从B处向左冲上传送带后又会原速率返回B处,即小物块第n+1次向右经过B处的速率
小物块从B处第n次向左冲上传送带到第n+1次向右离开传送带的过程中,取向左为正方向,则有
小物块相对传送带左滑的距离
小物块与传送带之间由于摩擦产生的热量
(n≥2)
由=3.4-0.4n可知,小物块第8次向左返回B处的速率
=(3.4-0.4×8)m/s=0.2m/s
小物块第8次从B处向左冲上传送带后又会原速率返回B处,即小物块第9次向右经过B处的速率
vB9==0.2m/s
故小物块第9次向右进入CD区间后,恰好经过Δt=0.2s停下,此后将不再受力
小物块第2次从B处向左冲上传送带到第9次向右经过B处的过程中,小物块与传送带之间由于摩擦产生的热量
Q=Q2+Q3+…+Q8=[40.8×7-4.8×(2+3+…+8)]J=117.6J
整个过程中,小物块与传送带之间由于摩擦产生的热量
Q总=Q0+Q1+Q=158.56J
同课章节目录
