鸡兔同笼(导学案)人教版 数学四年级下册
文档属性
| 名称 | 鸡兔同笼(导学案)人教版 数学四年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 44.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 00:00:00 | ||
图片预览


文档简介
学习目标:
1.了解”鸡兔同笼”问题,感受中国古代数学问题的趣味性;
2.尝试列表枚举,图示,假设等不同的方法解决”鸡兔同笼”问题,体验解决问题方法的多
样性,提高解决实际问题的能力;
3.通过自主探索,合作交流,培养合作意识和逻辑推理能力;
4.体会数学问题在日常生活中的应用,进而体会数学的价值.
重点:1.用列表法解决实际问题;
2. 理解“鸡兔同笼”问题中的数量关系;
难点:1.在解决问题的过程中培养学生的逻辑思维能力.
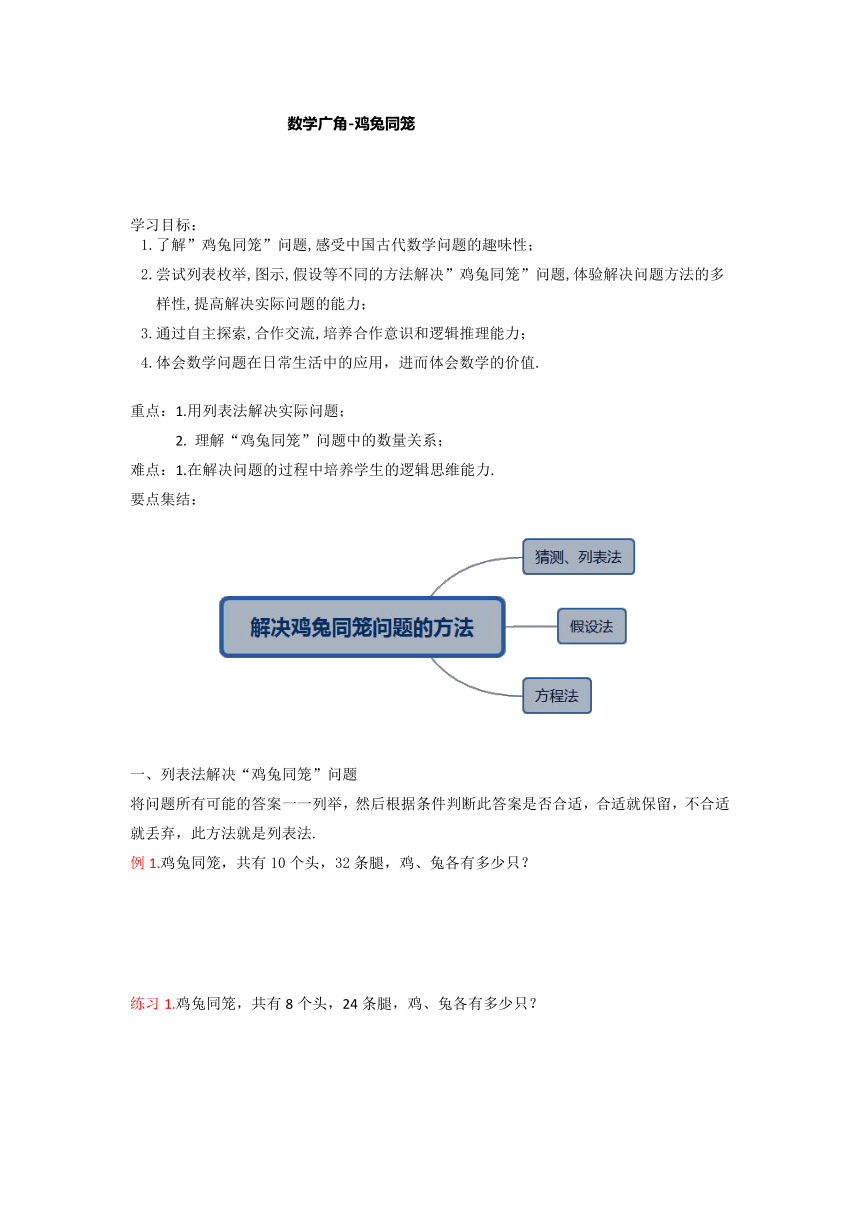
要点集结:
一、列表法解决“鸡兔同笼”问题
将问题所有可能的答案一一列举,然后根据条件判断此答案是否合适,合适就保留,不合适就丢弃,此方法就是列表法.
例1.鸡兔同笼,共有10个头,32条腿,鸡、兔各有多少只?
练习1.鸡兔同笼,共有8个头,24条腿,鸡、兔各有多少只?
小结:
当头数较少时,可以逐一列举,直到列举出的腿数和题目中的腿数相同.
例2.“今有鸡兔同笼,上有30头,下有88足,问鸡兔各几何?”你能解决这个古代数学问题吗?
练习1.在一个圈中只有鸭和鹿,共有29个头,90条腿.鸭和鹿各有几只?
小结:
根据条件得不同,可以采用逐一列举的方法;或先估计数量的可能范围,以减少列举的次数.
二、假设法解决“鸡兔同笼”问题
例1.小梅数她家的鸡与兔,数头有16个,数脚有44只.问:小梅家的鸡与兔各有多少只
练习1.鸡兔同笼,共23头,共68足,鸡、兔有各几只?
小结:
①假设笼子里全是鸡: 兔的只数=(实际脚数-2鸡兔的总只数)(4-2)
鸡的只数=鸡兔的总只数-兔的只数
②假设笼子里全是兔: 鸡的只数=(4鸡兔的总只数-实际脚数)(4-2)
兔的只数=鸡兔的总只数-鸡的只数
例2.100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人
练习1.学校有象棋、跳棋共26副,2人下一副象棋,6人下一副跳棋,恰好可供120个学生进行活动.问:象棋与跳棋各有多少副?
小结:
此类题目的解法为:将题目中的信息对应地转化为鸡兔同笼里的三个信息:1、一只鸡、兔的腿数;2、鸡兔总头数;3、鸡兔总腿数,然后假设法去解决.
例3.灯泡厂生产灯泡的工人,按得分的多少给工资.每生产一个合格品记4分,每生产一个不合格品不仅不记分,还要扣除15分.某工人生产了1000只灯泡,共得3525分,问其中有多少个灯泡不合格?”
练习1.某次数学竞赛共20道题,评分标准是每做对一题得5分,每做错一题倒扣1分.刘亮参加了这次竞赛,得了64分.刘亮做对了多少道题?
小结:
假设法解此类题目时要理解“做对一题得5分”和“做错一题倒扣1分”之间的差距是几分,可以借助线段图理解.
三、方程法解决“鸡兔同笼”问题(选学)
例1.鸡、兔共有头100个,脚350只,鸡、兔各有多少只
练习1.鸡兔共有56只,212条腿,问鸡、兔各有几只?
小结:
列方程的等量关系式:鸡的只数2+兔的只数4=鸡兔的总脚数
例2.彩色文化用品每套19元,普通文化用品每套11元,这两种文化用品共买了16套,用钱280元.问:两种文化用品各买了多少套?
练习1.面值是2元、5元的人民币共27张,全计99元.面值是2元、5元的人民币各有多少张?
小结:
此类题目只是变换情景,方法与例1方法相同.
总结:
1.列举法:若鸡兔总头数较少时,可逐一列举;若鸡兔总头数较多时,可以先进行估算,然后跳跃列举.
2.假设法解“鸡兔同笼”问题的公式:
①假设笼子里全是鸡: 兔的只数=(实际脚数-2鸡兔的总只数)(4-2)
鸡的只数=鸡兔的总只数-兔的只数
②假设笼子里全是兔: 鸡的只数=(4鸡兔的总只数-实际脚数)(4-2)
兔的只数=鸡兔的总只数-鸡的只数
方程法:等量关系式:鸡的只数2+兔的只数4=鸡兔的总脚数
1.了解”鸡兔同笼”问题,感受中国古代数学问题的趣味性;
2.尝试列表枚举,图示,假设等不同的方法解决”鸡兔同笼”问题,体验解决问题方法的多
样性,提高解决实际问题的能力;
3.通过自主探索,合作交流,培养合作意识和逻辑推理能力;
4.体会数学问题在日常生活中的应用,进而体会数学的价值.
重点:1.用列表法解决实际问题;
2. 理解“鸡兔同笼”问题中的数量关系;
难点:1.在解决问题的过程中培养学生的逻辑思维能力.
要点集结:
一、列表法解决“鸡兔同笼”问题
将问题所有可能的答案一一列举,然后根据条件判断此答案是否合适,合适就保留,不合适就丢弃,此方法就是列表法.
例1.鸡兔同笼,共有10个头,32条腿,鸡、兔各有多少只?
练习1.鸡兔同笼,共有8个头,24条腿,鸡、兔各有多少只?
小结:
当头数较少时,可以逐一列举,直到列举出的腿数和题目中的腿数相同.
例2.“今有鸡兔同笼,上有30头,下有88足,问鸡兔各几何?”你能解决这个古代数学问题吗?
练习1.在一个圈中只有鸭和鹿,共有29个头,90条腿.鸭和鹿各有几只?
小结:
根据条件得不同,可以采用逐一列举的方法;或先估计数量的可能范围,以减少列举的次数.
二、假设法解决“鸡兔同笼”问题
例1.小梅数她家的鸡与兔,数头有16个,数脚有44只.问:小梅家的鸡与兔各有多少只
练习1.鸡兔同笼,共23头,共68足,鸡、兔有各几只?
小结:
①假设笼子里全是鸡: 兔的只数=(实际脚数-2鸡兔的总只数)(4-2)
鸡的只数=鸡兔的总只数-兔的只数
②假设笼子里全是兔: 鸡的只数=(4鸡兔的总只数-实际脚数)(4-2)
兔的只数=鸡兔的总只数-鸡的只数
例2.100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人
练习1.学校有象棋、跳棋共26副,2人下一副象棋,6人下一副跳棋,恰好可供120个学生进行活动.问:象棋与跳棋各有多少副?
小结:
此类题目的解法为:将题目中的信息对应地转化为鸡兔同笼里的三个信息:1、一只鸡、兔的腿数;2、鸡兔总头数;3、鸡兔总腿数,然后假设法去解决.
例3.灯泡厂生产灯泡的工人,按得分的多少给工资.每生产一个合格品记4分,每生产一个不合格品不仅不记分,还要扣除15分.某工人生产了1000只灯泡,共得3525分,问其中有多少个灯泡不合格?”
练习1.某次数学竞赛共20道题,评分标准是每做对一题得5分,每做错一题倒扣1分.刘亮参加了这次竞赛,得了64分.刘亮做对了多少道题?
小结:
假设法解此类题目时要理解“做对一题得5分”和“做错一题倒扣1分”之间的差距是几分,可以借助线段图理解.
三、方程法解决“鸡兔同笼”问题(选学)
例1.鸡、兔共有头100个,脚350只,鸡、兔各有多少只
练习1.鸡兔共有56只,212条腿,问鸡、兔各有几只?
小结:
列方程的等量关系式:鸡的只数2+兔的只数4=鸡兔的总脚数
例2.彩色文化用品每套19元,普通文化用品每套11元,这两种文化用品共买了16套,用钱280元.问:两种文化用品各买了多少套?
练习1.面值是2元、5元的人民币共27张,全计99元.面值是2元、5元的人民币各有多少张?
小结:
此类题目只是变换情景,方法与例1方法相同.
总结:
1.列举法:若鸡兔总头数较少时,可逐一列举;若鸡兔总头数较多时,可以先进行估算,然后跳跃列举.
2.假设法解“鸡兔同笼”问题的公式:
①假设笼子里全是鸡: 兔的只数=(实际脚数-2鸡兔的总只数)(4-2)
鸡的只数=鸡兔的总只数-兔的只数
②假设笼子里全是兔: 鸡的只数=(4鸡兔的总只数-实际脚数)(4-2)
兔的只数=鸡兔的总只数-鸡的只数
方程法:等量关系式:鸡的只数2+兔的只数4=鸡兔的总脚数
