华师大版九年级下册第27章二次函数单元测试及答案(B)
文档属性
| 名称 | 华师大版九年级下册第27章二次函数单元测试及答案(B) | 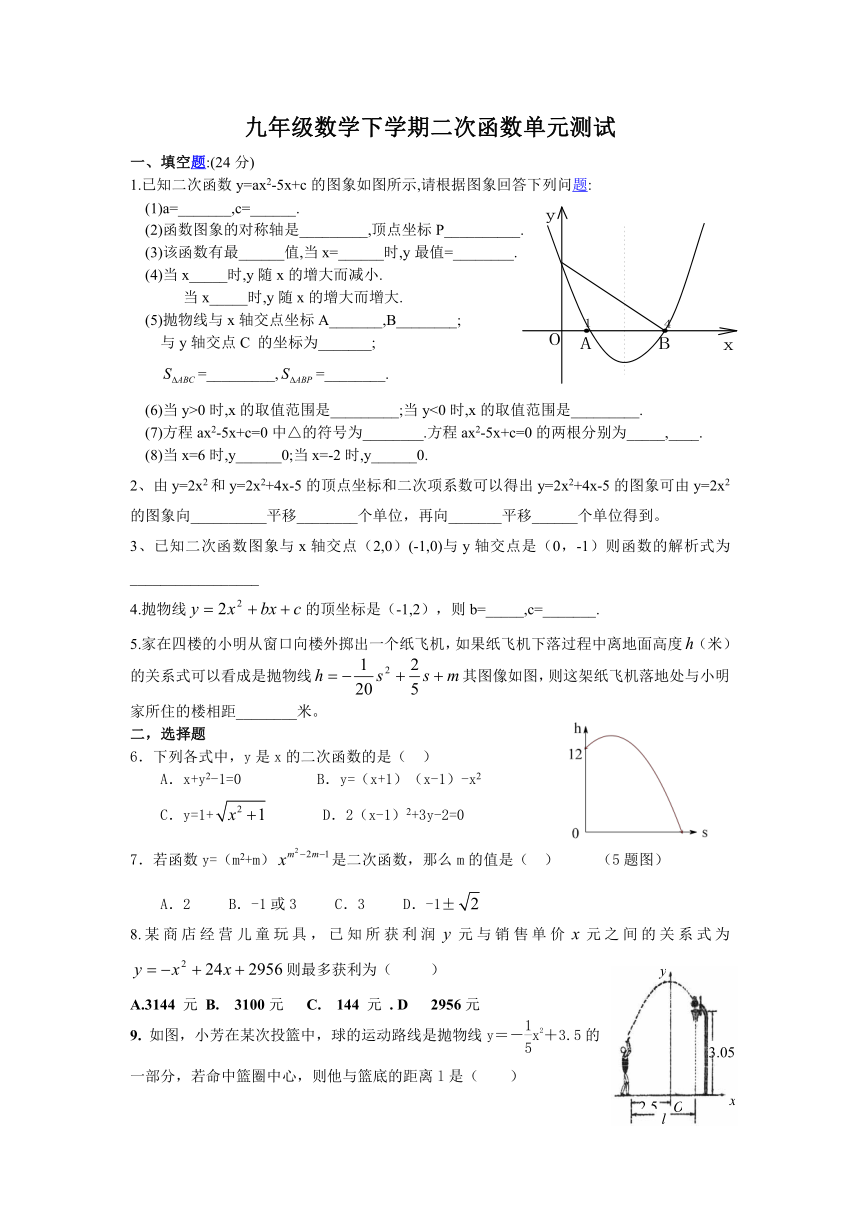 | |
| 格式 | zip | ||
| 文件大小 | 90.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-19 21:43:47 | ||
图片预览



文档简介
九年级数学下学期二次函数单元测试
一、填空题:(24分)
1.已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:
(1)a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小.
当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;
与y轴交点C 的坐标为_______;
=_________,=________.
(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
2、由y=2x2和y=2x2+4x-5的顶点坐标和二次项系数可以得出y=2x2+4x-5的图象可由y=2x2的图象向__________平移________个单位,再向_______平移______个单位得到。
3、已知二次函数图象与x轴交点(2,0)(-1,0)与y轴交点是(0,-1)则函数的解析式为_________________
4.抛物线的顶坐标是(-1,2),则b=_____,c=_______.
5.家在四楼的小明从窗口向楼外掷出一个纸飞机,如果纸飞机下落过程中离地面高度(米)的关系式可以看成是抛物线其图像如图,则这架纸飞机落地处与小明家所住的楼相距________米。
二,选择题
6.下列各式中,y是x的二次函数的是( )
A.x+y2-1=0 B.y=(x+1)(x-1)-x2
C.y=1+ D.2(x-1)2+3y-2=0
7.若函数y=(m2+m)是二次函数,那么m的值是( ) (5题图)
A.2 B.-1或3 C.3 D.-1±
8.某商店经营儿童玩具,已知所获利润元与销售单价元之间的关系式为则最多获利为( )
A.3144 元 B. 3100元 C. 144 元 . D 2956元
9. 如图,小芳在某次投篮中,球的运动路线是抛物线y=-x2+3.5的
一部分,若命中篮圈中心,则他与篮底的距离l是( )
A.3.5m B.4m C.4.5m D.4.6m
10. 物体在地球的引力作用下做自由下落运动,它的运动规律可以表示为:s=gt2.其中s 表示自某一高度下落的距离,t表示下落的时间,g是重力加速度.若某一物体从一固定高度自由下落,其运动过程中下落的距离s和时间t函数图象大致为( )
三、创新题:(每题10分,共20分)
(一)教材中的变型题
1.(教材P4第3题变题)已知二次函数y=ax2+(km+c),当x=3时,y=15;当x=-2时,y=5,试求y与x之间的函数关系式.
(二)多变题
2.如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE, 其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.
3.某化工材料经销公司购进了一批化工原料共7000千克, 购进价格为每千克30元.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现,单价定为70元时,日均销售60千克;单价每降低1元,每天多售出2千克. 在销售过程中,每天还要支出其他费用500元(天数不足一天时,按一天计算).设销售单价为x元,日均获利为y元.请你求出y关于x的二次函数关系式,并注明x的取值范围.
四、中考题:(19分)
4.(昆明,8分)某广告公司设计一幅周长为12米的矩形广告牌, 广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围.
(2)为使广告牌美观、大方,要求做成黄金矩形,请你按要求设计,并计算出可获得的设计费是多少?(精确到元)
5.影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数。有研究表明,晴天在某段公路上行驶时,速度v(km/h)的汽车的刹车距离s(m)可以由公式s=0.01v2确定;雨天行驶时,这一公式为s=0.02v2。
(1)如果汽车行驶速度是70 km/h,那么在雨天行驶和在晴天行驶相比,刹车距离相差多少米?
(2)如果汽车行驶速度分别是60 km/h与80 km/h,那么同在雨天行驶(相同的路面)相比,刹车距离相差多少?
(3)根据上述两点分析,你想对司机师傅说些什么?
6.(黄冈,11分)心理学家研究发现,一般情况下, 学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强, 中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知, 学生的注意力y随时间t的变化规律有如下关系式:
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较, 何时学生的注意力更集中?
(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
7.如图所示,有一边长为5cm的正方形ABCD和等腰三角形PQR,PQ= PR= 5cm, QR=8cm,点B、C、Q、R在同一条直线L上,当C、Q两点重合时,等腰三角形PQR以1cm/ 秒的速度沿直线L按箭头所示的方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题:
(1)当t=3时,求S的值;(2)当t=5时,求S的值;
(3)当5≤t≤8时,求S与t之间的函数关系式.
答案
一.填空:1(1)1,4 (2) (3)小 (4) (5)(1,0)
(4,0)(0,4)(6) (7)+, (8) >0 , >0
2.左,1,下,7 3. 4.. 4, 4 5. 20
二.选择:6.D 7C 8 B 9B 10B
三.1.解:把x=3,y=15;x=-2,y=5分别代入y=ax2+(xm+c),
得
解得a=2,km+c=-3, ∴y=2x2-3.
2.解:如答图,S矩形PNDM=xy,且2≤x≤4.
延长NP交EF于G,显然PG∥BF.
故,即,∴y=-x+5,
∴S=xy=-x2+5x,即S=-x2+5x(2≤x≤4).
3.解:若销售单价为x元,则每千克降低(70-x)元,日均多销售出2(70-x)千克,日均销售量为[60+2(70-x)]千克,每千克获利(x-30)元.依题意,得
y=(x-30)[60+2(70-x)]-500
=-2x2+260x-6500(30≤x≤70).
即y=-2x2+260x-6500(30≤x≤70).
四.4.解:(1)由矩形的一边长为x米,得另一边长为米,即(6-x)米,
∴S=x(6-x)=-x2+6x,即S=-x2+6x,其中0(2)设此黄金矩形的长为x米,宽为y米,
则由题意,得,解得
即当把矩形的长设计为米时,矩形将成为黄金矩形,
此时S=xy=()()=;
可获得的设计费为 ×1000≈8496(元).
5.解:(1)49米(2)56米(3)同是雨天车速越大,刹车距离越大,请司机师傅关注天气情况和控制车速。
6.解:(1)当t=5时,y=195,当t=25时,y=205.
∴讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中.
(2)当0该图的对称轴为t=12, 在对称轴左侧,y随x的增大而增大,
所以,当t=10时,y有最大值240.
当10当20故此时y<240.
所以,当t=20时,y 有最大值240.
所以,讲课开始后10分钟时,学生的注意力最集中,能持续10分钟.
(3)当0∴t=4.
当20∴t=28.57.
所以,老师可以经过适当安排,能在学生注意力达到所需的状态下讲解完这道题目.
7.解:(1)作PE⊥QR于E,
∵PQ=PR,∴QE=RE=QR=×8=4,PE==3,
当t=3时,QC=3,
设PQ 与DC相交于点G.
∵PE∥DC,∴△QCG∽△QEP,∴,
∵S△QEP=×4×3=6,∴S=(cm2)
(2)当t=5时,CR=3.
设PR与DC交于G,由△RCG∽△REP可求出S△RCG=,
∴S=S△PBR-S△RCG=12-=(cm2)
(3)当5≤t≤8时,如答图所示,QB=t-5,RC=8-t.
设PQ交AB于点H,由△QBH ∽△QEP,得S△QBH=.
设PR交CD于G,由△PCG∽△REP,得S△RCG=(8-t)2.
∴S=12--=
即关系式为S=.
一、填空题:(24分)
1.已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:
(1)a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小.
当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;
与y轴交点C 的坐标为_______;
=_________,=________.
(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
2、由y=2x2和y=2x2+4x-5的顶点坐标和二次项系数可以得出y=2x2+4x-5的图象可由y=2x2的图象向__________平移________个单位,再向_______平移______个单位得到。
3、已知二次函数图象与x轴交点(2,0)(-1,0)与y轴交点是(0,-1)则函数的解析式为_________________
4.抛物线的顶坐标是(-1,2),则b=_____,c=_______.
5.家在四楼的小明从窗口向楼外掷出一个纸飞机,如果纸飞机下落过程中离地面高度(米)的关系式可以看成是抛物线其图像如图,则这架纸飞机落地处与小明家所住的楼相距________米。
二,选择题
6.下列各式中,y是x的二次函数的是( )
A.x+y2-1=0 B.y=(x+1)(x-1)-x2
C.y=1+ D.2(x-1)2+3y-2=0
7.若函数y=(m2+m)是二次函数,那么m的值是( ) (5题图)
A.2 B.-1或3 C.3 D.-1±
8.某商店经营儿童玩具,已知所获利润元与销售单价元之间的关系式为则最多获利为( )
A.3144 元 B. 3100元 C. 144 元 . D 2956元
9. 如图,小芳在某次投篮中,球的运动路线是抛物线y=-x2+3.5的
一部分,若命中篮圈中心,则他与篮底的距离l是( )
A.3.5m B.4m C.4.5m D.4.6m
10. 物体在地球的引力作用下做自由下落运动,它的运动规律可以表示为:s=gt2.其中s 表示自某一高度下落的距离,t表示下落的时间,g是重力加速度.若某一物体从一固定高度自由下落,其运动过程中下落的距离s和时间t函数图象大致为( )
三、创新题:(每题10分,共20分)
(一)教材中的变型题
1.(教材P4第3题变题)已知二次函数y=ax2+(km+c),当x=3时,y=15;当x=-2时,y=5,试求y与x之间的函数关系式.
(二)多变题
2.如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE, 其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.
3.某化工材料经销公司购进了一批化工原料共7000千克, 购进价格为每千克30元.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现,单价定为70元时,日均销售60千克;单价每降低1元,每天多售出2千克. 在销售过程中,每天还要支出其他费用500元(天数不足一天时,按一天计算).设销售单价为x元,日均获利为y元.请你求出y关于x的二次函数关系式,并注明x的取值范围.
四、中考题:(19分)
4.(昆明,8分)某广告公司设计一幅周长为12米的矩形广告牌, 广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围.
(2)为使广告牌美观、大方,要求做成黄金矩形,请你按要求设计,并计算出可获得的设计费是多少?(精确到元)
5.影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数。有研究表明,晴天在某段公路上行驶时,速度v(km/h)的汽车的刹车距离s(m)可以由公式s=0.01v2确定;雨天行驶时,这一公式为s=0.02v2。
(1)如果汽车行驶速度是70 km/h,那么在雨天行驶和在晴天行驶相比,刹车距离相差多少米?
(2)如果汽车行驶速度分别是60 km/h与80 km/h,那么同在雨天行驶(相同的路面)相比,刹车距离相差多少?
(3)根据上述两点分析,你想对司机师傅说些什么?
6.(黄冈,11分)心理学家研究发现,一般情况下, 学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强, 中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知, 学生的注意力y随时间t的变化规律有如下关系式:
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较, 何时学生的注意力更集中?
(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
7.如图所示,有一边长为5cm的正方形ABCD和等腰三角形PQR,PQ= PR= 5cm, QR=8cm,点B、C、Q、R在同一条直线L上,当C、Q两点重合时,等腰三角形PQR以1cm/ 秒的速度沿直线L按箭头所示的方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题:
(1)当t=3时,求S的值;(2)当t=5时,求S的值;
(3)当5≤t≤8时,求S与t之间的函数关系式.
答案
一.填空:1(1)1,4 (2) (3)小 (4) (5)(1,0)
(4,0)(0,4)(6) (7)+, (8) >0 , >0
2.左,1,下,7 3. 4.. 4, 4 5. 20
二.选择:6.D 7C 8 B 9B 10B
三.1.解:把x=3,y=15;x=-2,y=5分别代入y=ax2+(xm+c),
得
解得a=2,km+c=-3, ∴y=2x2-3.
2.解:如答图,S矩形PNDM=xy,且2≤x≤4.
延长NP交EF于G,显然PG∥BF.
故,即,∴y=-x+5,
∴S=xy=-x2+5x,即S=-x2+5x(2≤x≤4).
3.解:若销售单价为x元,则每千克降低(70-x)元,日均多销售出2(70-x)千克,日均销售量为[60+2(70-x)]千克,每千克获利(x-30)元.依题意,得
y=(x-30)[60+2(70-x)]-500
=-2x2+260x-6500(30≤x≤70).
即y=-2x2+260x-6500(30≤x≤70).
四.4.解:(1)由矩形的一边长为x米,得另一边长为米,即(6-x)米,
∴S=x(6-x)=-x2+6x,即S=-x2+6x,其中0
则由题意,得,解得
即当把矩形的长设计为米时,矩形将成为黄金矩形,
此时S=xy=()()=;
可获得的设计费为 ×1000≈8496(元).
5.解:(1)49米(2)56米(3)同是雨天车速越大,刹车距离越大,请司机师傅关注天气情况和控制车速。
6.解:(1)当t=5时,y=195,当t=25时,y=205.
∴讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中.
(2)当0
所以,当t=10时,y有最大值240.
当10
所以,当t=20时,y 有最大值240.
所以,讲课开始后10分钟时,学生的注意力最集中,能持续10分钟.
(3)当0
当20
所以,老师可以经过适当安排,能在学生注意力达到所需的状态下讲解完这道题目.
7.解:(1)作PE⊥QR于E,
∵PQ=PR,∴QE=RE=QR=×8=4,PE==3,
当t=3时,QC=3,
设PQ 与DC相交于点G.
∵PE∥DC,∴△QCG∽△QEP,∴,
∵S△QEP=×4×3=6,∴S=(cm2)
(2)当t=5时,CR=3.
设PR与DC交于G,由△RCG∽△REP可求出S△RCG=,
∴S=S△PBR-S△RCG=12-=(cm2)
(3)当5≤t≤8时,如答图所示,QB=t-5,RC=8-t.
设PQ交AB于点H,由△QBH ∽△QEP,得S△QBH=.
设PR交CD于G,由△PCG∽△REP,得S△RCG=(8-t)2.
∴S=12--=
即关系式为S=.
