人教版数学八年级下册18.2.1矩形性质 课件(20张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.1矩形性质 课件(20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 09:51:21 | ||
图片预览




文档简介
(共32张PPT)
A
B
C
D
特殊
一般
特殊
有一个角是直角的平行四边形叫做矩形。
矩形的定义
训练营: 试试你的身手吧,相信自己绝对能行!
(一)请用所学的知识诊断下面的语句,若正确请在括号里打“√” 若“有病”请开药方:
1.矩形是特殊的平行四边形,特殊之处就是有一个角是直角.( )
2.平行四边形是矩形. ( )
3.平行四边形具有的性质(如平行四边形的对边平行且相等;平行四边形的对角相等;平行四边形的对角线互相平分.) 矩形也具有. ( )
√
√
有一个角是直角的平行四边形是矩形
1:矩形的四个角都是直角.
2:矩形的对角线相等.
A
B
C
D
矩形的性质
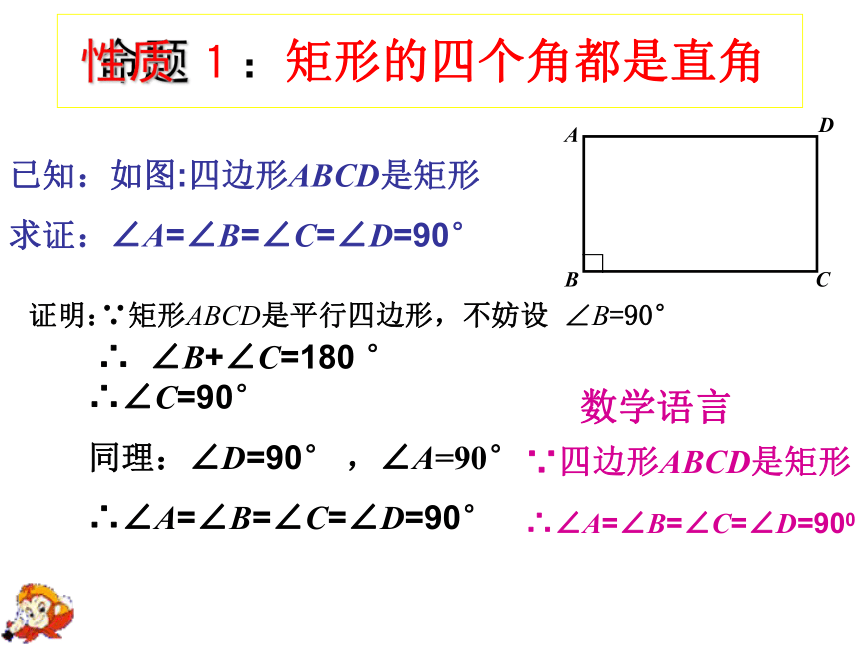
1:矩形的四个角都是直角
已知:如图:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
∴ ∠B+∠C=180 °
∴∠C=90°
同理:∠D=90° ,∠A=90°
∴∠A=∠B=∠C=∠D=90°
命题
性质
数学语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
∵矩形ABCD是平行四边形,不妨设 ∠B=90°
证明:
∟
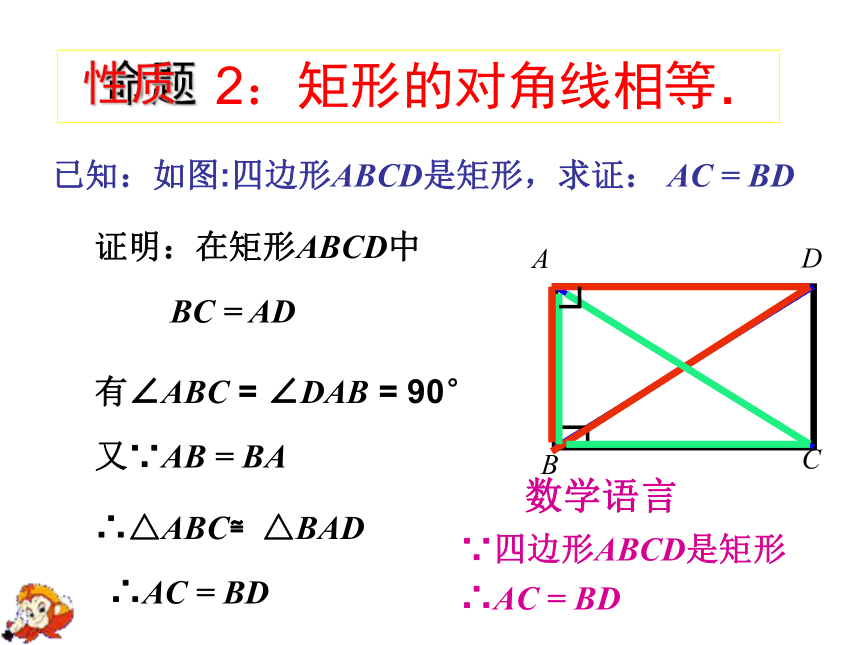
已知:如图:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明:在矩形ABCD中
BC = AD
有∠ABC = ∠DAB = 90°
又∵AB = BA
∴△ABC≌△BAD
∴AC = BD
2:矩形的对角线相等.
命题
性质
数学语言
∵四边形ABCD是矩形
∴AC = BD
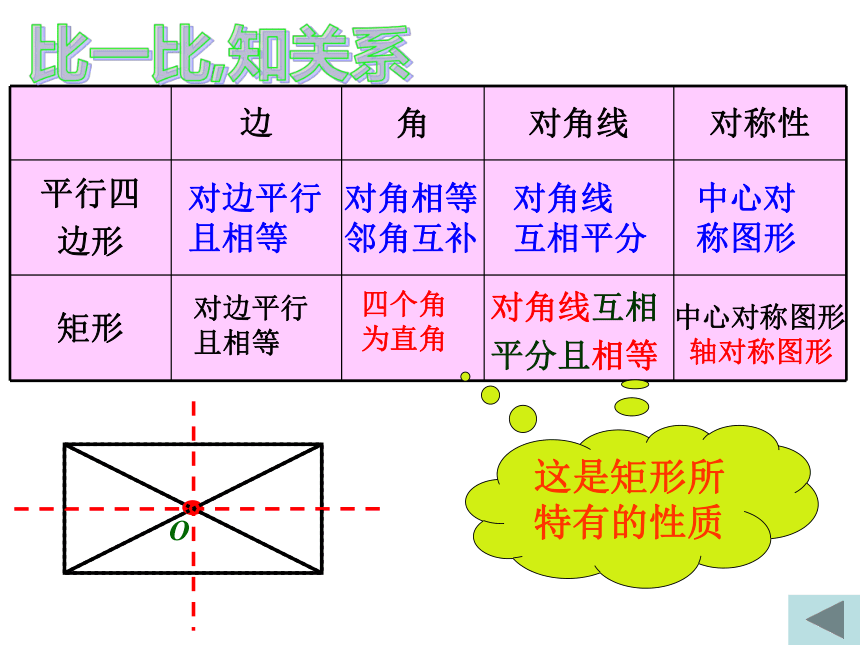
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
O
这是矩形所特有的性质
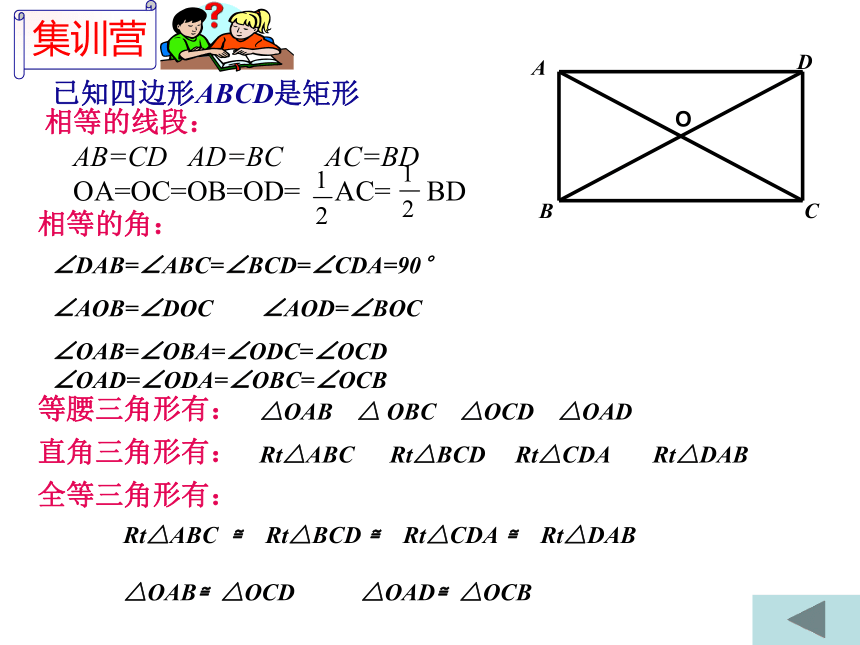
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
O
D
C
B
A
相等的线段:
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
集训营
公平,因为OA=OC=OB=OD
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
A
B
C
D
如图: 在矩形ABCD中
AO=CO=BO=DO= AC= BD
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
则有:AO= BD
推论:直角三角形的性质
直角三角形斜边上的中线等于斜边的一半。
推 导
D
C
B
A
┓
已知 如图: △ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线
若BD=3㎝,则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,∠BDC=
3 判断△ABD形状:
判断△CBD形状:
6
5
10
120°
等边三角形
等腰三角形
训练营
例: 如图,矩形ABCD的两条对角线相交于点O, AB=4㎝,求矩形对角线的长?
D
C
B
A
O
已知对角线长是8cm,两对角线的一个夹角∠AOD是120°, 求矩形的宽AB与长BC的长.
变式:
小结:如果矩形两对角线的夹角是60°或120°,则其中必有等边三角形.
60°
4
∠AOB=60°,
AD = cm ,
本节课我的收获是 。
老师对数学学习建议:
乐于探究、主动参与、学会自学是你学好数学的保证;
善于把已有的知识做为获得新知的桥梁是你学好数学的关键。
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度 (B)对角相等
(C)对边平行且相等 (D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等 (B)四个角相等
(C)是轴对称图形 (D)对角线垂直
(3) 已知矩形的一条对角线与一边的夹角是40°,
则两条对角线所夹锐角的度数为 ( )
(A)50° (B)60° (C)70° (D)80°
D
第一关
D
D
第一关
如图:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝ DE= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝
O
D
C
B
A
5
50°
10
100°
40°
12
48
28
80°
第二关
E
□
4.8
第二关
已知:如图BE、CF是△ABC的两条高,M为BC的中点,分别连ME、MF
求证: (1)ME= BC (2)ME=MF
C
M
A
B
F
E
第三关
可以明智的运用知识,再现你的魅力!
1,必做题
课本:
3,预习作业:阅读: 课本
思考:矩形性质的逆命题,
并尝试证明
2,选做题:
如图 ,四边形ABCD中,∠ABC=∠ADC=90°,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。
A
B
C
D
E
F
直角三角形性质
直角三角形斜边上的中线等于斜边的一半
推论
解题指导:矩形问题 直角三角形或等腰三角形
连接对角线
转化
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
A D
B C
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA=86-2(AC+BD)
=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
O
思考题
A
B
C
D
特殊
一般
特殊
有一个角是直角的平行四边形叫做矩形。
矩形的定义
训练营: 试试你的身手吧,相信自己绝对能行!
(一)请用所学的知识诊断下面的语句,若正确请在括号里打“√” 若“有病”请开药方:
1.矩形是特殊的平行四边形,特殊之处就是有一个角是直角.( )
2.平行四边形是矩形. ( )
3.平行四边形具有的性质(如平行四边形的对边平行且相等;平行四边形的对角相等;平行四边形的对角线互相平分.) 矩形也具有. ( )
√
√
有一个角是直角的平行四边形是矩形
1:矩形的四个角都是直角.
2:矩形的对角线相等.
A
B
C
D
矩形的性质
1:矩形的四个角都是直角
已知:如图:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
∴ ∠B+∠C=180 °
∴∠C=90°
同理:∠D=90° ,∠A=90°
∴∠A=∠B=∠C=∠D=90°
命题
性质
数学语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
∵矩形ABCD是平行四边形,不妨设 ∠B=90°
证明:
∟
已知:如图:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明:在矩形ABCD中
BC = AD
有∠ABC = ∠DAB = 90°
又∵AB = BA
∴△ABC≌△BAD
∴AC = BD
2:矩形的对角线相等.
命题
性质
数学语言
∵四边形ABCD是矩形
∴AC = BD
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
O
这是矩形所特有的性质
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
O
D
C
B
A
相等的线段:
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
集训营
公平,因为OA=OC=OB=OD
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
A
B
C
D
如图: 在矩形ABCD中
AO=CO=BO=DO= AC= BD
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
则有:AO= BD
推论:直角三角形的性质
直角三角形斜边上的中线等于斜边的一半。
推 导
D
C
B
A
┓
已知 如图: △ABC是Rt△,∠ABC=Rt∠,
BD是斜边AC上的中线
若BD=3㎝,则AC= ㎝
2 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝,∠BDC=
3 判断△ABD形状:
判断△CBD形状:
6
5
10
120°
等边三角形
等腰三角形
训练营
例: 如图,矩形ABCD的两条对角线相交于点O, AB=4㎝,求矩形对角线的长?
D
C
B
A
O
已知对角线长是8cm,两对角线的一个夹角∠AOD是120°, 求矩形的宽AB与长BC的长.
变式:
小结:如果矩形两对角线的夹角是60°或120°,则其中必有等边三角形.
60°
4
∠AOB=60°,
AD = cm ,
本节课我的收获是 。
老师对数学学习建议:
乐于探究、主动参与、学会自学是你学好数学的保证;
善于把已有的知识做为获得新知的桥梁是你学好数学的关键。
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度 (B)对角相等
(C)对边平行且相等 (D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等 (B)四个角相等
(C)是轴对称图形 (D)对角线垂直
(3) 已知矩形的一条对角线与一边的夹角是40°,
则两条对角线所夹锐角的度数为 ( )
(A)50° (B)60° (C)70° (D)80°
D
第一关
D
D
第一关
如图:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝ DE= ㎝
若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝
O
D
C
B
A
5
50°
10
100°
40°
12
48
28
80°
第二关
E
□
4.8
第二关
已知:如图BE、CF是△ABC的两条高,M为BC的中点,分别连ME、MF
求证: (1)ME= BC (2)ME=MF
C
M
A
B
F
E
第三关
可以明智的运用知识,再现你的魅力!
1,必做题
课本:
3,预习作业:阅读: 课本
思考:矩形性质的逆命题,
并尝试证明
2,选做题:
如图 ,四边形ABCD中,∠ABC=∠ADC=90°,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。
A
B
C
D
E
F
直角三角形性质
直角三角形斜边上的中线等于斜边的一半
推论
解题指导:矩形问题 直角三角形或等腰三角形
连接对角线
转化
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
A D
B C
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA=86-2(AC+BD)
=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
O
思考题
