人教版数学八年级下册 18.2.3正方形课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.2.3正方形课件(共17张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 10:08:45 | ||
图片预览

文档简介
(共17张PPT)
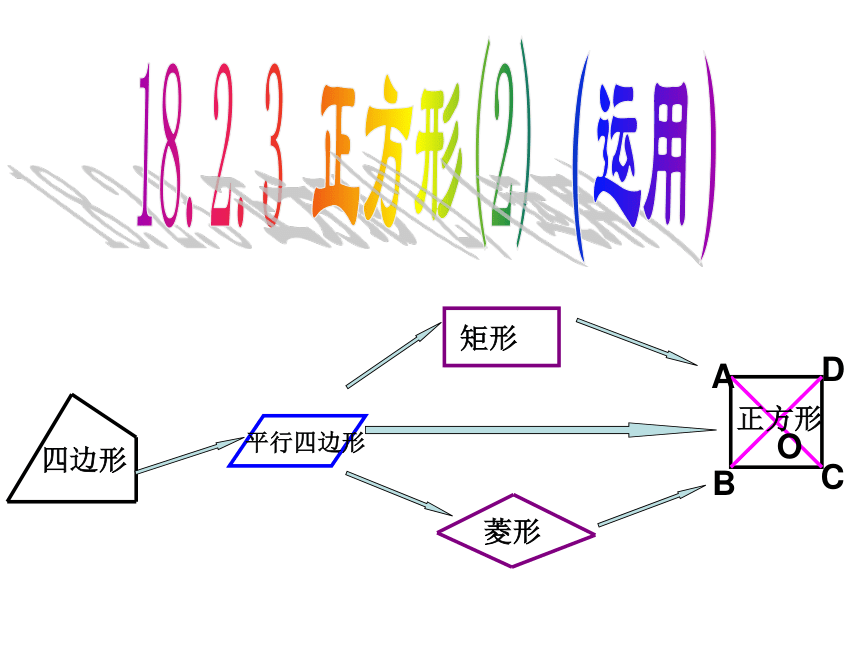
A
B
D
C
O
四边形
平行四边形
矩形
正方形
菱形
一个角是直角
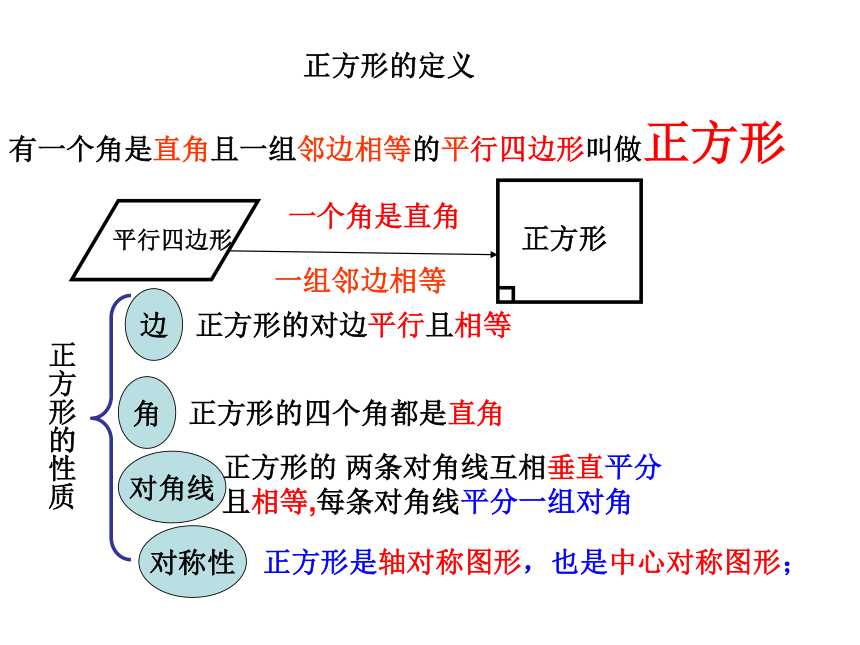
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形
平行四边形
正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
边
对角线
角
正方形的定义
正方形的性质
一组邻边相等
对称性
正方形是轴对称图形,也是中心对称图形;
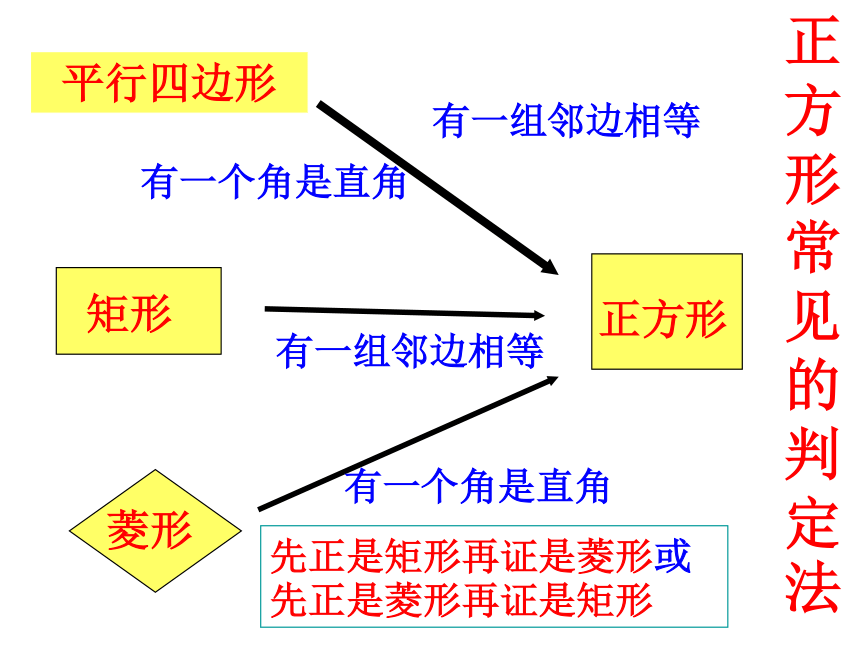
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
平行四边形
有一组邻边相等
有一个角是直角
正方形常见的判定法
先正是矩形再证是菱形或先正是菱形再证是矩形
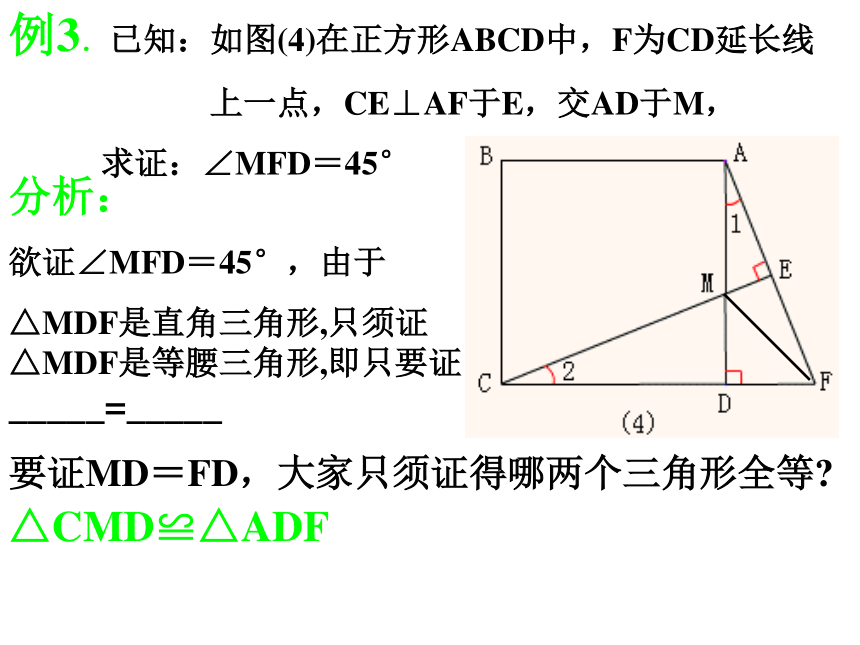
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
△CMD≌△ADF
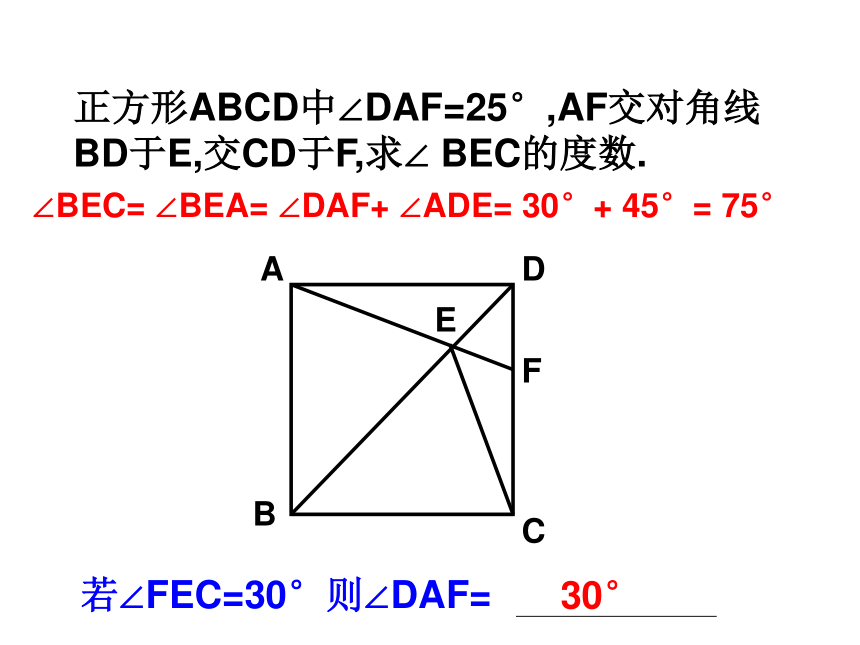
正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠ BEC的度数.
A
B
C
D
E
F
若∠FEC=30°则∠DAF=
30°
∠BEC= ∠BEA= ∠DAF+ ∠ADE= 30°+ 45°= 75°
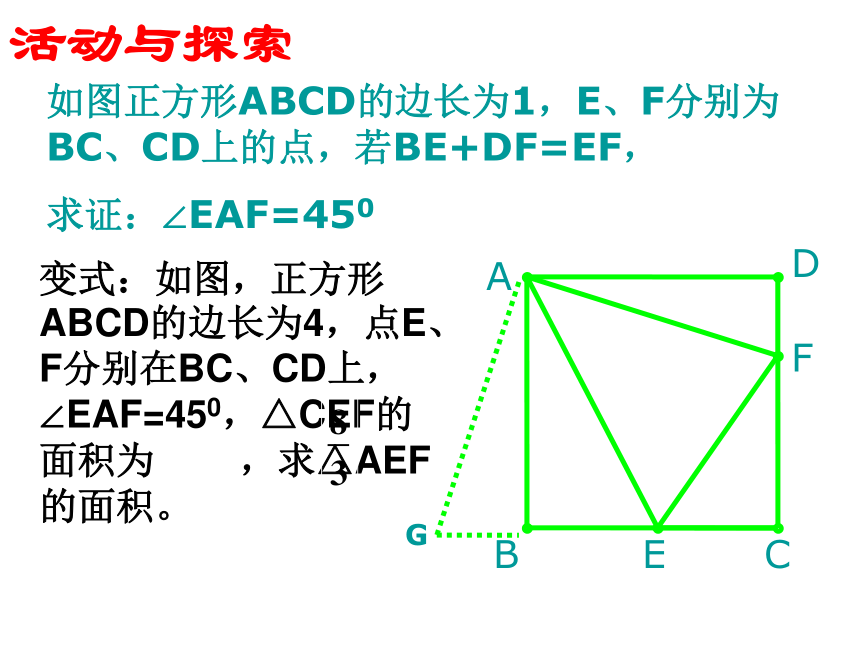
活动与探索
A
B
C
D
E
F
如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450
G
变式:如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=450,△CEF的面积为 ,求△AEF的面积。
8
3
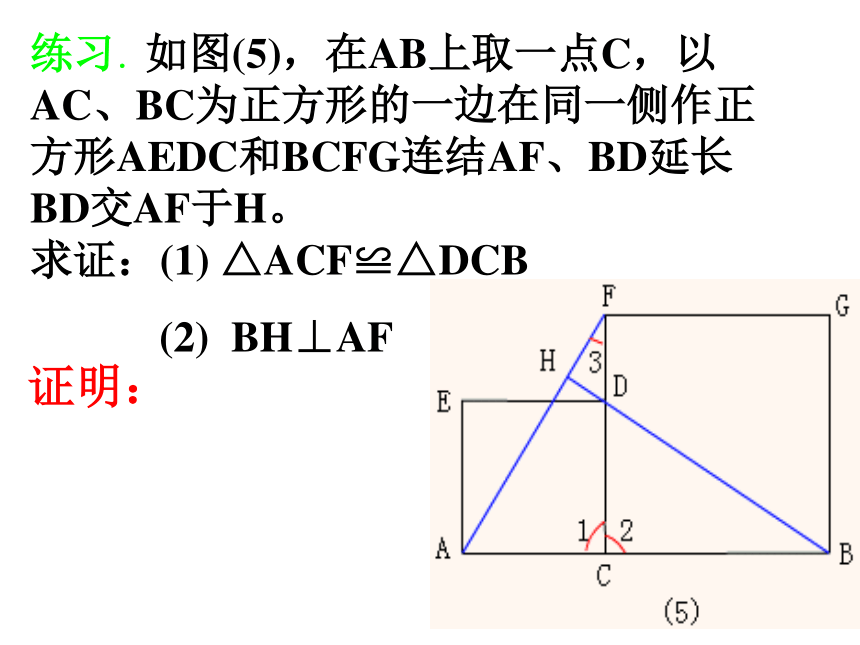
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
7
7
7
7
为什么下列三个个图形都是正方形?
5
5
5
5
5
5
5
5
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形的四边形是正方形。
两条对角线互相垂直平分且相等的四边形是正方形。
①、对角线相等的菱形是正方形
②、对角线互相垂直的矩形是正方形
③、对角线互相垂直且相等的四边
形是正方形
④ 四条边都相等的四边形是正方形
⑤、四个角都相等的四边形是正方形
⑥、四边相等,有一个角是直角的四
边形是正方形.
( )
( )
( )
( )
( )
( )
判断下列命题哪些是真命题、哪些是假命题?
真
真
假
假
假
真
1、选择题: ①、下列判断中正确的是( ) A、四边相等的四边形是正方形 B、四角相等的四边形是正方形 C、对角线垂直的平行四边形是正方形 D、对角线互相垂直平分且相等的四边形是正方形
②、在四边形ABCD中O是对角线的交点,能判定这个四边形是正方形的是( ) A、AC = BD,AB∥CD,AB = CD B、AD∥BC,∠A =∠ C C、AO=BO=CO=DO,AC⊥BD D、AO=CO,BO=DO,AB=BC
(1)正方形一定是矩形。( )
(2)正方形一定是菱形。( )
(3)菱形一定是正方形。( )
(4)矩形一定是正方形。( )
(5)正方形、矩形、菱形都是平行四边形。( )
√
×
×
√
√
D
C
A
B
C
D
C/
A/
B/
D/
已知:如图点A‘ 、 B’ 、 C‘、D’分别
是正方形ABCD四条边上的点,
并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形
①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形
证题思路分析
例题欣赏
练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)
例:如图,已知Rt△ABC中,∠C=900,∠A、∠B的角平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:四边形AEDF是正方形。
D
A
B
C
E
F
M
例:如图,E、F分别在正方形ABCD的边BC、CD上,且∠EAF=450,
试说明:EF=BE+DF
A
B
C
D
E
F
G
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师
A
B
C
D
E
F
G
H
O
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
A
B
D
C
O
四边形
平行四边形
矩形
正方形
菱形
一个角是直角
有一个角是直角且一组邻边相等的平行四边形叫做正方形
正方形
平行四边形
正方形的 两条对角线互相垂直平分且相等,每条对角线平分一组对角
正方形的对边平行且相等
正方形的四个角都是直角
边
对角线
角
正方形的定义
正方形的性质
一组邻边相等
对称性
正方形是轴对称图形,也是中心对称图形;
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
平行四边形
有一组邻边相等
有一个角是直角
正方形常见的判定法
先正是矩形再证是菱形或先正是菱形再证是矩形
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
△CMD≌△ADF
正方形ABCD中∠DAF=25°,AF交对角线BD于E,交CD于F,求∠ BEC的度数.
A
B
C
D
E
F
若∠FEC=30°则∠DAF=
30°
∠BEC= ∠BEA= ∠DAF+ ∠ADE= 30°+ 45°= 75°
活动与探索
A
B
C
D
E
F
如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,若BE+DF=EF,
求证:∠EAF=450
G
变式:如图,正方形ABCD的边长为4,点E、F分别在BC、CD上,∠EAF=450,△CEF的面积为 ,求△AEF的面积。
8
3
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
7
7
7
7
为什么下列三个个图形都是正方形?
5
5
5
5
5
5
5
5
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形的四边形是正方形。
两条对角线互相垂直平分且相等的四边形是正方形。
①、对角线相等的菱形是正方形
②、对角线互相垂直的矩形是正方形
③、对角线互相垂直且相等的四边
形是正方形
④ 四条边都相等的四边形是正方形
⑤、四个角都相等的四边形是正方形
⑥、四边相等,有一个角是直角的四
边形是正方形.
( )
( )
( )
( )
( )
( )
判断下列命题哪些是真命题、哪些是假命题?
真
真
假
假
假
真
1、选择题: ①、下列判断中正确的是( ) A、四边相等的四边形是正方形 B、四角相等的四边形是正方形 C、对角线垂直的平行四边形是正方形 D、对角线互相垂直平分且相等的四边形是正方形
②、在四边形ABCD中O是对角线的交点,能判定这个四边形是正方形的是( ) A、AC = BD,AB∥CD,AB = CD B、AD∥BC,∠A =∠ C C、AO=BO=CO=DO,AC⊥BD D、AO=CO,BO=DO,AB=BC
(1)正方形一定是矩形。( )
(2)正方形一定是菱形。( )
(3)菱形一定是正方形。( )
(4)矩形一定是正方形。( )
(5)正方形、矩形、菱形都是平行四边形。( )
√
×
×
√
√
D
C
A
B
C
D
C/
A/
B/
D/
已知:如图点A‘ 、 B’ 、 C‘、D’分别
是正方形ABCD四条边上的点,
并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形
①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形
证题思路分析
例题欣赏
练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)
例:如图,已知Rt△ABC中,∠C=900,∠A、∠B的角平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:四边形AEDF是正方形。
D
A
B
C
E
F
M
例:如图,E、F分别在正方形ABCD的边BC、CD上,且∠EAF=450,
试说明:EF=BE+DF
A
B
C
D
E
F
G
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师
A
B
C
D
E
F
G
H
O
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
