4.3.用比例解决问题(课件) 数学六年级下册(共26张PPT)人教版
文档属性
| 名称 | 4.3.用比例解决问题(课件) 数学六年级下册(共26张PPT)人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 11:58:23 | ||
图片预览




文档简介
(共26张PPT)
用比例解决问题 课时1
第 4 单元 比例
3. 比例的应用
一、复习导入
判断下列每题中的两个量是不是成比例,若是,成什么比例?
1.购买苹果的单价一定,总价和数量。
成正比例
2.差一定,减数与被减数。
不成比例
3.总路程一定,时间和速度。
成反比例
4.零件总数一定,每天生产的件数和生产的天数。
成反比例
二、探索新知
李妈
张阿姨
我们家6月份用了10t
水,水费是30元。
我们家用了12t水。
张阿姨家6月份的水费是多少钱?
阅读与理解
要解决水费的问题,就要知道水的单价和用水量。
水的单价虽然不知道,但它是一定的。
李妈
张阿姨
我们家6月份用了10t水,水费是30元。
分析与解答
我先算出每吨水的价钱,再算12t水多少钱。
张阿姨家6月份的水费是多少钱?
我们家用了12t水。
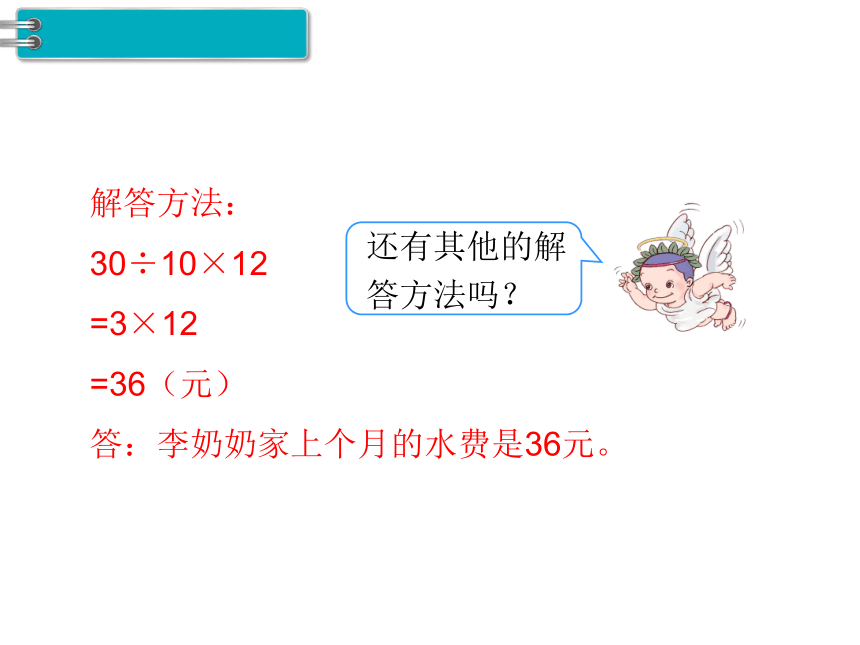
解答方法:
30÷10×12
=3×12
=36(元)
答:李奶奶家上个月的水费是36元。
还有其他的解答方法吗?
李妈
张阿姨
我们家6月份用了10t水,水费是30元。
分析与解答
可以先算出每吨水的价钱,再算12t水多少钱。
也可以用比例的方法解决!
张阿姨家6月份的水费是多少钱?
我们家用了12t水。
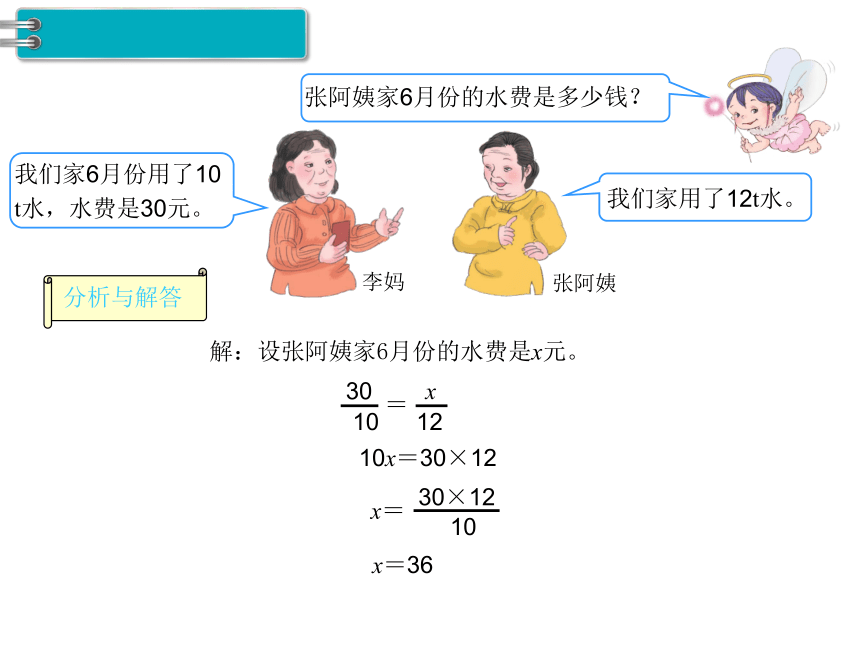
解:设张阿姨家6月份的水费是x元。
10
30
=
12
x
10x=30×12
x=
30×12
10
x=36
李妈
张阿姨
我们家6月份用了10
t水,水费是30元。
分析与解答
张阿姨家6月份的水费是多少钱?
我们家用了12t水。
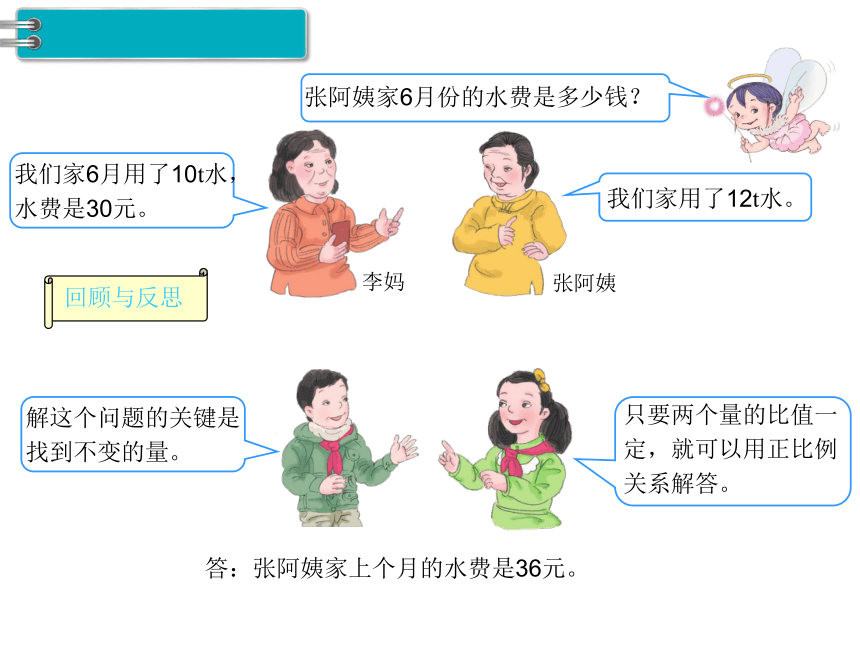
答:张阿姨家上个月的水费是36元。
回顾与反思
解这个问题的关键是找到不变的量。
只要两个量的比值一定,就可以用正比例关系解答。
李妈
张阿姨
我们家6月用了10t水,水费是30元。
张阿姨家6月份的水费是多少钱?
我们家用了12t水。
x =
10×42
30
解:设邱大爷7月用了x吨水。
30x=10×42
x = 14
答:邱大爷上个月用了14吨水。
同样的,如果邱大爷7月的水费
是42元,7月用了多少吨水?
=
10
30
x
42
三、课堂小结
解决这个问题的关键是找到不变的量,只要两个相关联量的比值一定,就可以用正比例关系解答。
四、拓展训练
1. 工程组在6天内铺设了360米长的高速公路。按照这个计算,整个项目需要12天的时间才能完成。这条公路的总长度是多少米
解:设这条公路一共长x米。
=
x=
x= 1080
答:这条公路一共长1080m。
6
360
12+6
x
6
360×18
2.小清买4支钢笔用了8元,小铭想买3支同样的钢笔,要用多少钱?
解:设要用x元。
4x=24
x=6
答:要用6元。
=
4
8
3
x
你知道哪种量不变吗?你能试着用比例解决吗?
用比例解决问题 课时2
3. 比例的应用
一、探索新知
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
阅读与理解
问题是“原来10天的用电量,现在能用几天”。
总用电量是一定的,也知道现在每天的用电量……
当总耗电量一定时,耗电量时间与单位时间耗电量成反比,即更换节能灯前后,日耗电量与耗电量天数的乘积相等。
分析与解答
因为总用电量一定,也可以用反比例关系解答。
可以先求出总用电量,再求现在的用电天数。
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
解:设原来10天的用电量现在可以用x天。
25x=100×10
x=
100×10
25
x=40
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
分析与解答
解这个问题的关键是找到哪两个量的乘积一定。
答:原来10天的用电量现在可以用40天。
只要两个量的乘积一定,就可以用反比例关系解答。
回顾与反思
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
现在30天的用电量原来只够用几天?
解:设现在30天的用电量原来只够用x天。
100x=25×30
x=7.5
答:现在30天的用电量原来只够用7.5天。
x=
25×30
100
你可以用比例解答吗?试试看吧!
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
解:设要用x元。
答:要用4.5元。
6
4
x
3
=
4x=6×3
x=
x=4.5
6×3
4
二、巩固练习
1.王明买4支圆珠笔用了6元,张刚想买3支同样的圆珠笔,
要用多少钱?
2.学校小商店有两种铅笔。小琴带的钱刚好可以买4支单
价是1.5元的,如果他只买单价是2元的,可以买多少支?
解:设可以买x支。
答:可以买3支。
2x=1.5×4
x=3
x=
1.5×4
2
3.A、B两篮子里有105个苹果,如果每个篮子里拿走3个苹果,A、B两篮子里的苹果的比例是4:5,那么这两个篮子里有多少个苹果。
解:设甲框原来有x个苹果。
(x-3):(105-x-3)=4:5
5x-15=420-4x-12
5x-15=408-4x
9x=423
x=47
105-47=58(个)
答:甲筐有47个苹果,乙筐有58个苹果。
用比例法解决问题的步骤是:
首先分析问题的意义,找出两个相关的量,判断它们是否成比例,是什么比例;
然后根据正比例或反比例的含义列出方程式;
最后解方程(解方程后测试),并写出答案。
三、课堂小结
四、课后练习
A
1.下面哪个图形是图形A按2:1放大后得到的图形?
√
只将宽度扩大到原来的2倍,高度没变。
×
×
只将高度扩大到原来的2倍,宽度没变。
B
C
D
2. 明兰身高1.5米,影子长2.5米。如果在同一时间同一地点测量一棵树的影子长度为3米,那么这棵树有多高
解:设这棵树高xm。
2.5x=3×1.5
x=1.8
答:这棵树高1.8m。
你知道吗?影长与身高的比是一个定值!试着用比例解决吧!
1.5
2.5
=
x
3
3.小明家用收割机收割小麦。如果每小时收割0.5公顷,40小时能完成任务。
解:设每小时应收割x公顷。
20x=0.5×40
x=1
答:每小时应收割1公顷。
(1)现在想用20小时收割完,那么每小时应收割多少公顷?
x=
0.5×40
20
0.5×40×8
=20×8
答:这块地共产小麦160吨。
=160(吨)
(2)每公顷产小麦8t,这块地共产小麦多少吨?
你能提出其他数学问题并解答吗?
3.小王家用收割机收割小麦。如果每小时收割0.5公顷,40小时能完成任务。
用比例解决问题 课时1
第 4 单元 比例
3. 比例的应用
一、复习导入
判断下列每题中的两个量是不是成比例,若是,成什么比例?
1.购买苹果的单价一定,总价和数量。
成正比例
2.差一定,减数与被减数。
不成比例
3.总路程一定,时间和速度。
成反比例
4.零件总数一定,每天生产的件数和生产的天数。
成反比例
二、探索新知
李妈
张阿姨
我们家6月份用了10t
水,水费是30元。
我们家用了12t水。
张阿姨家6月份的水费是多少钱?
阅读与理解
要解决水费的问题,就要知道水的单价和用水量。
水的单价虽然不知道,但它是一定的。
李妈
张阿姨
我们家6月份用了10t水,水费是30元。
分析与解答
我先算出每吨水的价钱,再算12t水多少钱。
张阿姨家6月份的水费是多少钱?
我们家用了12t水。
解答方法:
30÷10×12
=3×12
=36(元)
答:李奶奶家上个月的水费是36元。
还有其他的解答方法吗?
李妈
张阿姨
我们家6月份用了10t水,水费是30元。
分析与解答
可以先算出每吨水的价钱,再算12t水多少钱。
也可以用比例的方法解决!
张阿姨家6月份的水费是多少钱?
我们家用了12t水。
解:设张阿姨家6月份的水费是x元。
10
30
=
12
x
10x=30×12
x=
30×12
10
x=36
李妈
张阿姨
我们家6月份用了10
t水,水费是30元。
分析与解答
张阿姨家6月份的水费是多少钱?
我们家用了12t水。
答:张阿姨家上个月的水费是36元。
回顾与反思
解这个问题的关键是找到不变的量。
只要两个量的比值一定,就可以用正比例关系解答。
李妈
张阿姨
我们家6月用了10t水,水费是30元。
张阿姨家6月份的水费是多少钱?
我们家用了12t水。
x =
10×42
30
解:设邱大爷7月用了x吨水。
30x=10×42
x = 14
答:邱大爷上个月用了14吨水。
同样的,如果邱大爷7月的水费
是42元,7月用了多少吨水?
=
10
30
x
42
三、课堂小结
解决这个问题的关键是找到不变的量,只要两个相关联量的比值一定,就可以用正比例关系解答。
四、拓展训练
1. 工程组在6天内铺设了360米长的高速公路。按照这个计算,整个项目需要12天的时间才能完成。这条公路的总长度是多少米
解:设这条公路一共长x米。
=
x=
x= 1080
答:这条公路一共长1080m。
6
360
12+6
x
6
360×18
2.小清买4支钢笔用了8元,小铭想买3支同样的钢笔,要用多少钱?
解:设要用x元。
4x=24
x=6
答:要用6元。
=
4
8
3
x
你知道哪种量不变吗?你能试着用比例解决吗?
用比例解决问题 课时2
3. 比例的应用
一、探索新知
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
阅读与理解
问题是“原来10天的用电量,现在能用几天”。
总用电量是一定的,也知道现在每天的用电量……
当总耗电量一定时,耗电量时间与单位时间耗电量成反比,即更换节能灯前后,日耗电量与耗电量天数的乘积相等。
分析与解答
因为总用电量一定,也可以用反比例关系解答。
可以先求出总用电量,再求现在的用电天数。
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
解:设原来10天的用电量现在可以用x天。
25x=100×10
x=
100×10
25
x=40
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
分析与解答
解这个问题的关键是找到哪两个量的乘积一定。
答:原来10天的用电量现在可以用40天。
只要两个量的乘积一定,就可以用反比例关系解答。
回顾与反思
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
现在30天的用电量原来只够用几天?
解:设现在30天的用电量原来只够用x天。
100x=25×30
x=7.5
答:现在30天的用电量原来只够用7.5天。
x=
25×30
100
你可以用比例解答吗?试试看吧!
一座办公大楼每天平均使用100千瓦时的照明电力。改用节能灯后,平均日用电量仅25千瓦时。原来的10天耗电量现在可以用多少天
解:设要用x元。
答:要用4.5元。
6
4
x
3
=
4x=6×3
x=
x=4.5
6×3
4
二、巩固练习
1.王明买4支圆珠笔用了6元,张刚想买3支同样的圆珠笔,
要用多少钱?
2.学校小商店有两种铅笔。小琴带的钱刚好可以买4支单
价是1.5元的,如果他只买单价是2元的,可以买多少支?
解:设可以买x支。
答:可以买3支。
2x=1.5×4
x=3
x=
1.5×4
2
3.A、B两篮子里有105个苹果,如果每个篮子里拿走3个苹果,A、B两篮子里的苹果的比例是4:5,那么这两个篮子里有多少个苹果。
解:设甲框原来有x个苹果。
(x-3):(105-x-3)=4:5
5x-15=420-4x-12
5x-15=408-4x
9x=423
x=47
105-47=58(个)
答:甲筐有47个苹果,乙筐有58个苹果。
用比例法解决问题的步骤是:
首先分析问题的意义,找出两个相关的量,判断它们是否成比例,是什么比例;
然后根据正比例或反比例的含义列出方程式;
最后解方程(解方程后测试),并写出答案。
三、课堂小结
四、课后练习
A
1.下面哪个图形是图形A按2:1放大后得到的图形?
√
只将宽度扩大到原来的2倍,高度没变。
×
×
只将高度扩大到原来的2倍,宽度没变。
B
C
D
2. 明兰身高1.5米,影子长2.5米。如果在同一时间同一地点测量一棵树的影子长度为3米,那么这棵树有多高
解:设这棵树高xm。
2.5x=3×1.5
x=1.8
答:这棵树高1.8m。
你知道吗?影长与身高的比是一个定值!试着用比例解决吧!
1.5
2.5
=
x
3
3.小明家用收割机收割小麦。如果每小时收割0.5公顷,40小时能完成任务。
解:设每小时应收割x公顷。
20x=0.5×40
x=1
答:每小时应收割1公顷。
(1)现在想用20小时收割完,那么每小时应收割多少公顷?
x=
0.5×40
20
0.5×40×8
=20×8
答:这块地共产小麦160吨。
=160(吨)
(2)每公顷产小麦8t,这块地共产小麦多少吨?
你能提出其他数学问题并解答吗?
3.小王家用收割机收割小麦。如果每小时收割0.5公顷,40小时能完成任务。
