2021-2022学年人教版八年级数学下册16.3 二次根式的加减 同步练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册16.3 二次根式的加减 同步练习 (word版含答案) | 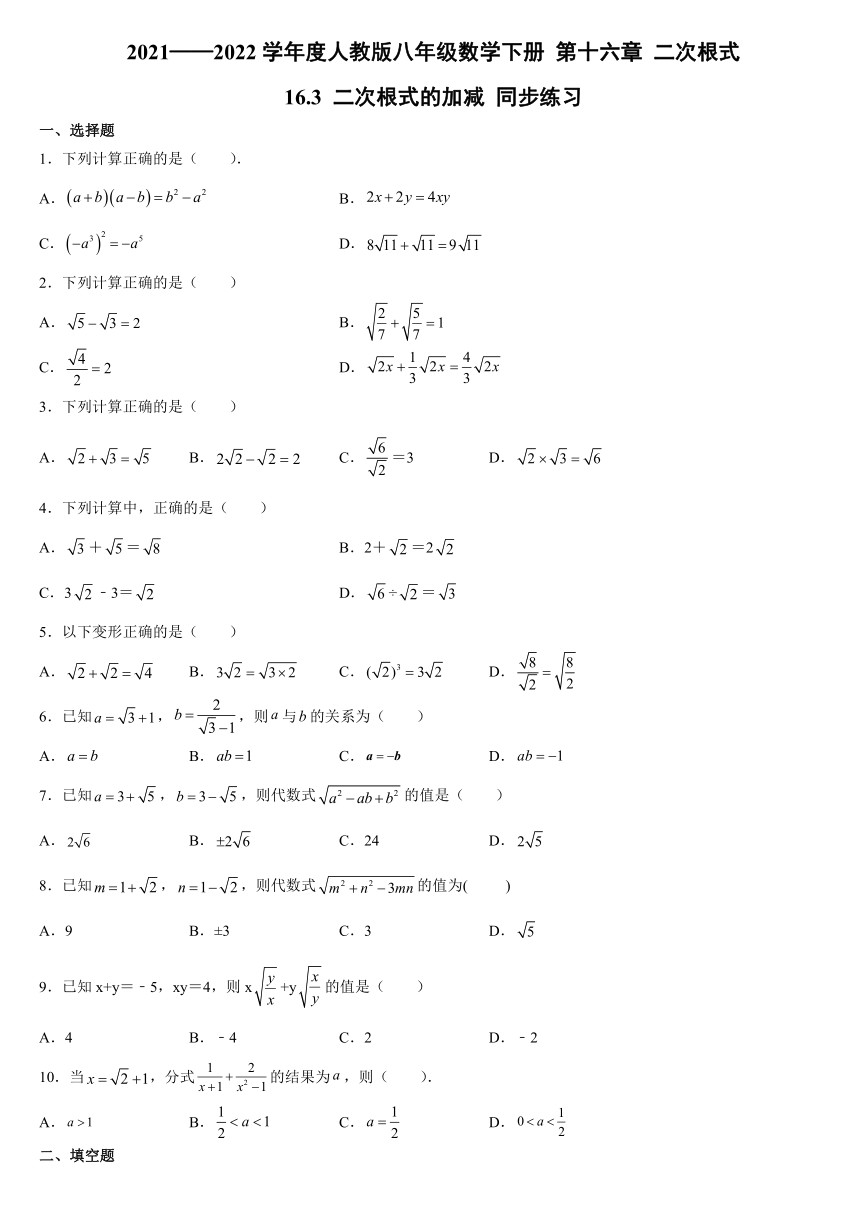 | |
| 格式 | docx | ||
| 文件大小 | 131.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 16:49:25 | ||
图片预览
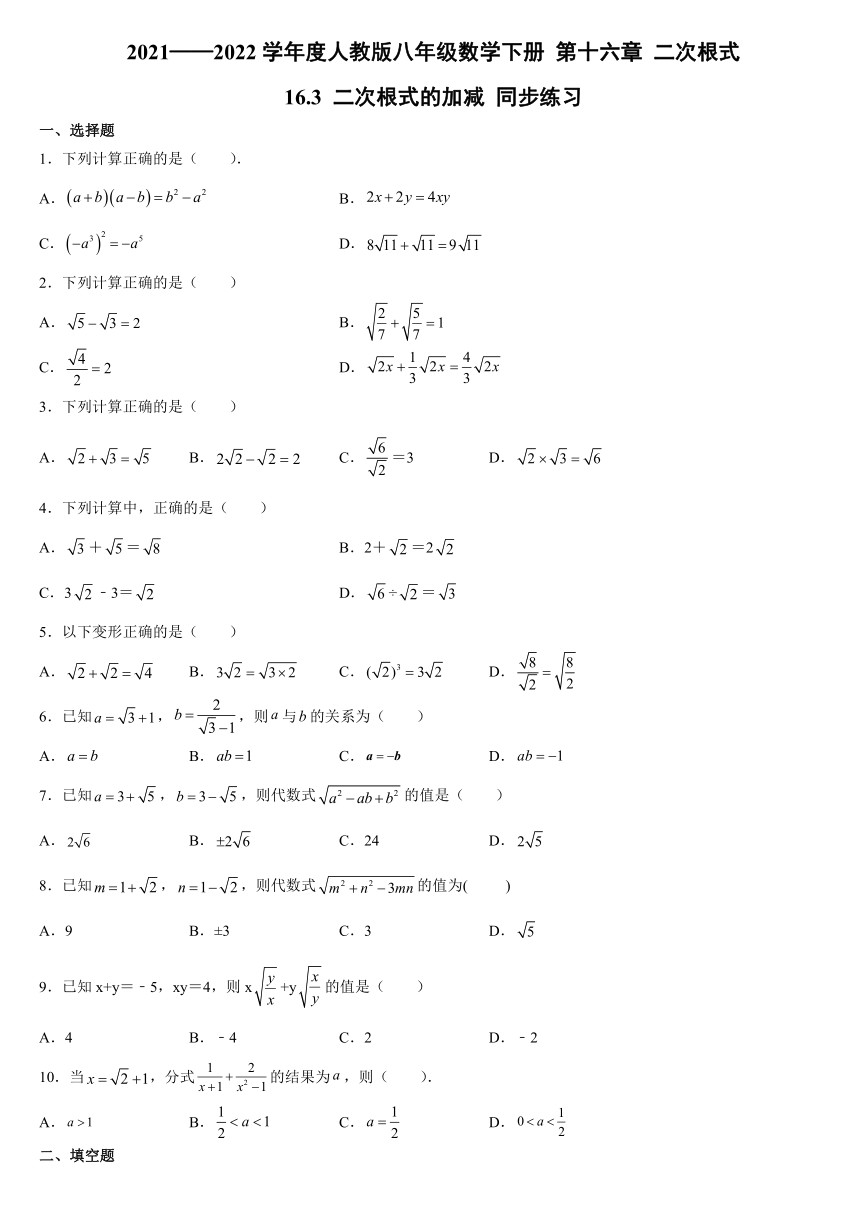

文档简介
2021——2022学年度人教版八年级数学下册 第十六章 二次根式
16.3 二次根式的加减 同步练习
一、选择题
1.下列计算正确的是( ).
A. B.
C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.下列计算正确的是( )
A. B. C.=3 D.
4.下列计算中,正确的是( )
A.+= B.2+=2
C.3﹣3= D.÷=
5.以下变形正确的是( )
A. B. C. D.
6.已知,,则与的关系为( )
A. B. C. D.
7.已知,,则代数式的值是( )
A. B. C.24 D.
8.已知,,则代数式的值为( )
A.9 B.±3 C.3 D.
9.已知x+y=﹣5,xy=4,则x+y的值是( )
A.4 B.﹣4 C.2 D.﹣2
10.当,分式的结果为,则( ).
A. B. C. D.
二、填空题
11.比较大小:3_____5.(填“>”、“=”或“<”)
12.已知,,则________.
13.计算:______.
14.规定,则的值是_________.
15.已知a=2+,b=2﹣,则的值为_________.
三、解答题
16.计算:
(1); (2);
(3); (4).
17.计算:
(1); (2);
(3); (4).
18.先化简再求值:,其中x=+2.
19.先化简再求值:() ,其中a=2+,b=2﹣.
20.(1)已知x=+2,y=﹣2,求下列各式的值:
① ;
②x2﹣xy+y2;
(2)若=8,则﹣= .
21.观察下列各式及其验证过程:,,,…
验证:;
(1)请仿照上面的方法来验证;
(2)根据上面反映的规律,请将猜到的规律用含自然数的代数式表示出来.
22.阅读材料,并回答问题:形如,的数可以化简,其化简的目的主要把原数分母中的无理数化为有理数,如,这样的化简过程叫做分母有理化.
我们把叫做的有理化因式,叫做的有理化因式.
(1)问题:的有理化因式是________,的有理化因式是________.
(2)应用:分母有理化.
(3)拓展:比较大小与.
23.先阅读下列解答过程,再解答.
(1)形如的化简,只要我们找到两个数、,使,,
即,,那么便有:.
例如:化简.
解:只要我们找到两个数、,使,,这里,,
由于,,
即,,
所以.
根据上述例题的方法化简:.
(2)小明在解决问题:已知,,求的值,他是这样分析与解答的:
.
.
,即..
.
请你根据小明的分析过程,解决如下问题:
①计算: ;
②若,求的值
【参考答案】
1.D 2.D 3.D 4.D 5.D 6.A 7.A 8.C 9.B 10.B
11.<.
12.
13.
14.
15.﹣8
16.(1)0;(2);(3);(4).
17.(1);(2);(3);(4).
18.
19.
20.(1)①;②19;(2)±.
21.(1)略;(2)
22.(1),;(2);(3)
23.(1);(2)①;②3
16.3 二次根式的加减 同步练习
一、选择题
1.下列计算正确的是( ).
A. B.
C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.下列计算正确的是( )
A. B. C.=3 D.
4.下列计算中,正确的是( )
A.+= B.2+=2
C.3﹣3= D.÷=
5.以下变形正确的是( )
A. B. C. D.
6.已知,,则与的关系为( )
A. B. C. D.
7.已知,,则代数式的值是( )
A. B. C.24 D.
8.已知,,则代数式的值为( )
A.9 B.±3 C.3 D.
9.已知x+y=﹣5,xy=4,则x+y的值是( )
A.4 B.﹣4 C.2 D.﹣2
10.当,分式的结果为,则( ).
A. B. C. D.
二、填空题
11.比较大小:3_____5.(填“>”、“=”或“<”)
12.已知,,则________.
13.计算:______.
14.规定,则的值是_________.
15.已知a=2+,b=2﹣,则的值为_________.
三、解答题
16.计算:
(1); (2);
(3); (4).
17.计算:
(1); (2);
(3); (4).
18.先化简再求值:,其中x=+2.
19.先化简再求值:() ,其中a=2+,b=2﹣.
20.(1)已知x=+2,y=﹣2,求下列各式的值:
① ;
②x2﹣xy+y2;
(2)若=8,则﹣= .
21.观察下列各式及其验证过程:,,,…
验证:;
(1)请仿照上面的方法来验证;
(2)根据上面反映的规律,请将猜到的规律用含自然数的代数式表示出来.
22.阅读材料,并回答问题:形如,的数可以化简,其化简的目的主要把原数分母中的无理数化为有理数,如,这样的化简过程叫做分母有理化.
我们把叫做的有理化因式,叫做的有理化因式.
(1)问题:的有理化因式是________,的有理化因式是________.
(2)应用:分母有理化.
(3)拓展:比较大小与.
23.先阅读下列解答过程,再解答.
(1)形如的化简,只要我们找到两个数、,使,,
即,,那么便有:.
例如:化简.
解:只要我们找到两个数、,使,,这里,,
由于,,
即,,
所以.
根据上述例题的方法化简:.
(2)小明在解决问题:已知,,求的值,他是这样分析与解答的:
.
.
,即..
.
请你根据小明的分析过程,解决如下问题:
①计算: ;
②若,求的值
【参考答案】
1.D 2.D 3.D 4.D 5.D 6.A 7.A 8.C 9.B 10.B
11.<.
12.
13.
14.
15.﹣8
16.(1)0;(2);(3);(4).
17.(1);(2);(3);(4).
18.
19.
20.(1)①;②19;(2)±.
21.(1)略;(2)
22.(1),;(2);(3)
23.(1);(2)①;②3
