人教版八年级数学 下册 第二十章 20.3 课题学习 体质健康测试中的数据分析 同步练习题(含答案)
文档属性
| 名称 | 人教版八年级数学 下册 第二十章 20.3 课题学习 体质健康测试中的数据分析 同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 66.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 15:26:59 | ||
图片预览

文档简介
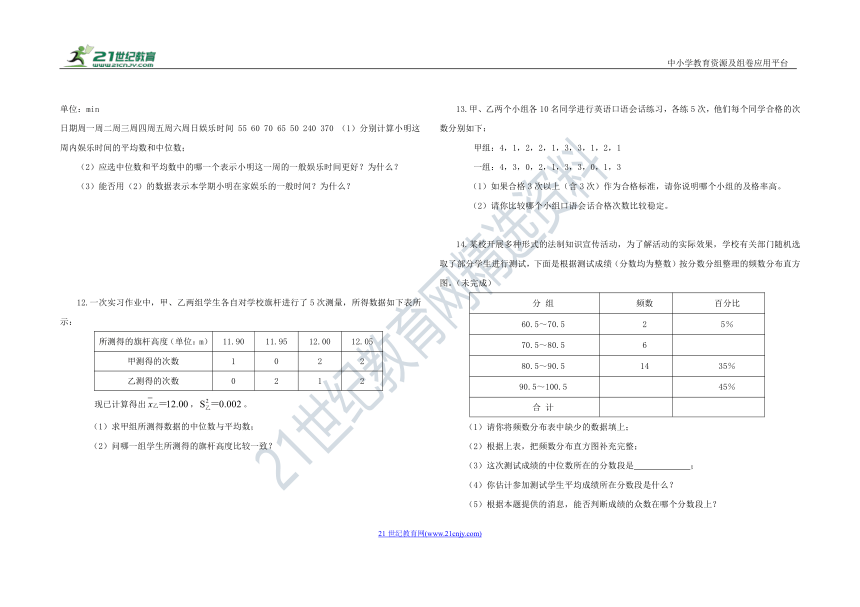
中小学教育资源及组卷应用平台
第二十章 数据的分析
20.3 体质健康测试中的数据分析
一、选择题
1.李大伯承包了一个果园,种植了100棵樱桃树,今年已进入收获期,收获时,从中任选并摘了10棵树的樱桃,分别称得每棵树所产樱桃的质量如下表:
序号 1 2 3 4 5 6 7 8 9 10 质量(千克) 14 21 27 17 18 20 19 23 19 22 据调查,市场上今年樱桃的批发价格为每千克15元,用所学的知识估计今年此果园樱桃的总产量与按批发价格销售樱桃所得的总收入分别为( ).
A.200千克,3000元 B.1900千克,28500元
C.2000千克,30000元 D.1850千克,27750元
2.班里选举班长,采用全班无记名投票的方式民主选举,选举结果主要依据是( )
A. 平均数B. 中位数C. 众数D. 方差
3.下列特征量不能反映一组数据集中趋势的是( )
A.众数 B.中位数 C.方差 D.平均数
4.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
5..期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”,上面两位同学的话能反映出的统计量是( )
A.众数和平均数 B.平均数和中位数
C.众数和方差 D.众数和中位数
填空题
6.一组学生的身高是(单位:米)1.60、1.65、1.59、1.70、1.72、1.70、1.75、1.60、1.70、1.68,则这组学生身高数据的极差是_______米
7.已知一组数据:-2,-2,3,-2,x,-1,若这组数据的平均数是0.5,则这组数据的中位数是_______,众数是_________.
8.为了估计湖里有多少鱼,我们从湖里捕上150条鱼作上标记,然后放回湖里去,经过一段时间再捕上300条鱼,其中带标记的鱼有30条,则估计湖里约有鱼_______条.
9.某"中学生暑期环保小组"的同学,随机调查了"幸福小区"10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9利用上述数据估计该小区2000户家庭一周内需要环保方便袋_______只
10.某公司欲招聘工人,对候选人进行三项测试:语言、创新、综合知识,并按测试得分1:4:3的比例确定测试总分,已知三项得分分别为88,72,50,则这位候选人的招聘得分为________.
三、解答题
11.小明的爸爸为了解小明这学期在家的作息时间,随机挑选了某个星期对小明进行了观察,并记录了他娱乐的时间:
单位:min
日期周一周二周三周四周五周六周日娱乐时间 55 60 70 65 50 240 370 (1)分别计算小明这周内娱乐时间的平均数和中位数;
(2)应选中位数和平均数中的哪一个表示小明这一周的一般娱乐时间更好?为什么?
(3)能否用(2)的数据表示本学期小明在家娱乐的一般时间?为什么?
12.一次实习作业中,甲、乙两组学生各自对学校旗杆进行了5次测量,所得数据如下表所示:
所测得的旗杆高度(单位:m) 11.90 11.95 12.00 12.05
甲测得的次数 1 0 2 2
乙测得的次数 0 2 1 2
现已计算得出,。
(1)求甲组所测得数据的中位数与平均数;
(2)问哪一组学生所测得的旗杆高度比较一致?
13.甲、乙两个小组各10名同学进行英语口语会话练习,各练5次,他们每个同学合格的次数分别如下:
甲组:4,1,2,2,1,3,3,1,2,1
一组:4,3,0,2,1,3,3,0,1,3
(1)如果合格3次以上(含3次)作为合格标准,请你说明哪个小组的及格率高。
(2)请你比较哪个小组口语会话合格次数比较稳定。
14.某校开展多种形式的法制知识宣传活动,为了解活动的实际效果,学校有关部门随机选取了部分学生进行测试,下面是根据测试成绩(分数均为整数)按分数分组整理的频数分布直方图。(未完成)
分 组 频数 百分比
60.5~70.5 2 5%
70.5~80.5 6
80.5~90.5 14 35%
90.5~100.5 45%
合 计
(1)请你将频数分布表中缺少的数据填上;
(2)根据上表,把频数分布直方图补充完整;
(3)这次测试成绩的中位数所在的分数段是 ;
(4)你估计参加测试学生平均成绩所在分数段是什么?
(5)根据本题提供的消息,能否判断成绩的众数在哪个分数段上?
15.题中给出的条形图是44位费尔兹奖得主获奖时的年龄统计图.经计算费尔兹奖得主获奖时的平均年龄是35岁.
根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时年龄的众数是多少?
(3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是多少?
16.在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图.请你用所学过的有关统计的知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.(图中的数字表示每一级台阶的高度(单位:cm).并且数据15,16,16,14,14,15的方差S甲2=,数据11,15,18,17,10,19的方差S乙2=).
17.某鞋店新近一批新款凉鞋,第一天这款凉鞋的销售情况如下表
鞋码(cm) 24 24.5 25 25.5 26 26.5 27 27.5
销售数量 16 3 5 0 1 2 4 10
于是该鞋店的经理就断定24cm和27.5cm的凉鞋很畅销,今后该多进货。
(1)你认为他的结论正确吗?请说明理由;
(2)请你为鞋店设计一个调查方案,并作出预测。
18.在八次数学测试中,甲、乙两人的成绩如下:
甲:89,93,88,91,94,90,88,87 乙:92,90,85,93,95,86,87,92
请你从下列角度比较两人成绩的情况,并说明理由:
(1)分别计算两人的极差;并说明谁的成绩变化范围大;
(2)根据平均数来判断两人的成绩谁优谁次;
(3)根据众数来判断两人的成绩谁优谁次;
(4)根据中位数来判断两人的成绩谁优谁次;
(5)根据方差来判断两人的成绩谁更稳定。
参考答案:
一、1.C 2.C 3.C 4.B 5.D
二、6.0.16
7.-2
8.1500
9.14000
10.65.75分
三、11.解:(1)平均数=(55+60+70+65+50+240+370)分=130分;
中位数=65分.
(2)应选择中位数更好.因为周六和周日的娱乐时间很长,可作为异常值,平均数受此影响较大,所以应选中位数.
(3)可以用这一中位数表示本学期小明在家娱乐的一般时间.因为这一周是随机抽取的,可以认为具有一定的代表性,所以这一周表示的娱乐时间平均水平的量──中位数,可以用来估计整个学期的娱乐时间平均水平,当然若要更好地作出估计,样本容量可以更大些.
12.(1)中位数12 (2)乙组学生所测得的旗杆高度比较一致
13.(1)甲组及格率30%,乙组及格率50%,∴乙组及格率高 (2), , 甲组口语会话合格次数比较稳定
14.(1)略 (2)略 (3)80.5~90.5 (4)80.5~90.5 (5)不能
15.解:(1)中位数为35.5岁,年龄超过中位数的有22人.
(2)众数是38岁.
(3)高于平均年龄的人数为22人,22÷44=50%.
16.(1)相同点:两段台阶路台阶高度的平均数相同.
不同点:两段台阶路台阶高度的中位数、方差和极差均不相同.
(2)甲段路走起来更舒服一些,因为它的台阶高度的方差小.
(3)每个台阶高度均为15cm(原平均数)使得方差为0.
17.(1)该鞋店的经理的结论不正确,
因为一天的统计量太少,不能代表一般情况,
所以该鞋店经理的结论不正确;
(2)将一个月这款凉鞋的销售情况作出统计表如下:
鞋码(cm) 24 24.5 25 25.5 26 26.5 27 27.5
销售数量 (一个月)
18.(1)甲的极差为:94-87=7分 乙的极差为:95-85=10
∴乙的变化范围大;
∴乙的变化范围大.89,93,88,91,94,90,88,87
乙:92,90,85,93,95,86,87,92
(2)甲的平均数为:(89+93+88+91+94+90+88+87)÷8=90,
乙的平均数为:(92+90+85+93+95+86+87+92)÷8=90,
∴两人的成绩相当;
(3)甲的众数为88,乙的众数为92,
∴从众数的角度看乙的成绩稍好;
(4)甲的中位数为:89.5,乙的中位数为91,
∴从中位数的角度看乙的成绩稍好;
(5)甲的方差为:
[(89-90)2+(93-90)2+(88-90)2+(91-90)2+(94-90)2+(90-90)2+(88-90)2+(87-90)2]=5.5
乙的方差为:
[(92-90)2+(90-90)2+(85-90)2+(93-90)2+(95-90)2+(86-90)2+(87-90)2+(92-90)2]=10.375∴甲的成绩更稳定。
21世纪教育网(www.21cnjy.com)
第二十章 数据的分析
20.3 体质健康测试中的数据分析
一、选择题
1.李大伯承包了一个果园,种植了100棵樱桃树,今年已进入收获期,收获时,从中任选并摘了10棵树的樱桃,分别称得每棵树所产樱桃的质量如下表:
序号 1 2 3 4 5 6 7 8 9 10 质量(千克) 14 21 27 17 18 20 19 23 19 22 据调查,市场上今年樱桃的批发价格为每千克15元,用所学的知识估计今年此果园樱桃的总产量与按批发价格销售樱桃所得的总收入分别为( ).
A.200千克,3000元 B.1900千克,28500元
C.2000千克,30000元 D.1850千克,27750元
2.班里选举班长,采用全班无记名投票的方式民主选举,选举结果主要依据是( )
A. 平均数B. 中位数C. 众数D. 方差
3.下列特征量不能反映一组数据集中趋势的是( )
A.众数 B.中位数 C.方差 D.平均数
4.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
5..期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”,上面两位同学的话能反映出的统计量是( )
A.众数和平均数 B.平均数和中位数
C.众数和方差 D.众数和中位数
填空题
6.一组学生的身高是(单位:米)1.60、1.65、1.59、1.70、1.72、1.70、1.75、1.60、1.70、1.68,则这组学生身高数据的极差是_______米
7.已知一组数据:-2,-2,3,-2,x,-1,若这组数据的平均数是0.5,则这组数据的中位数是_______,众数是_________.
8.为了估计湖里有多少鱼,我们从湖里捕上150条鱼作上标记,然后放回湖里去,经过一段时间再捕上300条鱼,其中带标记的鱼有30条,则估计湖里约有鱼_______条.
9.某"中学生暑期环保小组"的同学,随机调查了"幸福小区"10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9利用上述数据估计该小区2000户家庭一周内需要环保方便袋_______只
10.某公司欲招聘工人,对候选人进行三项测试:语言、创新、综合知识,并按测试得分1:4:3的比例确定测试总分,已知三项得分分别为88,72,50,则这位候选人的招聘得分为________.
三、解答题
11.小明的爸爸为了解小明这学期在家的作息时间,随机挑选了某个星期对小明进行了观察,并记录了他娱乐的时间:
单位:min
日期周一周二周三周四周五周六周日娱乐时间 55 60 70 65 50 240 370 (1)分别计算小明这周内娱乐时间的平均数和中位数;
(2)应选中位数和平均数中的哪一个表示小明这一周的一般娱乐时间更好?为什么?
(3)能否用(2)的数据表示本学期小明在家娱乐的一般时间?为什么?
12.一次实习作业中,甲、乙两组学生各自对学校旗杆进行了5次测量,所得数据如下表所示:
所测得的旗杆高度(单位:m) 11.90 11.95 12.00 12.05
甲测得的次数 1 0 2 2
乙测得的次数 0 2 1 2
现已计算得出,。
(1)求甲组所测得数据的中位数与平均数;
(2)问哪一组学生所测得的旗杆高度比较一致?
13.甲、乙两个小组各10名同学进行英语口语会话练习,各练5次,他们每个同学合格的次数分别如下:
甲组:4,1,2,2,1,3,3,1,2,1
一组:4,3,0,2,1,3,3,0,1,3
(1)如果合格3次以上(含3次)作为合格标准,请你说明哪个小组的及格率高。
(2)请你比较哪个小组口语会话合格次数比较稳定。
14.某校开展多种形式的法制知识宣传活动,为了解活动的实际效果,学校有关部门随机选取了部分学生进行测试,下面是根据测试成绩(分数均为整数)按分数分组整理的频数分布直方图。(未完成)
分 组 频数 百分比
60.5~70.5 2 5%
70.5~80.5 6
80.5~90.5 14 35%
90.5~100.5 45%
合 计
(1)请你将频数分布表中缺少的数据填上;
(2)根据上表,把频数分布直方图补充完整;
(3)这次测试成绩的中位数所在的分数段是 ;
(4)你估计参加测试学生平均成绩所在分数段是什么?
(5)根据本题提供的消息,能否判断成绩的众数在哪个分数段上?
15.题中给出的条形图是44位费尔兹奖得主获奖时的年龄统计图.经计算费尔兹奖得主获奖时的平均年龄是35岁.
根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时年龄的众数是多少?
(3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是多少?
16.在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图.请你用所学过的有关统计的知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.(图中的数字表示每一级台阶的高度(单位:cm).并且数据15,16,16,14,14,15的方差S甲2=,数据11,15,18,17,10,19的方差S乙2=).
17.某鞋店新近一批新款凉鞋,第一天这款凉鞋的销售情况如下表
鞋码(cm) 24 24.5 25 25.5 26 26.5 27 27.5
销售数量 16 3 5 0 1 2 4 10
于是该鞋店的经理就断定24cm和27.5cm的凉鞋很畅销,今后该多进货。
(1)你认为他的结论正确吗?请说明理由;
(2)请你为鞋店设计一个调查方案,并作出预测。
18.在八次数学测试中,甲、乙两人的成绩如下:
甲:89,93,88,91,94,90,88,87 乙:92,90,85,93,95,86,87,92
请你从下列角度比较两人成绩的情况,并说明理由:
(1)分别计算两人的极差;并说明谁的成绩变化范围大;
(2)根据平均数来判断两人的成绩谁优谁次;
(3)根据众数来判断两人的成绩谁优谁次;
(4)根据中位数来判断两人的成绩谁优谁次;
(5)根据方差来判断两人的成绩谁更稳定。
参考答案:
一、1.C 2.C 3.C 4.B 5.D
二、6.0.16
7.-2
8.1500
9.14000
10.65.75分
三、11.解:(1)平均数=(55+60+70+65+50+240+370)分=130分;
中位数=65分.
(2)应选择中位数更好.因为周六和周日的娱乐时间很长,可作为异常值,平均数受此影响较大,所以应选中位数.
(3)可以用这一中位数表示本学期小明在家娱乐的一般时间.因为这一周是随机抽取的,可以认为具有一定的代表性,所以这一周表示的娱乐时间平均水平的量──中位数,可以用来估计整个学期的娱乐时间平均水平,当然若要更好地作出估计,样本容量可以更大些.
12.(1)中位数12 (2)乙组学生所测得的旗杆高度比较一致
13.(1)甲组及格率30%,乙组及格率50%,∴乙组及格率高 (2), , 甲组口语会话合格次数比较稳定
14.(1)略 (2)略 (3)80.5~90.5 (4)80.5~90.5 (5)不能
15.解:(1)中位数为35.5岁,年龄超过中位数的有22人.
(2)众数是38岁.
(3)高于平均年龄的人数为22人,22÷44=50%.
16.(1)相同点:两段台阶路台阶高度的平均数相同.
不同点:两段台阶路台阶高度的中位数、方差和极差均不相同.
(2)甲段路走起来更舒服一些,因为它的台阶高度的方差小.
(3)每个台阶高度均为15cm(原平均数)使得方差为0.
17.(1)该鞋店的经理的结论不正确,
因为一天的统计量太少,不能代表一般情况,
所以该鞋店经理的结论不正确;
(2)将一个月这款凉鞋的销售情况作出统计表如下:
鞋码(cm) 24 24.5 25 25.5 26 26.5 27 27.5
销售数量 (一个月)
18.(1)甲的极差为:94-87=7分 乙的极差为:95-85=10
∴乙的变化范围大;
∴乙的变化范围大.89,93,88,91,94,90,88,87
乙:92,90,85,93,95,86,87,92
(2)甲的平均数为:(89+93+88+91+94+90+88+87)÷8=90,
乙的平均数为:(92+90+85+93+95+86+87+92)÷8=90,
∴两人的成绩相当;
(3)甲的众数为88,乙的众数为92,
∴从众数的角度看乙的成绩稍好;
(4)甲的中位数为:89.5,乙的中位数为91,
∴从中位数的角度看乙的成绩稍好;
(5)甲的方差为:
[(89-90)2+(93-90)2+(88-90)2+(91-90)2+(94-90)2+(90-90)2+(88-90)2+(87-90)2]=5.5
乙的方差为:
[(92-90)2+(90-90)2+(85-90)2+(93-90)2+(95-90)2+(86-90)2+(87-90)2+(92-90)2]=10.375∴甲的成绩更稳定。
21世纪教育网(www.21cnjy.com)
