2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质与判定同步练习题(word解析版)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的性质与判定同步练习题(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 21:56:27 | ||
图片预览




文档简介
2021-2022学年鲁教版八年级数学下册《6-2矩形的性质与判定》同步练习题(附答案)
1.下列关于矩形对角线的说法中,正确的是( )
A.对角线相互垂直 B.面积等于对角线乘积的一半
C.对角线平分一组对角 D.对角线相等
2.矩形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积为( )
A.bc﹣ab+ac+c2 B.ab﹣bc﹣ac+c2
C.a2+ab+bc﹣ac D.b2﹣bc+a2﹣ab
3.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
4.矩形两条对角线的夹角为60°,一条较短边长为5,则其对角线的长为( )
A.5 B.10 C.15 D.7.5
5.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C.2 D.4
6.如图,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为( )
A.600m2 B.551m2 C.550m2 D.500m2
7.如图,矩形ABCD中,AB=8,BC=6,E、F是AC上的三等分点,则S△BEF为( )
A.8 B.12 C.16 D.24
8.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
9.下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
10.将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的倍(木条宽度忽略不计),则这个平行四边形的最小内角为 度.
11.如图,平行四边形ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合,若△ACD的面积为4,则图中阴影部分两个三角形的面积和为 .
12.如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是 .
13.如图.在矩形ABCD中,对角线AC、BD交于点O,CE⊥BD点E,已知BE:DE=3:1,BD=2,则矩形ABCD的周长为 .
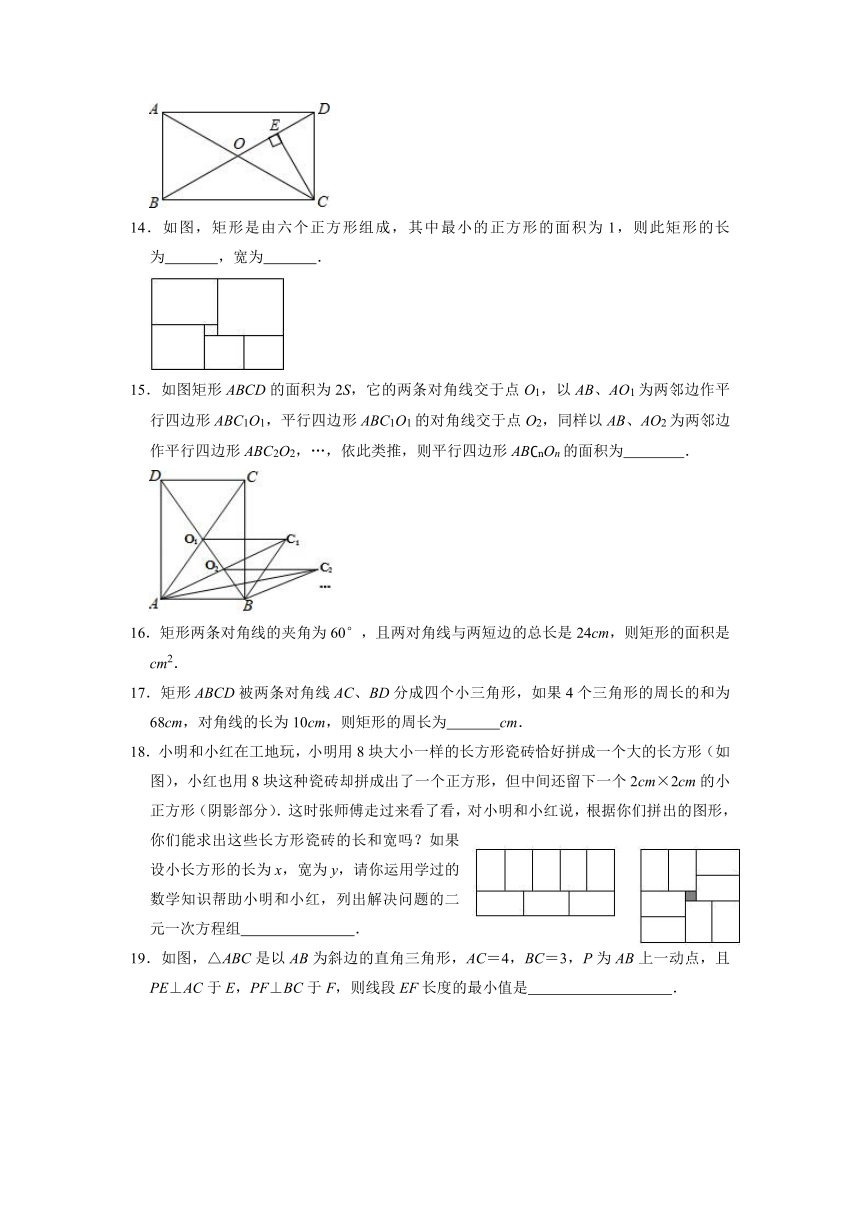
14.如图,矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的长为 ,宽为 .
15.如图矩形ABCD的面积为2S,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形AB nOn的面积为 .
16.矩形两条对角线的夹角为60°,且两对角线与两短边的总长是24cm,则矩形的面积是 cm2.
17.矩形ABCD被两条对角线AC、BD分成四个小三角形,如果4个三角形的周长的和为68cm,对角线的长为10cm,则矩形的周长为 cm.
18.小明和小红在工地玩,小明用8块大小一样的长方形瓷砖恰好拼成一个大的长方形(如图),小红也用8块这种瓷砖却拼成出了一个正方形,但中间还留下一个2cm×2cm的小正方形(阴影部分).这时张师傅走过来看了看,对小明和小红说,根据你们拼出的图形,你们能求出这些长方形瓷砖的长和宽吗?如果设小长方形的长为x,宽为y,请你运用学过的数学知识帮助小明和小红,列出解决问题的二元一次方程组 .
19.如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为AB上一动点,且PE⊥AC于E,PF⊥BC于F,则线段EF长度的最小值是 .
20.如图,已知矩形ABCD中,AE平分∠BAD交BC于点E,若∠CAE=15度,O为两条对角线的交点.求∠BOE的度数.
21.如图,在矩形ABCD中,相邻两边AB、BC分别长12cm和28cm,内角∠BAD的角平分线与边BC交于点E,连接DE.
(1)试求BE与CE的长度.
(2)△AED是不是Rt△,请说明理由.
22.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
23.如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG.
(2)当AC⊥FG时,△ABC应是怎样的三角形?为什么?
参考答案
1.解:矩形的对角线相等,
故选:D.
2.解:∵矩形ABCD的面积是ab,
阴影部分的面积是:ac+bc﹣c2,
∴图中空白部分的面积是:ab﹣(ac+bc﹣c2)=ab﹣bc﹣ac+c2.
故选:B.
3.解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12,
∵S△AOD=S△AOP+S△DOP=OA PE+OD PF=×5×PE+×5×PF=(PE+PF)=12,
解得:PE+PF=4.8.
故选:A.
4.解:如图,
矩形两条对角线的夹角为60°,可得△AOB为等边三角形,
又AB=5,所以OA=OB=5,所以对角线AC=BD=10
故选:B.
5.解:因为在矩形ABCD中,所以AO=AC=BD=BO,
又因为∠AOB=60°,所以△AOB是等边三角形,所以AO=AB=2,
所以AC=2AO=4.
故选:B.
6.解:30×20﹣30×1﹣20×1+1×1
=600﹣30﹣20+1
=551(平方米),
故选:B.
7.解:S△ABC=×8×6=24.
又E、F是AC上的三等分点.
∴S△BEF=S△ABC=8.
故选:A.
8.解:可添加AC=BD,
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形,
∴四边形ABCD是矩形,
故选:C.
9.解:A、因为对角线相等的平行四边形是矩形,所以本选项错误;
B、因为对角线互相平分且相等的四边形是矩形,所以本选项错误;
C、因为矩形的对角线相等且互相平分,所以本选项错误;
D、因为矩形的对角线相等且互相平分,所以本选项正确.
故选:D.
10.解:过点C作AB的垂线垂足是E,如图所示:
∵将四根木条钉成的矩形木框变形为平行四边形木框ABCD的形状,并使其面积为矩形木框的,
∴BC=CE,
∵sin∠CBE==,
∴∠CBE=∠A=45°.
故答案为:45.
11.解:在 ABCD中,∵△ACD的面积为4,
∴△ABC的面积为4,
∴S△ABC=AC AE=4,
∴AC AE=8,
∴矩形AEFC的面积为8,
阴影部分两个三角形的面积和=8﹣4=4,
故答案为:4.
12.解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB BC=48,OA=OC,OB=OD,AC=BD==10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12,
∵S△AOD=S△AOP+S△DOP=OA PE+OD PF=×5×PE+×5×PF=(PE+PF)=12,
解得:PE+PF=4.8.
故答案为:4.8.
13.解:在矩形ABCD中,OB=OD=OA=OC,
∵BE:DE=3:1,
∴OE=DE,
∵CE⊥OD,
∴CD=CO,
∴△OCD为等边三角形,
∵BD=2,
∴CD=,
由勾股定理得:BC==3,
∴矩形ABCD的周长为2(BC+CD)=2×(3+)=6+2.
14.解:因为,最小正方形的面积等于1,
所以,最小正方形的边长为1,
设右下角的正方形的边长为x.
所以,AB=x+1+(x+2)=2x+3,BC=2x+(x+1)=3x+1,
因为,最大正方形的边长可表示为2x﹣1,也可表示为x+3,
所以,2x﹣1=x+3,
解得:x=4,
所以,AB=11,BC=13,
故答案为:13;11.
15.解:∵DO1=BO1,DC∥O1C1∥AB,
∴夹在DC和O1C1,O1C1和AB之间的距离相等,
∴S ABC1O1=S ABCO=S,
依此类推S ABC2O2=SABC1O1=S,
…
所以第n个平行四边形的面积为S.
故答案为:S.
16.解:如图,∵四边形ABCD是矩形,
∴OA=OB=AC,
∵两条对角线的夹角为60°,
∴△ABO是等边三角形,
∵两对角线与两短边的总长是24cm,
∴AB+CD+AC+BD=AB+AB+2AB+2AB=6AB=24,
解得AB=4,
在Rt△ABD中,AD=ABtan60°=4,
所以,矩形的面积=4×4=16cm2.
故答案为:16.
17.解:∵4个三角形的周长的和为68cm,对角线的长为10cm,
∴矩形的周长=68﹣10×4=28cm.
故答案为:28.
18.解:由分析知方程组为.
19.解:连接PC.
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=∠C=90°;
又∵∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=4,BC=3,
∴AB=5,
∴AC BC=AB PC,
∴PC=.
∴线段EF长的最小值为;
故答案是:.
20.解:∵AE平分∠BAD,
∴∠BAE=∠BAD=×90°=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠BAC=45°+15°=60°,
又∵在矩形ABCD中,OA=OB,
∴△AOB是等边三角形,
∴OB=AB,∠ABO=60°,
∴OB=BE,∠OBE=90°﹣60°=30°,
∴∠BOE=(180°﹣30°)=75°.
21.解:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠DAE=∠AEB,
∵∠BAD的角平分线与边BC交于点E,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵边AB、BC分别长12cm和28cm,
∴BE=12cm,CE=BC﹣BE=28﹣12=16cm;
(2)△AED是不是Rt△,理由如下:
在Rt△ABE中,AE==12cm,
在Rt△CED中,DE===8cm,
∴AE2+DE2=288+320=608,
∵AD=BC=28cm,
∴AD2=784cm,
∴AE2+DE2=608≠AD2=784cm,
∴△AED是不是Rt△.
22.解:(1)BD=CD.
理由如下:依题意得AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD(三线合一),
∴∠ADB=90°,
∴ AFBD是矩形.
23.(1)证明:∵AD平分∠EAC,且AD∥BC,
∴∠ABC=∠EAD=∠CAD=∠ACB,
∴AB=AC;
AF是BC边上的中线,
∴AF⊥BC,
∵CG⊥AD,AD∥BC,
∴CG⊥BC,
∴AF∥CG,
∴四边形AFCG是平行四边形,
∵∠AFC=90°,
∴四边形AFCG是矩形;
∴AC=FG.
(2)解:当AC⊥FG时,△ABC是等腰直角三角形.理由如下:
∵四边形AFCG是矩形,
∴四边形AFCG是正方形,∠ACB=45°,
∵AB=AC,
∴△ABC是等腰直角三角形.
1.下列关于矩形对角线的说法中,正确的是( )
A.对角线相互垂直 B.面积等于对角线乘积的一半
C.对角线平分一组对角 D.对角线相等
2.矩形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积为( )
A.bc﹣ab+ac+c2 B.ab﹣bc﹣ac+c2
C.a2+ab+bc﹣ac D.b2﹣bc+a2﹣ab
3.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
4.矩形两条对角线的夹角为60°,一条较短边长为5,则其对角线的长为( )
A.5 B.10 C.15 D.7.5
5.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是( )
A.2 B.4 C.2 D.4
6.如图,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.根据图中数据,计算耕地的面积为( )
A.600m2 B.551m2 C.550m2 D.500m2
7.如图,矩形ABCD中,AB=8,BC=6,E、F是AC上的三等分点,则S△BEF为( )
A.8 B.12 C.16 D.24
8.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
9.下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
10.将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的倍(木条宽度忽略不计),则这个平行四边形的最小内角为 度.
11.如图,平行四边形ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合,若△ACD的面积为4,则图中阴影部分两个三角形的面积和为 .
12.如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是 .
13.如图.在矩形ABCD中,对角线AC、BD交于点O,CE⊥BD点E,已知BE:DE=3:1,BD=2,则矩形ABCD的周长为 .
14.如图,矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的长为 ,宽为 .
15.如图矩形ABCD的面积为2S,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形AB nOn的面积为 .
16.矩形两条对角线的夹角为60°,且两对角线与两短边的总长是24cm,则矩形的面积是 cm2.
17.矩形ABCD被两条对角线AC、BD分成四个小三角形,如果4个三角形的周长的和为68cm,对角线的长为10cm,则矩形的周长为 cm.
18.小明和小红在工地玩,小明用8块大小一样的长方形瓷砖恰好拼成一个大的长方形(如图),小红也用8块这种瓷砖却拼成出了一个正方形,但中间还留下一个2cm×2cm的小正方形(阴影部分).这时张师傅走过来看了看,对小明和小红说,根据你们拼出的图形,你们能求出这些长方形瓷砖的长和宽吗?如果设小长方形的长为x,宽为y,请你运用学过的数学知识帮助小明和小红,列出解决问题的二元一次方程组 .
19.如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为AB上一动点,且PE⊥AC于E,PF⊥BC于F,则线段EF长度的最小值是 .
20.如图,已知矩形ABCD中,AE平分∠BAD交BC于点E,若∠CAE=15度,O为两条对角线的交点.求∠BOE的度数.
21.如图,在矩形ABCD中,相邻两边AB、BC分别长12cm和28cm,内角∠BAD的角平分线与边BC交于点E,连接DE.
(1)试求BE与CE的长度.
(2)△AED是不是Rt△,请说明理由.
22.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
23.如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG.
(2)当AC⊥FG时,△ABC应是怎样的三角形?为什么?
参考答案
1.解:矩形的对角线相等,
故选:D.
2.解:∵矩形ABCD的面积是ab,
阴影部分的面积是:ac+bc﹣c2,
∴图中空白部分的面积是:ab﹣(ac+bc﹣c2)=ab﹣bc﹣ac+c2.
故选:B.
3.解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12,
∵S△AOD=S△AOP+S△DOP=OA PE+OD PF=×5×PE+×5×PF=(PE+PF)=12,
解得:PE+PF=4.8.
故选:A.
4.解:如图,
矩形两条对角线的夹角为60°,可得△AOB为等边三角形,
又AB=5,所以OA=OB=5,所以对角线AC=BD=10
故选:B.
5.解:因为在矩形ABCD中,所以AO=AC=BD=BO,
又因为∠AOB=60°,所以△AOB是等边三角形,所以AO=AB=2,
所以AC=2AO=4.
故选:B.
6.解:30×20﹣30×1﹣20×1+1×1
=600﹣30﹣20+1
=551(平方米),
故选:B.
7.解:S△ABC=×8×6=24.
又E、F是AC上的三等分点.
∴S△BEF=S△ABC=8.
故选:A.
8.解:可添加AC=BD,
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形,
∴四边形ABCD是矩形,
故选:C.
9.解:A、因为对角线相等的平行四边形是矩形,所以本选项错误;
B、因为对角线互相平分且相等的四边形是矩形,所以本选项错误;
C、因为矩形的对角线相等且互相平分,所以本选项错误;
D、因为矩形的对角线相等且互相平分,所以本选项正确.
故选:D.
10.解:过点C作AB的垂线垂足是E,如图所示:
∵将四根木条钉成的矩形木框变形为平行四边形木框ABCD的形状,并使其面积为矩形木框的,
∴BC=CE,
∵sin∠CBE==,
∴∠CBE=∠A=45°.
故答案为:45.
11.解:在 ABCD中,∵△ACD的面积为4,
∴△ABC的面积为4,
∴S△ABC=AC AE=4,
∴AC AE=8,
∴矩形AEFC的面积为8,
阴影部分两个三角形的面积和=8﹣4=4,
故答案为:4.
12.解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB BC=48,OA=OC,OB=OD,AC=BD==10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12,
∵S△AOD=S△AOP+S△DOP=OA PE+OD PF=×5×PE+×5×PF=(PE+PF)=12,
解得:PE+PF=4.8.
故答案为:4.8.
13.解:在矩形ABCD中,OB=OD=OA=OC,
∵BE:DE=3:1,
∴OE=DE,
∵CE⊥OD,
∴CD=CO,
∴△OCD为等边三角形,
∵BD=2,
∴CD=,
由勾股定理得:BC==3,
∴矩形ABCD的周长为2(BC+CD)=2×(3+)=6+2.
14.解:因为,最小正方形的面积等于1,
所以,最小正方形的边长为1,
设右下角的正方形的边长为x.
所以,AB=x+1+(x+2)=2x+3,BC=2x+(x+1)=3x+1,
因为,最大正方形的边长可表示为2x﹣1,也可表示为x+3,
所以,2x﹣1=x+3,
解得:x=4,
所以,AB=11,BC=13,
故答案为:13;11.
15.解:∵DO1=BO1,DC∥O1C1∥AB,
∴夹在DC和O1C1,O1C1和AB之间的距离相等,
∴S ABC1O1=S ABCO=S,
依此类推S ABC2O2=SABC1O1=S,
…
所以第n个平行四边形的面积为S.
故答案为:S.
16.解:如图,∵四边形ABCD是矩形,
∴OA=OB=AC,
∵两条对角线的夹角为60°,
∴△ABO是等边三角形,
∵两对角线与两短边的总长是24cm,
∴AB+CD+AC+BD=AB+AB+2AB+2AB=6AB=24,
解得AB=4,
在Rt△ABD中,AD=ABtan60°=4,
所以,矩形的面积=4×4=16cm2.
故答案为:16.
17.解:∵4个三角形的周长的和为68cm,对角线的长为10cm,
∴矩形的周长=68﹣10×4=28cm.
故答案为:28.
18.解:由分析知方程组为.
19.解:连接PC.
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=∠C=90°;
又∵∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=4,BC=3,
∴AB=5,
∴AC BC=AB PC,
∴PC=.
∴线段EF长的最小值为;
故答案是:.
20.解:∵AE平分∠BAD,
∴∠BAE=∠BAD=×90°=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠BAC=45°+15°=60°,
又∵在矩形ABCD中,OA=OB,
∴△AOB是等边三角形,
∴OB=AB,∠ABO=60°,
∴OB=BE,∠OBE=90°﹣60°=30°,
∴∠BOE=(180°﹣30°)=75°.
21.解:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠DAE=∠AEB,
∵∠BAD的角平分线与边BC交于点E,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵边AB、BC分别长12cm和28cm,
∴BE=12cm,CE=BC﹣BE=28﹣12=16cm;
(2)△AED是不是Rt△,理由如下:
在Rt△ABE中,AE==12cm,
在Rt△CED中,DE===8cm,
∴AE2+DE2=288+320=608,
∵AD=BC=28cm,
∴AD2=784cm,
∴AE2+DE2=608≠AD2=784cm,
∴△AED是不是Rt△.
22.解:(1)BD=CD.
理由如下:依题意得AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD(三线合一),
∴∠ADB=90°,
∴ AFBD是矩形.
23.(1)证明:∵AD平分∠EAC,且AD∥BC,
∴∠ABC=∠EAD=∠CAD=∠ACB,
∴AB=AC;
AF是BC边上的中线,
∴AF⊥BC,
∵CG⊥AD,AD∥BC,
∴CG⊥BC,
∴AF∥CG,
∴四边形AFCG是平行四边形,
∵∠AFC=90°,
∴四边形AFCG是矩形;
∴AC=FG.
(2)解:当AC⊥FG时,△ABC是等腰直角三角形.理由如下:
∵四边形AFCG是矩形,
∴四边形AFCG是正方形,∠ACB=45°,
∵AB=AC,
∴△ABC是等腰直角三角形.
