2021-2022学年鲁教版(五四制)八年级数学下册6.3正方形的性质与判定 同步练习题 (word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.3正方形的性质与判定 同步练习题 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 21:08:48 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》同步练习题(附答案)
1.正方形具有而矩形不具有的性质是( )
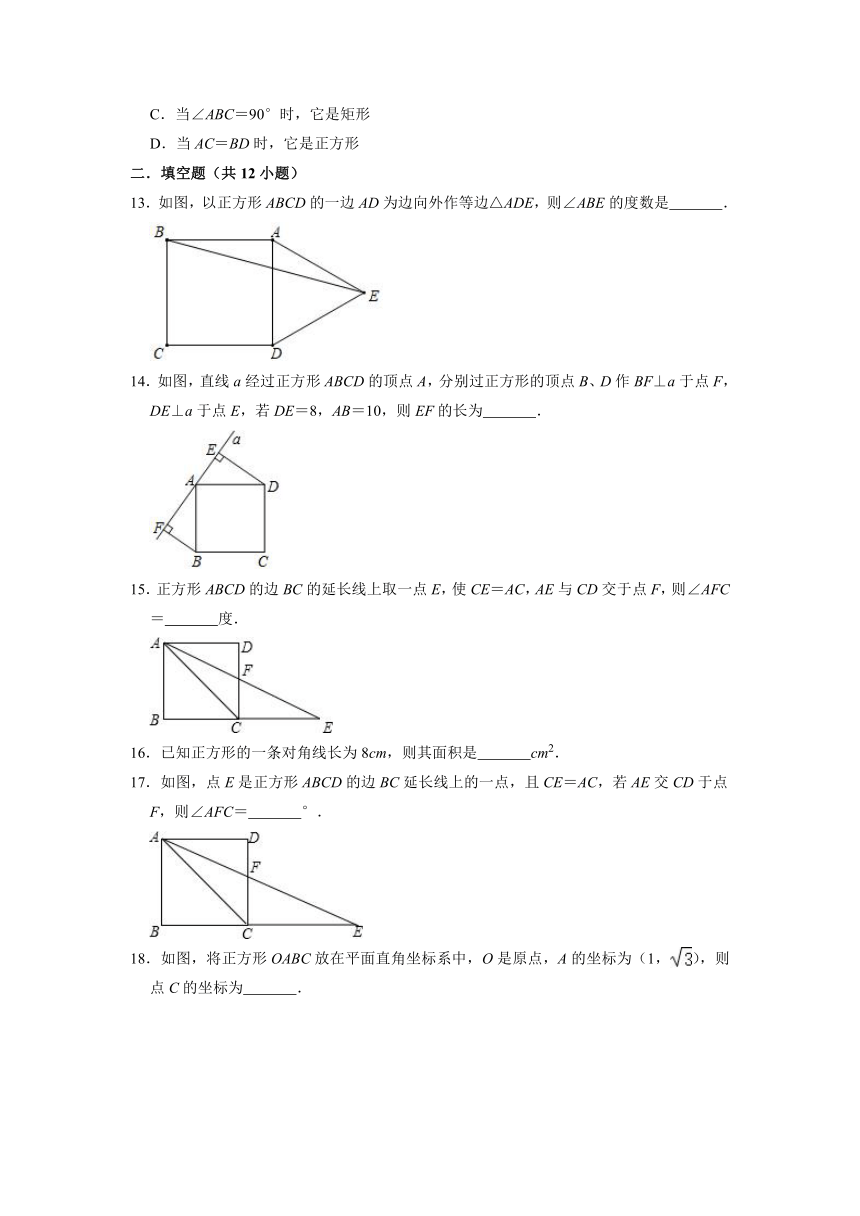
A.对角相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
2.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣3,0),B(2,b),则正方形ABCD的面积是( )
A.20 B.16 C.34 D.25
3.对角线互相垂直平分但不相等的四边形是( )
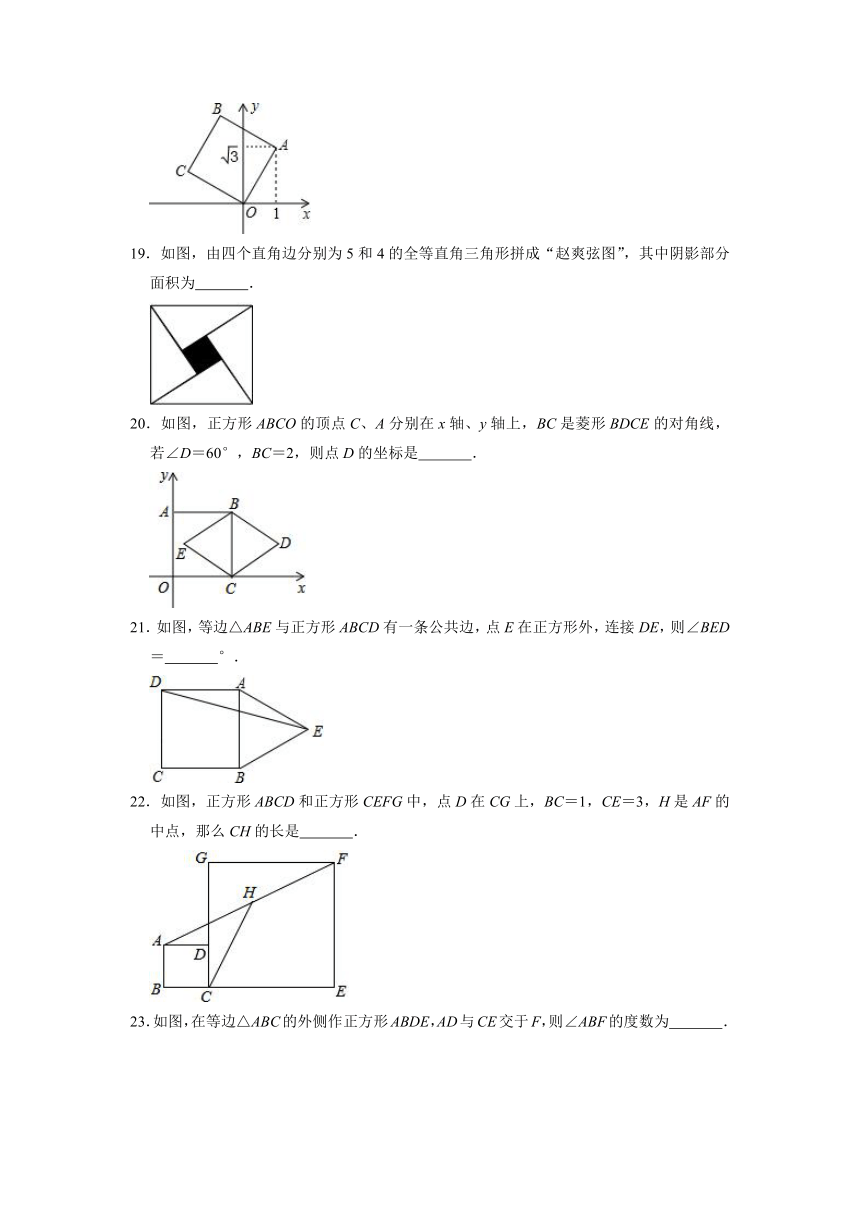
A.菱形 B.矩形 C.正方形 D.平行四边形
4.正方形具有而菱形不具备的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线平分一组对角 D.对角线相等
5.如图,将边长为2cm的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
A.() B.(2,﹣1) C.(1,) D.(﹣1,)
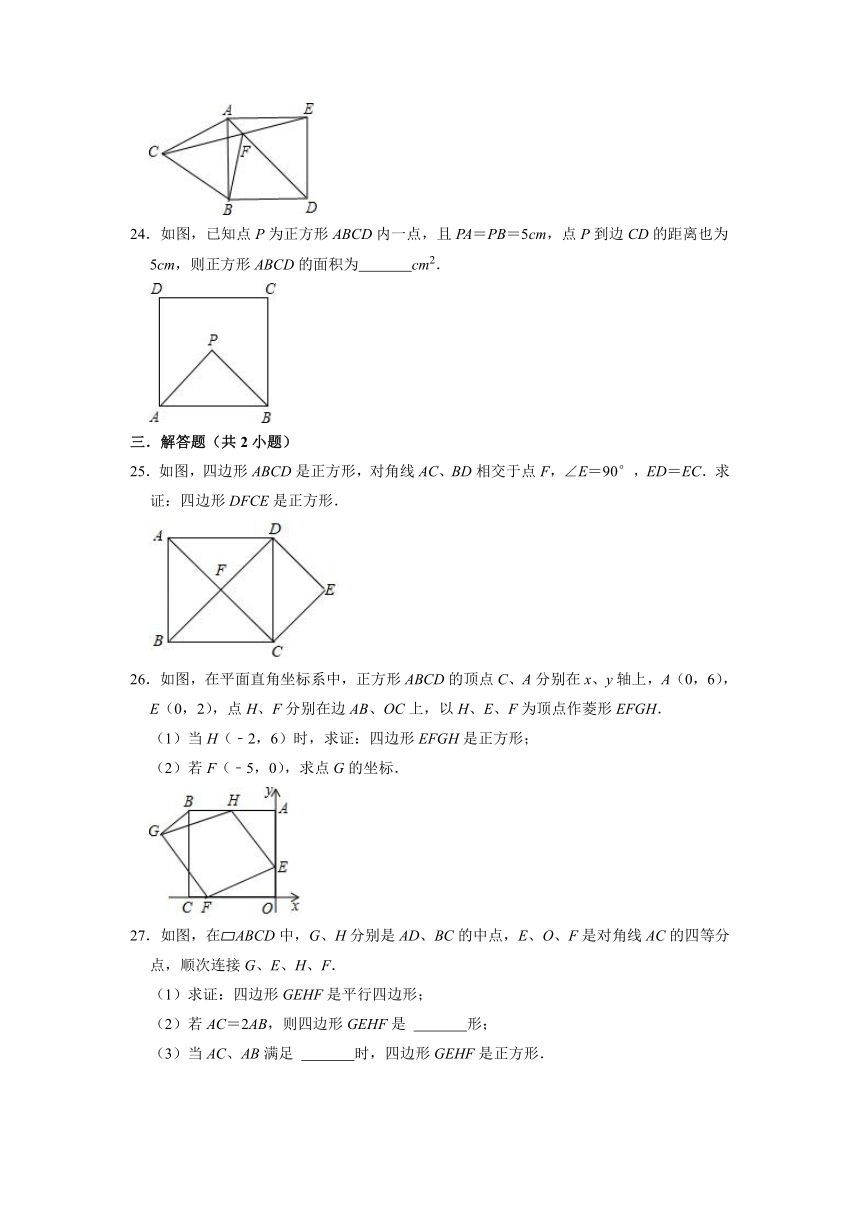
6.如图,两张对边平行且等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
7.两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
8.下列说法中,正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.矩形的对角线互相垂直
C.菱形的对角线互相垂直且平分
D.对角线互相垂直,且相等的四边形是正方形
9.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,平行四边形ABCD是菱形
B.当AC⊥BD时,平行四边形ABCD是菱形
C.当AC=BD时,平行四边形ABCD是正方形
D.当∠ABC=90°时,平行四边形ABCD是矩形
10.下列说法不正确的是( )
A.平行四边形对角相等
B.对角线互相垂直的矩形是正方形
C.一组对边相等另一组对边平行的四边形是平行四边形
D.菱形的对角线互相垂直平分
11.如图,下列四组条件中,能判定 ABCD是正方形的有( )
①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.
A.1个 B.2个 C.3个 D.4个
12.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
二.填空题(共12小题)
13.如图,以正方形ABCD的一边AD为边向外作等边△ADE,则∠ABE的度数是 .
14.如图,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,AB=10,则EF的长为 .
15.正方形ABCD的边BC的延长线上取一点E,使CE=AC,AE与CD交于点F,则∠AFC= 度.
16.已知正方形的一条对角线长为8cm,则其面积是 cm2.
17.如图,点E是正方形ABCD的边BC延长线上的一点,且CE=AC,若AE交CD于点F,则∠AFC= °.
18.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为 .
19.如图,由四个直角边分别为5和4的全等直角三角形拼成“赵爽弦图”,其中阴影部分面积为 .
20.如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是 .
21.如图,等边△ABE与正方形ABCD有一条公共边,点E在正方形外,连接DE,则∠BED= °.
22.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
23.如图,在等边△ABC的外侧作正方形ABDE,AD与CE交于F,则∠ABF的度数为 .
24.如图,已知点P为正方形ABCD内一点,且PA=PB=5cm,点P到边CD的距离也为5cm,则正方形ABCD的面积为 cm2.
三.解答题(共2小题)
25.如图,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,ED=EC.求证:四边形DFCE是正方形.
26.如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
(1)当H(﹣2,6)时,求证:四边形EFGH是正方形;
(2)若F(﹣5,0),求点G的坐标.
27.如图,在 ABCD中,G、H分别是AD、BC的中点,E、O、F是对角线AC的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)若AC=2AB,则四边形GEHF是 形;
(3)当AC、AB满足 时,四边形GEHF是正方形.
28.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,四边形BCED为平行四边形,DE、AC相交于F,连接DC、AE.
(1)试确定四边形ADCE的形状,并说明理由;
(2)若AB=8,AC=6,求四边形ADCE的面积;
(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.
参考答案
1.解:因为正方形的对角相等,对角线相等、垂直、且互相平分,矩形的对角相等,对角线相等,互相平分,
所以正方形具有而矩形不具有的性质是对角线互相垂直.
故选:D.
2.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣3,0),B(2,b),
∴OA=3,OM=2,
∴OD=AM=5,
∴AD==,
∴正方形ABCD的面积=34,
故选:C.
3.解:A、菱形的对角线互相垂直平分,且不相等,故本选项正确;
B、矩形的对角线互相平分,且相等,故本选项错误;
C、正方形的对角线互相垂直平分,且相等,故本选项错误;
D、平行四边形的对角线互相平分,故本选项错误.
故选:A.
4.解:A、对角线互相平分,正方形和菱形都具有,故本选项不符合题意;
B、对角线互相垂直,正方形和菱形都具有,故本选项不符合题意;
C、对角线平分一组对角,正方形和菱形都具有,故本选项不符合题意;
D、正方形对角线相等,菱形对角线不相等,故本选项符合题意.
故选:D.
5.解:作AD⊥y轴于D,作CE⊥y轴于E,如图所示:
则∠ADO=∠OEC=90°,
∴∠1+∠2=90°,
∵点A的坐标为(1,),
∴AD=1,OD=,
∵四边形OABC是正方形,
∴∠AOC=90°,OC=AO,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCE和△AOD中,
,
∴△OCE≌△AOD(AAS),
∴OE=AD=1,CE=OD=,
∴点C的坐标为(,﹣1).
故选:A.
6.
解:由图可知,过A点作AE⊥BC于E,AF⊥CD于F,
∵两条纸条宽度相等,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵SABCD=BC×AE=CD AF.
又∵AE=AF,
∴BC=CD,
∴四边形ABCD为菱形.
故选:B.
7.解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
8.解:A错误,如等腰梯形即为一组对边平行,另一组对边相等的四边形,却不是平行四边形;
B错误,由矩形的性质可知矩形的对角线互相平分且相等;
C正确,由菱形的性质可知菱形的对角线互相垂直且平分;
D错误,由正方形的性质及判定可知,对角线互相垂直,平分,且相等的四边形是正方形;
故选:C.
9.解:A、∵四边形ABCD是平行四边形,
又∵AB=BC,
∴四边形ABCD是菱形,故本选项不符合题意;
B、∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,故本选项不符合题意;
C、∵四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,不一定是正方形,故本选项符合题意;
D、∵四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴四边形ABCD是矩形,故本选项不符合题意;
故选:C.
10.解:A、平行四边形对角相等,正确;
B、对角线互相垂直的矩形是正方形,正确;
C、一组对边相等,且这组对边平行的四边形是平行四边形,错误;
D、菱形的对角线互相垂直平分,正确.
故选:C.
11.解:①AB=BC,∠A=90°;
根据有一个角是直角且有一组邻边相等的平行四边形是正方形,能判定 ABCD是正方形,故此选项正确;
②AC⊥BD,AC=BD;
由对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定 ABCD是正方形,故此选项正确;
③OA=OD,BC=CD;
由ABCD是平行四边形,可得AC与BD互相平分,而OA=OD,所以AC=BD,对角线相等的平行四边形是矩形,有一组邻边相等的平行四边形是菱形,既是矩形又是菱形的四边形是正方形,能判定 ABCD是正方形,故此选项正确;
④∠BOC=90°,∠ABD=∠DCA;
由∠BOC=90°,根据对角线互相垂直的平行四边形是菱形,可得 ABCD是菱形;由ABCD是平行四边形,可得AC与BD互相平分,AB∥CD,则∠ABD=∠CDB=∠DCA,所以OC=OD,又对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定 ABCD是正方形,故此选项正确.
故选:D.
12.解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;
综上所述,符合题意是D选项;
故选:D.
13.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∴∠BAE=∠BAD+DAE=150°,AB=AE,
∴∠ABE=∠AEB,
∴∠ABE=(180°﹣∠BAE)=15°,
故答案为:15°.
14.解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAD+∠DAE=90°,
∵BF⊥a于点F,DE⊥a于点E,
∴∠AFB=∠AFD=90°,
∵∠BAF+∠ABF=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中
,
∴△ABF≌△DAE,
∴AF=DE=8,BF=AE,
在Rt△ABF中,BF==6,
∴AE=6,
∴EF=AE+AF=6+8=14.
故答案为14.
15.解:∵四边形ABCD是正方形,CE=CA,
∴∠ACE=45°+90°=135°,∠E=22.5°,
∴∠AFC=90°+22.5°=112.5°.
故答案为112.5.
16.解:∵正方形的一条对角线长为8cm,
∴面积是×8×8=32cm2.
故答案为:32.
17.解:∵CE=AC,
∴∠E=∠CAE,
∵AC是正方形ABCD的对角线,
∴∠ACB=45°,
∴∠E+∠CAE=45°,
∴∠E=×45°=22.5°,
在△CEF中,∠AFC=∠E+∠ECF=22.5°+90°=112.5°.
故答案为:112.5.
18.解:如图作AF⊥x轴于F,CE⊥x轴于E.
∵四边形ABCO是正方形,
∴OA=OC,∠AOC=90°,
∵∠COE+∠AOF=90°,∠AOF+∠OAF=90°,
∴∠COE=∠OAF,
在△COE和△OAF中,
,
∴△COE≌△OAF,
∴CE=OF,OE=AF,
∵A(1,),
∴CE=OF=1,OE=AF=,
∴点C坐标(﹣,1),
故答案为(﹣,1).
19.解:∵四个全等的直角三角形的直角边分别是5和4,
∴阴影部分的正方形的边长为5﹣4=1,
∴阴影部分面积为1×1=1.
故答案为:1.
20.解:过点D作DG⊥BC于点G,
∵四边形BDCE是菱形,
∴BD=CD.
∵BC=2,∠D=60°,
∴△BCD是等边三角形,
∴BD=BC=CD=2,
∴CG=1,GD=CD sin60°=2×=,
∴D(2+,1).
故答案为:(2+,1).
21.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵等边三角形ABE,
∴AB=AE,∠BAE=∠AEB=60°,
∠DAE=∠BAD+∠BAE=90°+60°=150°,
AD=AE,
∴∠AEB=∠ABE=(180°﹣∠DAB)÷2=15°,
∴∠BED=∠AEB﹣∠AED=60°﹣15°=45°,
故答案为:45°
22.解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===2,
∴CH=,
故答案为:.
23.解:∵△ABC是等边三角形,ABDE是正方形,
∴AC=AE,
∴∠CAB=60°,∠EAB=90°,
∴∠CAE=150°,
∴∠ACE=∠AEC=15°,
∵△AEF和△ABF中,
,
∴△AEF≌△ABF(SAS),
∴∠ABF=∠AEF=15°.
故答案为:15°.
24.解:过P作EF∥AD,则PE⊥CD,PF⊥AB,
设PF=x,则AB=5+x,AF=FB=,
在直角△APF中,AP为斜边,AP=5cm,PF=x,FA=,
且AF2+PF2=AP2,
解得x=3cm,
所以AB=3cm+5cm=8cm,
故正方形面积为S=AB AB=64cm2,
故答案为 64.
25.解:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
26.解:(1)∵四边形ABCD是正方形,
∴∠BAO=∠AOC=90°,
∵E(0,2),H(﹣2,6),
∴AH=OE=2,
∵四边形EFGH是菱形,
∴EH=EF,
在Rt△AHE和Rt△OEF中,
,
∴Rt△AHE≌Rt△OEF,
∴∠AEH=∠EFO,
∵∠EFO+∠FEO=90°,
∴∠AEH+∠FEO=90°,
∴∠HEF=90°,∵四边形EFGH是菱形,
∴四边形EFGH是正方形.
(2)连接EG交FH于K.
∵HE=EF,
∴AH2+AE2=EO2+OF2,
∴AH2+16=4+25,
∴AH=,
∴H(﹣,6),
∵KH=KF,
∴K(﹣,3),
∵GK=KE,
∴G(﹣5﹣,4).
27.证明:(1)连接BD,如图:
∵四边形ABCD是平行四边形,G、H分别是AD、BC的中点,E、O、F是对角线AC的四等分点,
∴点O是对角线AC,BD的交点,
∴OB=OD,
∵G是AD的中点,
∴EG是△AOD的中位线,
∴EG∥OD,EG=OD,
同理:FH∥OB,FH=OB,
∴EG=HF,EG∥HF,
∴四边形GEHF是平行四边形;
(2)∵四边形GEHF是平行四边形,
∴GH=AB,
∵AC=2AB,
∴AB=AC=EF,
∴GH=EF,
∴四边形GEHF是矩形;
故答案为:矩;
(3))∵四边形GEHF是平行四边形,
∴GH=AB,
∵AC=2AB,
∴AB=AC=EF,
∴GH=EF,
∴四边形GEHF是矩形,
∵AC⊥AB,
∴EG⊥EH,
∴矩形GEFH是正方形.
故答案为:AC=2AB,AC⊥AB.
28.证明:(1)∵平行四边形BCED,
∴CE∥BD,CE=BD,
∵D为AB中点,
∴AD=BD,
∴CE∥AD,CE=AD,
∴四边形ADCE为平行四边形,
又BC∥DE,
∴∠AFD=∠ACB=90°,
∴AC⊥DE,
故四边形ADCE为菱形;
(2)在Rt△ABC中,∵AB=8,AC=6,
∴BC=,
∵D为AB中点,F也为AC的中点,
∴DF=,
∴四边形ADCE的面积=AC×DF=6;
(3)应添加条件AC=BC.
证明:∵AC=BC,D为AB中点,
∴CD⊥AB(三线合一的性质),即∠ADC=90°.
∵四边形BCED为平行四边形,四边形ADCE为平行四边形,
∴DE=BC=AC,∠AFD=∠ACB=90°.
∴四边形ADCE为正方形.(对角线互相垂直且相等的四边形是正方形)
1.正方形具有而矩形不具有的性质是( )
A.对角相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
2.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣3,0),B(2,b),则正方形ABCD的面积是( )
A.20 B.16 C.34 D.25
3.对角线互相垂直平分但不相等的四边形是( )
A.菱形 B.矩形 C.正方形 D.平行四边形
4.正方形具有而菱形不具备的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线平分一组对角 D.对角线相等
5.如图,将边长为2cm的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
A.() B.(2,﹣1) C.(1,) D.(﹣1,)
6.如图,两张对边平行且等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
7.两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
8.下列说法中,正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.矩形的对角线互相垂直
C.菱形的对角线互相垂直且平分
D.对角线互相垂直,且相等的四边形是正方形
9.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,平行四边形ABCD是菱形
B.当AC⊥BD时,平行四边形ABCD是菱形
C.当AC=BD时,平行四边形ABCD是正方形
D.当∠ABC=90°时,平行四边形ABCD是矩形
10.下列说法不正确的是( )
A.平行四边形对角相等
B.对角线互相垂直的矩形是正方形
C.一组对边相等另一组对边平行的四边形是平行四边形
D.菱形的对角线互相垂直平分
11.如图,下列四组条件中,能判定 ABCD是正方形的有( )
①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.
A.1个 B.2个 C.3个 D.4个
12.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
二.填空题(共12小题)
13.如图,以正方形ABCD的一边AD为边向外作等边△ADE,则∠ABE的度数是 .
14.如图,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,AB=10,则EF的长为 .
15.正方形ABCD的边BC的延长线上取一点E,使CE=AC,AE与CD交于点F,则∠AFC= 度.
16.已知正方形的一条对角线长为8cm,则其面积是 cm2.
17.如图,点E是正方形ABCD的边BC延长线上的一点,且CE=AC,若AE交CD于点F,则∠AFC= °.
18.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为 .
19.如图,由四个直角边分别为5和4的全等直角三角形拼成“赵爽弦图”,其中阴影部分面积为 .
20.如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是 .
21.如图,等边△ABE与正方形ABCD有一条公共边,点E在正方形外,连接DE,则∠BED= °.
22.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
23.如图,在等边△ABC的外侧作正方形ABDE,AD与CE交于F,则∠ABF的度数为 .
24.如图,已知点P为正方形ABCD内一点,且PA=PB=5cm,点P到边CD的距离也为5cm,则正方形ABCD的面积为 cm2.
三.解答题(共2小题)
25.如图,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,ED=EC.求证:四边形DFCE是正方形.
26.如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
(1)当H(﹣2,6)时,求证:四边形EFGH是正方形;
(2)若F(﹣5,0),求点G的坐标.
27.如图,在 ABCD中,G、H分别是AD、BC的中点,E、O、F是对角线AC的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)若AC=2AB,则四边形GEHF是 形;
(3)当AC、AB满足 时,四边形GEHF是正方形.
28.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,四边形BCED为平行四边形,DE、AC相交于F,连接DC、AE.
(1)试确定四边形ADCE的形状,并说明理由;
(2)若AB=8,AC=6,求四边形ADCE的面积;
(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.
参考答案
1.解:因为正方形的对角相等,对角线相等、垂直、且互相平分,矩形的对角相等,对角线相等,互相平分,
所以正方形具有而矩形不具有的性质是对角线互相垂直.
故选:D.
2.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣3,0),B(2,b),
∴OA=3,OM=2,
∴OD=AM=5,
∴AD==,
∴正方形ABCD的面积=34,
故选:C.
3.解:A、菱形的对角线互相垂直平分,且不相等,故本选项正确;
B、矩形的对角线互相平分,且相等,故本选项错误;
C、正方形的对角线互相垂直平分,且相等,故本选项错误;
D、平行四边形的对角线互相平分,故本选项错误.
故选:A.
4.解:A、对角线互相平分,正方形和菱形都具有,故本选项不符合题意;
B、对角线互相垂直,正方形和菱形都具有,故本选项不符合题意;
C、对角线平分一组对角,正方形和菱形都具有,故本选项不符合题意;
D、正方形对角线相等,菱形对角线不相等,故本选项符合题意.
故选:D.
5.解:作AD⊥y轴于D,作CE⊥y轴于E,如图所示:
则∠ADO=∠OEC=90°,
∴∠1+∠2=90°,
∵点A的坐标为(1,),
∴AD=1,OD=,
∵四边形OABC是正方形,
∴∠AOC=90°,OC=AO,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCE和△AOD中,
,
∴△OCE≌△AOD(AAS),
∴OE=AD=1,CE=OD=,
∴点C的坐标为(,﹣1).
故选:A.
6.
解:由图可知,过A点作AE⊥BC于E,AF⊥CD于F,
∵两条纸条宽度相等,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵SABCD=BC×AE=CD AF.
又∵AE=AF,
∴BC=CD,
∴四边形ABCD为菱形.
故选:B.
7.解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
8.解:A错误,如等腰梯形即为一组对边平行,另一组对边相等的四边形,却不是平行四边形;
B错误,由矩形的性质可知矩形的对角线互相平分且相等;
C正确,由菱形的性质可知菱形的对角线互相垂直且平分;
D错误,由正方形的性质及判定可知,对角线互相垂直,平分,且相等的四边形是正方形;
故选:C.
9.解:A、∵四边形ABCD是平行四边形,
又∵AB=BC,
∴四边形ABCD是菱形,故本选项不符合题意;
B、∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,故本选项不符合题意;
C、∵四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,不一定是正方形,故本选项符合题意;
D、∵四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴四边形ABCD是矩形,故本选项不符合题意;
故选:C.
10.解:A、平行四边形对角相等,正确;
B、对角线互相垂直的矩形是正方形,正确;
C、一组对边相等,且这组对边平行的四边形是平行四边形,错误;
D、菱形的对角线互相垂直平分,正确.
故选:C.
11.解:①AB=BC,∠A=90°;
根据有一个角是直角且有一组邻边相等的平行四边形是正方形,能判定 ABCD是正方形,故此选项正确;
②AC⊥BD,AC=BD;
由对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定 ABCD是正方形,故此选项正确;
③OA=OD,BC=CD;
由ABCD是平行四边形,可得AC与BD互相平分,而OA=OD,所以AC=BD,对角线相等的平行四边形是矩形,有一组邻边相等的平行四边形是菱形,既是矩形又是菱形的四边形是正方形,能判定 ABCD是正方形,故此选项正确;
④∠BOC=90°,∠ABD=∠DCA;
由∠BOC=90°,根据对角线互相垂直的平行四边形是菱形,可得 ABCD是菱形;由ABCD是平行四边形,可得AC与BD互相平分,AB∥CD,则∠ABD=∠CDB=∠DCA,所以OC=OD,又对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定 ABCD是正方形,故此选项正确.
故选:D.
12.解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;
综上所述,符合题意是D选项;
故选:D.
13.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∴∠BAE=∠BAD+DAE=150°,AB=AE,
∴∠ABE=∠AEB,
∴∠ABE=(180°﹣∠BAE)=15°,
故答案为:15°.
14.解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAD+∠DAE=90°,
∵BF⊥a于点F,DE⊥a于点E,
∴∠AFB=∠AFD=90°,
∵∠BAF+∠ABF=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中
,
∴△ABF≌△DAE,
∴AF=DE=8,BF=AE,
在Rt△ABF中,BF==6,
∴AE=6,
∴EF=AE+AF=6+8=14.
故答案为14.
15.解:∵四边形ABCD是正方形,CE=CA,
∴∠ACE=45°+90°=135°,∠E=22.5°,
∴∠AFC=90°+22.5°=112.5°.
故答案为112.5.
16.解:∵正方形的一条对角线长为8cm,
∴面积是×8×8=32cm2.
故答案为:32.
17.解:∵CE=AC,
∴∠E=∠CAE,
∵AC是正方形ABCD的对角线,
∴∠ACB=45°,
∴∠E+∠CAE=45°,
∴∠E=×45°=22.5°,
在△CEF中,∠AFC=∠E+∠ECF=22.5°+90°=112.5°.
故答案为:112.5.
18.解:如图作AF⊥x轴于F,CE⊥x轴于E.
∵四边形ABCO是正方形,
∴OA=OC,∠AOC=90°,
∵∠COE+∠AOF=90°,∠AOF+∠OAF=90°,
∴∠COE=∠OAF,
在△COE和△OAF中,
,
∴△COE≌△OAF,
∴CE=OF,OE=AF,
∵A(1,),
∴CE=OF=1,OE=AF=,
∴点C坐标(﹣,1),
故答案为(﹣,1).
19.解:∵四个全等的直角三角形的直角边分别是5和4,
∴阴影部分的正方形的边长为5﹣4=1,
∴阴影部分面积为1×1=1.
故答案为:1.
20.解:过点D作DG⊥BC于点G,
∵四边形BDCE是菱形,
∴BD=CD.
∵BC=2,∠D=60°,
∴△BCD是等边三角形,
∴BD=BC=CD=2,
∴CG=1,GD=CD sin60°=2×=,
∴D(2+,1).
故答案为:(2+,1).
21.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵等边三角形ABE,
∴AB=AE,∠BAE=∠AEB=60°,
∠DAE=∠BAD+∠BAE=90°+60°=150°,
AD=AE,
∴∠AEB=∠ABE=(180°﹣∠DAB)÷2=15°,
∴∠BED=∠AEB﹣∠AED=60°﹣15°=45°,
故答案为:45°
22.解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===2,
∴CH=,
故答案为:.
23.解:∵△ABC是等边三角形,ABDE是正方形,
∴AC=AE,
∴∠CAB=60°,∠EAB=90°,
∴∠CAE=150°,
∴∠ACE=∠AEC=15°,
∵△AEF和△ABF中,
,
∴△AEF≌△ABF(SAS),
∴∠ABF=∠AEF=15°.
故答案为:15°.
24.解:过P作EF∥AD,则PE⊥CD,PF⊥AB,
设PF=x,则AB=5+x,AF=FB=,
在直角△APF中,AP为斜边,AP=5cm,PF=x,FA=,
且AF2+PF2=AP2,
解得x=3cm,
所以AB=3cm+5cm=8cm,
故正方形面积为S=AB AB=64cm2,
故答案为 64.
25.解:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
26.解:(1)∵四边形ABCD是正方形,
∴∠BAO=∠AOC=90°,
∵E(0,2),H(﹣2,6),
∴AH=OE=2,
∵四边形EFGH是菱形,
∴EH=EF,
在Rt△AHE和Rt△OEF中,
,
∴Rt△AHE≌Rt△OEF,
∴∠AEH=∠EFO,
∵∠EFO+∠FEO=90°,
∴∠AEH+∠FEO=90°,
∴∠HEF=90°,∵四边形EFGH是菱形,
∴四边形EFGH是正方形.
(2)连接EG交FH于K.
∵HE=EF,
∴AH2+AE2=EO2+OF2,
∴AH2+16=4+25,
∴AH=,
∴H(﹣,6),
∵KH=KF,
∴K(﹣,3),
∵GK=KE,
∴G(﹣5﹣,4).
27.证明:(1)连接BD,如图:
∵四边形ABCD是平行四边形,G、H分别是AD、BC的中点,E、O、F是对角线AC的四等分点,
∴点O是对角线AC,BD的交点,
∴OB=OD,
∵G是AD的中点,
∴EG是△AOD的中位线,
∴EG∥OD,EG=OD,
同理:FH∥OB,FH=OB,
∴EG=HF,EG∥HF,
∴四边形GEHF是平行四边形;
(2)∵四边形GEHF是平行四边形,
∴GH=AB,
∵AC=2AB,
∴AB=AC=EF,
∴GH=EF,
∴四边形GEHF是矩形;
故答案为:矩;
(3))∵四边形GEHF是平行四边形,
∴GH=AB,
∵AC=2AB,
∴AB=AC=EF,
∴GH=EF,
∴四边形GEHF是矩形,
∵AC⊥AB,
∴EG⊥EH,
∴矩形GEFH是正方形.
故答案为:AC=2AB,AC⊥AB.
28.证明:(1)∵平行四边形BCED,
∴CE∥BD,CE=BD,
∵D为AB中点,
∴AD=BD,
∴CE∥AD,CE=AD,
∴四边形ADCE为平行四边形,
又BC∥DE,
∴∠AFD=∠ACB=90°,
∴AC⊥DE,
故四边形ADCE为菱形;
(2)在Rt△ABC中,∵AB=8,AC=6,
∴BC=,
∵D为AB中点,F也为AC的中点,
∴DF=,
∴四边形ADCE的面积=AC×DF=6;
(3)应添加条件AC=BC.
证明:∵AC=BC,D为AB中点,
∴CD⊥AB(三线合一的性质),即∠ADC=90°.
∵四边形BCED为平行四边形,四边形ADCE为平行四边形,
∴DE=BC=AC,∠AFD=∠ACB=90°.
∴四边形ADCE为正方形.(对角线互相垂直且相等的四边形是正方形)
