六年级数学下册课件-6.2.2 图形的运动-人教版(共17张PPT)
文档属性
| 名称 | 六年级数学下册课件-6.2.2 图形的运动-人教版(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-23 20:02:22 | ||
图片预览




文档简介
(共17张PPT)
图形的运动
情境导入
(1)你知道图形运动的方式有哪些?
(2)在这些运动中哪些运动不改变图形的形状和大小?
(3)哪些运动只改变图形的大小,而不改变形状?
图形的运动
探索新知
小学阶段学过平移、旋转、轴对称、图形的放大和缩小。
探索新知
小学阶段学过平移、旋转、轴对称、图形的放大和缩小。
平移与旋转 放大与缩小
不同点 不改变图形的形状和大小,只改变图形的位置。 不改变图形的形状,只改变图形的大小。
相同点 都不改变图形的形状。
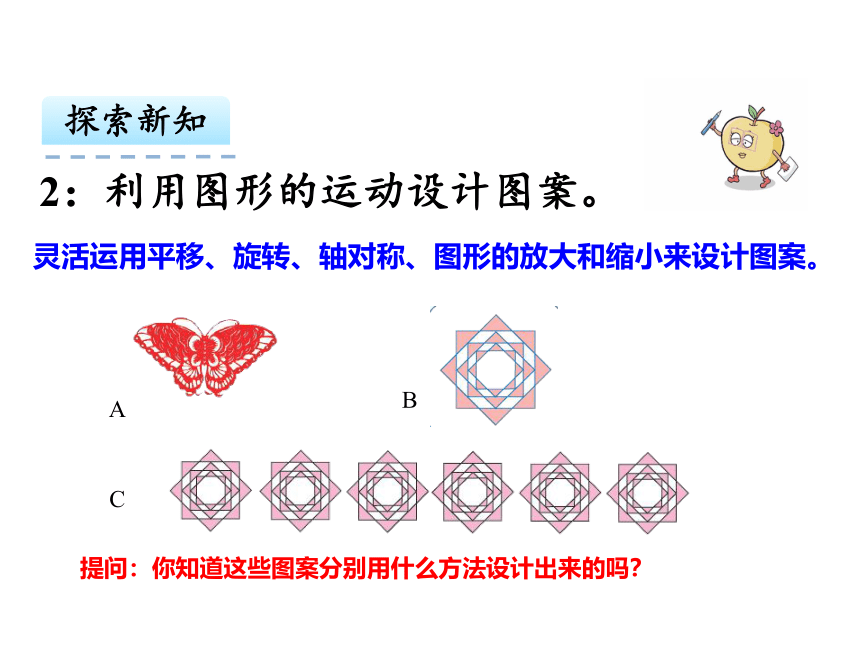
2:利用图形的运动设计图案。
灵活运用平移、旋转、轴对称、图形的放大和缩小来设计图案。
提问:你知道这些图案分别用什么方法设计出来的吗?
A
B
C
探索新知
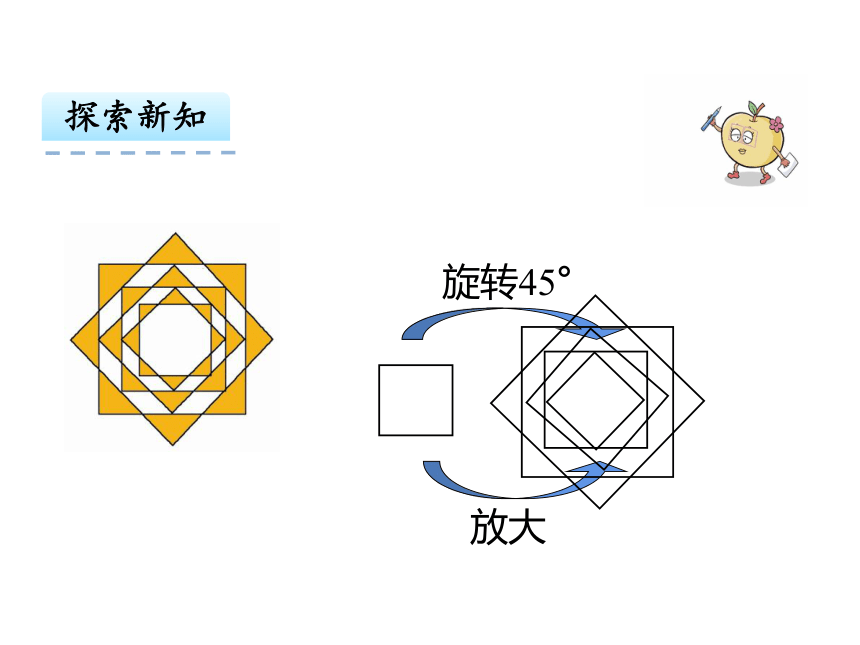
旋转45°
放大
探索新知
探索新知
在同一平面内,将一个图形上的所有点都按照某个方向作相同距离的移动,这样的运动叫做图形的平移。
平移不改变图形的大小和形状,只是图形的位置发生变化。
在方格纸上平移图形要把握两点:一是移动的方向,二是移动的距离。
平移
探索新知
旋转
在平面内,将一个图形绕一个点,并按某个方向转动一定的角度,这样的运动叫图形的旋转。
在方格纸上画旋转图形时要把握住两点: 一是中心点;二是旋转的方向和角度。
图形的旋转不改变图形的形状和大小。只是图形的位置发生改变。
探索新知
轴对称
一个图形,如果沿一条直线对折,直线两边的部分能够完全重合,这样的图形叫做轴对称图形。折痕所在的这条直线叫做对称轴。
画轴对称图形的另一半时,抓住“在轴对称图形中,对称轴两侧相对的点到对称轴的距离相等”来画。
探索新知
对称图形(会画对称轴):
像这样,把一个图形对折后,两部分能完全重合,我们就把这样的图形叫做轴对称图形。
探索新知
图形 对称轴数量 图形 对称轴数量
线段 菱形
角 等腰梯形
等腰三角形 圆
等边三角形 环形
长方形 扇形
正方形 半圆
常见轴对称图形的对称轴数量
1条
1条
3条
2条
4条
2条
1条
1条
无数条
无数条
1条
1条
探索新知
按一定的比,将一个图形放大或缩小,叫做图形的缩放。
图形的放大与缩小,改变了图形的大小,图形的形状没变。
图形的放大和缩小
探索新知
相同点
不同点
1.边的长度按一定的倍数放大或缩小,图形的大小发生变化。图形的形状不变。
2.比的前项表示变化后的长度,比的后项表示原来的长度。
比值大于1(如2∶1),表示图形放大到原来的2倍。
比值小于1(如1∶3),表示图形缩小到原来的 。
图形的放大与缩小的区别与联系
探索新知
学以致用
1.
图中A→B→C →D 是怎样变过来的?
(1)A经过向右平移5个格得到的到B。
(2)B先向右平移5个格,再绕中心点逆时针旋转90°得到C 。
或者先逆时针旋转90°,再向右平移5个格得到到C。
(3)C先向右平移5个格,再绕中心点逆时针旋转90°得到D。
或者先绕中心点旋转90°,再向右平移5个格得到D。
A B C D
学以致用
2.下面4个图形的涂色部分面积相等吗?为什么?
从表面上看涂色部分的面积不相等,但是通过平移、旋转、拼接等方法都可以转化得到最后一幅图。
课堂小结
图形
变换
全等变换
相似变换
平移
旋转
轴对称
图形的放大
图形的缩小
(形状不变,
大小改变)
(形状不变,
大小不变)
向右平移
向下平移
向左平移
向上平移
顺时针方向旋转
逆时针方向旋转
图形的运动
情境导入
(1)你知道图形运动的方式有哪些?
(2)在这些运动中哪些运动不改变图形的形状和大小?
(3)哪些运动只改变图形的大小,而不改变形状?
图形的运动
探索新知
小学阶段学过平移、旋转、轴对称、图形的放大和缩小。
探索新知
小学阶段学过平移、旋转、轴对称、图形的放大和缩小。
平移与旋转 放大与缩小
不同点 不改变图形的形状和大小,只改变图形的位置。 不改变图形的形状,只改变图形的大小。
相同点 都不改变图形的形状。
2:利用图形的运动设计图案。
灵活运用平移、旋转、轴对称、图形的放大和缩小来设计图案。
提问:你知道这些图案分别用什么方法设计出来的吗?
A
B
C
探索新知
旋转45°
放大
探索新知
探索新知
在同一平面内,将一个图形上的所有点都按照某个方向作相同距离的移动,这样的运动叫做图形的平移。
平移不改变图形的大小和形状,只是图形的位置发生变化。
在方格纸上平移图形要把握两点:一是移动的方向,二是移动的距离。
平移
探索新知
旋转
在平面内,将一个图形绕一个点,并按某个方向转动一定的角度,这样的运动叫图形的旋转。
在方格纸上画旋转图形时要把握住两点: 一是中心点;二是旋转的方向和角度。
图形的旋转不改变图形的形状和大小。只是图形的位置发生改变。
探索新知
轴对称
一个图形,如果沿一条直线对折,直线两边的部分能够完全重合,这样的图形叫做轴对称图形。折痕所在的这条直线叫做对称轴。
画轴对称图形的另一半时,抓住“在轴对称图形中,对称轴两侧相对的点到对称轴的距离相等”来画。
探索新知
对称图形(会画对称轴):
像这样,把一个图形对折后,两部分能完全重合,我们就把这样的图形叫做轴对称图形。
探索新知
图形 对称轴数量 图形 对称轴数量
线段 菱形
角 等腰梯形
等腰三角形 圆
等边三角形 环形
长方形 扇形
正方形 半圆
常见轴对称图形的对称轴数量
1条
1条
3条
2条
4条
2条
1条
1条
无数条
无数条
1条
1条
探索新知
按一定的比,将一个图形放大或缩小,叫做图形的缩放。
图形的放大与缩小,改变了图形的大小,图形的形状没变。
图形的放大和缩小
探索新知
相同点
不同点
1.边的长度按一定的倍数放大或缩小,图形的大小发生变化。图形的形状不变。
2.比的前项表示变化后的长度,比的后项表示原来的长度。
比值大于1(如2∶1),表示图形放大到原来的2倍。
比值小于1(如1∶3),表示图形缩小到原来的 。
图形的放大与缩小的区别与联系
探索新知
学以致用
1.
图中A→B→C →D 是怎样变过来的?
(1)A经过向右平移5个格得到的到B。
(2)B先向右平移5个格,再绕中心点逆时针旋转90°得到C 。
或者先逆时针旋转90°,再向右平移5个格得到到C。
(3)C先向右平移5个格,再绕中心点逆时针旋转90°得到D。
或者先绕中心点旋转90°,再向右平移5个格得到D。
A B C D
学以致用
2.下面4个图形的涂色部分面积相等吗?为什么?
从表面上看涂色部分的面积不相等,但是通过平移、旋转、拼接等方法都可以转化得到最后一幅图。
课堂小结
图形
变换
全等变换
相似变换
平移
旋转
轴对称
图形的放大
图形的缩小
(形状不变,
大小改变)
(形状不变,
大小不变)
向右平移
向下平移
向左平移
向上平移
顺时针方向旋转
逆时针方向旋转
