第二章 第3节气体的等压变化和等容变化基础训练(Word版含答案)
文档属性
| 名称 | 第二章 第3节气体的等压变化和等容变化基础训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 932.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-24 19:12:59 | ||
图片预览




文档简介
2019人教版选择性必修第三册 第二章 第3节 气体的等压变化和等容变化 基础训练
一、多选题
1.一定量的理想气体从状态a开始,经历等温或等压过程ab、bc、cd、da回到原状态,其p-T图象如图所示,其中对角线ac的延长线过原点O。下列判断正确的是( )
A.在过程da中气体的内能增加,体积减小
B.在整个过程气体对外界做的功大于外界对气体做的功
C.在过程cd中气体向外界放出的热量等于外界对气体做的功
D.气体在状态a的单位体积分子数大于在状态c的单位体积分子数
E.若将过程ab改为绝热过程且压强变化相同,则状态的温度小于状态b的温度
2.下列说法正确的是( )
A.扩散现象在气体、液体和固体中都能发生
B.热量不可能从低温物体传到高温物体
C.一定质量的某种理想气体在等压膨胀的过程中,内能一定增加
D.布朗运动是液体分子对液体中悬浮微粒的撞击作用不平衡的结果
E.某气体的摩尔体积为V,每个分子的体积为,则阿伏加德罗常数可表示为
3.某同学用带有刻度的注射器做验证玻意耳定律的实验,温度计表明在图中的图线可以得出( )
A.如果实验是从E状态→F状态,则表示外界有空气进入注射器内
B.如果实验是从E状态→F状态,则表示注射器内有部分空气漏了出来
C.如果实验是从F状态→E状态,则表示注射器内有部分空气漏了出来
D.如果实验是从F状态→E状态,则表示外界有空气进入注射器内
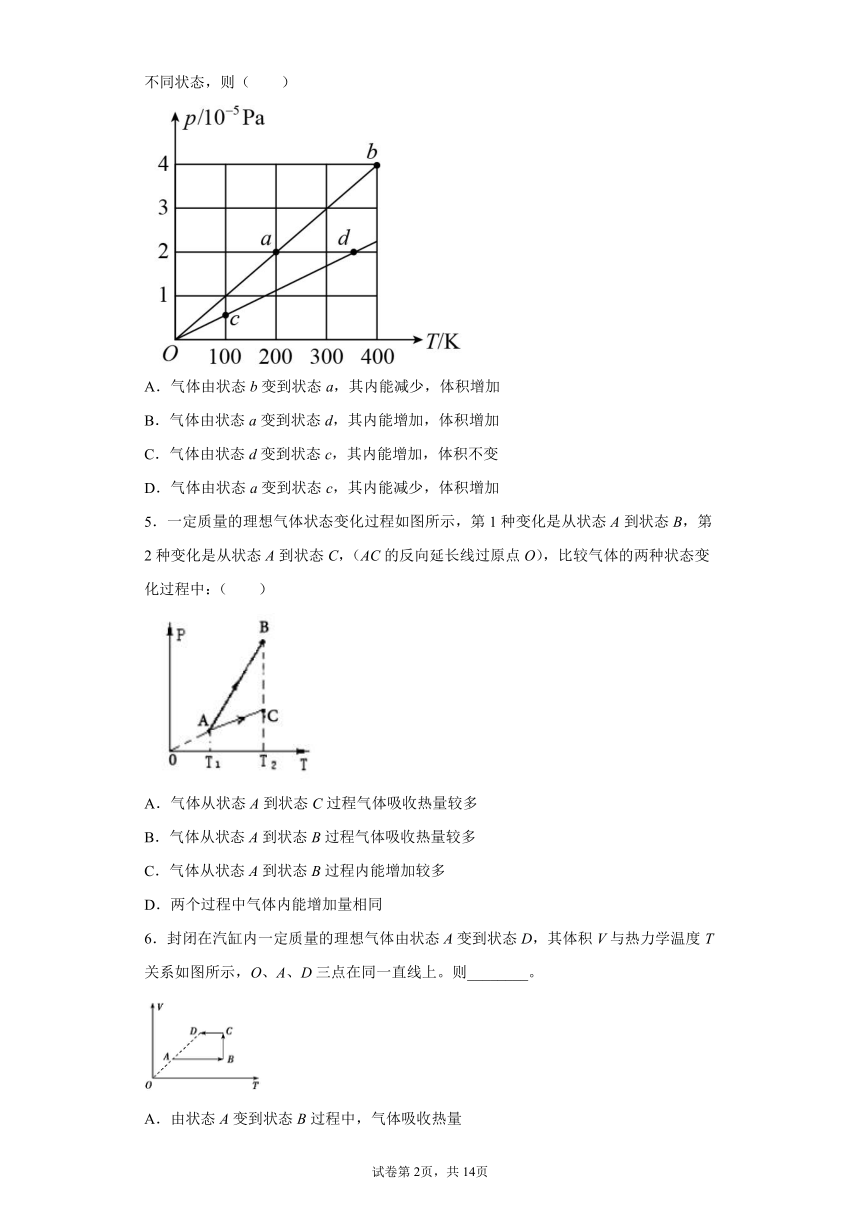
4.如图所示为一定质量的理想气体在不同体积时的两条等容线,a、b、c、d表示四个不同状态,则( )
A.气体由状态b变到状态a,其内能减少,体积增加
B.气体由状态a变到状态d,其内能增加,体积增加
C.气体由状态d变到状态c,其内能增加,体积不变
D.气体由状态a变到状态c,其内能减少,体积增加
5.一定质量的理想气体状态变化过程如图所示,第1种变化是从状态A到状态B,第2种变化是从状态A到状态C,(AC的反向延长线过原点O),比较气体的两种状态变化过程中:( )
A.气体从状态A到状态C过程气体吸收热量较多
B.气体从状态A到状态B过程气体吸收热量较多
C.气体从状态A到状态B过程内能增加较多
D.两个过程中气体内能增加量相同
6.封闭在汽缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度T关系如图所示,O、A、D三点在同一直线上。则________。
A.由状态A变到状态B过程中,气体吸收热量
B.由状态B变到状态C过程中,气体从外界吸收热量,内能增加
C.C状态气体的压强小于D状态气体的压强
D.D状态时单位时间内与器壁单位面积碰撞的分子数比A状态少
E.C状态到D状态,单位时间内与器壁单位面积碰撞的分子数减少
7.如图所示,为一定质量的理想气体发生状态变化的p-V图象,图线1、2是两条等温线,A、B是等温线1上的两点,C、D是等温线2上的两点,图线AD、BC均与V轴平行,则下列说法正确的是( )
A.等温线2对应的气体温度比等温线1对应的气体温度高
B.气体从状态A变化到状态B,气体吸收的热量比气体对外界做功多
C.气体从状态B变化到状态C,气体吸收的热量比气体对外界做功多
D.气体从状态C变化到状态D,单位体积的气体分子数增大,但气体分子的平均动能不变
E.气体从状态D变化到状态A,气体放出的热量比外界对气体做功少,气体内能增加
8.如图所示为一定质量的理想气体沿箭头所示的方向发生状态变化的过程,则关于该气体压强变化的下列说法中正确的是( )
A.从状态c到状态d的过程中,压强一直减小
B.从状态d到状态a的过程中,压强一直增大
C.从状态a到状态b的过程中,压强先增大后减小
D.从状态b到状态c的过程中,压强先增大后减小
9.一定质量的理想气体状态变化如图所示,则( )
A.状态b、c的内能相等
B.状态a的内能比状态b、c的内能大
C.由a到b的过程中气体向外界放热
D.由b到c的过程中气体一直向外界放热
二、单选题
10.如图,绝热的容器内封闭一定质量的理想气体(不考虑分子势能,外界大气压恒定),用电阻丝对其加热时,绝热活塞缓慢地无摩擦地上升,下列正确的是( )
A.活塞上升,气体体积增大,温度降低
B.气体从电阻丝吸收热量,气体又对外做功,气体内能可能不变
C.气体从电阻丝吸收的热量一定大于气体对外做功
D.气体体积增大,单位时间内打到器壁单位面积的分子数减少,气体压强一定减小
11.回热式制冷机是一种深低温设备,制冷极限约50K,某台设备工作时,一定量的氦气(可视为理想气体)缓慢经历如图所示的四个过程:从状态A到B和C到D是等温过程,温度分别为t1=27℃和t2=-133℃;从状态B到C和D到A是等容过程,体积分别为V0和5V0,则状态B与D的压强之比是( )
A.7∶3 B.15∶7 C.133∶27 D.75∶7
12.如图所示,一导热性能良好的气缸吊在弹簧下,缸内被活塞封住一定质量的气体(不计活塞与缸壁摩擦),当温度升高到某一数值时,变化了的量有:( )
A.活塞高度h B.气体压强p C.缸体高度H D.弹簧长度L
13.一定质量的某种理想气体的压强为,热力学温度为,单位体积内的气体分子数为,则( )
A.增大,一定增大
B.减小,一定增大
C.增大时,一定增大
D.增大时,一定减小
14.一定质量的理想气体按的顺序经历一系列状态变化,其图像如图所示。图中线段与纵轴平行,线段与纵轴垂直。气体在状态变化过程中下列叙述正确的是( )
A.过程气体体积增加
B.过程气体不放热也不吸热
C.过程气体分子在单位时间内撞击单位面积容器壁的次数增加
D.过程气体对外界做的功小于过程外界对气体做的功
15.一个密闭的钢管内装有空气,在温度为20℃时,压强为1atm,若温度上升到80℃,管内空气的压强约为( )
A.4atm B. C.1.2atm D.
16.图示为竖直放置、上细下粗、两端封闭的玻璃细管,水银柱将气体分隔成A、B两部分,初始温度相同.缓缓加热气体,使A、B升高相同温度,系统稳定后,A、B两部分气体对液面压力的变化量分别为△FA和△FB,压强变化量分别为△pA和△pB.则( )
A.水银柱向下移动了一段距离
B.水银柱不发生移动
C.△FA<△FB
D.△pA=△pB
17.两端封闭且内径均匀的直玻璃管,水平放置,如图所示,左、右两端空气柱的体积关系为,温度均为20℃,现将右端空气柱降为0℃,左端空气柱降为10℃,则管中水银柱将( )
A.不动 B.向左移动
C.向右移动 D.无法确定是否移动
三、解答题
18.胎压监测装置是在汽车行驶过程中对轮胎气压进行实时自动监测的装置。一辆长期停放的汽车,某车胎内气体温度为27℃,胎压监测装置显示该车胎实际气压为200kPa,考虑到胎压不足,司机驾驶车辆到汽车修理店充气,行驶一段路程到汽车修理店后,胎压监刻装置显示该车胎胎压为210kPa,工作人员为该车胎充气,充气完毕后汽车停放一段时间,胎内气体温度恢复到27℃时,胎压监刻装置显示该车胎胎压为250kPa,若不考虑轮胎内气体体积变化。求:
(1)车胎胎压为210kPa时轮胎内气体温度为多少摄氏度;
(2)新充入气体与车胎内原来气体的质量比。
19.某氮气气弹簧撑开时,腔体内气体的体积约为,压强为,温度为27℃。在压强为、0℃时氮气的密度为。已知氮气的摩尔质量为,阿伏伽德罗常数为,请估算腔体内气体的分子数(计算结果保留一位有效数字)
20.如图所示,一定质量理想气体经历A→B的等压过程,B→C的绝热过程(气体与外界无热量交换),其中B→C过程中内能减少900J。求A→B→C过程中气体对外界做的总功。
(1)过程气体对外做的功;
(2)过程气体对外做的功;
(3)A→B→C过程中气体对外界做的总功。
21.如图所示,水平面上固定着开口向上的汽缸,质量m=5 kg、横截面积S =50 cm2 的活塞密封了一定质量的理想气体,一根轻绳一端系在活塞上,另一端跨过两个定滑轮连着一根劲度系数k=500 N/m的竖直轻弹簧,弹簧的下端系一质量M=5 kg的物块。开始时,缸内气体的温度t1 =27℃,活塞到缸底的距离L1 =120cm,弹簧恰好处于原长。已知大气压强p0 =1.0 ×105Pa,不计一切摩擦,现使缸内气体缓慢冷却,求
(i)物块恰好离开桌面时,缸内气体的温度t2;
(ii)缸内气体的温度降低到-48℃时,物块离桌面的高度h。
22.如图所示,在长为l=57cm的一端封闭、另端开口向上的竖直玻璃管内,用4cm高的水银柱封闭着51cm长的理想气体,管内外气体的温度均为33℃.
(1)现将水银徐徐注入管中,直到水银面与管口相平,此时管中气体的压强为多少
(2)接着(1)中问题缓慢对玻璃管加热升温至多少时,管中刚好只剩下4cm高的水银柱 (大气压强为p0=76cmHg)
23.如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体.活塞的质量为m,横截面积为S,与容器底部相距h.现通过电热丝缓慢加热气体,当气体的温度为T1时活塞上升了h.已知大气压强为p0.重力加速度为g,不计活塞与气缸间摩擦.
①求温度为T1时气体的压强;
②现停止对气体加热,同时在活塞上缓慢添加砂粒,当添加砂粒的质量为m0时,活塞恰好回到原来位置,求此时气体的温度.
24.某同学设计的简易火灾报警装置如图所示,竖直固定、上端开口的试管中装有高h=20cm的水银.其下方封闭有一段气柱。当环境温度为57℃时,电路恰好接通,电铃D发出报警声。取绝对零度为-273℃。
①若环境温度缓慢降至27℃时,水银柱下降了△L=5cm,试求环境温度为57℃时,试管内封闭气柱的长度L;
②若使环境温度降低,并且往玻璃管内注入高△h=4 cm的水银时,报警装置恰好再次报警,求此时的环境温度t(已知大气压强p0= 76 cmHg)。
25.一定质量理想气体的体积V与热力学温度T的关系如图所示,气体在状态A的压强为pA=1.5p0,温度TA=1.5T0,线段AB与V轴平行,BC的延长线过原点。求:
(1)B点的压强pB:
(2)气体从状态A变化到状态B的过程中,对外界做的功为50J,则该过程中吸收的热量Q;
(3)状态C的温度Tc。
26.如图所示,倾角为的光滑斜面上有一固定挡板O,现有一质量为M的气缸,气缸内用质量为m的活塞封闭有一定质量的理想气体,活塞与气缸间光滑,活塞横截面为S,现将活塞用细绳固定在挡板O上处于静止状态。(已知外界大气压强为P0)求:
(1)气缸内的气体压强P1;
(2)若将绳子剪断,气缸与活塞保持相对静止一起沿斜面向下做匀加速直线运动,试计算气缸内的气体压强P2。
27.如图所示,粗细均匀的、一端封闭一端开口的U形玻璃管,当t1=31 ℃、大气压强p0=1atm时,两管水银面相平,这时左管被封闭气柱长l1=8 cm。求:
(1)当温度t2等于多少时,左管气柱长l2为9 cm
(2)当温度达到上问中温度t2时,为使左管气柱长l3为8 cm,则应在右管再加多高的水银柱?
28.如图(甲)所示为一下粗上细且上端开口的薄壁玻璃管,管内有一部分水银封住密闭气体,上管足够长,图中大小截面积分别为S1=2cm2、S2=1cm2,粗细管内水银长度分别为h1=h2=2cm,封闭气体长度为L=22cm。大气压强为p0=76cmHg,气体初始温度为57。求:
(1)若缓慢升高气体温度,升高至多少开尔文方可将所有水银全部挤入细管内;
(2)若温度升高至492K,液柱下端离开玻璃管底部的距离;
(3)在图(乙)中作出全过程的p-V图象。
29.如图,圆柱形导热气缸长,缸内用活塞(质量和厚度均不计)密闭了一定质量的理想气体,缸底装有一个触发器D,当缸内压强达到时,D被触发,不计活塞与缸壁的摩擦。初始时,活塞位于缸口处,环境温度,压强。
(1)若环境温度不变,缓慢向下推活塞,求D刚好被触发时,到缸底的距离;
(2)若活塞固定在缸口位置,缓慢升高环境温度,求D刚好被触发时的环境温度。
30.如图所示,一根粗细均匀、内壁光滑、竖直放置的薄壁玻璃管下端密封,上端封闭但留有一气孔与外界大气相连。管内下端有被活塞封住的一定量的理想气体,设外界大气压强为p0,活塞因重力而产生的压强为0.5p0,开始时,气体温度为T1,活塞上方的气体的体积为0.5V1,活塞下方玻璃管的容积为V1。现对活塞下端密封的气体缓慢加热。求:
(1)活塞刚碰到玻璃管顶部时,气体的温度;
(2)当气体温度达到1.8T1时,气体的压强。
31.冬季南北方气温差异很大,若在某一时刻海南三亚地区的气温为27℃,而此时黑龙江北部的漠河地区气温为-33℃.在这一时刻有一个容积为2.5 L的足球放在了三亚,足球内部的空气压强为2.0×105Pa,假设足球的容积不变,热力学温度与摄氏温度的关系为T=t+273 K,室外空气压强声p0=1.0×105 Pa.
(i)若足球此时放在漠河,求足球内部的空气压强;
(ii)若足球此时放在漠河,并用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压强相同的气体打进球内,求打多少次才能让足球内部空气压强恢复到2.0×10 5 Pa (打气过程中假设足球内的气体温度不变)
32.在室温为17℃时给一个篮球充气使其压强达到,室内外大气压强均为,设在下述整个过程中篮球体积不变。
(1)在球场比赛时温度升高到37℃,这时球内压强有多大?(结果保留两位有效数字)
(2)由于漏气,当篮球内气体的压强变为,温度仍为17℃时,求球内剩下的空气与漏出空气的质量比值。
33.如图所示,竖直放置的粗细均匀的U形试管,横截面积S=5cm2,左侧管长l=25cm且封闭了一定质量的理想气体,右管足够长且管口开口,初始时左右两管水银面高度相等,高度h=10cm,已知周围环境温度T0=300K,大气压强p0=75cmHg。
(1)现对左侧密闭气体缓慢加热,直至两管水银面形成10cm的高度差,求密闭气体的温度T1;
(2)在保持第(1)问密闭气体温度为T1不变的情况下,从右侧管口缓慢加入水银,使得左侧管内气体恢复最初的体积,求加入的水银的体积V。(结果均保留三位有效数字)
34.在如图所示的装置中,两相同气缸A.B的长度均为,C是可在气缸内无摩擦滑动的、体积不计的活塞,D为阀门。整个装置均由导热材料制成。起初阀门关闭,A内有压强的氮气。B内有压强的氧气。阀门打开后,活塞C向右移动,最后达到平衡。求平衡后活塞C移动的距离及平衡后B中气体的压强。(假定氧气和氮气均为理想气体,连接气缸的管道体积可忽略)
35.新冠疫情期间,武汉市医疗物资紧缺,需要从北方调用大批钢瓶氧气(如图),每个钢瓶内体积为0.5m3,在北方时测得钢瓶内氧气压强为6×107Pa,温度为7℃,长途运输到武汉方舱医院检测时测得钢瓶内氧气压强为6.3×107Pa,温度为21℃。实际使用过程中,先用小钢瓶(加抽气机)缓慢分装,然后供病人使用,小钢瓶体积为0.1m3,分装后每个小钢瓶内氧气压强为4×105Pa,要求大钢瓶内压强降到2×105Pa时就停止分装,则:
(1)通过计算判断钢瓶运输途中是否漏气;
(2)一大钢瓶可分装多少小瓶供病人使用。
36.如图所示,内径相同的两U形玻璃管竖直放置在空气中,中间用细软管相连,左侧U形管顶端封闭,右侧U形管开口,用水银将部分气体A封闭在左侧U形管内,细软管内还有一部分气体.已知环境温度恒为27℃,大气压强为,稳定时,A部分气体长度为,管内各液面高度差分别为、;
①求A部分气体的压强;
②现仅给A部分气体加热,当管内气体温度升高了时,A部分气体长度为21cm,求时右侧U形管液面高度差.
37.金刚石俗称“金刚钻”,也就是我们常说的钻石,它是一种由纯碳组成的矿物,也是自然界中最坚硬的物质。已知金刚石的密度。碳原子的摩尔质量为,现有一块体积的金刚石,阿伏加德罗常数为。(计算结果保留2位有效数字)
(1)它含有多少个碳原子?
(2)假如金刚石中碳原子是紧密地堆在一起的,把金刚石中的碳原子看成球体,试估算碳原子的直径。
38.如图,一横截面积为S的圆柱形气缸竖直放置在升降机中,质量为m的活塞在缸内封闭着一定质量的理想气体,活塞上表面水平,下表面与水平面的夹角为θ。不计活塞与气缸内壁之间的摩擦,大气压强为p0,重力加速度大小为g。
(i)当升降机以加速度a竖直向上做匀加速运动时,求缸内气体的压强;
(ii)当升降机静止时,对缸内气体缓慢加热,气体吸收的热量为Q,气柱高度增加了ΔL,求加热过程中气体内能的增量。
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.BCE
【详解】
A.过程中是等压过程,根据
温度变大,体积变大,内能增加,A错误;
B.过程和过程都是等温过程,根据
则有
因为,,相同
过程是等温过程,压强变小,体积变大,外界对气体做功,过程是压强变大,体积变小,气体对外界做功,所以,过程中外界对气体做的功应大于在过程中气体对外界做的功
在过程中,等压变化,温度降低,内能减小
温度降低,体积减小,外界对气体做功,根据
即
过程中外界对气体做功
过程中,气体对外界做功
所以
在过程中外界对气体做的功等于在过程中气体对外界做的功,综合分析,整个过程气体对外界做的功大于外界对气体做的功,B正确;
C.过程中温度不变,内能不变
等温变化压强与体积成反比,从c到d体积减小,外界对气体做正功,
根据热力学第一定律
所以
所以在过程中气体向外界放出的热量等于外界对气体做的功,C正确;
D.根据压强和温度的图像,a、c两点在同一直线上过原点,即a、c两点是同一等容线上的两点,体积相等,所以气体在状态a的单位体积分子数等于在状态c的单位体积分子数,D错误;
E.过程是等温过程,温度不变,变为绝热过程后
体积变小,气体对外界做负功
根据热力学第一定律
所以
内能减小,温度降低,E正确。
故选BCE。
2.ACD
【详解】
A.扩散现象是由物质分子无规则热运动产生的分子迁移现象,可以在固体、液体、气体中产生,扩散速度与温度和物质的种类有关,故A正确;
B.在一定条件下,热量可能从低温物体传到高温物体,故B错误;
C.一定量的理想气体在等压膨胀过程中,根据理想状态的状态方程
可知气体的温度一定升高,所以内能一定增加,故C正确;
D.根据布朗运动的原因可知,液体中悬浮微粒的布朗运动是液体分子对它的撞击作用不平衡的结果,故D正确;
E.由于气体分子间距离较大,摩尔体积与分子体积的比值不等于阿伏伽德罗常数,故E错误。
故选ACD。
3.AC
【详解】
连接OE、OF,因为OF的斜率大于OE的斜率,表示
说明如果实验是从E状态→F状态,则表示外界有空气进入注射器内;如果实验是从F状态→E状态,则表示注射器内有部分空气漏了出来,故AC正确,BD错误。
故选AC。
4.BD
【详解】
A.气体由状态b变到状态a,温度降低,其内能减少,ab连线过原点,表示体积不变,A错误;
B.气体由状态a变到状态d,温度升高,其内能增加,根据
压强不变,温度升高,体积增加,B正确;
C.气体由状态d变到状态c,温度降低,其内能减少,dc连线过原点,表示体积不变,C错误;
D.气体由状态a变到状态c,温度降低,其内能减少,气体由状态a变到状态d,体积增加,气体由状态d变到状态c,体积不变,则气体由状态a变到状态c,体积增加,D正确。
故选BD。
5.AD
【详解】
气体从A到B,气体的体积减小,外界对气体做功W1>0,根据热力学第一定律有
△U1=W1+Q1
从状态A到状态C过程,气体发生等容变化,该气体对外界做功W2=0,根据热力学第一定律 有
△U2= Q2
由于两次温度的变化相同,则内能的增量相同,即
△U2=△U1
可知
Q2>Q1
选项AD正确,BC错误;
故选AD。
6.ADE
【详解】
A.气体从状态A到状态B体积不变,发生的是等容变化,气体不做功W=0,温度升高,内能增加△U>0,根据热力学第一定律△U=W+Q,知Q>0,气体吸收热量,故A正确;
B.由状态B变到状态C的过程中,温度不变,内能不变△U=0,体积变大,气体对外界做功W<0,根据热力学第一定律知Q>0,气体从外界吸收热量,故B错误;
C.气体从C到D发生等容变化,根据查理定律知p∝T,TC>TD,所以pC>pD,即C状态气体的压强大于D状态气体的压强,故C错误;
D.A点和D点在过原点的连线上,说明气体由A到D压强不变,体积增大,分子的密集程度减小,状态D温度高,分子的平均动能大,状态A和状态D压强相等,所以D状态时单位时间内与器壁单位面积碰撞的分子数比A状态少,故D正确;
E.C状态到D状态,体积不变,压强减小,温度降低,则单位时间内与器壁单位面积碰撞的分子数减少,选项E正确。
故选ADE。
7.ACD
【详解】
A.从C→B为等压变化,由公式可知,等温线2对应的气体温度比等温线1对应的气体温度高,故A正确;
B.气体从状态A变化到状态B,温度不变,则内能不变,体积增大,气体对外做功,根据热力学第一定律△U=Q+W可知,气体吸收的热量等于气体对外界做的功,故B错误;
C.气体从状态B变化到状态C,压强不变,体积增大,气体对外界做功,温度升高,内能增加,气体从状态D变化到状态A,气体吸收的热量比气体对外界做功多,故C正确;
D.气体从状态C变化到状态D,温度不变,则气体的分子平均动能不变,体积减小,则单位体积的气体分子数增大,故D正确;
E.气体从状态D变化到状态A,压强不变,温度降低,则内能减小,体积减小,则外界对气体做功,气体从状态D变化到状态A,气体放出的热量比外界对气体做功多,故E错误.
8.AD
【详解】
根据
则
则V-T图像上某点与原点连线的斜率与压强成反比。
A.因c点与原点连线的斜率小于d点与原点连线的斜率,可知c态压强大于d态压强,即从状态c到状态d的过程中,压强一直减小,选项A正确;
B.从状态d到状态a的过程中,图像上各点与原点连线的斜率增大,则压强一直减小,选项B错误;
C.从状态a到状态b的过程中,图像上各点与原点连线的斜率减小,则压强增大,选项C错误;
D.从状态b到状态c的过程中,各点与原点连线的斜率先减小后增大,则压强先增大后减小,选项D正确。
故选AD。
9.ABC
【详解】
A.根据理想气体状态方程结合图像可知,状态b、c的温度相同,故内能相等,A正确;
B.根据理想气体状态方程结合图像可知,状态a的温度比状态b、c的温度高,故状态a的内能比状态b、c的内能大,B正确;
C.由a到b的过程中,温度降低,内能减小,气体体积减小,外界对气体做功,根据热力学第一定律可知气体向外界放热,C正确;
D.据A项分析可知状态b、c的内能相等,由b到c的过程气体体积增大,气体对外界做功,根据热力学第一定律可知,整个过程从结果来看气体从外界吸热,故不可能一直向外界放热,D错误;
故选ABC。
10.C
【详解】
A.活塞缓慢地无摩擦地上升,处于平衡状态,气体压强不变 ,由盖·吕萨等压变化
可知,体积增大,温度升高。故A错误;
B.气体温度升高,内能增大,故B错误;
C.根据热力学第一定律
温度升高,大于零;体积增大,对外做功,小于零 ;故大于零,且绝对值大于的绝对值,故C正确;
D.活塞缓慢地无摩擦地上升,处于平衡状态,气体压强不变;从微观来看,虽然单位面积的分子数减少,但是温度升高,分子速度加快,碰撞更剧烈,压强不变,故D错误。
故选C。
11.D
【详解】
由理想气体状态方程有
解得
故D正确,ABC错误。
故选D。
12.C
【详解】
A.选择活塞与气缸为整体对其受力分析,受到竖直向下的总重力和弹簧向上的拉力,在升温过程中,总重力不变,所以弹簧拉力不变,即弹簧长度不变,活塞的位置不变,故A错误;
BC.气缸内的气体做等压变化,根据理想气体状态方程可以判断,温度升高时,体积增大气缸下落,所以缸体的高度变化,故C正确,B错误;
D.选择活塞与气缸为整体对其受力分析,受到竖直向下的总重力和弹簧向上的拉力,在升温过程中,总重力不变,所以弹簧拉力不变,即弹簧长度不变,故D错误.
故选C。
点睛:气缸内的气体做等压变化,根据理想气体状态方程可以判断,温度升高时,体积增大气缸下落,结合牛顿第二定律判断气缸的受力情况.
13.C
【详解】
A.当P增大时,根据气态方程
可知气体的体积不一定减小,还与温度的变化情况有关,所以单位体积内的分子数不一定增大,故A错误;
B.当T减小时,根据气态方程
可知气体的体积不一定减小,还与压强的变化情况有关,所以单位体积内的分子数不一定增大,故B错误;
CD.当增大时,根据气态方程
可知气体的体积一定减小,所以单位体积内的分子数一定增大,故C正确,D错误。
故选C。
14.D
【详解】
AB.过程由图可知为等温变化,气体内能不变,根据玻意耳定律可知,当压强p增大时,体积V减小,可知外界对气体做功,根据热力学第一定律,由于内能不变,可知过程气体放出热量,故AB错误;
C.由图可知为等容变化,为等压变化,过程中气体温度升高,根据盖—吕萨克定律可知体积变大,由于压强不变,温度升高,气体分子平均速率增大,则气体分子在单位时间内撞击单位面积容器壁的次数减少,故C错误;
D.由于a、c两个状态体积相同,则过程气体体积的变化量与过程气体体积的变化量相同,而过程气体压强不变,过程气体压强增大,根据可知,过程气体对外界做的功小于过程外界对气体做的功,故D正确。
故选D。
15.C
【详解】
由查理定律知
代入数据
解得
故选C。
16.C
【详解】
AB:假设液柱不动,则A、B两部分气体发生等容变化.对气体A:;则得 即;对气体B,同理可得:.据题意初始温度相同,,升高相同的温度, 且,则,液柱将向上移动.故AB两项错误.
CD:系统稳定后,液注的上下表面的高度差将变大,液注上下表面的压强差变大,即系统稳定后,;又,所以.故C项正确,D项错误.
【点睛】
本题可采取假设法,假设气体的体积不变,根据等容变化判断出上下气体的压强变化量,从而判断出水银柱的移动方向.
17.C
【详解】
设降温后水银柱不动,则两段空气柱均为等容变化,初始状态左、右两端压强相等,即
对左端
则
同理,对右端
所以
即右侧压强降低得比左侧多,故水银柱向右移动,故C正确,ABD错误。
18.(1)42℃;(2)1:4
【详解】
(1)由查理定律
得
T2=315K=42℃
(2)车胎内原来气体,由
解得
相同压强条件下,新充入气体与车胎内原来气体的质量比等于体积比
19.个
【详解】
因为,带入得
所以
所以气体的质量
所以分子数
个个
20.(1);(2);(3)
【详解】
(1)过程为等压膨胀,所以气体对外做功为
(2)过程为绝热过程,气体对外做功为
(3)则气体对外界做的总功为
21.(i)T2=250K(t2=-23℃) (ii)h=L2-L3=11 cm
【解析】
【详解】
(ⅰ)初态,气体的温度为T1=300K,体积V1=120 cm·S,压强
物块离开桌面时,气体的温度为T2,体积V2=L2·S=110cm·S
压强
由理想气体状态方程:
解得 T2=250K(t2=-23℃)
(ⅱ)温度降低到-48℃,T3=225K,体积V3=L3·S
由盖 吕萨克定律
解得 L3=99cm
即物块离桌面的高度为h=L2-L3=11 cm
22.85 cmHg ,318 K
【详解】
设玻璃管的横截面积为S,初态时,管内气体的温度为T1=306 K,体积为V1=51S cm3,压强为p1=p0+h=80cmHg.
当水银面与管口相平时,水银柱高为H,则管内气体的体积为V2=(57 H)S cm3,压强为p2=p0+H=(76+H)cmHg.
由玻意耳定律得 p1V1=p2V2
代入数据,得 H2+19H 252=0
解得:H=9cm
所以p2=85 cmHg
新注入水银柱的高度为Δh=H-4cm=5cm
23.①温度为T1时气体的压强;
②此时气体的温度.
【详解】
①气体对外做功
由热力学第一定律得
解得
②设活塞回到原位置时,气体的温度为T2
则初态
由气态方程
解得
本题考查气体内能和气体状态,改变内能的两种形式做功和热传递,分析气体状态时主要是找到初末状态的参量,列方程求解
24.(1)55cm (2) 45.75oC
【解析】试题分析:①加入水银柱后空气柱下降,气体做等压变化;由盖-吕萨克定律可求得气柱的长度L;②加入水银柱的长度.温度升高,封闭气体体积增大,水银柱上升,当电路恰好接通时,报警器开始报警;此时空气柱长度,以封闭空气柱为研究对象,根据等压变化规律求出温度.
①设试管的横截面积为S,在温度从57℃缓慢至27℃的过程中,封闭气体做等压变化,由盖-吕萨克定律有:
上式中:;
代入解得:L=55cm;
②当环境温度为57℃时,封闭气体的压强为:;
当报警装置再次恰好报警时,封闭气柱的长度为:
此时封闭气体的压强为
由理想气体状态方程有:
解得t=45.75℃;
25.(1);(2)50J;(3)
【详解】
(1)由A到B是等温变化:由玻意耳定律知
解得
(2)由A到B是等温变化,理想气体内能不变,
则由热力学第一定律知,吸收的热量
(3)由B到C为等压变化
由盖吕萨克定律
解得
26.(1);(2)
【详解】
(1)以气缸为研究对象,由平衡条件得
解得
(2)以整体为研究对象,加速度a为
以气缸为研究对象
解得:。
27.(1)78 ℃;(2)11.75 cm
【详解】
(1) 设截面积为S,取左管中气体为研究对象,初状态
p1=1atm=76cmHg
T1=t1+273K=304K
V1=l1S=(8cm)·S
因为左管水银面下降1cm,右管水银面一定上升1cm,则左右两管高度差为2cm,因而末状态
p2=(76+2)cmHg=78cmHg
V2=(9cm)·S
由=,代入数据解得
T2=351K
从而知
t2=78℃
(2)在78℃情况下,气柱长从9cm减小到8cm,体积减小,压强一定增大,即压强大于78cmHg,故要往右管加水银。由,且V1=V3,T2=T3有:
p3==76×cmHg=87.75cmHg
故应在右管加水银柱
(87.75-76)cm=11.75cm
28.(1)369K;(2)40cm;(3)
【详解】
(1)由于水银总体积保持不变,设水银全部进入细管水银长度为x,则
得
,
从状态1到状态2由理想气体状态方程,代入数据
(2)从状态2到状态3经历等压过程,设水银下表面离开粗细接口处的高度为,则
所以水银下表面离开玻璃管底部的距离
(3)根据对应的压强和体积的数据作出p-V图象如图所示
29.(1);(2)
【详解】
(1) 设气缸横截面积为;D刚好被触发时,到缸底的距离为,根据玻意耳定律得
带入数据解得
(2)此过程为等容变化,根据查理定律得
带入数据解得
30.(1)1.5T1;(2)1.8p0
【详解】
(1)活塞下方的气体在活塞从开始运动到活塞刚碰到玻璃管顶部的过程为等压变化
初态:体积V1,温度T1
末态:体积V2=V1+0.5V1,温度T2
根据盖﹣吕萨克定律得
解得
(2)活塞下方的气体温度从1.5T到1.8T的过程为等容变化
初态:压强,温度T2=1.5T1
末态:压强p3,温度T3=1.8T1
根据查理定律得
解得
31.(i) (ii) 8
【详解】
试题分析:气体发生等容变化,由查理定律可求解足球内部的空气压强;可采用等效法,把足球内的气体还原为p0状态,把此时气体和要打入的气体为研究对象利用玻意耳定律可求次数.
(i)足球内气体经历等容变化过程,,
由查理定律得
得
(ii)设足球容积为V2、压强为p2的空气等温变化为压强为p0的室外空气时的体积为V3,需要补充的气体体积为V,打气次数为N
由玻意耳定律得
解得N=8
32.(1);(2)4
【详解】
(1)篮球内气体做等容变化,由
得
(2)设室温下原来篮球内气体的体积为,由
解得
所以
33.(1)453K;(2)192cm3
【详解】
(1)设加热后左侧的气体压强为p1,体积为V1,由题目已知有
由理想气体状态方程有
其中
解得
(2)保持理想气体温度不变,加入水银,可视为等温过程,设加入水银后理想气体的压强为p2,此时左右两管的水银面高度差为,有
解得
加入的水银的体积
【答案】,
【解析】
试题分析:平衡后,气缸A.B内的压强相等,设气缸的横截面积为S,取A气缸内的氮气为研究对象,由玻意耳定律有:
取气缸B内的氧气为研究对象,由玻意耳定律有:
解得:,。
考点:理想气体的状态方程
【名师点睛】两部分气体都是发生等温变化,应用玻意耳定律对A.B两部分气体列方程,然后求出距离与压强;本题是两部分气体连接问题,分析清楚气体状态变化过程,应用玻意耳定律即可正确解题。
35.(1)没有漏气;(2)785
【详解】
(1)钢瓶的容积一定,从北方到武汉对钢瓶内气体,若成立,则气体的质量一定,即没有发生漏气。
在北方
在武汉
可见成立,即钢瓶在运输途中没有发生漏气。
(2) 在武汉时,设大瓶内氧气由P2、V2等温变化为不分装时的状态P3、V3,则P2=6.3×107Pa,V2=0.5m3,P3=2×105Pa。
根据P2V2=P3V3,得V3=157.5m3。
可用于分装小瓶的氧气P4=2×105Pa,V4=(157.5-0.5)m3=157 m3
分装成小钢瓶的氧气P5=4×105Pa,V5=n V,其中小钢瓶体积为V=0.1 m3。
根据P4V4=P5V5,得n=785。
即一大钢瓶氧气可分装785小瓶。
36.(1) (2)
【详解】
①设左侧A部分气体压强为p1,软管内气体压强为p2,由图中液面的高度关系可知,
,,解得;
②由理想气体状态方程有 ,解得;
由于空气柱长度增加1cm,则水银柱向右侧移动1cm,因此液面高度差,,解得;
37.(1);(2)。
【详解】
(1)金刚石的质量
碳的物质的量
金刚石所含碳原子数
个
(2)一个碳原子的体积
把金刚石中的碳原子看成球体,则由公式可得碳原子直径为
38.(i);(ii)
【详解】
(ⅰ)活塞受力如图所示。设缸内气体的压强为p
缸内气体对活塞的压力大小为
在竖直方向,根据牛顿第二定律有
解得
(ⅱ)加热过程中缸内气体等压膨胀,活塞处于平衡状态,设缸内气体的压强为,内能增量为,由力的平衡条件有
可得
气体克服外界做的功为
由热力学第一定律有
联立求解得
答案第1页,共2页
答案第1页,共2页
一、多选题
1.一定量的理想气体从状态a开始,经历等温或等压过程ab、bc、cd、da回到原状态,其p-T图象如图所示,其中对角线ac的延长线过原点O。下列判断正确的是( )
A.在过程da中气体的内能增加,体积减小
B.在整个过程气体对外界做的功大于外界对气体做的功
C.在过程cd中气体向外界放出的热量等于外界对气体做的功
D.气体在状态a的单位体积分子数大于在状态c的单位体积分子数
E.若将过程ab改为绝热过程且压强变化相同,则状态的温度小于状态b的温度
2.下列说法正确的是( )
A.扩散现象在气体、液体和固体中都能发生
B.热量不可能从低温物体传到高温物体
C.一定质量的某种理想气体在等压膨胀的过程中,内能一定增加
D.布朗运动是液体分子对液体中悬浮微粒的撞击作用不平衡的结果
E.某气体的摩尔体积为V,每个分子的体积为,则阿伏加德罗常数可表示为
3.某同学用带有刻度的注射器做验证玻意耳定律的实验,温度计表明在图中的图线可以得出( )
A.如果实验是从E状态→F状态,则表示外界有空气进入注射器内
B.如果实验是从E状态→F状态,则表示注射器内有部分空气漏了出来
C.如果实验是从F状态→E状态,则表示注射器内有部分空气漏了出来
D.如果实验是从F状态→E状态,则表示外界有空气进入注射器内
4.如图所示为一定质量的理想气体在不同体积时的两条等容线,a、b、c、d表示四个不同状态,则( )
A.气体由状态b变到状态a,其内能减少,体积增加
B.气体由状态a变到状态d,其内能增加,体积增加
C.气体由状态d变到状态c,其内能增加,体积不变
D.气体由状态a变到状态c,其内能减少,体积增加
5.一定质量的理想气体状态变化过程如图所示,第1种变化是从状态A到状态B,第2种变化是从状态A到状态C,(AC的反向延长线过原点O),比较气体的两种状态变化过程中:( )
A.气体从状态A到状态C过程气体吸收热量较多
B.气体从状态A到状态B过程气体吸收热量较多
C.气体从状态A到状态B过程内能增加较多
D.两个过程中气体内能增加量相同
6.封闭在汽缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度T关系如图所示,O、A、D三点在同一直线上。则________。
A.由状态A变到状态B过程中,气体吸收热量
B.由状态B变到状态C过程中,气体从外界吸收热量,内能增加
C.C状态气体的压强小于D状态气体的压强
D.D状态时单位时间内与器壁单位面积碰撞的分子数比A状态少
E.C状态到D状态,单位时间内与器壁单位面积碰撞的分子数减少
7.如图所示,为一定质量的理想气体发生状态变化的p-V图象,图线1、2是两条等温线,A、B是等温线1上的两点,C、D是等温线2上的两点,图线AD、BC均与V轴平行,则下列说法正确的是( )
A.等温线2对应的气体温度比等温线1对应的气体温度高
B.气体从状态A变化到状态B,气体吸收的热量比气体对外界做功多
C.气体从状态B变化到状态C,气体吸收的热量比气体对外界做功多
D.气体从状态C变化到状态D,单位体积的气体分子数增大,但气体分子的平均动能不变
E.气体从状态D变化到状态A,气体放出的热量比外界对气体做功少,气体内能增加
8.如图所示为一定质量的理想气体沿箭头所示的方向发生状态变化的过程,则关于该气体压强变化的下列说法中正确的是( )
A.从状态c到状态d的过程中,压强一直减小
B.从状态d到状态a的过程中,压强一直增大
C.从状态a到状态b的过程中,压强先增大后减小
D.从状态b到状态c的过程中,压强先增大后减小
9.一定质量的理想气体状态变化如图所示,则( )
A.状态b、c的内能相等
B.状态a的内能比状态b、c的内能大
C.由a到b的过程中气体向外界放热
D.由b到c的过程中气体一直向外界放热
二、单选题
10.如图,绝热的容器内封闭一定质量的理想气体(不考虑分子势能,外界大气压恒定),用电阻丝对其加热时,绝热活塞缓慢地无摩擦地上升,下列正确的是( )
A.活塞上升,气体体积增大,温度降低
B.气体从电阻丝吸收热量,气体又对外做功,气体内能可能不变
C.气体从电阻丝吸收的热量一定大于气体对外做功
D.气体体积增大,单位时间内打到器壁单位面积的分子数减少,气体压强一定减小
11.回热式制冷机是一种深低温设备,制冷极限约50K,某台设备工作时,一定量的氦气(可视为理想气体)缓慢经历如图所示的四个过程:从状态A到B和C到D是等温过程,温度分别为t1=27℃和t2=-133℃;从状态B到C和D到A是等容过程,体积分别为V0和5V0,则状态B与D的压强之比是( )
A.7∶3 B.15∶7 C.133∶27 D.75∶7
12.如图所示,一导热性能良好的气缸吊在弹簧下,缸内被活塞封住一定质量的气体(不计活塞与缸壁摩擦),当温度升高到某一数值时,变化了的量有:( )
A.活塞高度h B.气体压强p C.缸体高度H D.弹簧长度L
13.一定质量的某种理想气体的压强为,热力学温度为,单位体积内的气体分子数为,则( )
A.增大,一定增大
B.减小,一定增大
C.增大时,一定增大
D.增大时,一定减小
14.一定质量的理想气体按的顺序经历一系列状态变化,其图像如图所示。图中线段与纵轴平行,线段与纵轴垂直。气体在状态变化过程中下列叙述正确的是( )
A.过程气体体积增加
B.过程气体不放热也不吸热
C.过程气体分子在单位时间内撞击单位面积容器壁的次数增加
D.过程气体对外界做的功小于过程外界对气体做的功
15.一个密闭的钢管内装有空气,在温度为20℃时,压强为1atm,若温度上升到80℃,管内空气的压强约为( )
A.4atm B. C.1.2atm D.
16.图示为竖直放置、上细下粗、两端封闭的玻璃细管,水银柱将气体分隔成A、B两部分,初始温度相同.缓缓加热气体,使A、B升高相同温度,系统稳定后,A、B两部分气体对液面压力的变化量分别为△FA和△FB,压强变化量分别为△pA和△pB.则( )
A.水银柱向下移动了一段距离
B.水银柱不发生移动
C.△FA<△FB
D.△pA=△pB
17.两端封闭且内径均匀的直玻璃管,水平放置,如图所示,左、右两端空气柱的体积关系为,温度均为20℃,现将右端空气柱降为0℃,左端空气柱降为10℃,则管中水银柱将( )
A.不动 B.向左移动
C.向右移动 D.无法确定是否移动
三、解答题
18.胎压监测装置是在汽车行驶过程中对轮胎气压进行实时自动监测的装置。一辆长期停放的汽车,某车胎内气体温度为27℃,胎压监测装置显示该车胎实际气压为200kPa,考虑到胎压不足,司机驾驶车辆到汽车修理店充气,行驶一段路程到汽车修理店后,胎压监刻装置显示该车胎胎压为210kPa,工作人员为该车胎充气,充气完毕后汽车停放一段时间,胎内气体温度恢复到27℃时,胎压监刻装置显示该车胎胎压为250kPa,若不考虑轮胎内气体体积变化。求:
(1)车胎胎压为210kPa时轮胎内气体温度为多少摄氏度;
(2)新充入气体与车胎内原来气体的质量比。
19.某氮气气弹簧撑开时,腔体内气体的体积约为,压强为,温度为27℃。在压强为、0℃时氮气的密度为。已知氮气的摩尔质量为,阿伏伽德罗常数为,请估算腔体内气体的分子数(计算结果保留一位有效数字)
20.如图所示,一定质量理想气体经历A→B的等压过程,B→C的绝热过程(气体与外界无热量交换),其中B→C过程中内能减少900J。求A→B→C过程中气体对外界做的总功。
(1)过程气体对外做的功;
(2)过程气体对外做的功;
(3)A→B→C过程中气体对外界做的总功。
21.如图所示,水平面上固定着开口向上的汽缸,质量m=5 kg、横截面积S =50 cm2 的活塞密封了一定质量的理想气体,一根轻绳一端系在活塞上,另一端跨过两个定滑轮连着一根劲度系数k=500 N/m的竖直轻弹簧,弹簧的下端系一质量M=5 kg的物块。开始时,缸内气体的温度t1 =27℃,活塞到缸底的距离L1 =120cm,弹簧恰好处于原长。已知大气压强p0 =1.0 ×105Pa,不计一切摩擦,现使缸内气体缓慢冷却,求
(i)物块恰好离开桌面时,缸内气体的温度t2;
(ii)缸内气体的温度降低到-48℃时,物块离桌面的高度h。
22.如图所示,在长为l=57cm的一端封闭、另端开口向上的竖直玻璃管内,用4cm高的水银柱封闭着51cm长的理想气体,管内外气体的温度均为33℃.
(1)现将水银徐徐注入管中,直到水银面与管口相平,此时管中气体的压强为多少
(2)接着(1)中问题缓慢对玻璃管加热升温至多少时,管中刚好只剩下4cm高的水银柱 (大气压强为p0=76cmHg)
23.如图所示,一圆柱形绝热气缸竖直放置,通过绝热活塞封闭着一定质量的理想气体.活塞的质量为m,横截面积为S,与容器底部相距h.现通过电热丝缓慢加热气体,当气体的温度为T1时活塞上升了h.已知大气压强为p0.重力加速度为g,不计活塞与气缸间摩擦.
①求温度为T1时气体的压强;
②现停止对气体加热,同时在活塞上缓慢添加砂粒,当添加砂粒的质量为m0时,活塞恰好回到原来位置,求此时气体的温度.
24.某同学设计的简易火灾报警装置如图所示,竖直固定、上端开口的试管中装有高h=20cm的水银.其下方封闭有一段气柱。当环境温度为57℃时,电路恰好接通,电铃D发出报警声。取绝对零度为-273℃。
①若环境温度缓慢降至27℃时,水银柱下降了△L=5cm,试求环境温度为57℃时,试管内封闭气柱的长度L;
②若使环境温度降低,并且往玻璃管内注入高△h=4 cm的水银时,报警装置恰好再次报警,求此时的环境温度t(已知大气压强p0= 76 cmHg)。
25.一定质量理想气体的体积V与热力学温度T的关系如图所示,气体在状态A的压强为pA=1.5p0,温度TA=1.5T0,线段AB与V轴平行,BC的延长线过原点。求:
(1)B点的压强pB:
(2)气体从状态A变化到状态B的过程中,对外界做的功为50J,则该过程中吸收的热量Q;
(3)状态C的温度Tc。
26.如图所示,倾角为的光滑斜面上有一固定挡板O,现有一质量为M的气缸,气缸内用质量为m的活塞封闭有一定质量的理想气体,活塞与气缸间光滑,活塞横截面为S,现将活塞用细绳固定在挡板O上处于静止状态。(已知外界大气压强为P0)求:
(1)气缸内的气体压强P1;
(2)若将绳子剪断,气缸与活塞保持相对静止一起沿斜面向下做匀加速直线运动,试计算气缸内的气体压强P2。
27.如图所示,粗细均匀的、一端封闭一端开口的U形玻璃管,当t1=31 ℃、大气压强p0=1atm时,两管水银面相平,这时左管被封闭气柱长l1=8 cm。求:
(1)当温度t2等于多少时,左管气柱长l2为9 cm
(2)当温度达到上问中温度t2时,为使左管气柱长l3为8 cm,则应在右管再加多高的水银柱?
28.如图(甲)所示为一下粗上细且上端开口的薄壁玻璃管,管内有一部分水银封住密闭气体,上管足够长,图中大小截面积分别为S1=2cm2、S2=1cm2,粗细管内水银长度分别为h1=h2=2cm,封闭气体长度为L=22cm。大气压强为p0=76cmHg,气体初始温度为57。求:
(1)若缓慢升高气体温度,升高至多少开尔文方可将所有水银全部挤入细管内;
(2)若温度升高至492K,液柱下端离开玻璃管底部的距离;
(3)在图(乙)中作出全过程的p-V图象。
29.如图,圆柱形导热气缸长,缸内用活塞(质量和厚度均不计)密闭了一定质量的理想气体,缸底装有一个触发器D,当缸内压强达到时,D被触发,不计活塞与缸壁的摩擦。初始时,活塞位于缸口处,环境温度,压强。
(1)若环境温度不变,缓慢向下推活塞,求D刚好被触发时,到缸底的距离;
(2)若活塞固定在缸口位置,缓慢升高环境温度,求D刚好被触发时的环境温度。
30.如图所示,一根粗细均匀、内壁光滑、竖直放置的薄壁玻璃管下端密封,上端封闭但留有一气孔与外界大气相连。管内下端有被活塞封住的一定量的理想气体,设外界大气压强为p0,活塞因重力而产生的压强为0.5p0,开始时,气体温度为T1,活塞上方的气体的体积为0.5V1,活塞下方玻璃管的容积为V1。现对活塞下端密封的气体缓慢加热。求:
(1)活塞刚碰到玻璃管顶部时,气体的温度;
(2)当气体温度达到1.8T1时,气体的压强。
31.冬季南北方气温差异很大,若在某一时刻海南三亚地区的气温为27℃,而此时黑龙江北部的漠河地区气温为-33℃.在这一时刻有一个容积为2.5 L的足球放在了三亚,足球内部的空气压强为2.0×105Pa,假设足球的容积不变,热力学温度与摄氏温度的关系为T=t+273 K,室外空气压强声p0=1.0×105 Pa.
(i)若足球此时放在漠河,求足球内部的空气压强;
(ii)若足球此时放在漠河,并用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压强相同的气体打进球内,求打多少次才能让足球内部空气压强恢复到2.0×10 5 Pa (打气过程中假设足球内的气体温度不变)
32.在室温为17℃时给一个篮球充气使其压强达到,室内外大气压强均为,设在下述整个过程中篮球体积不变。
(1)在球场比赛时温度升高到37℃,这时球内压强有多大?(结果保留两位有效数字)
(2)由于漏气,当篮球内气体的压强变为,温度仍为17℃时,求球内剩下的空气与漏出空气的质量比值。
33.如图所示,竖直放置的粗细均匀的U形试管,横截面积S=5cm2,左侧管长l=25cm且封闭了一定质量的理想气体,右管足够长且管口开口,初始时左右两管水银面高度相等,高度h=10cm,已知周围环境温度T0=300K,大气压强p0=75cmHg。
(1)现对左侧密闭气体缓慢加热,直至两管水银面形成10cm的高度差,求密闭气体的温度T1;
(2)在保持第(1)问密闭气体温度为T1不变的情况下,从右侧管口缓慢加入水银,使得左侧管内气体恢复最初的体积,求加入的水银的体积V。(结果均保留三位有效数字)
34.在如图所示的装置中,两相同气缸A.B的长度均为,C是可在气缸内无摩擦滑动的、体积不计的活塞,D为阀门。整个装置均由导热材料制成。起初阀门关闭,A内有压强的氮气。B内有压强的氧气。阀门打开后,活塞C向右移动,最后达到平衡。求平衡后活塞C移动的距离及平衡后B中气体的压强。(假定氧气和氮气均为理想气体,连接气缸的管道体积可忽略)
35.新冠疫情期间,武汉市医疗物资紧缺,需要从北方调用大批钢瓶氧气(如图),每个钢瓶内体积为0.5m3,在北方时测得钢瓶内氧气压强为6×107Pa,温度为7℃,长途运输到武汉方舱医院检测时测得钢瓶内氧气压强为6.3×107Pa,温度为21℃。实际使用过程中,先用小钢瓶(加抽气机)缓慢分装,然后供病人使用,小钢瓶体积为0.1m3,分装后每个小钢瓶内氧气压强为4×105Pa,要求大钢瓶内压强降到2×105Pa时就停止分装,则:
(1)通过计算判断钢瓶运输途中是否漏气;
(2)一大钢瓶可分装多少小瓶供病人使用。
36.如图所示,内径相同的两U形玻璃管竖直放置在空气中,中间用细软管相连,左侧U形管顶端封闭,右侧U形管开口,用水银将部分气体A封闭在左侧U形管内,细软管内还有一部分气体.已知环境温度恒为27℃,大气压强为,稳定时,A部分气体长度为,管内各液面高度差分别为、;
①求A部分气体的压强;
②现仅给A部分气体加热,当管内气体温度升高了时,A部分气体长度为21cm,求时右侧U形管液面高度差.
37.金刚石俗称“金刚钻”,也就是我们常说的钻石,它是一种由纯碳组成的矿物,也是自然界中最坚硬的物质。已知金刚石的密度。碳原子的摩尔质量为,现有一块体积的金刚石,阿伏加德罗常数为。(计算结果保留2位有效数字)
(1)它含有多少个碳原子?
(2)假如金刚石中碳原子是紧密地堆在一起的,把金刚石中的碳原子看成球体,试估算碳原子的直径。
38.如图,一横截面积为S的圆柱形气缸竖直放置在升降机中,质量为m的活塞在缸内封闭着一定质量的理想气体,活塞上表面水平,下表面与水平面的夹角为θ。不计活塞与气缸内壁之间的摩擦,大气压强为p0,重力加速度大小为g。
(i)当升降机以加速度a竖直向上做匀加速运动时,求缸内气体的压强;
(ii)当升降机静止时,对缸内气体缓慢加热,气体吸收的热量为Q,气柱高度增加了ΔL,求加热过程中气体内能的增量。
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.BCE
【详解】
A.过程中是等压过程,根据
温度变大,体积变大,内能增加,A错误;
B.过程和过程都是等温过程,根据
则有
因为,,相同
过程是等温过程,压强变小,体积变大,外界对气体做功,过程是压强变大,体积变小,气体对外界做功,所以,过程中外界对气体做的功应大于在过程中气体对外界做的功
在过程中,等压变化,温度降低,内能减小
温度降低,体积减小,外界对气体做功,根据
即
过程中外界对气体做功
过程中,气体对外界做功
所以
在过程中外界对气体做的功等于在过程中气体对外界做的功,综合分析,整个过程气体对外界做的功大于外界对气体做的功,B正确;
C.过程中温度不变,内能不变
等温变化压强与体积成反比,从c到d体积减小,外界对气体做正功,
根据热力学第一定律
所以
所以在过程中气体向外界放出的热量等于外界对气体做的功,C正确;
D.根据压强和温度的图像,a、c两点在同一直线上过原点,即a、c两点是同一等容线上的两点,体积相等,所以气体在状态a的单位体积分子数等于在状态c的单位体积分子数,D错误;
E.过程是等温过程,温度不变,变为绝热过程后
体积变小,气体对外界做负功
根据热力学第一定律
所以
内能减小,温度降低,E正确。
故选BCE。
2.ACD
【详解】
A.扩散现象是由物质分子无规则热运动产生的分子迁移现象,可以在固体、液体、气体中产生,扩散速度与温度和物质的种类有关,故A正确;
B.在一定条件下,热量可能从低温物体传到高温物体,故B错误;
C.一定量的理想气体在等压膨胀过程中,根据理想状态的状态方程
可知气体的温度一定升高,所以内能一定增加,故C正确;
D.根据布朗运动的原因可知,液体中悬浮微粒的布朗运动是液体分子对它的撞击作用不平衡的结果,故D正确;
E.由于气体分子间距离较大,摩尔体积与分子体积的比值不等于阿伏伽德罗常数,故E错误。
故选ACD。
3.AC
【详解】
连接OE、OF,因为OF的斜率大于OE的斜率,表示
说明如果实验是从E状态→F状态,则表示外界有空气进入注射器内;如果实验是从F状态→E状态,则表示注射器内有部分空气漏了出来,故AC正确,BD错误。
故选AC。
4.BD
【详解】
A.气体由状态b变到状态a,温度降低,其内能减少,ab连线过原点,表示体积不变,A错误;
B.气体由状态a变到状态d,温度升高,其内能增加,根据
压强不变,温度升高,体积增加,B正确;
C.气体由状态d变到状态c,温度降低,其内能减少,dc连线过原点,表示体积不变,C错误;
D.气体由状态a变到状态c,温度降低,其内能减少,气体由状态a变到状态d,体积增加,气体由状态d变到状态c,体积不变,则气体由状态a变到状态c,体积增加,D正确。
故选BD。
5.AD
【详解】
气体从A到B,气体的体积减小,外界对气体做功W1>0,根据热力学第一定律有
△U1=W1+Q1
从状态A到状态C过程,气体发生等容变化,该气体对外界做功W2=0,根据热力学第一定律 有
△U2= Q2
由于两次温度的变化相同,则内能的增量相同,即
△U2=△U1
可知
Q2>Q1
选项AD正确,BC错误;
故选AD。
6.ADE
【详解】
A.气体从状态A到状态B体积不变,发生的是等容变化,气体不做功W=0,温度升高,内能增加△U>0,根据热力学第一定律△U=W+Q,知Q>0,气体吸收热量,故A正确;
B.由状态B变到状态C的过程中,温度不变,内能不变△U=0,体积变大,气体对外界做功W<0,根据热力学第一定律知Q>0,气体从外界吸收热量,故B错误;
C.气体从C到D发生等容变化,根据查理定律知p∝T,TC>TD,所以pC>pD,即C状态气体的压强大于D状态气体的压强,故C错误;
D.A点和D点在过原点的连线上,说明气体由A到D压强不变,体积增大,分子的密集程度减小,状态D温度高,分子的平均动能大,状态A和状态D压强相等,所以D状态时单位时间内与器壁单位面积碰撞的分子数比A状态少,故D正确;
E.C状态到D状态,体积不变,压强减小,温度降低,则单位时间内与器壁单位面积碰撞的分子数减少,选项E正确。
故选ADE。
7.ACD
【详解】
A.从C→B为等压变化,由公式可知,等温线2对应的气体温度比等温线1对应的气体温度高,故A正确;
B.气体从状态A变化到状态B,温度不变,则内能不变,体积增大,气体对外做功,根据热力学第一定律△U=Q+W可知,气体吸收的热量等于气体对外界做的功,故B错误;
C.气体从状态B变化到状态C,压强不变,体积增大,气体对外界做功,温度升高,内能增加,气体从状态D变化到状态A,气体吸收的热量比气体对外界做功多,故C正确;
D.气体从状态C变化到状态D,温度不变,则气体的分子平均动能不变,体积减小,则单位体积的气体分子数增大,故D正确;
E.气体从状态D变化到状态A,压强不变,温度降低,则内能减小,体积减小,则外界对气体做功,气体从状态D变化到状态A,气体放出的热量比外界对气体做功多,故E错误.
8.AD
【详解】
根据
则
则V-T图像上某点与原点连线的斜率与压强成反比。
A.因c点与原点连线的斜率小于d点与原点连线的斜率,可知c态压强大于d态压强,即从状态c到状态d的过程中,压强一直减小,选项A正确;
B.从状态d到状态a的过程中,图像上各点与原点连线的斜率增大,则压强一直减小,选项B错误;
C.从状态a到状态b的过程中,图像上各点与原点连线的斜率减小,则压强增大,选项C错误;
D.从状态b到状态c的过程中,各点与原点连线的斜率先减小后增大,则压强先增大后减小,选项D正确。
故选AD。
9.ABC
【详解】
A.根据理想气体状态方程结合图像可知,状态b、c的温度相同,故内能相等,A正确;
B.根据理想气体状态方程结合图像可知,状态a的温度比状态b、c的温度高,故状态a的内能比状态b、c的内能大,B正确;
C.由a到b的过程中,温度降低,内能减小,气体体积减小,外界对气体做功,根据热力学第一定律可知气体向外界放热,C正确;
D.据A项分析可知状态b、c的内能相等,由b到c的过程气体体积增大,气体对外界做功,根据热力学第一定律可知,整个过程从结果来看气体从外界吸热,故不可能一直向外界放热,D错误;
故选ABC。
10.C
【详解】
A.活塞缓慢地无摩擦地上升,处于平衡状态,气体压强不变 ,由盖·吕萨等压变化
可知,体积增大,温度升高。故A错误;
B.气体温度升高,内能增大,故B错误;
C.根据热力学第一定律
温度升高,大于零;体积增大,对外做功,小于零 ;故大于零,且绝对值大于的绝对值,故C正确;
D.活塞缓慢地无摩擦地上升,处于平衡状态,气体压强不变;从微观来看,虽然单位面积的分子数减少,但是温度升高,分子速度加快,碰撞更剧烈,压强不变,故D错误。
故选C。
11.D
【详解】
由理想气体状态方程有
解得
故D正确,ABC错误。
故选D。
12.C
【详解】
A.选择活塞与气缸为整体对其受力分析,受到竖直向下的总重力和弹簧向上的拉力,在升温过程中,总重力不变,所以弹簧拉力不变,即弹簧长度不变,活塞的位置不变,故A错误;
BC.气缸内的气体做等压变化,根据理想气体状态方程可以判断,温度升高时,体积增大气缸下落,所以缸体的高度变化,故C正确,B错误;
D.选择活塞与气缸为整体对其受力分析,受到竖直向下的总重力和弹簧向上的拉力,在升温过程中,总重力不变,所以弹簧拉力不变,即弹簧长度不变,故D错误.
故选C。
点睛:气缸内的气体做等压变化,根据理想气体状态方程可以判断,温度升高时,体积增大气缸下落,结合牛顿第二定律判断气缸的受力情况.
13.C
【详解】
A.当P增大时,根据气态方程
可知气体的体积不一定减小,还与温度的变化情况有关,所以单位体积内的分子数不一定增大,故A错误;
B.当T减小时,根据气态方程
可知气体的体积不一定减小,还与压强的变化情况有关,所以单位体积内的分子数不一定增大,故B错误;
CD.当增大时,根据气态方程
可知气体的体积一定减小,所以单位体积内的分子数一定增大,故C正确,D错误。
故选C。
14.D
【详解】
AB.过程由图可知为等温变化,气体内能不变,根据玻意耳定律可知,当压强p增大时,体积V减小,可知外界对气体做功,根据热力学第一定律,由于内能不变,可知过程气体放出热量,故AB错误;
C.由图可知为等容变化,为等压变化,过程中气体温度升高,根据盖—吕萨克定律可知体积变大,由于压强不变,温度升高,气体分子平均速率增大,则气体分子在单位时间内撞击单位面积容器壁的次数减少,故C错误;
D.由于a、c两个状态体积相同,则过程气体体积的变化量与过程气体体积的变化量相同,而过程气体压强不变,过程气体压强增大,根据可知,过程气体对外界做的功小于过程外界对气体做的功,故D正确。
故选D。
15.C
【详解】
由查理定律知
代入数据
解得
故选C。
16.C
【详解】
AB:假设液柱不动,则A、B两部分气体发生等容变化.对气体A:;则得 即;对气体B,同理可得:.据题意初始温度相同,,升高相同的温度, 且,则,液柱将向上移动.故AB两项错误.
CD:系统稳定后,液注的上下表面的高度差将变大,液注上下表面的压强差变大,即系统稳定后,;又,所以.故C项正确,D项错误.
【点睛】
本题可采取假设法,假设气体的体积不变,根据等容变化判断出上下气体的压强变化量,从而判断出水银柱的移动方向.
17.C
【详解】
设降温后水银柱不动,则两段空气柱均为等容变化,初始状态左、右两端压强相等,即
对左端
则
同理,对右端
所以
即右侧压强降低得比左侧多,故水银柱向右移动,故C正确,ABD错误。
18.(1)42℃;(2)1:4
【详解】
(1)由查理定律
得
T2=315K=42℃
(2)车胎内原来气体,由
解得
相同压强条件下,新充入气体与车胎内原来气体的质量比等于体积比
19.个
【详解】
因为,带入得
所以
所以气体的质量
所以分子数
个个
20.(1);(2);(3)
【详解】
(1)过程为等压膨胀,所以气体对外做功为
(2)过程为绝热过程,气体对外做功为
(3)则气体对外界做的总功为
21.(i)T2=250K(t2=-23℃) (ii)h=L2-L3=11 cm
【解析】
【详解】
(ⅰ)初态,气体的温度为T1=300K,体积V1=120 cm·S,压强
物块离开桌面时,气体的温度为T2,体积V2=L2·S=110cm·S
压强
由理想气体状态方程:
解得 T2=250K(t2=-23℃)
(ⅱ)温度降低到-48℃,T3=225K,体积V3=L3·S
由盖 吕萨克定律
解得 L3=99cm
即物块离桌面的高度为h=L2-L3=11 cm
22.85 cmHg ,318 K
【详解】
设玻璃管的横截面积为S,初态时,管内气体的温度为T1=306 K,体积为V1=51S cm3,压强为p1=p0+h=80cmHg.
当水银面与管口相平时,水银柱高为H,则管内气体的体积为V2=(57 H)S cm3,压强为p2=p0+H=(76+H)cmHg.
由玻意耳定律得 p1V1=p2V2
代入数据,得 H2+19H 252=0
解得:H=9cm
所以p2=85 cmHg
新注入水银柱的高度为Δh=H-4cm=5cm
23.①温度为T1时气体的压强;
②此时气体的温度.
【详解】
①气体对外做功
由热力学第一定律得
解得
②设活塞回到原位置时,气体的温度为T2
则初态
由气态方程
解得
本题考查气体内能和气体状态,改变内能的两种形式做功和热传递,分析气体状态时主要是找到初末状态的参量,列方程求解
24.(1)55cm (2) 45.75oC
【解析】试题分析:①加入水银柱后空气柱下降,气体做等压变化;由盖-吕萨克定律可求得气柱的长度L;②加入水银柱的长度.温度升高,封闭气体体积增大,水银柱上升,当电路恰好接通时,报警器开始报警;此时空气柱长度,以封闭空气柱为研究对象,根据等压变化规律求出温度.
①设试管的横截面积为S,在温度从57℃缓慢至27℃的过程中,封闭气体做等压变化,由盖-吕萨克定律有:
上式中:;
代入解得:L=55cm;
②当环境温度为57℃时,封闭气体的压强为:;
当报警装置再次恰好报警时,封闭气柱的长度为:
此时封闭气体的压强为
由理想气体状态方程有:
解得t=45.75℃;
25.(1);(2)50J;(3)
【详解】
(1)由A到B是等温变化:由玻意耳定律知
解得
(2)由A到B是等温变化,理想气体内能不变,
则由热力学第一定律知,吸收的热量
(3)由B到C为等压变化
由盖吕萨克定律
解得
26.(1);(2)
【详解】
(1)以气缸为研究对象,由平衡条件得
解得
(2)以整体为研究对象,加速度a为
以气缸为研究对象
解得:。
27.(1)78 ℃;(2)11.75 cm
【详解】
(1) 设截面积为S,取左管中气体为研究对象,初状态
p1=1atm=76cmHg
T1=t1+273K=304K
V1=l1S=(8cm)·S
因为左管水银面下降1cm,右管水银面一定上升1cm,则左右两管高度差为2cm,因而末状态
p2=(76+2)cmHg=78cmHg
V2=(9cm)·S
由=,代入数据解得
T2=351K
从而知
t2=78℃
(2)在78℃情况下,气柱长从9cm减小到8cm,体积减小,压强一定增大,即压强大于78cmHg,故要往右管加水银。由,且V1=V3,T2=T3有:
p3==76×cmHg=87.75cmHg
故应在右管加水银柱
(87.75-76)cm=11.75cm
28.(1)369K;(2)40cm;(3)
【详解】
(1)由于水银总体积保持不变,设水银全部进入细管水银长度为x,则
得
,
从状态1到状态2由理想气体状态方程,代入数据
(2)从状态2到状态3经历等压过程,设水银下表面离开粗细接口处的高度为,则
所以水银下表面离开玻璃管底部的距离
(3)根据对应的压强和体积的数据作出p-V图象如图所示
29.(1);(2)
【详解】
(1) 设气缸横截面积为;D刚好被触发时,到缸底的距离为,根据玻意耳定律得
带入数据解得
(2)此过程为等容变化,根据查理定律得
带入数据解得
30.(1)1.5T1;(2)1.8p0
【详解】
(1)活塞下方的气体在活塞从开始运动到活塞刚碰到玻璃管顶部的过程为等压变化
初态:体积V1,温度T1
末态:体积V2=V1+0.5V1,温度T2
根据盖﹣吕萨克定律得
解得
(2)活塞下方的气体温度从1.5T到1.8T的过程为等容变化
初态:压强,温度T2=1.5T1
末态:压强p3,温度T3=1.8T1
根据查理定律得
解得
31.(i) (ii) 8
【详解】
试题分析:气体发生等容变化,由查理定律可求解足球内部的空气压强;可采用等效法,把足球内的气体还原为p0状态,把此时气体和要打入的气体为研究对象利用玻意耳定律可求次数.
(i)足球内气体经历等容变化过程,,
由查理定律得
得
(ii)设足球容积为V2、压强为p2的空气等温变化为压强为p0的室外空气时的体积为V3,需要补充的气体体积为V,打气次数为N
由玻意耳定律得
解得N=8
32.(1);(2)4
【详解】
(1)篮球内气体做等容变化,由
得
(2)设室温下原来篮球内气体的体积为,由
解得
所以
33.(1)453K;(2)192cm3
【详解】
(1)设加热后左侧的气体压强为p1,体积为V1,由题目已知有
由理想气体状态方程有
其中
解得
(2)保持理想气体温度不变,加入水银,可视为等温过程,设加入水银后理想气体的压强为p2,此时左右两管的水银面高度差为,有
解得
加入的水银的体积
【答案】,
【解析】
试题分析:平衡后,气缸A.B内的压强相等,设气缸的横截面积为S,取A气缸内的氮气为研究对象,由玻意耳定律有:
取气缸B内的氧气为研究对象,由玻意耳定律有:
解得:,。
考点:理想气体的状态方程
【名师点睛】两部分气体都是发生等温变化,应用玻意耳定律对A.B两部分气体列方程,然后求出距离与压强;本题是两部分气体连接问题,分析清楚气体状态变化过程,应用玻意耳定律即可正确解题。
35.(1)没有漏气;(2)785
【详解】
(1)钢瓶的容积一定,从北方到武汉对钢瓶内气体,若成立,则气体的质量一定,即没有发生漏气。
在北方
在武汉
可见成立,即钢瓶在运输途中没有发生漏气。
(2) 在武汉时,设大瓶内氧气由P2、V2等温变化为不分装时的状态P3、V3,则P2=6.3×107Pa,V2=0.5m3,P3=2×105Pa。
根据P2V2=P3V3,得V3=157.5m3。
可用于分装小瓶的氧气P4=2×105Pa,V4=(157.5-0.5)m3=157 m3
分装成小钢瓶的氧气P5=4×105Pa,V5=n V,其中小钢瓶体积为V=0.1 m3。
根据P4V4=P5V5,得n=785。
即一大钢瓶氧气可分装785小瓶。
36.(1) (2)
【详解】
①设左侧A部分气体压强为p1,软管内气体压强为p2,由图中液面的高度关系可知,
,,解得;
②由理想气体状态方程有 ,解得;
由于空气柱长度增加1cm,则水银柱向右侧移动1cm,因此液面高度差,,解得;
37.(1);(2)。
【详解】
(1)金刚石的质量
碳的物质的量
金刚石所含碳原子数
个
(2)一个碳原子的体积
把金刚石中的碳原子看成球体,则由公式可得碳原子直径为
38.(i);(ii)
【详解】
(ⅰ)活塞受力如图所示。设缸内气体的压强为p
缸内气体对活塞的压力大小为
在竖直方向,根据牛顿第二定律有
解得
(ⅱ)加热过程中缸内气体等压膨胀,活塞处于平衡状态,设缸内气体的压强为,内能增量为,由力的平衡条件有
可得
气体克服外界做的功为
由热力学第一定律有
联立求解得
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
