16.2.2二次根式的除法 课件(共31页)
文档属性
| 名称 | 16.2.2二次根式的除法 课件(共31页) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
16.2 二次根式的乘除
人教版八下数学
第2课时 二次根式的除法
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
二次根式的乘法法则是什么内容?
化简二次根式的一般步骤是什么?
复习引入
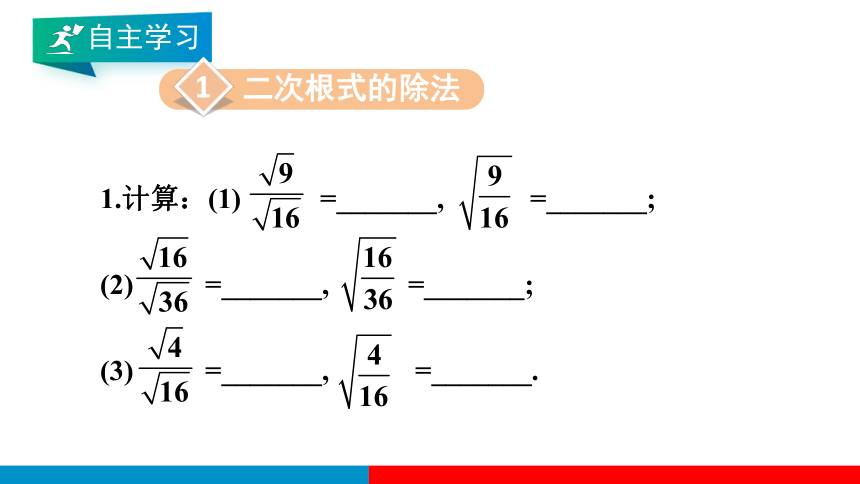
二次根式的除法
1
1.计算:(1) =_______, =_______;
(2) =_______, =_______;
(3) =_______, =_______.
自主学习
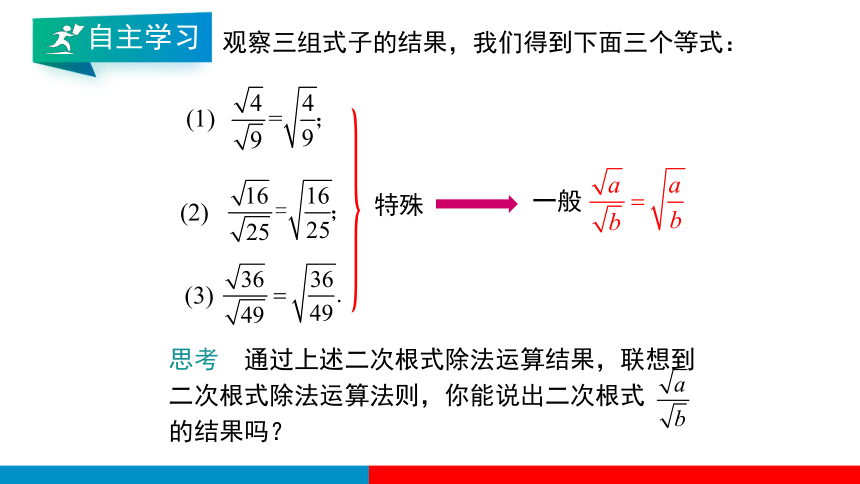
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
思考 通过上述二次根式除法运算结果,联想到二次根式除法运算法则,你能说出二次根式 的结果吗?
特殊
一般
自主学习
法则:两个二次根式相除,把被开方数相除,根指数不变,即: (a≥0,b>0).
特别提醒
●法则中的被开方数a,b既可以是数,也可以是式子,但都必须是非负的且b不为0;若b=0,则式子无意义.
文字叙述:
算术平方根的商等于被开方数商的算术平方根.
自主学习
例 1
计算:
(1) ;(2)
解:(1)
(2)
典例分析
1.计算:
(1) ;(2) ;
(3) ;(4) .
(1) 3; (2)
(3) (4)2a.
解:
课堂练习
2. 成立的条件是( )
A.a≠1 B.a≥1且a≠3
C.a>1 D.a≥3
3.计算 的结果是( )
A. B. C. D.
D
C
课堂练习
商的算术平方根
2
把 反过来,就得到 (a≥0,
b>0) ,利用它可以进行二次根式的化简.
特别提醒
●商的算术平方根的性质的实质是逆用二次根式的除法法则.
●利用商的算术平方根的性质可以把被开方数中含有分母的二次根式化成被开方数不含分母的二次根式.
自主学习
例2
化简:(1) (2)
解:(1)
(2)
典例分析
计算:(1) (2) (3)
例 3
典例分析
解:(1)解法1:
解法2:
(2)
(3)
典例分析
总 结
分母有理化一般经历如下三步:
“一移”,即将分子、分母中能开得尽方的因数(式)移
到根号外;
“二乘”,即将分子、分母同乘分母的有理化因数(式);
“三化”,即化简计算.
1.下列各式计算正确的是( )
A. B.
C. D.
2 若 ,则a的取值范围是( )
A.a≤0 B.a<0 C.a>0 D.0C
D
课堂练习
最简二次根式
3
定义:如果一个二次根式满足以下两个条件,
那么这个二次根式叫做最简二次根式:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
简记为:一根号无分母,分母无根号;二不能再开方.
自主学习
归 纳
最简二次根式必须满足:
(1)被开方数不含分母,也就是被开方数必须是整
数(式);
(2)被开方数中每个因数(式)的指数都小于根指数2,
即每个因数(式)的指数都是1.
自主学习
在下列各式中,哪些是最简二次根式?哪些不是?对不是最简二次根式的进行化简.
解:只有(3)是最简二次根式;
例 4
典例分析
设长方形的面积为S,相邻两边长分别为a,b.
已知S = ,b= ,求 a.
例 5
解:因为S=ab,所以
典例分析
1.把下列二次根式化成最简二次根式:
(1) (2) (3) (4)
(1) ; (2) ;
(3) (4)
解:
课堂练习
2.设长方形的面积为S,相邻两边长分别为a,b.
已知S=16,b= ,求a.
解:由题意得S=ab,所以
课堂练习
3.【中考·荆州】下列根式是最简二次根式的是( )
A. B.
C. D.
C
课堂练习
二次根式的
除法
1.二次根式的除法:
两个二次根式相除,把被开方数相除,根指
数不变,即: (a≥0,b>0).
2.最简二次根式:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
1.计算:
解:
1.计算:
解:
备选习题
2.化简:
解:
备选习题
3.化简:
解:
备选习题
3.化简:
解:
备选习题
3化简:
解:
备选习题
https://www.21cnjy.com/help/help_extract.php
16.2 二次根式的乘除
人教版八下数学
第2课时 二次根式的除法
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
二次根式的乘法法则是什么内容?
化简二次根式的一般步骤是什么?
复习引入
二次根式的除法
1
1.计算:(1) =_______, =_______;
(2) =_______, =_______;
(3) =_______, =_______.
自主学习
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
思考 通过上述二次根式除法运算结果,联想到二次根式除法运算法则,你能说出二次根式 的结果吗?
特殊
一般
自主学习
法则:两个二次根式相除,把被开方数相除,根指数不变,即: (a≥0,b>0).
特别提醒
●法则中的被开方数a,b既可以是数,也可以是式子,但都必须是非负的且b不为0;若b=0,则式子无意义.
文字叙述:
算术平方根的商等于被开方数商的算术平方根.
自主学习
例 1
计算:
(1) ;(2)
解:(1)
(2)
典例分析
1.计算:
(1) ;(2) ;
(3) ;(4) .
(1) 3; (2)
(3) (4)2a.
解:
课堂练习
2. 成立的条件是( )
A.a≠1 B.a≥1且a≠3
C.a>1 D.a≥3
3.计算 的结果是( )
A. B. C. D.
D
C
课堂练习
商的算术平方根
2
把 反过来,就得到 (a≥0,
b>0) ,利用它可以进行二次根式的化简.
特别提醒
●商的算术平方根的性质的实质是逆用二次根式的除法法则.
●利用商的算术平方根的性质可以把被开方数中含有分母的二次根式化成被开方数不含分母的二次根式.
自主学习
例2
化简:(1) (2)
解:(1)
(2)
典例分析
计算:(1) (2) (3)
例 3
典例分析
解:(1)解法1:
解法2:
(2)
(3)
典例分析
总 结
分母有理化一般经历如下三步:
“一移”,即将分子、分母中能开得尽方的因数(式)移
到根号外;
“二乘”,即将分子、分母同乘分母的有理化因数(式);
“三化”,即化简计算.
1.下列各式计算正确的是( )
A. B.
C. D.
2 若 ,则a的取值范围是( )
A.a≤0 B.a<0 C.a>0 D.0
D
课堂练习
最简二次根式
3
定义:如果一个二次根式满足以下两个条件,
那么这个二次根式叫做最简二次根式:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
简记为:一根号无分母,分母无根号;二不能再开方.
自主学习
归 纳
最简二次根式必须满足:
(1)被开方数不含分母,也就是被开方数必须是整
数(式);
(2)被开方数中每个因数(式)的指数都小于根指数2,
即每个因数(式)的指数都是1.
自主学习
在下列各式中,哪些是最简二次根式?哪些不是?对不是最简二次根式的进行化简.
解:只有(3)是最简二次根式;
例 4
典例分析
设长方形的面积为S,相邻两边长分别为a,b.
已知S = ,b= ,求 a.
例 5
解:因为S=ab,所以
典例分析
1.把下列二次根式化成最简二次根式:
(1) (2) (3) (4)
(1) ; (2) ;
(3) (4)
解:
课堂练习
2.设长方形的面积为S,相邻两边长分别为a,b.
已知S=16,b= ,求a.
解:由题意得S=ab,所以
课堂练习
3.【中考·荆州】下列根式是最简二次根式的是( )
A. B.
C. D.
C
课堂练习
二次根式的
除法
1.二次根式的除法:
两个二次根式相除,把被开方数相除,根指
数不变,即: (a≥0,b>0).
2.最简二次根式:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
1.计算:
解:
1.计算:
解:
备选习题
2.化简:
解:
备选习题
3.化简:
解:
备选习题
3.化简:
解:
备选习题
3化简:
解:
备选习题
https://www.21cnjy.com/help/help_extract.php
