4.3.3 余角和补角
图片预览







文档简介
课件21张PPT。4.3 角(第5课时)
4.3.3 余角和补角七年级数学上册
(人教版2012年秋季使用)
几何图形初步 课件说明 本节课主要学习余角、补角概念,余角、补角的性质,方位角.
余角和补角是在学习了角的度量及角的比较与运算的基础上,对角的数量关系作进一步探讨,在后面学习对顶角相等及平行线的判定和性质时即将用到,并为今后证明角的相等提供一种依据和方法.另外教材在此已开始对学生提出“简单说理”的要求,为以后推理证明题作准备.方位角的知识学生在小学就有所了解,但根据题意画出方位角以及运用方位角的知识确定点的位置是学生不熟悉的.方位角的知识在“解直角三角形”等内容有广泛的应用,并且为今后学习平面直角坐标系、极坐标等知识奠定基础.课件说明学习目标:
(1)认识一个角的余角和补角,并会求一个角的余角和补角.
(2)掌握余角和补角的性质,并能用它解决相关问题.
(3)通过余角、补角性质的推导和应用,初步掌握图形语言与符号语言之间的相互转化.初步接触和体会演绎推理的方法和表述,进一步提高学生的抽象概括能力,识图能力,发展空间观念.
(4)认识并理解方位角,能画出方位角所表示方向的射线,并会在实际问题中应用它确定一个物体的位置,进一步体会数形结合的方法.课件说明学习重点:
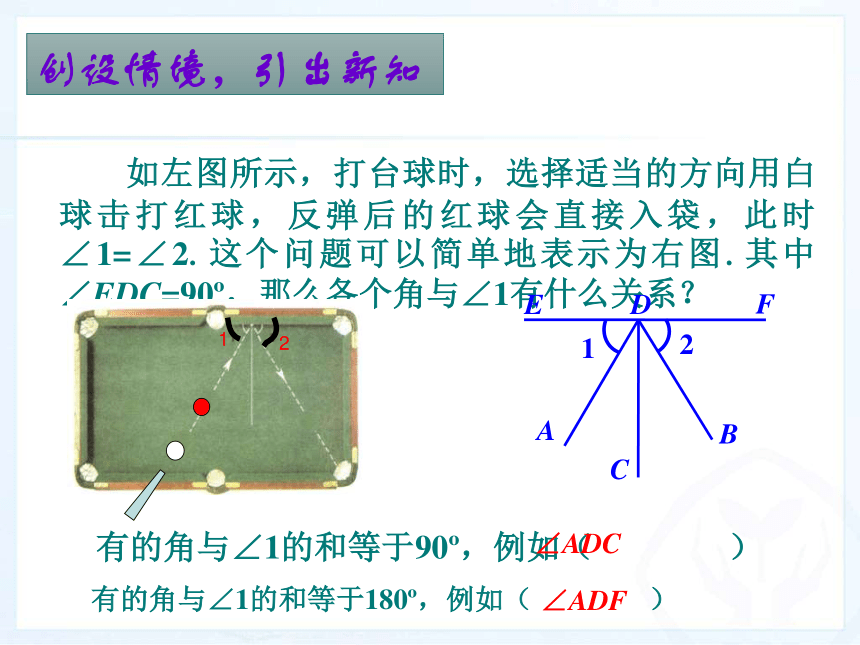
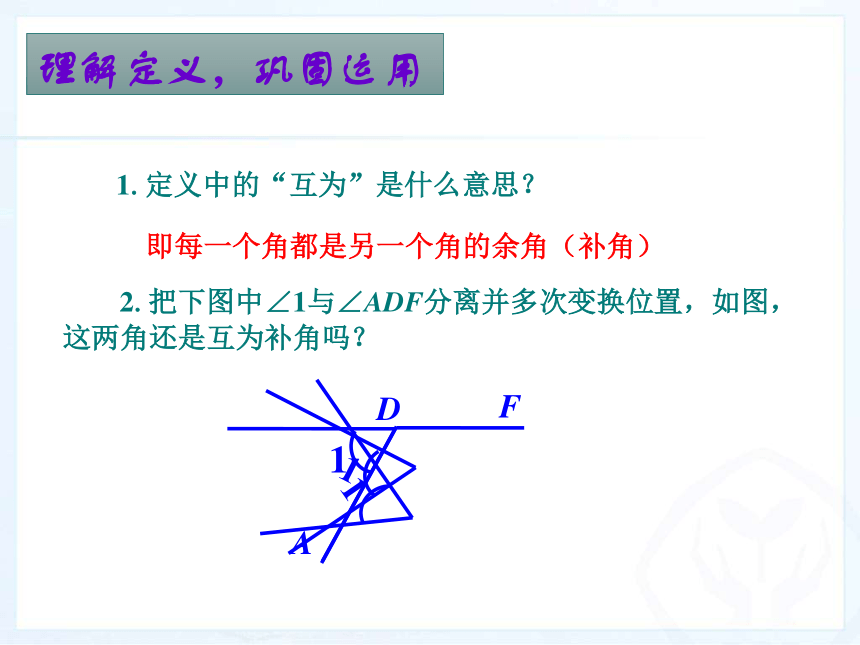
互余、互补的概念及其性质.本课件以PPT的形式呈现,直观地展示了画方位角的过程,使学生印象深刻.创设情境,引出新知 如左图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2.这个问题可以简单地表示为右图.其中∠EDC=90o,那么各个角与∠1有什么关系? 有的角与∠1的和等于90o,例如( ) ∠ADC 有的角与∠1的和等于180o,例如( ) ∠ADF创设情境,引出新知 如果两个角的和等于90o(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角. 如果两个角的和等于180o(平角),就说这两个角互为补角,即其中一个角是另一个角的补角. 1.定义中的“互为”是什么意思? 2.把下图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?理解定义,巩固运用即每一个角都是另一个角的余角(补角)理解定义,巩固运用(1)若∠1与∠2互补,则∠1+∠2=______. (2) ∠1=90o-∠2,则∠1与∠2的关系为___________.180°互为余角(3)图中给出的各角中,哪些互为余角?哪些互为补角? (1)已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?推导性质,理解运用 由∠1与∠2和∠3都互为补角,
那么 ∠2=180o-∠1,
∠3=180o-∠1,所以∠2=∠3.
(2)已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,那么∠2和∠4 相等吗?为什么? 由∠1与∠2互补,得∠1+∠2=180o,
所以 ∠2=180o-∠1. 由∠3与∠4互补,得∠3+∠4=180o, 所以∠4=180o-∠3.又因为∠1=∠3,180o-∠1=180o-∠3,所以∠2=∠4.推导性质,理解运用等角 的余角相等.等角 的补角相等.对于余角是否也有类似性质?(同角)(同角) (1)若∠1与∠2互余,∠2与∠3互余, 则_____=______,根据是________ .
(2)若∠3与∠4互补,∠6与∠5互补,且∠3=∠6, 则_____=______,根据是__________.同角的余角相等等角的补角相等∠1∠3∠4∠5推导性质,理解运用例 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?推导性质,理解运用推导性质,理解运用所以∠COD +∠COE= ∠AOC+ ∠BOC 解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.又因为射线OD和射线OE分别平分∠AOC∠BOC,= (∠AOC+ ∠BOC)=90°所以, ∠COD 和∠COE互为余角,同理, ∠AOD +∠BOE,
∠AOD +∠COE ,
∠COD +∠BOE也互为余角. 有时以正北、正南方向为基准,描述物体运动的方向. 表示方向的角(方位角)在航行、测绘等工作中经常用到.推导性质,理解运用例 如图,货轮O在航行过程中,发现灯塔A在它南偏东60o的方向上,同时,在它北偏东40o、南偏西10o、西北(即北偏西45o)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.● A40° B C10°45° D推导性质,理解运用强化练习,巩固提高 (1)一个角是70o39′,求它的余角和补角.
(2)∠α的补角是它的3倍,∠α是多少度?
(3)一个角是钝角,它的一半是什么角?它的余角是90o-70o39′=19o21′,
它的补角是180o-70o39′=109o21′.由180o- ∠α=3 ∠α,解得∠α=45o.锐角课堂小结,自我完善∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等.同角或等角的补角相等.拓展延伸,布置作业 1.课本第140页 7题,8题,第141页11题,12题,13题.
2.∠α的余角是它的3倍,∠α是多少度?拓展延伸,布置作业 3.(选做题)一个角的余角比这个角的补角的 还小10°,求这个角的余角及这个角的补角的度数.(用两种方法求解)
4.3.3 余角和补角七年级数学上册
(人教版2012年秋季使用)
几何图形初步 课件说明 本节课主要学习余角、补角概念,余角、补角的性质,方位角.
余角和补角是在学习了角的度量及角的比较与运算的基础上,对角的数量关系作进一步探讨,在后面学习对顶角相等及平行线的判定和性质时即将用到,并为今后证明角的相等提供一种依据和方法.另外教材在此已开始对学生提出“简单说理”的要求,为以后推理证明题作准备.方位角的知识学生在小学就有所了解,但根据题意画出方位角以及运用方位角的知识确定点的位置是学生不熟悉的.方位角的知识在“解直角三角形”等内容有广泛的应用,并且为今后学习平面直角坐标系、极坐标等知识奠定基础.课件说明学习目标:
(1)认识一个角的余角和补角,并会求一个角的余角和补角.
(2)掌握余角和补角的性质,并能用它解决相关问题.
(3)通过余角、补角性质的推导和应用,初步掌握图形语言与符号语言之间的相互转化.初步接触和体会演绎推理的方法和表述,进一步提高学生的抽象概括能力,识图能力,发展空间观念.
(4)认识并理解方位角,能画出方位角所表示方向的射线,并会在实际问题中应用它确定一个物体的位置,进一步体会数形结合的方法.课件说明学习重点:
互余、互补的概念及其性质.本课件以PPT的形式呈现,直观地展示了画方位角的过程,使学生印象深刻.创设情境,引出新知 如左图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2.这个问题可以简单地表示为右图.其中∠EDC=90o,那么各个角与∠1有什么关系? 有的角与∠1的和等于90o,例如( ) ∠ADC 有的角与∠1的和等于180o,例如( ) ∠ADF创设情境,引出新知 如果两个角的和等于90o(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角. 如果两个角的和等于180o(平角),就说这两个角互为补角,即其中一个角是另一个角的补角. 1.定义中的“互为”是什么意思? 2.把下图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?理解定义,巩固运用即每一个角都是另一个角的余角(补角)理解定义,巩固运用(1)若∠1与∠2互补,则∠1+∠2=______. (2) ∠1=90o-∠2,则∠1与∠2的关系为___________.180°互为余角(3)图中给出的各角中,哪些互为余角?哪些互为补角? (1)已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?推导性质,理解运用 由∠1与∠2和∠3都互为补角,
那么 ∠2=180o-∠1,
∠3=180o-∠1,所以∠2=∠3.
(2)已知∠1与∠2互补,∠3与∠4互补.若∠1=∠3,那么∠2和∠4 相等吗?为什么? 由∠1与∠2互补,得∠1+∠2=180o,
所以 ∠2=180o-∠1. 由∠3与∠4互补,得∠3+∠4=180o, 所以∠4=180o-∠3.又因为∠1=∠3,180o-∠1=180o-∠3,所以∠2=∠4.推导性质,理解运用等角 的余角相等.等角 的补角相等.对于余角是否也有类似性质?(同角)(同角) (1)若∠1与∠2互余,∠2与∠3互余, 则_____=______,根据是________ .
(2)若∠3与∠4互补,∠6与∠5互补,且∠3=∠6, 则_____=______,根据是__________.同角的余角相等等角的补角相等∠1∠3∠4∠5推导性质,理解运用例 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?推导性质,理解运用推导性质,理解运用所以∠COD +∠COE= ∠AOC+ ∠BOC 解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.又因为射线OD和射线OE分别平分∠AOC∠BOC,= (∠AOC+ ∠BOC)=90°所以, ∠COD 和∠COE互为余角,同理, ∠AOD +∠BOE,
∠AOD +∠COE ,
∠COD +∠BOE也互为余角. 有时以正北、正南方向为基准,描述物体运动的方向. 表示方向的角(方位角)在航行、测绘等工作中经常用到.推导性质,理解运用例 如图,货轮O在航行过程中,发现灯塔A在它南偏东60o的方向上,同时,在它北偏东40o、南偏西10o、西北(即北偏西45o)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.● A40° B C10°45° D推导性质,理解运用强化练习,巩固提高 (1)一个角是70o39′,求它的余角和补角.
(2)∠α的补角是它的3倍,∠α是多少度?
(3)一个角是钝角,它的一半是什么角?它的余角是90o-70o39′=19o21′,
它的补角是180o-70o39′=109o21′.由180o- ∠α=3 ∠α,解得∠α=45o.锐角课堂小结,自我完善∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等.同角或等角的补角相等.拓展延伸,布置作业 1.课本第140页 7题,8题,第141页11题,12题,13题.
2.∠α的余角是它的3倍,∠α是多少度?拓展延伸,布置作业 3.(选做题)一个角的余角比这个角的补角的 还小10°,求这个角的余角及这个角的补角的度数.(用两种方法求解)
