2021-2022学年北师大版九年级数学上册4.5相似三角形判定定理的证明自主提升训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.5相似三角形判定定理的证明自主提升训练(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 423.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 23:54:32 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学上册《4-5相似三角形判定定理的证明》
自主提升训练(附答案)
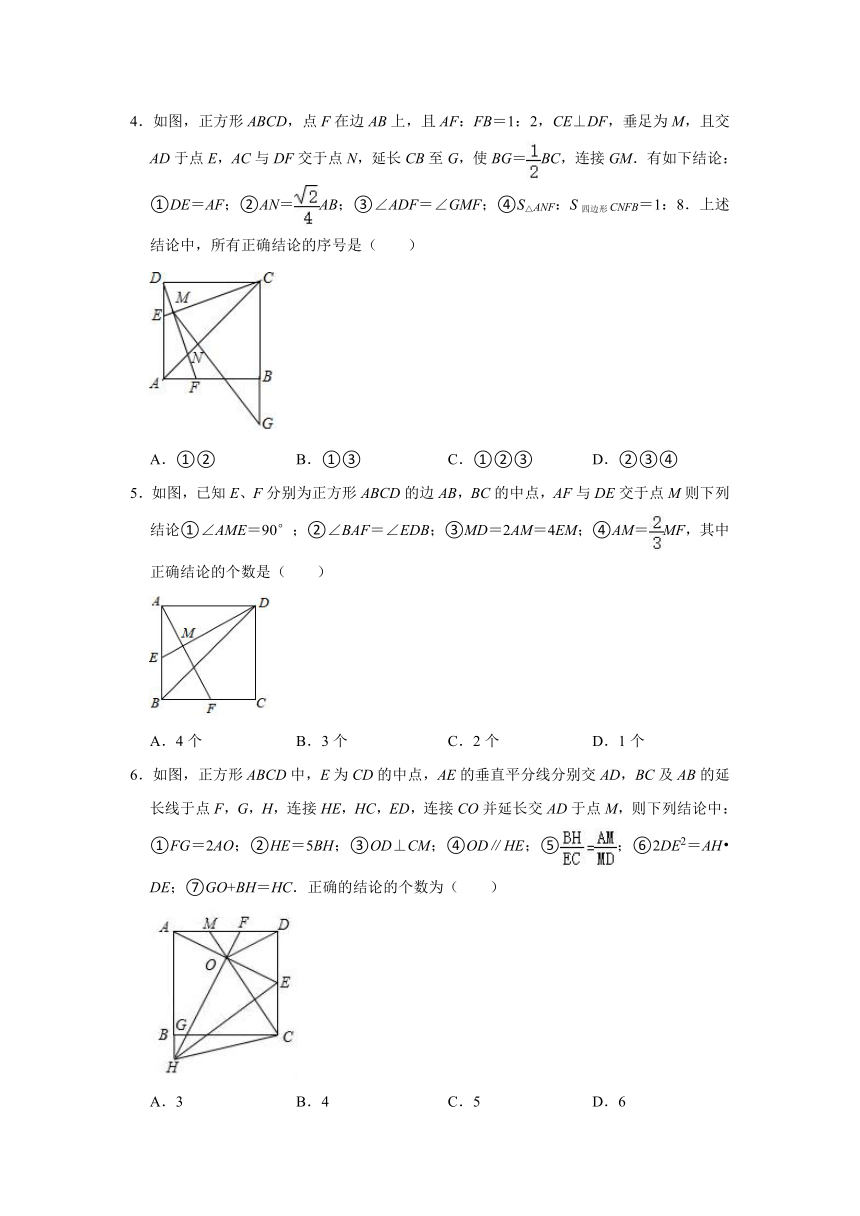
1.如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,延长BG交CD于点F,延长CG交BD于点H,交AB于N下列结论:
①DE=CN;②=;③S△DEC=3S△BNH;④∠BGN=45°;⑤GN+EG=BG;
其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
2.如图,正方形ABCD中,E为BC中点,连接AE,DF⊥AE于点F,连接CF,FG⊥CF交AD于点G,下列结论:①CF=CD;②G为AD中点;③△DCF∽△AGF;④=,其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:①BH垂直平分AE;②AH=DF;③DF=DE;④∠AEF=45°;⑤S四边形EFHG=S△DEF+S△AGH,其中正确的结论有( )个.
A.2 B.3 C.4 D.5
4.如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=BC,连接GM.有如下结论:①DE=AF;②AN=AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.②③④
5.如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M则下列结论①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM;④AM=MF,其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
6.如图,正方形ABCD中,E为CD的中点,AE的垂直平分线分别交AD,BC及AB的延长线于点F,G,H,连接HE,HC,ED,连接CO并延长交AD于点M,则下列结论中:①FG=2AO;②HE=5BH;③OD⊥CM;④OD∥HE;⑤;⑥2DE2=AH DE;⑦GO+BH=HC.正确的结论的个数为( )
A.3 B.4 C.5 D.6
7.如图,在正方形ABCD中,△ABF和△BCE是等边三角形,边AF与CE交于点H,BE的延长线交AD于点P,AF的延长线交CD于点G,连接DH.给出下列结论:
①AE=DH;
②4S△AEB=S正方形ABCD;
③DH2=HF AD;
④5EP=3EH.
其中正确的是( )
A.①③ B.①②③ C.①③④ D.①②③④
8.如图所示,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N,下列结论:①AF⊥BG;②BN=NF;③=;④S四边形CGNF=S四边形ANGD.其中正确的结论的序号是( )
A.①③ B.②④ C.①② D.③④
9.如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.给出以下结论:①△AED≌△BFA;②DE﹣BF=EF;③△BGF∽△DAE;④DE﹣BG=FG.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①∠DEC=∠AEB;②CF⊥DE;③AF=BF;④=,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
11.如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连接EN、EF,有以下结论:①△ABM∽△NEM;②△AEN是等腰直角三角形;③当AE=AF时,;④BE+DF=EF;⑤若点F是DC的中点,则CE=CB,其中正确的个数是( )
A.2 B.3 C.4 D.5
12.如图,在四边形ABCD中,AD∥BC,∠DBC=45°,BD=2,BC=3,则的最小值为 .
13.如图,在△ABC中,点D是AB边上的一点,且AD=3BD,连接CD并取CD的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6,则AB的长为 .
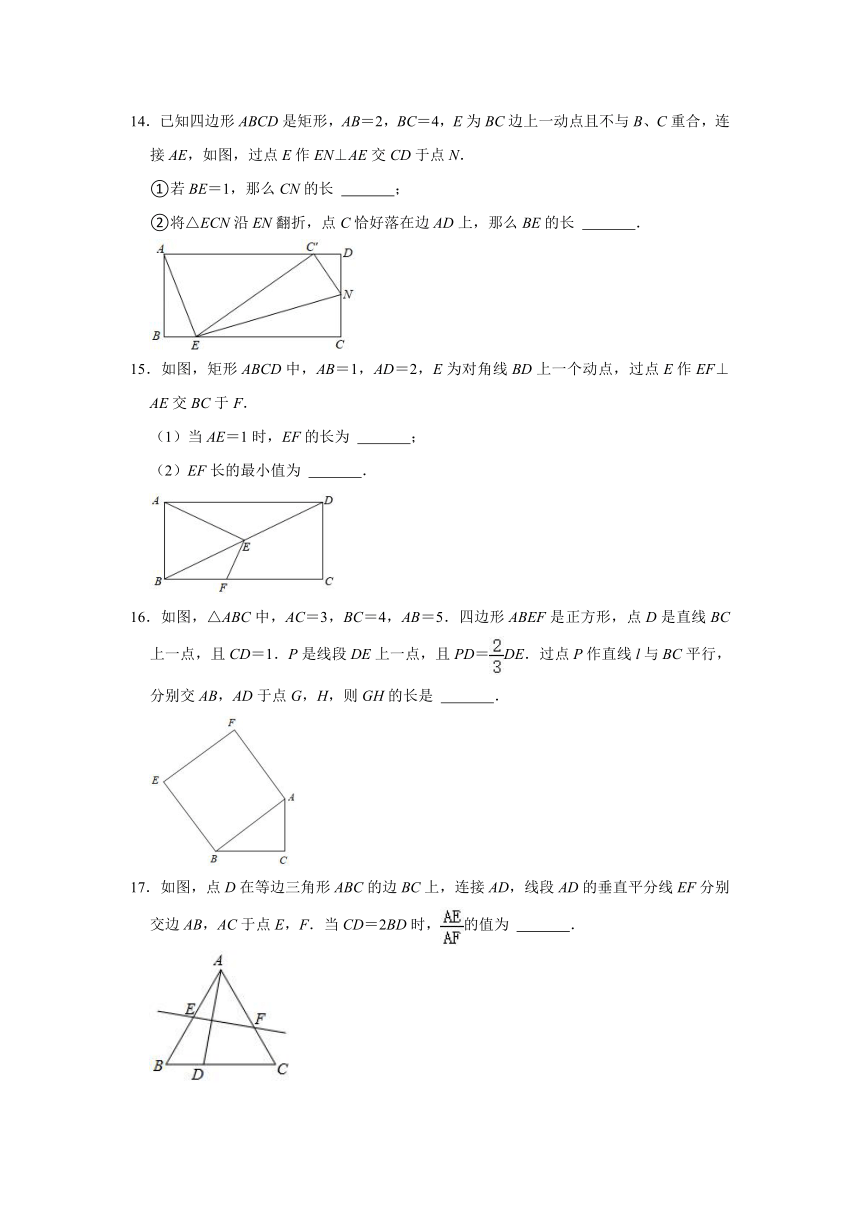
14.已知四边形ABCD是矩形,AB=2,BC=4,E为BC边上一动点且不与B、C重合,连接AE,如图,过点E作EN⊥AE交CD于点N.
①若BE=1,那么CN的长 ;
②将△ECN沿EN翻折,点C恰好落在边AD上,那么BE的长 .
15.如图,矩形ABCD中,AB=1,AD=2,E为对角线BD上一个动点,过点E作EF⊥AE交BC于F.
(1)当AE=1时,EF的长为 ;
(2)EF长的最小值为 .
16.如图,△ABC中,AC=3,BC=4,AB=5.四边形ABEF是正方形,点D是直线BC上一点,且CD=1.P是线段DE上一点,且PD=DE.过点P作直线l与BC平行,分别交AB,AD于点G,H,则GH的长是 .
17.如图,点D在等边三角形ABC的边BC上,连接AD,线段AD的垂直平分线EF分别交边AB,AC于点E,F.当CD=2BD时,的值为 .
18.如图,在正方形ABCD中,以AB为腰向正方形内部作等腰△ABE,点G在CD上,且CG=3DG.连接BG并延长,与AE交于点F,与AD延长线交于点H.连接DE交BH于点K,连接CK.若AE2=BF BH,FG=,则S四边形EFKC= .
19.如图,在菱形ABCD中,对角线AC=4,BD=2,AC,BD相交于点O,过点C作CE⊥AB交AB的延长线于点E,过点O作OF⊥CE交CE于点F,则OF的长度为 .
20.已知AC,EC分别是矩形ABCD和EFCG的对角线,点E在△ABC内,且=k,∠CAE+∠CBE=90°.
(1)求证:△CAE∽△CBF;
(2)若BE=2,AE=4,CE=6,求k的值.
参考答案
1.解:①∵在正方形ABCD中,∠NBC=∠ECD=90°,
∴BC=CD,∠BCN+∠GCD=90°,
∵CG⊥DE,
∴∠CDG+∠GCD=90°,
∴∠BCN=∠CDG,
∴△NBC≌△ECD(ASA),
∴DE=CN,
故①正确;
②∵在正方形ABCD中,AB∥CD,
∴△NBH∽△CDH,
∴=,
∵△NBC≌△ECD(ASA),E为BC的中点,四边形ABCD是正方形,
∴NB=BC=CD,
∴==,
故②正确;
③如下图所示,过H点作IJ∥AD,
∵△NBH∽△CDH,
∴I③J=HJ,
∴HI=IJ=DC,
∴S△DEC=EC DC,S△BNH=BN HI=EC×DC=×(×EC×DC),
∴S△DEC=3 S△BNH,
故③正确;
④过点B作BP⊥CN于点P,BQ⊥DG交DE的延长线上于点Q,
∴∠BPC=∠BQD=∠PGQ=90°,
∴四边形PBQG是矩形,
∴∠PBQ=90°,
∵∠ABC=90°,
∴∠NBP=∠QBE,
由①得△NBC≌△ECD,
∴EC=BN,
∵E是BC的中点,
∴BE=EC,
∴BE=BN,
∵∠BPN=∠BQE=90°,
∴△BPN≌△BQE(AAS),
∴BP=BQ,
∴四边形PBQG是正方形,
∴∠BGE=45°,
故④正确;
⑤如图所示,连接N,E,
设BN=x,则BE=EC=x,BC=2x,
∵CG⊥DE,∠NBC=90°,
∴CN===,
EN===,
由△ECN面积可得CN GE=EC BN,
∴GE=,
∴GN==,
∴GN+GE=+=,
∴GC=CN﹣GN=﹣=,
∵AB∥CD,
∴△NGB∽△CGF,
∴,
∴BG=FG,
∴BG=BF,FC=BN=x,
∴BG=×=,
∴GN+GE=BG,
故⑤正确;
综上所述,故选:D.
2.解:如图,作CM⊥DF于M.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∴∠DAB=∠B=∠ADC=90°,
∵∠ADF+∠CDF=90°,∠CDF+∠DCM=90°,
∴∠ADF=∠DCM,
∵DF⊥AE,CM⊥DF,
∴∠AFD=∠CMD=90°,
∴△DAF≌△CDM,
∴CM=DF,DM=AF,
∵∠ADF+∠DAE=90°,∠DAE+∠BAE=90°,
∴∠BAE=∠ADF,
∵BE=CE,
∴AB=2BE,
∴tan∠BAE=tan∠ADF==,
∴=,
∴DM=MF,∵CM⊥DF,
∴CD=CF,故①正确,
∴∠CDF=∠CFD,
∵∠CDG=∠CFG=90°,
∴∠GFD=∠GDF,
∴GF=GD,
∵∠GDF+∠DAF=90°,∠GFD+∠AFG=90°,
∴∠GAF=∠GFA,
∴GF=GA,
∴GD=GA,
∴G是AD中点,故②正确,
∵∠AFD=∠GFC,
∴∠AFG=∠CFD,∠GAF=∠CDF,
∴△DCF∽△AGF,故③正确,
设AF=a,则DF=2a,AB=a,BE=a,
∴AE=a,EF=a,
∴=,故④正确,
故选:D.
3.解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,故①正确;
在Rt△ABH中,∠AHB=90°﹣∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在Rt△ABH和Rt△DCF中,
,
∴Rt△ABH≌Rt△DCF(ASA),
∴AH=DF,∠CFD=∠AHB=67.5°,故②正确;
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故④正确;
∵∠FDE=45°,∠DFE=∠FAE+∠AEF=22.5°+45°=67.5°,
∴∠DEF=180°﹣45°﹣67.5°=67.5°,
∴DF=DE,故③正确;
如图,连接HE,
∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故⑤错误,
∴正确的是①②③④,
故选:C.
4.解:∵四边形ABCD是正方形,
∴AD=AB=CD=BC,∠CDE=∠DAF=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=∠ADF+∠CDF=90°,
∴∠ADF=∠DCE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(ASA),
∴DE=AF;故①正确;
∵AB∥CD,
∴=,
∵AF:FB=1:2,
∴AF:AB=AF:CD=1:3,
∴=,
∴=,
∵AC=AB,
∴=,
∴AN=AB;故②正确;
作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC=a,
∵∠DCE=∠DCM,∠CDE=∠CMD=90°,
∴△CMD∽△CDE,
∵∠DCE+∠DEC=∠DCE+∠HCG=90°,
∴∠DEC=∠HCG,
又∵∠CDE=∠CHG=90°,
∴△GHC∽△CDE,由△CMD∽△CDE,可得CM=a,
由△GHC∽△CDE,可得CH=a,
∴CH=MH=CM,
∵GH⊥CM,
∴GM=GC,
∴∠GMH=∠GCH,
∵∠FMG+∠GMH=90°,∠DCE+∠GCM=90°,
∴∠FMG=∠DCE,
∵∠ADF=∠DCE,
∴∠ADF=∠GMF;故③正确,
(补充方法:延长MF交CG的延长线于T,证明CG=GT,利用直角三角形斜边中线的性质即可解决问题)
设△ANF的面积为m,
∵AF∥CD,
∴==,△AFN∽△CDN,
∴△ADN的面积为3m,△DCN的面积为9m,
∴△ADC的面积=△ABC的面积=12m,
∴S△ANF:S四边形CNFB=1:11,故④错误,
故选:C.
5.解:(1)∵四边形ABCD为正方形,
∴AD=AB=∴BC,∠DAE=∠ABF=90°,
∵E、F分别为正方形ABCD的边AB,BC的中点,
∴AE=AB,BF=BC,
∴AE=BF,
∴△DAE≌△ABF(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAM=90°,
∴∠ADE+∠DAM=90°,
∴∠AME=∠ADE+∠DAM=90°,
故①正确;
(2)设AF与BD交于点N,正方形ABCD的边长为4,
则AE=BE=BF=2,
∴DE=AF==2,
∵AD∥BF,
∴△BFN∽△DAN,
∴==,
∴FN=,AN=,
∵S△AED=AD AE=DE AM,
∴AM===,
∴MN=AF﹣AM﹣NF=,
∴AM≠MN,
若∠BAF=∠EDB,
则∠ADE=∠EDB,
又∵DM=DM,∠DMA=∠DMN=90°,
∴△DAM≌△DNM(ASA),
∴AM=MN,
不符合题意,
故②错误;
(3)由(1)知,∠BAF=∠ADE,
又∵∠AME=∠EAD=∠AMD=90°,
∴△AME∽△DMA∽△DAE,
∴===,
∴AM=2EM,DM=2AM,
∴MD=2AM=4EM,
故③正确;
(4)由(2)知AM=,MN=,FN=,
∴MF=MN+FN=+=,
∴=,
故④正确;
故选:B.
6.解:①如图,过G作GK⊥AD于K,
∴∠GKF=90°,
∵四边形ABCD是正方形,
∴∠ADE=90°,AD=AB=GK,
∴∠ADE=∠GKF,
∵AE⊥FH,
∴∠AOF=∠OAF+∠AFO=90°,
∵∠OAF+∠AED=90°,
∴∠AFO=∠AED,
∴△ADE≌△GKF(AAS),
∴FG=AE,
∵FH是AE的中垂线,
∴AE=2AO,
∴FG=2AO,
故①正确;
②∵tan∠DAE=tan∠AHO===,
设OF=x,AO=2x,
∴AE=FG=OH=4x,
∴FH=5x,
∴HG=x,
∴AH=HE==2x,
∵△HBG∽△HOA,
∴=,
∴=,
∴BH=x,
∴==5,
∴EH=5BH,故②正确;
③延长DO交AB于P,则OD=OP,
∴AE=PD,
∴Rt△ADE≌Rt△PDA(HL),
∴AP=DE,
∴AP=PB,
∴△ADP≌△BCP(SAS),
∴PD=PC,
∵PC>BC,
∴PC>CD,
∵PO=DO,
∴OD不垂直于CM,故③错误;
④∵FH是AE的中垂线,
∴AH=EH,
∴∠HAE=∠HEA,
∵AB∥CD,
∴∠HAE=∠AED,
Rt△ADE中,∵O是AE的中点,
∴OD=AE=OE,
∴∠ODE=∠AED,
∴∠HEA=∠AED=∠ODE,
当∠DOE=∠HEA时,OD∥HE,
但AE>AD,即AE>CD,
∴OE>DE,即∠DOE≠∠HEA,
∴OD与HE不平行,
故④不正确;
⑤设正方形ABCD的边长为2x,则AD=AB=2x,DE=EC=x,
∴AE=x,AO=x,
易得△ADE∽△HOA,
∴=,
∴=,
∴HO=x,
Rt△AHO中,由勾股定理得:AH==,
∴BH=AH﹣AB=﹣2x=,
∴=,
延长CM、BA交于R,
∵RA∥CE,
∴∠ARO=∠ECO,
∵AO=EO,∠ROA=∠COE,
∴△ARO≌△ECO(,
∴AR=CE,
∵AR∥CD,
∴=,
∴==,
∴==,
故⑤正确;
⑥由①知:∠HAE=∠AEH=∠OED=∠ODE,
∴△HAE∽△ODE,
∴=,
∵AE=2DE,OD=DE,
∴DE 2DE=AH DE,
∴2DE2=AH DE,
故⑥正确;
⑦由⑤知:HC==x,
∵AE=2AO=OH=x,
tan∠EAD===,
∵AO=,
∴OF=x,
∵FG=AE=x,
∴OG=x﹣x=x,
∴OG+BH=x+x,
∴OG+BH≠HC,
故⑦不正确;
本题正确的有;①②⑤⑥,4个,
故选:B.
7.解:①连接AC,与BE交于点Q,如图1,
∵AB=BC,∠BAC=∠ACB=45°,
∴∠BAC=∠BCA,
∵∠BAH=∠BCH=60°,
∴∠CAH=∠ACH,
∴HA=HC,
∵DA=DC,DH=DH,
∴△ADH≌△CDH(SSS),
∴∠ADH=∠CDH=∠ADC=,
∴∠BAQ=∠CDH,
∵∠ABQ=∠DCH=90°﹣60°=30°,AB=DC,
∴△ABQ≌△DCH(AAS),
∴AQ=DH,
∵AB=BC=BE,∠ABE=30°,
∴∠AEB=∠EAB=75°,
∵∠AQE=∠ABQ+∠BAQ=30°+45°=75°,
∴AQ=AE,
∴AE=DH,
故①正确;
②设AF与BE交于点M,如图2,
∵∠BAF=60°,∠ABM=30°,
∴∠AMB=90°,
∴AM=AB,
∴,
∵,
∴4S△AEB=S正方形ABCD,
故②正确;
③过点H作HN⊥CD于点N,如图3,
设HN=a,
∵∠CDH=45°,
∴DN=HN=a,
∵∠HCN=30°,
∴CH=2HN=2a,CN=HN=a,
∵AH=CH,AF=AB=CD,
∴AH=2a,AF=(+1)a,
∴HF=AF﹣AH=(﹣1)a,
∴HF AD=(﹣1)a (+1)a=2a2,
∵,
∴DH2=2a2,
∴DH2=HF AD,
故③正确;
④由③知,EH=CE﹣CH=(+1)a﹣2a=()a,
∴3EH=(3﹣3)a,
∵AB=(+1)a,∠ABP=30°,
∴BP==,
∴EP=BP﹣BE=﹣(+1)a=a,
∴5EP=a,
∴5EP≠3EH,
故④错误;
故选:B.
8.解:①∵四边形ABCD为正方形,
∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,
∴BF=CG,
∵在△ABF和△BCG中,
,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;
②∵在△BNF和△BCG中,∠CBG=∠NBF,∠BCG=∠BNF=90°,
∴△BNF∽△BCG,∴==,
∴BN=NF;②错误;
③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,
AF==,
∵S△ABF=AF BN=AB BF,
∴BN=,NF=BN=,
∴AN=AF﹣NF=,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH=,NH=,BN∥EH,
∴AH=,=,解得:MN=,
∴BM=BN﹣MN=,MG=BG﹣BM=,
∴=;③正确;
④连接AG,FG,根据③中结论,
则NG=BG﹣BN=,
∵S四边形CGNF=S△CFG+S△GNF=CG CF+NF NG=1+=,
S四边形ANGD=S△ANG+S△ADG=AN GN+AD DG=+=,
∴S四边形CGNF≠S四边形ANGD,④错误;
故选:A.
9.解:∵四边形ABCD是正方形,
∴AB=AD,AD∥BC,
∵DE⊥AG,BF∥DE,
∴BF⊥AG,
∴∠AED=∠DEF=∠BFE=90°,
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
∴△AED≌△BFA(AAS);故①正确;
∴DE=AF,AE=BF,
∴DE﹣BF=AF﹣AE=EF,故②正确;
∵AD∥BC,
∴∠DAE=∠BGF,
∵DE⊥AG,BF⊥AG,
∴∠AED=∠GFB=90°,
∴△BGF∽△DAE,故③正确;
∵DE,BG,FG没有等量关系,
故不能判定DE﹣BG=FG正确.故④错误(也可以用排除法判断);
故选:C.
10.解:∵四边形ABCD是边长为6的正方形,点E是BC的中点,
∴AB=AD=BC=CD=6,BE=CE=3,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,
∴△ABE≌△DCE(SAS)
∴∠DEC=∠AEB,∠BAE=∠CDE,DE=AE,故①正确,
∵AB=BC,∠ABG=∠CBG,BG=BG,
∴△ABG≌△CBG(SAS)
∴∠BAE=∠BCF,
∴∠BCF=∠CDE,且∠CDE+∠CED=90°,
∴∠BCF+∠CED=90°,
∴∠CHE=90°,
∴CF⊥DE,故②正确,
∵∠CDE=∠BCF,DC=BC,∠DCE=∠CBF=90°,
∴△DCE≌△CBF(ASA),
∴CE=BF,
∵CE=BC=AB,
∴BF=AB,
∴AF=FB,故③正确,
③解法二:∵四边形ABCD是正方形,
∴BC∥AD,
∵E是BC的中点,
∴==,
∵AB∥CD,
∴==,
∵AB=CD,
∴BF=AB.
∵DC=6,CE=3,
∴DE===3,
∵S△DCE=×CD×CE=×DE×CH,
∴CH=,
∵∠CHE=∠CBF,∠BCF=∠ECH,
∴△ECH∽△FCB,
∴=,
∴CF==3,
∴HF=CF﹣CH=,
∴=,故④正确,
故选:D.
11.解:如图1,∵四边形ABCD是正方形,
∴∠EBM=∠ADM=∠FDN=∠ABD=45°,
∵∠MAN=∠EBM=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∴=,
∴=,
∵∠AMB=∠EMN,
∴△AMB∽△NME,故①正确,
∴∠AEN=∠ABD=45°
∴∠NAE=∠AEN=45°,
∴△AEN是等腰直角三角形,故②正确,
在△ABE和△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=CD,
∴CE=CF,
假设正方形边长为1,设CE=x,则BE=1﹣x,
如图2,连接AC,交EF于H,
∵AE=AF,CE=CF,
∴AC是EF的垂直平分线,
∴AC⊥EF,OE=OF,
Rt△CEF中,OC=EF=x,
△EAF中,∠EAO=∠FAO=22.5°=∠BAE=22.5°,
∴OE=BE,
∵AE=AE,
∴Rt△ABE≌Rt△AOE(HL),
∴AO=AB=1,
∴AC==AO+OC,
∴1+x=,
x=2﹣,
∴==,故③不正确,
③如图3,
∴将△ADF绕点A顺时针旋转90°得到△ABH,则AF=AH,∠DAF=∠BAH,
∵∠EAF=45°=∠DAF+∠BAE=∠HAE,
∵∠ABE=∠ABH=90°,
∴H、B、E三点共线,
在△AEF和△AEH中,
,
∴△AEF≌△AEH(SAS),
∴EF=EH=BE+BH=BE+DF,故④正确,
如图4中,设正方形的边长为2a,则DF=CF=a,AF=a,
∵DF∥AB,
∴==,
∴AN=NE=AF=a,
∴AE=AN=a
∴BE===a,
∴EC=a=BC,故⑤正确.
故选:C.
12.解:如图,过点A作AE⊥BC于点E,DH⊥BC于点H,作FB⊥AB于B,FC⊥BC于C,BF与CF交于点F,
取BF的中点G,连接AG,CG,
在RtDBH中,
∵∠DBC=45°,BD=2,
∴DH=BH=2,
∵AD∥BC,
∴AE=DH=2,
∵∠ABF=∠AEB=∠BCF=90°
∴∠ABE+∠FCB=∠ABE+∠BAE=90°,
∴∠BAE=∠FBC,
∴△BAE∽△FBC,
∴==,
设AB=4x,则BF=6x,
∴BG=FG=BF=3x,
∴AG==5x,
∴≥==.
故答案为:.
13.解:如图,取AD中点F,连接EF,过点D作DG⊥EF于G,DH⊥BE于H,
设BD=a,
∴AD=3BD=3a,AB=4a,
∵点E为CD中点,点F为AD中点,CD=6,
∴DF=a,EF∥AC,DE=3,
∴∠FED=∠ACD=45°,
∵∠BED=45°,
∴∠FED=∠BED,∠FEB=90°,
∵DG⊥EF,DH⊥BE,
∴四边形EHDG是矩形,DG=DH,
∴四边形DGEH是正方形,
∴DE=DG=3,DH∥EF,
∴DG=DH=3,
∵DH∥EF,
∴∠BDH=∠DFG,
∴△BDH∽△DFG,
∴,
∴=,
∴BH=2,
∴BD===,
∴AB=4,
故答案为:4.
14.解:①∵BE=1,
∴CE=BC﹣BE=4﹣1=3,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EN⊥AE,
∴∠AEN=90°,
∴∠BEA+∠NEC=90°,
∴∠BAE=∠NEC,
∴△ABE∽△ECN,
∴=,
∴=,
解得:CN=;
故答案为:;
②过点E作EF⊥AD于F,如图所示:
则四边形ABEF是矩形,
∴AB=EF=2,AF=BE,
由折叠的性质得:CE=C′E,CN=C′N,∠EC′N=∠C=90°,
∴∠NC′D+∠EC′F=90°,
∵∠C′ND+∠NC′D=90°,
∴∠EC′F=∠C′ND,
∵∠D=∠EFC′,
∴△EC′F∽△NC′D,
∴==,
∴==,
∵=,
∴=,
∴==,
∴C′D=BE,
设BE=x,则C′D=AF=x,C′F=4﹣2x,CE=4﹣x,
∴=,=,
∴DN=x(2﹣x),CN=,
∴CN+DN=x(2﹣x)+=CD=2,
解得:x=2或x=,
∴BE=2或BE=.
故答案为:2或.
15.解:(1)如图,连接AF交BD于点G,
∵四边形ABCD是矩形,
∴∠ABF=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠ABF=∠AEF=90°,
在Rt△ABF和Rt△AEF中,
,
∴Rt△ABF≌Rt△AEF(HL),
∴BF=EF,
∵AB=AE,
∴AF是BE的垂直平分线,
∴∠AGB=90°,
∴∠BAF=∠FBG,
∵AD∥BC,
∴∠ADB=∠FBG,
∴∠ADB=∠BAF,
∴△ABF∽△DAB,
∴=,
∴=,
∴BF=,
∴当AE=1时,EF的长为;
故答案为:;
(2)如图,因为EF⊥AE,
所以当点F与点B重合时,EF长最小,
在矩形ABCD中,
∵AB=1,AD=2,
∴BD==,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BAD=∠AEF=90°,
∵∠DBA=∠AFE,
∴△DBA∽△AFE,
∴=,
∴=,
∴EF=.
故答案为:.
16.解:∵△ABC中,AC=3,BC=4,AB=5,
∴AC2+BC2=25,AB2=25,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,
①当点D位于C点左侧时,如图:
设直线l交BE于点M,
∵l∥BC,
∴,∠MGB=∠ABC,
又∵四边形ABEF是正方形,且PD1=D1E,
∴BE=AB=5,∠EBA=90°,
即,
解得:BM=,
∵∠MGB=∠ABC,∠EBA=∠ACB=90°,
∴△GBM∽△BCA,
∴,
∴,
解得:GB=,
∴AG=AB﹣GB=,
∵l∥BC,
∴△AGH∽△ABD1,
∴,
∵CD1=1,
∴BD1=BC﹣CD1=3,
∴,
解得:GH=;
②当点D位于C点右侧时,如图:
与①同理,此时CD2=BC+CD1=5,
∴,
解得:GH=,
综上,GH的长为或,
故答案为:或.
17.解:如图,连接DE,DF,
∵EF垂直平分AD,
∴AE=DE,AF=DF,
在△AEF和△DEF中,
,
∴△AEF≌△DEF(SSS),
∴∠EAF=∠EDF=60°,
∴∠EDB+∠FDC=120°,
∵∠EDB+∠BED=120°,
∴∠BED=∠FDC,
∵∠B=∠C=60°,
∴△EBD∽△DCF,
∴==,
设BD=x,则CD=2x,BE=y,
∴CF=,
∴DE=AE=AB﹣BE=3x﹣y,
∴DF=AF=AC﹣CF=BC﹣CF=3x﹣,
∴=,
∴8x2=5xy,
∴=,
∴=====.
故答案为:.
18.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠ADC=90°,
∵CG=3DG,
∴可以假设DG=3a,CG=9a,
则AB=AD=BC=CD=12a,
∴DG∥AB,
∴===,
∴DH=4a,GH=5a,BH=20a,
∵AE2=BF BH,AE=AB,
∴AB2=BF BH,
∴=,∵∠ABF=∠ABH,
∴△ABF∽HBA,
∴∠AFB=∠BAH=90°,
∴AF==a,BF=a,
∴FG=BH﹣BF﹣GH=a,
∵AE=AD,
∴∠ADE=∠AED,
∵∠ADE+∠GDK=90°,∠KEF+∠EKF=90°,∠EKF=∠GKD,
∴∠GDK=∠GKD,
∴GD=GK=3a,
作KM⊥CD于M,EN⊥AB于N,
∵=,
∴KM=a,
∵△AFB≌△ANE,
∴EN=BF=a,
∴S四边形EFKC=S△EFK+S△ECK
=s△EFK+(S△CDE﹣S△CDK)
=×a×a+(×12a×a﹣×12a×a)
=a2,
∵FG=a=,
∴a=,
∴S四边形EFKC=,
故答案为.
19.解:∵四边形ABCD是菱形,
∴AO=2,BO=1,AC⊥BD,
∴AB===,
∵S菱形ABCD=×AC×BD=AB×CE,
∴4=×CE,
∴CE=,
∵∠OFC=∠AEC=90°,∠ACE=∠OCF,
∴△OCF∽△ACE,
∴,
∴CE=2CF,
∴CF=EF=,
∴OF===,
故答案为:.
20.(1)证明:∵四边形ABCD和EFCG均为正方形,
∴∠ABC=∠EFC=90°,
∵=k,
∴△ABC∽△EFC,
∴=,∠ACB=∠ECF,
∴=,∠ACE=∠BCF,
∴△CAE∽△CBF;
(2)解:∵△CAE∽△CBF,
∴=,
∵=k,
∴AB=kBC,
∴AC===BC,
∴=,
∴==,
∵AE=4,
∴BF=,
∵∠CAE+∠CBE=90°.∠CAE=∠CBF,
∴∠CBF+∠CBE=90°.
∴∠EBF=90°,
∴EF2=EB2+BF2=22+=4+,
∵=k,
∴FC=EF,
∴CE===EF,
∴CE2=(1+)(4+)=36,
解得k=±(负值舍去),
∴k=.
自主提升训练(附答案)
1.如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,延长BG交CD于点F,延长CG交BD于点H,交AB于N下列结论:
①DE=CN;②=;③S△DEC=3S△BNH;④∠BGN=45°;⑤GN+EG=BG;
其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
2.如图,正方形ABCD中,E为BC中点,连接AE,DF⊥AE于点F,连接CF,FG⊥CF交AD于点G,下列结论:①CF=CD;②G为AD中点;③△DCF∽△AGF;④=,其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:①BH垂直平分AE;②AH=DF;③DF=DE;④∠AEF=45°;⑤S四边形EFHG=S△DEF+S△AGH,其中正确的结论有( )个.
A.2 B.3 C.4 D.5
4.如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=BC,连接GM.有如下结论:①DE=AF;②AN=AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.②③④
5.如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M则下列结论①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM;④AM=MF,其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
6.如图,正方形ABCD中,E为CD的中点,AE的垂直平分线分别交AD,BC及AB的延长线于点F,G,H,连接HE,HC,ED,连接CO并延长交AD于点M,则下列结论中:①FG=2AO;②HE=5BH;③OD⊥CM;④OD∥HE;⑤;⑥2DE2=AH DE;⑦GO+BH=HC.正确的结论的个数为( )
A.3 B.4 C.5 D.6
7.如图,在正方形ABCD中,△ABF和△BCE是等边三角形,边AF与CE交于点H,BE的延长线交AD于点P,AF的延长线交CD于点G,连接DH.给出下列结论:
①AE=DH;
②4S△AEB=S正方形ABCD;
③DH2=HF AD;
④5EP=3EH.
其中正确的是( )
A.①③ B.①②③ C.①③④ D.①②③④
8.如图所示,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N,下列结论:①AF⊥BG;②BN=NF;③=;④S四边形CGNF=S四边形ANGD.其中正确的结论的序号是( )
A.①③ B.②④ C.①② D.③④
9.如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.给出以下结论:①△AED≌△BFA;②DE﹣BF=EF;③△BGF∽△DAE;④DE﹣BG=FG.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①∠DEC=∠AEB;②CF⊥DE;③AF=BF;④=,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
11.如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连接EN、EF,有以下结论:①△ABM∽△NEM;②△AEN是等腰直角三角形;③当AE=AF时,;④BE+DF=EF;⑤若点F是DC的中点,则CE=CB,其中正确的个数是( )
A.2 B.3 C.4 D.5
12.如图,在四边形ABCD中,AD∥BC,∠DBC=45°,BD=2,BC=3,则的最小值为 .
13.如图,在△ABC中,点D是AB边上的一点,且AD=3BD,连接CD并取CD的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6,则AB的长为 .
14.已知四边形ABCD是矩形,AB=2,BC=4,E为BC边上一动点且不与B、C重合,连接AE,如图,过点E作EN⊥AE交CD于点N.
①若BE=1,那么CN的长 ;
②将△ECN沿EN翻折,点C恰好落在边AD上,那么BE的长 .
15.如图,矩形ABCD中,AB=1,AD=2,E为对角线BD上一个动点,过点E作EF⊥AE交BC于F.
(1)当AE=1时,EF的长为 ;
(2)EF长的最小值为 .
16.如图,△ABC中,AC=3,BC=4,AB=5.四边形ABEF是正方形,点D是直线BC上一点,且CD=1.P是线段DE上一点,且PD=DE.过点P作直线l与BC平行,分别交AB,AD于点G,H,则GH的长是 .
17.如图,点D在等边三角形ABC的边BC上,连接AD,线段AD的垂直平分线EF分别交边AB,AC于点E,F.当CD=2BD时,的值为 .
18.如图,在正方形ABCD中,以AB为腰向正方形内部作等腰△ABE,点G在CD上,且CG=3DG.连接BG并延长,与AE交于点F,与AD延长线交于点H.连接DE交BH于点K,连接CK.若AE2=BF BH,FG=,则S四边形EFKC= .
19.如图,在菱形ABCD中,对角线AC=4,BD=2,AC,BD相交于点O,过点C作CE⊥AB交AB的延长线于点E,过点O作OF⊥CE交CE于点F,则OF的长度为 .
20.已知AC,EC分别是矩形ABCD和EFCG的对角线,点E在△ABC内,且=k,∠CAE+∠CBE=90°.
(1)求证:△CAE∽△CBF;
(2)若BE=2,AE=4,CE=6,求k的值.
参考答案
1.解:①∵在正方形ABCD中,∠NBC=∠ECD=90°,
∴BC=CD,∠BCN+∠GCD=90°,
∵CG⊥DE,
∴∠CDG+∠GCD=90°,
∴∠BCN=∠CDG,
∴△NBC≌△ECD(ASA),
∴DE=CN,
故①正确;
②∵在正方形ABCD中,AB∥CD,
∴△NBH∽△CDH,
∴=,
∵△NBC≌△ECD(ASA),E为BC的中点,四边形ABCD是正方形,
∴NB=BC=CD,
∴==,
故②正确;
③如下图所示,过H点作IJ∥AD,
∵△NBH∽△CDH,
∴I③J=HJ,
∴HI=IJ=DC,
∴S△DEC=EC DC,S△BNH=BN HI=EC×DC=×(×EC×DC),
∴S△DEC=3 S△BNH,
故③正确;
④过点B作BP⊥CN于点P,BQ⊥DG交DE的延长线上于点Q,
∴∠BPC=∠BQD=∠PGQ=90°,
∴四边形PBQG是矩形,
∴∠PBQ=90°,
∵∠ABC=90°,
∴∠NBP=∠QBE,
由①得△NBC≌△ECD,
∴EC=BN,
∵E是BC的中点,
∴BE=EC,
∴BE=BN,
∵∠BPN=∠BQE=90°,
∴△BPN≌△BQE(AAS),
∴BP=BQ,
∴四边形PBQG是正方形,
∴∠BGE=45°,
故④正确;
⑤如图所示,连接N,E,
设BN=x,则BE=EC=x,BC=2x,
∵CG⊥DE,∠NBC=90°,
∴CN===,
EN===,
由△ECN面积可得CN GE=EC BN,
∴GE=,
∴GN==,
∴GN+GE=+=,
∴GC=CN﹣GN=﹣=,
∵AB∥CD,
∴△NGB∽△CGF,
∴,
∴BG=FG,
∴BG=BF,FC=BN=x,
∴BG=×=,
∴GN+GE=BG,
故⑤正确;
综上所述,故选:D.
2.解:如图,作CM⊥DF于M.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∴∠DAB=∠B=∠ADC=90°,
∵∠ADF+∠CDF=90°,∠CDF+∠DCM=90°,
∴∠ADF=∠DCM,
∵DF⊥AE,CM⊥DF,
∴∠AFD=∠CMD=90°,
∴△DAF≌△CDM,
∴CM=DF,DM=AF,
∵∠ADF+∠DAE=90°,∠DAE+∠BAE=90°,
∴∠BAE=∠ADF,
∵BE=CE,
∴AB=2BE,
∴tan∠BAE=tan∠ADF==,
∴=,
∴DM=MF,∵CM⊥DF,
∴CD=CF,故①正确,
∴∠CDF=∠CFD,
∵∠CDG=∠CFG=90°,
∴∠GFD=∠GDF,
∴GF=GD,
∵∠GDF+∠DAF=90°,∠GFD+∠AFG=90°,
∴∠GAF=∠GFA,
∴GF=GA,
∴GD=GA,
∴G是AD中点,故②正确,
∵∠AFD=∠GFC,
∴∠AFG=∠CFD,∠GAF=∠CDF,
∴△DCF∽△AGF,故③正确,
设AF=a,则DF=2a,AB=a,BE=a,
∴AE=a,EF=a,
∴=,故④正确,
故选:D.
3.解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,故①正确;
在Rt△ABH中,∠AHB=90°﹣∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在Rt△ABH和Rt△DCF中,
,
∴Rt△ABH≌Rt△DCF(ASA),
∴AH=DF,∠CFD=∠AHB=67.5°,故②正确;
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故④正确;
∵∠FDE=45°,∠DFE=∠FAE+∠AEF=22.5°+45°=67.5°,
∴∠DEF=180°﹣45°﹣67.5°=67.5°,
∴DF=DE,故③正确;
如图,连接HE,
∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故⑤错误,
∴正确的是①②③④,
故选:C.
4.解:∵四边形ABCD是正方形,
∴AD=AB=CD=BC,∠CDE=∠DAF=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=∠ADF+∠CDF=90°,
∴∠ADF=∠DCE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(ASA),
∴DE=AF;故①正确;
∵AB∥CD,
∴=,
∵AF:FB=1:2,
∴AF:AB=AF:CD=1:3,
∴=,
∴=,
∵AC=AB,
∴=,
∴AN=AB;故②正确;
作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC=a,
∵∠DCE=∠DCM,∠CDE=∠CMD=90°,
∴△CMD∽△CDE,
∵∠DCE+∠DEC=∠DCE+∠HCG=90°,
∴∠DEC=∠HCG,
又∵∠CDE=∠CHG=90°,
∴△GHC∽△CDE,由△CMD∽△CDE,可得CM=a,
由△GHC∽△CDE,可得CH=a,
∴CH=MH=CM,
∵GH⊥CM,
∴GM=GC,
∴∠GMH=∠GCH,
∵∠FMG+∠GMH=90°,∠DCE+∠GCM=90°,
∴∠FMG=∠DCE,
∵∠ADF=∠DCE,
∴∠ADF=∠GMF;故③正确,
(补充方法:延长MF交CG的延长线于T,证明CG=GT,利用直角三角形斜边中线的性质即可解决问题)
设△ANF的面积为m,
∵AF∥CD,
∴==,△AFN∽△CDN,
∴△ADN的面积为3m,△DCN的面积为9m,
∴△ADC的面积=△ABC的面积=12m,
∴S△ANF:S四边形CNFB=1:11,故④错误,
故选:C.
5.解:(1)∵四边形ABCD为正方形,
∴AD=AB=∴BC,∠DAE=∠ABF=90°,
∵E、F分别为正方形ABCD的边AB,BC的中点,
∴AE=AB,BF=BC,
∴AE=BF,
∴△DAE≌△ABF(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAM=90°,
∴∠ADE+∠DAM=90°,
∴∠AME=∠ADE+∠DAM=90°,
故①正确;
(2)设AF与BD交于点N,正方形ABCD的边长为4,
则AE=BE=BF=2,
∴DE=AF==2,
∵AD∥BF,
∴△BFN∽△DAN,
∴==,
∴FN=,AN=,
∵S△AED=AD AE=DE AM,
∴AM===,
∴MN=AF﹣AM﹣NF=,
∴AM≠MN,
若∠BAF=∠EDB,
则∠ADE=∠EDB,
又∵DM=DM,∠DMA=∠DMN=90°,
∴△DAM≌△DNM(ASA),
∴AM=MN,
不符合题意,
故②错误;
(3)由(1)知,∠BAF=∠ADE,
又∵∠AME=∠EAD=∠AMD=90°,
∴△AME∽△DMA∽△DAE,
∴===,
∴AM=2EM,DM=2AM,
∴MD=2AM=4EM,
故③正确;
(4)由(2)知AM=,MN=,FN=,
∴MF=MN+FN=+=,
∴=,
故④正确;
故选:B.
6.解:①如图,过G作GK⊥AD于K,
∴∠GKF=90°,
∵四边形ABCD是正方形,
∴∠ADE=90°,AD=AB=GK,
∴∠ADE=∠GKF,
∵AE⊥FH,
∴∠AOF=∠OAF+∠AFO=90°,
∵∠OAF+∠AED=90°,
∴∠AFO=∠AED,
∴△ADE≌△GKF(AAS),
∴FG=AE,
∵FH是AE的中垂线,
∴AE=2AO,
∴FG=2AO,
故①正确;
②∵tan∠DAE=tan∠AHO===,
设OF=x,AO=2x,
∴AE=FG=OH=4x,
∴FH=5x,
∴HG=x,
∴AH=HE==2x,
∵△HBG∽△HOA,
∴=,
∴=,
∴BH=x,
∴==5,
∴EH=5BH,故②正确;
③延长DO交AB于P,则OD=OP,
∴AE=PD,
∴Rt△ADE≌Rt△PDA(HL),
∴AP=DE,
∴AP=PB,
∴△ADP≌△BCP(SAS),
∴PD=PC,
∵PC>BC,
∴PC>CD,
∵PO=DO,
∴OD不垂直于CM,故③错误;
④∵FH是AE的中垂线,
∴AH=EH,
∴∠HAE=∠HEA,
∵AB∥CD,
∴∠HAE=∠AED,
Rt△ADE中,∵O是AE的中点,
∴OD=AE=OE,
∴∠ODE=∠AED,
∴∠HEA=∠AED=∠ODE,
当∠DOE=∠HEA时,OD∥HE,
但AE>AD,即AE>CD,
∴OE>DE,即∠DOE≠∠HEA,
∴OD与HE不平行,
故④不正确;
⑤设正方形ABCD的边长为2x,则AD=AB=2x,DE=EC=x,
∴AE=x,AO=x,
易得△ADE∽△HOA,
∴=,
∴=,
∴HO=x,
Rt△AHO中,由勾股定理得:AH==,
∴BH=AH﹣AB=﹣2x=,
∴=,
延长CM、BA交于R,
∵RA∥CE,
∴∠ARO=∠ECO,
∵AO=EO,∠ROA=∠COE,
∴△ARO≌△ECO(,
∴AR=CE,
∵AR∥CD,
∴=,
∴==,
∴==,
故⑤正确;
⑥由①知:∠HAE=∠AEH=∠OED=∠ODE,
∴△HAE∽△ODE,
∴=,
∵AE=2DE,OD=DE,
∴DE 2DE=AH DE,
∴2DE2=AH DE,
故⑥正确;
⑦由⑤知:HC==x,
∵AE=2AO=OH=x,
tan∠EAD===,
∵AO=,
∴OF=x,
∵FG=AE=x,
∴OG=x﹣x=x,
∴OG+BH=x+x,
∴OG+BH≠HC,
故⑦不正确;
本题正确的有;①②⑤⑥,4个,
故选:B.
7.解:①连接AC,与BE交于点Q,如图1,
∵AB=BC,∠BAC=∠ACB=45°,
∴∠BAC=∠BCA,
∵∠BAH=∠BCH=60°,
∴∠CAH=∠ACH,
∴HA=HC,
∵DA=DC,DH=DH,
∴△ADH≌△CDH(SSS),
∴∠ADH=∠CDH=∠ADC=,
∴∠BAQ=∠CDH,
∵∠ABQ=∠DCH=90°﹣60°=30°,AB=DC,
∴△ABQ≌△DCH(AAS),
∴AQ=DH,
∵AB=BC=BE,∠ABE=30°,
∴∠AEB=∠EAB=75°,
∵∠AQE=∠ABQ+∠BAQ=30°+45°=75°,
∴AQ=AE,
∴AE=DH,
故①正确;
②设AF与BE交于点M,如图2,
∵∠BAF=60°,∠ABM=30°,
∴∠AMB=90°,
∴AM=AB,
∴,
∵,
∴4S△AEB=S正方形ABCD,
故②正确;
③过点H作HN⊥CD于点N,如图3,
设HN=a,
∵∠CDH=45°,
∴DN=HN=a,
∵∠HCN=30°,
∴CH=2HN=2a,CN=HN=a,
∵AH=CH,AF=AB=CD,
∴AH=2a,AF=(+1)a,
∴HF=AF﹣AH=(﹣1)a,
∴HF AD=(﹣1)a (+1)a=2a2,
∵,
∴DH2=2a2,
∴DH2=HF AD,
故③正确;
④由③知,EH=CE﹣CH=(+1)a﹣2a=()a,
∴3EH=(3﹣3)a,
∵AB=(+1)a,∠ABP=30°,
∴BP==,
∴EP=BP﹣BE=﹣(+1)a=a,
∴5EP=a,
∴5EP≠3EH,
故④错误;
故选:B.
8.解:①∵四边形ABCD为正方形,
∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,
∴BF=CG,
∵在△ABF和△BCG中,
,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;
②∵在△BNF和△BCG中,∠CBG=∠NBF,∠BCG=∠BNF=90°,
∴△BNF∽△BCG,∴==,
∴BN=NF;②错误;
③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,
AF==,
∵S△ABF=AF BN=AB BF,
∴BN=,NF=BN=,
∴AN=AF﹣NF=,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH=,NH=,BN∥EH,
∴AH=,=,解得:MN=,
∴BM=BN﹣MN=,MG=BG﹣BM=,
∴=;③正确;
④连接AG,FG,根据③中结论,
则NG=BG﹣BN=,
∵S四边形CGNF=S△CFG+S△GNF=CG CF+NF NG=1+=,
S四边形ANGD=S△ANG+S△ADG=AN GN+AD DG=+=,
∴S四边形CGNF≠S四边形ANGD,④错误;
故选:A.
9.解:∵四边形ABCD是正方形,
∴AB=AD,AD∥BC,
∵DE⊥AG,BF∥DE,
∴BF⊥AG,
∴∠AED=∠DEF=∠BFE=90°,
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
∴△AED≌△BFA(AAS);故①正确;
∴DE=AF,AE=BF,
∴DE﹣BF=AF﹣AE=EF,故②正确;
∵AD∥BC,
∴∠DAE=∠BGF,
∵DE⊥AG,BF⊥AG,
∴∠AED=∠GFB=90°,
∴△BGF∽△DAE,故③正确;
∵DE,BG,FG没有等量关系,
故不能判定DE﹣BG=FG正确.故④错误(也可以用排除法判断);
故选:C.
10.解:∵四边形ABCD是边长为6的正方形,点E是BC的中点,
∴AB=AD=BC=CD=6,BE=CE=3,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,
∴△ABE≌△DCE(SAS)
∴∠DEC=∠AEB,∠BAE=∠CDE,DE=AE,故①正确,
∵AB=BC,∠ABG=∠CBG,BG=BG,
∴△ABG≌△CBG(SAS)
∴∠BAE=∠BCF,
∴∠BCF=∠CDE,且∠CDE+∠CED=90°,
∴∠BCF+∠CED=90°,
∴∠CHE=90°,
∴CF⊥DE,故②正确,
∵∠CDE=∠BCF,DC=BC,∠DCE=∠CBF=90°,
∴△DCE≌△CBF(ASA),
∴CE=BF,
∵CE=BC=AB,
∴BF=AB,
∴AF=FB,故③正确,
③解法二:∵四边形ABCD是正方形,
∴BC∥AD,
∵E是BC的中点,
∴==,
∵AB∥CD,
∴==,
∵AB=CD,
∴BF=AB.
∵DC=6,CE=3,
∴DE===3,
∵S△DCE=×CD×CE=×DE×CH,
∴CH=,
∵∠CHE=∠CBF,∠BCF=∠ECH,
∴△ECH∽△FCB,
∴=,
∴CF==3,
∴HF=CF﹣CH=,
∴=,故④正确,
故选:D.
11.解:如图1,∵四边形ABCD是正方形,
∴∠EBM=∠ADM=∠FDN=∠ABD=45°,
∵∠MAN=∠EBM=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∴=,
∴=,
∵∠AMB=∠EMN,
∴△AMB∽△NME,故①正确,
∴∠AEN=∠ABD=45°
∴∠NAE=∠AEN=45°,
∴△AEN是等腰直角三角形,故②正确,
在△ABE和△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=CD,
∴CE=CF,
假设正方形边长为1,设CE=x,则BE=1﹣x,
如图2,连接AC,交EF于H,
∵AE=AF,CE=CF,
∴AC是EF的垂直平分线,
∴AC⊥EF,OE=OF,
Rt△CEF中,OC=EF=x,
△EAF中,∠EAO=∠FAO=22.5°=∠BAE=22.5°,
∴OE=BE,
∵AE=AE,
∴Rt△ABE≌Rt△AOE(HL),
∴AO=AB=1,
∴AC==AO+OC,
∴1+x=,
x=2﹣,
∴==,故③不正确,
③如图3,
∴将△ADF绕点A顺时针旋转90°得到△ABH,则AF=AH,∠DAF=∠BAH,
∵∠EAF=45°=∠DAF+∠BAE=∠HAE,
∵∠ABE=∠ABH=90°,
∴H、B、E三点共线,
在△AEF和△AEH中,
,
∴△AEF≌△AEH(SAS),
∴EF=EH=BE+BH=BE+DF,故④正确,
如图4中,设正方形的边长为2a,则DF=CF=a,AF=a,
∵DF∥AB,
∴==,
∴AN=NE=AF=a,
∴AE=AN=a
∴BE===a,
∴EC=a=BC,故⑤正确.
故选:C.
12.解:如图,过点A作AE⊥BC于点E,DH⊥BC于点H,作FB⊥AB于B,FC⊥BC于C,BF与CF交于点F,
取BF的中点G,连接AG,CG,
在RtDBH中,
∵∠DBC=45°,BD=2,
∴DH=BH=2,
∵AD∥BC,
∴AE=DH=2,
∵∠ABF=∠AEB=∠BCF=90°
∴∠ABE+∠FCB=∠ABE+∠BAE=90°,
∴∠BAE=∠FBC,
∴△BAE∽△FBC,
∴==,
设AB=4x,则BF=6x,
∴BG=FG=BF=3x,
∴AG==5x,
∴≥==.
故答案为:.
13.解:如图,取AD中点F,连接EF,过点D作DG⊥EF于G,DH⊥BE于H,
设BD=a,
∴AD=3BD=3a,AB=4a,
∵点E为CD中点,点F为AD中点,CD=6,
∴DF=a,EF∥AC,DE=3,
∴∠FED=∠ACD=45°,
∵∠BED=45°,
∴∠FED=∠BED,∠FEB=90°,
∵DG⊥EF,DH⊥BE,
∴四边形EHDG是矩形,DG=DH,
∴四边形DGEH是正方形,
∴DE=DG=3,DH∥EF,
∴DG=DH=3,
∵DH∥EF,
∴∠BDH=∠DFG,
∴△BDH∽△DFG,
∴,
∴=,
∴BH=2,
∴BD===,
∴AB=4,
故答案为:4.
14.解:①∵BE=1,
∴CE=BC﹣BE=4﹣1=3,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EN⊥AE,
∴∠AEN=90°,
∴∠BEA+∠NEC=90°,
∴∠BAE=∠NEC,
∴△ABE∽△ECN,
∴=,
∴=,
解得:CN=;
故答案为:;
②过点E作EF⊥AD于F,如图所示:
则四边形ABEF是矩形,
∴AB=EF=2,AF=BE,
由折叠的性质得:CE=C′E,CN=C′N,∠EC′N=∠C=90°,
∴∠NC′D+∠EC′F=90°,
∵∠C′ND+∠NC′D=90°,
∴∠EC′F=∠C′ND,
∵∠D=∠EFC′,
∴△EC′F∽△NC′D,
∴==,
∴==,
∵=,
∴=,
∴==,
∴C′D=BE,
设BE=x,则C′D=AF=x,C′F=4﹣2x,CE=4﹣x,
∴=,=,
∴DN=x(2﹣x),CN=,
∴CN+DN=x(2﹣x)+=CD=2,
解得:x=2或x=,
∴BE=2或BE=.
故答案为:2或.
15.解:(1)如图,连接AF交BD于点G,
∵四边形ABCD是矩形,
∴∠ABF=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠ABF=∠AEF=90°,
在Rt△ABF和Rt△AEF中,
,
∴Rt△ABF≌Rt△AEF(HL),
∴BF=EF,
∵AB=AE,
∴AF是BE的垂直平分线,
∴∠AGB=90°,
∴∠BAF=∠FBG,
∵AD∥BC,
∴∠ADB=∠FBG,
∴∠ADB=∠BAF,
∴△ABF∽△DAB,
∴=,
∴=,
∴BF=,
∴当AE=1时,EF的长为;
故答案为:;
(2)如图,因为EF⊥AE,
所以当点F与点B重合时,EF长最小,
在矩形ABCD中,
∵AB=1,AD=2,
∴BD==,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BAD=∠AEF=90°,
∵∠DBA=∠AFE,
∴△DBA∽△AFE,
∴=,
∴=,
∴EF=.
故答案为:.
16.解:∵△ABC中,AC=3,BC=4,AB=5,
∴AC2+BC2=25,AB2=25,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,
①当点D位于C点左侧时,如图:
设直线l交BE于点M,
∵l∥BC,
∴,∠MGB=∠ABC,
又∵四边形ABEF是正方形,且PD1=D1E,
∴BE=AB=5,∠EBA=90°,
即,
解得:BM=,
∵∠MGB=∠ABC,∠EBA=∠ACB=90°,
∴△GBM∽△BCA,
∴,
∴,
解得:GB=,
∴AG=AB﹣GB=,
∵l∥BC,
∴△AGH∽△ABD1,
∴,
∵CD1=1,
∴BD1=BC﹣CD1=3,
∴,
解得:GH=;
②当点D位于C点右侧时,如图:
与①同理,此时CD2=BC+CD1=5,
∴,
解得:GH=,
综上,GH的长为或,
故答案为:或.
17.解:如图,连接DE,DF,
∵EF垂直平分AD,
∴AE=DE,AF=DF,
在△AEF和△DEF中,
,
∴△AEF≌△DEF(SSS),
∴∠EAF=∠EDF=60°,
∴∠EDB+∠FDC=120°,
∵∠EDB+∠BED=120°,
∴∠BED=∠FDC,
∵∠B=∠C=60°,
∴△EBD∽△DCF,
∴==,
设BD=x,则CD=2x,BE=y,
∴CF=,
∴DE=AE=AB﹣BE=3x﹣y,
∴DF=AF=AC﹣CF=BC﹣CF=3x﹣,
∴=,
∴8x2=5xy,
∴=,
∴=====.
故答案为:.
18.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠BAD=∠ADC=90°,
∵CG=3DG,
∴可以假设DG=3a,CG=9a,
则AB=AD=BC=CD=12a,
∴DG∥AB,
∴===,
∴DH=4a,GH=5a,BH=20a,
∵AE2=BF BH,AE=AB,
∴AB2=BF BH,
∴=,∵∠ABF=∠ABH,
∴△ABF∽HBA,
∴∠AFB=∠BAH=90°,
∴AF==a,BF=a,
∴FG=BH﹣BF﹣GH=a,
∵AE=AD,
∴∠ADE=∠AED,
∵∠ADE+∠GDK=90°,∠KEF+∠EKF=90°,∠EKF=∠GKD,
∴∠GDK=∠GKD,
∴GD=GK=3a,
作KM⊥CD于M,EN⊥AB于N,
∵=,
∴KM=a,
∵△AFB≌△ANE,
∴EN=BF=a,
∴S四边形EFKC=S△EFK+S△ECK
=s△EFK+(S△CDE﹣S△CDK)
=×a×a+(×12a×a﹣×12a×a)
=a2,
∵FG=a=,
∴a=,
∴S四边形EFKC=,
故答案为.
19.解:∵四边形ABCD是菱形,
∴AO=2,BO=1,AC⊥BD,
∴AB===,
∵S菱形ABCD=×AC×BD=AB×CE,
∴4=×CE,
∴CE=,
∵∠OFC=∠AEC=90°,∠ACE=∠OCF,
∴△OCF∽△ACE,
∴,
∴CE=2CF,
∴CF=EF=,
∴OF===,
故答案为:.
20.(1)证明:∵四边形ABCD和EFCG均为正方形,
∴∠ABC=∠EFC=90°,
∵=k,
∴△ABC∽△EFC,
∴=,∠ACB=∠ECF,
∴=,∠ACE=∠BCF,
∴△CAE∽△CBF;
(2)解:∵△CAE∽△CBF,
∴=,
∵=k,
∴AB=kBC,
∴AC===BC,
∴=,
∴==,
∵AE=4,
∴BF=,
∵∠CAE+∠CBE=90°.∠CAE=∠CBF,
∴∠CBF+∠CBE=90°.
∴∠EBF=90°,
∴EF2=EB2+BF2=22+=4+,
∵=k,
∴FC=EF,
∴CE===EF,
∴CE2=(1+)(4+)=36,
解得k=±(负值舍去),
∴k=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
