选修3-4 11.3 简谐运动的回复力和能量 同步练习(word含答案)
文档属性
| 名称 | 选修3-4 11.3 简谐运动的回复力和能量 同步练习(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 383.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-24 00:00:00 | ||
图片预览


文档简介
选修3-4 11.3 简谐运动的回复力和能量 同步练习
一、单项选择题(共10小题;共40分)
1. 如图, 为平衡位置,小球在 、 间做无摩擦往复运动。由 向 运动的过程中,振子的
A. 动能增大,势能增大 B. 动能减小,势能增大
C. 动能增大,势能减小 D. 动能减小,势能减小
2. 简谐运动属于
A. 匀变速运动 B. 匀速直线运动
C. 变加速运动 D. 匀加速直线运动
3. 一弹簧振子做简谐运动时,其加速度随振动位移变化的图象应为
A. B.
C. D.
4. 如图甲所示,光滑水平杆上套着一个小球和一个弹簧,弹簧一端固定,另一端连接在小球上,忽略弹簧质量。小球以点 为平衡位置,在 、 两点之间做往复运动,它所受的回复力 随时间 变化的图象如图乙,则在 的时间内,小球的动能 和势能 的变化情况是
A. 变小, 变大 B. 变大, 变小
C. 、 均变小。 D. 、 均变大
5. 两个完全相同的弹簧振子 、 ,把 振子移到 的平衡位置右边 处,把 振子移到 的平衡位置左边 处,然后同时放手,下列说法正确的是
A. 振子在平衡位置的速度比 振子在平衡位置的速度小
B. 、 振子运动的方向有时相同、有时相反
C. 、 振子运动的方向总是相反的
D. 振子振动周期是 振子振动周期的 倍
6. 如图所示,物体 、 叠放在光滑水平面上,轻质弹簧的一端固定在墙面上,另一端与 相连,弹簧的轴线与水平面平行。开始时弹簧处于伸长状态,释放后物体 、 一起运动,从它们第一次向右通过平衡位置时开始计时,取向右为正方向,则物体 受到的摩擦力 与时间 的关系图象正确的是
A. B.
C. D.
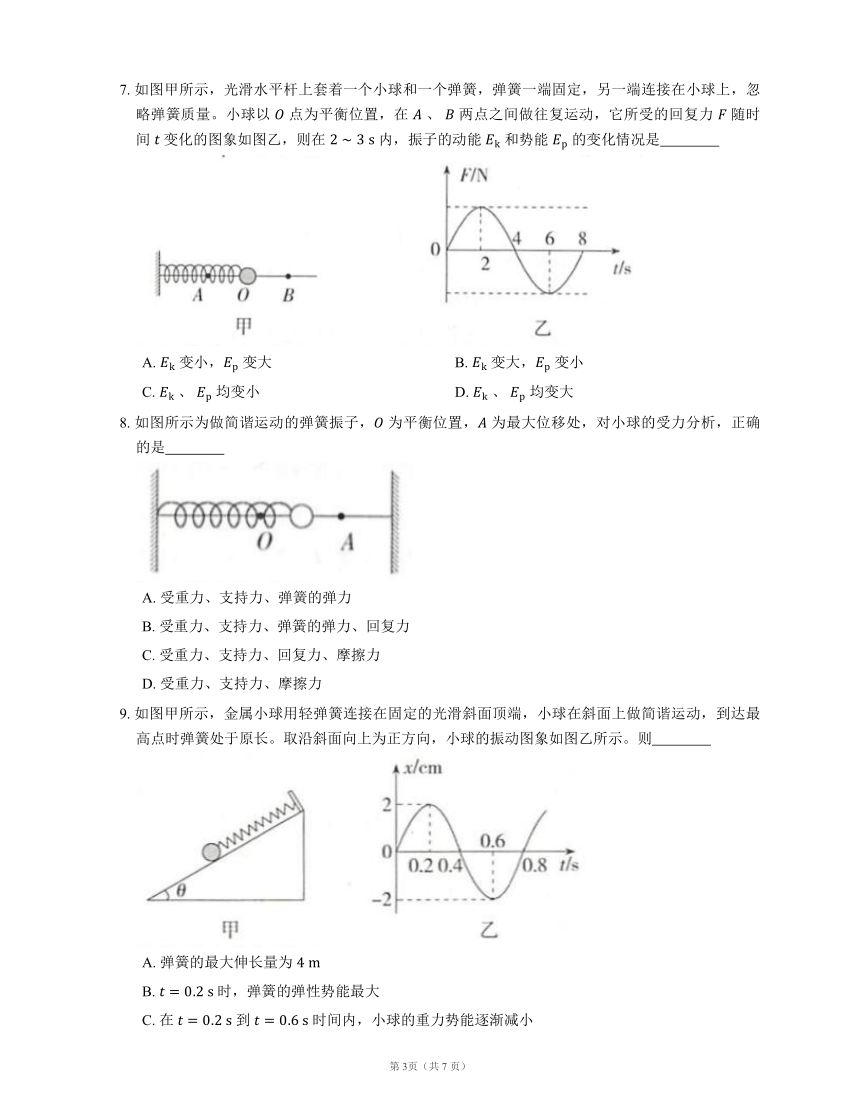
7. 如图甲所示,光滑水平杆上套着一个小球和一个弹簧,弹簧一端固定,另一端连接在小球上,忽略弹簧质量。小球以 点为平衡位置,在 、 两点之间做往复运动,它所受的回复力 随时间 变化的图象如图乙,则在 内,振子的动能 和势能 的变化情况是
A. 变小, 变大 B. 变大, 变小
C. 、 均变小 D. 、 均变大
8. 如图所示为做简谐运动的弹簧振子, 为平衡位置, 为最大位移处,对小球的受力分析,正确的是
A. 受重力、支持力、弹簧的弹力
B. 受重力、支持力、弹簧的弹力、回复力
C. 受重力、支持力、回复力、摩擦力
D. 受重力、支持力、摩擦力
9. 如图甲所示,金属小球用轻弹簧连接在固定的光滑斜面顶端,小球在斜面上做简谐运动,到达最高点时弹簧处于原长。取沿斜面向上为正方向,小球的振动图象如图乙所示。则
A. 弹簧的最大伸长量为
B. 时,弹簧的弹性势能最大
C. 在 到 时间内,小球的重力势能逐渐减小
D. 在 到 时间内,回复力的冲量为零
10. 弹簧振子的质量为 ,弹簧劲度系数为 ,在振子上放一质量为 的木块,使两者一起振动,如图所示。木块的回复力 是振子对木块的摩擦力, 也满足 , 是弹簧的伸长(或压缩)量,那么 为
A. B. C. D.
二、填空题(共4小题;共20分)
11. 简谐运动的质点通过平衡位置时,具有最大值的物理量是
A. 加速度 B. 速度 C. 位移 D. 动能 E. 回复力 F. 势能
12. 如图所示,一轻弹簧一端固定,另一端连接物块构成弹簧振子,该物块是由 、 两个小物块粘在一起组成的。物块在光滑水平面上左右振动,振幅为 ,周期为 ,当物块向右通过平衡位置时, 、 之间的粘胶脱开,以后小物块 振动的振幅和周期分别为 和 ,则 (选填“”“”或“”), (选填“”或“”)。
13. 如图所示,轻质弹簧一端固定在墙上,一质量为 的滑块以 的速度沿光滑水平面向左运动与弹簧相碰,弹簧被压缩,则此系统的最大弹性势能为 。当滑块压缩弹簧速度减为 时,此时系统的弹性势能为 。
14. 如图给出两个弹簧振子 、 做简谐运动的图象,则在 内 的速度方向沿 ,大小在逐渐 ;而 在这段时间内,其加速方向沿 ,大小在逐渐 。在 时, 、 振子通过平衡位置,并且它们的速度大小相等、方向相反,从此时起,再经过 的时间,它们再同时通过平衡位置且速度相同。
三、解答题(共3小题;共39分)
15. 如图所示为一水平放置的弹簧振子的振动图象,如果振子的质量为 ,则从计时开始经多长时间系统第一次达到弹性势能最大值 在第 末到第 末这段时间内弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的
16. 如图所示,质量均为 的物体 、 分别与轻质弹簧的两端相连接,将它们放在倾角为 的光滑斜面上,斜面底端有固定挡板 ,物体 靠在挡板 上。将质量也为 的物体 从斜面上的某点由静止释放, 与 相碰。已知重力加速度为 ,弹簧始终处于弹性限度内,不计空气阻力。若 与 相碰后粘连在一起开始做简谐运动,当 与 第一次运动到最高点时, 对挡板 的压力恰好为零,求 对挡板 压力的最大值。
17. 在水平光滑的细直角槽中嵌入两个质量相等的小物体 和 ,如图所示,它们之间用一长为 、质量可以忽略的刚性细杆铰接,铰接处在 、 滑动时可自由转动。已知当细杆与 轴的夹角为 时, 有一个沿 轴负方向的速度 ,试证明:
(1)细杆中点 将做圆周运动
(2) 、 各自做简谐运动,且用 、 、 来表示两物体的运动周期
答案
第一部分
1. C
【解析】由题意可知, 向 运动的过程中,振子机械能守恒,弹力做正功,所以振子势能减小,动能增大,故C正确,ABD错误。
2. C
【解析】根据简谐运动的特征 ,可知物体的加速度大小和方向随位移的变化而变化,位移做周期性变化,加速度也做周期性变化,所以简谐运动是变加速运动,故C正确,A、B、D错误。
3. C
【解析】由 知加速度与 ,因 和 一定,则加速度与位移的关系为正比例关系,比例系数为负,故选C。
4. B
【解析】在 的时间内,小球的回复力减小,则小球向平衡位置运动,速度变大。动能 变大,弹性势能 减小。
5. C
【解析】由于 、 是完全相同的弹簧振子,它们振动的周期相同,相位相差 ,所以 、 运动的方向总是相反的,故C正确,B 、D错误; 振子的振幅大于 振子的振幅,所以弹簧振子 的机械能大于弹簧振子 的机械能,由机械能守恒得, 振子在平衡位置的速度比 振子在平衡位置的速度大,故A错误。
6. A
【解析】物体 做简谐运动,其回复力就是 对它的摩擦力,这个摩擦力随时间按正弦规律变化,则物体 受到的摩擦力 也随时间按正弦规律变化,故选A。
7. B
【解析】由题图乙可知,在 内,小球所受回复力减小,则小球向平衡位置运动,速度变大,可知动能 变大,势能 减小。
8. A
【解析】小球受重力、支持力和弹簧的弹力,不受摩擦力,回复力是效果力,由弹簧弹力提供。
9. C
【解析】小球的振幅等于其位移的最大值,由图乙读出,振幅为 ,由于小球到达最高点时弹簧处于原长,所以弹簧的最大伸长量为 ,A错误;由图可知 时,弹簧处于原长,弹簧的弹性势能最小,为零,B错误;在 到 时间内,小球在沿斜面向下运动,小球的重力势能逐渐减小,C正确; 时小球经过平衡位置沿斜面向上运动, 时小球经过平衡位置沿斜面向下运动,根据动量定理可知回复力的冲量不为零,D错误。
10. B
第二部分
11. BD
12. ;
【解析】当物块向右通过平衡位置时, 、 之间的粘胶脱开,振子的质量减小,速度不突变,弹簧振子的机械能减小,振幅减小,则有 ;对于弹簧振子,其做简谐运动的周期取决于振子的质量以及弹簧的劲度系数,可知振子的质量减小,周期一定改变,则有 。
13. ;
【解析】全过程机械能守恒,由 ,得 ,当 时,。
14. 负方向;增大;正方向;减小;
第三部分
15. ;加速度增大,速度减小,动能减小,弹性势能增大
16.
【解析】 与 碰后一起做简谐运动,运动到最高点时,物体 对挡板 的压力恰好为 ,
则对 ,弹簧弹力:
对 、 ,回复力最大:
与 碰后一起做简谐运动,由简谐运动的对称性,可知运动到最低点时,回复力也最大,即
此时物体 对挡板 的压力最大,对物体 、 有
则弹簧弹力:
对物体 ,设挡板 对物体 的弹力为 ,则
由牛顿第三定律可知,物体 对挡板 的压力大小 ,故物体 对挡板 压力的最大值为 。
17. (1) 设 点坐标为 ,则有 ,这说明 点的轨迹是一个半径为 的圆
(2)
【解析】因为杆不可压缩,所以 和 沿杆方向的分量应相等,即 , 。对 、 组成的系统来说机械能守恒 (常数),其中 , ,故 (常数)。 作匀速圆周运动,故 、 均为简谐运动。由于 ,
第1页(共1 页)
一、单项选择题(共10小题;共40分)
1. 如图, 为平衡位置,小球在 、 间做无摩擦往复运动。由 向 运动的过程中,振子的
A. 动能增大,势能增大 B. 动能减小,势能增大
C. 动能增大,势能减小 D. 动能减小,势能减小
2. 简谐运动属于
A. 匀变速运动 B. 匀速直线运动
C. 变加速运动 D. 匀加速直线运动
3. 一弹簧振子做简谐运动时,其加速度随振动位移变化的图象应为
A. B.
C. D.
4. 如图甲所示,光滑水平杆上套着一个小球和一个弹簧,弹簧一端固定,另一端连接在小球上,忽略弹簧质量。小球以点 为平衡位置,在 、 两点之间做往复运动,它所受的回复力 随时间 变化的图象如图乙,则在 的时间内,小球的动能 和势能 的变化情况是
A. 变小, 变大 B. 变大, 变小
C. 、 均变小。 D. 、 均变大
5. 两个完全相同的弹簧振子 、 ,把 振子移到 的平衡位置右边 处,把 振子移到 的平衡位置左边 处,然后同时放手,下列说法正确的是
A. 振子在平衡位置的速度比 振子在平衡位置的速度小
B. 、 振子运动的方向有时相同、有时相反
C. 、 振子运动的方向总是相反的
D. 振子振动周期是 振子振动周期的 倍
6. 如图所示,物体 、 叠放在光滑水平面上,轻质弹簧的一端固定在墙面上,另一端与 相连,弹簧的轴线与水平面平行。开始时弹簧处于伸长状态,释放后物体 、 一起运动,从它们第一次向右通过平衡位置时开始计时,取向右为正方向,则物体 受到的摩擦力 与时间 的关系图象正确的是
A. B.
C. D.
7. 如图甲所示,光滑水平杆上套着一个小球和一个弹簧,弹簧一端固定,另一端连接在小球上,忽略弹簧质量。小球以 点为平衡位置,在 、 两点之间做往复运动,它所受的回复力 随时间 变化的图象如图乙,则在 内,振子的动能 和势能 的变化情况是
A. 变小, 变大 B. 变大, 变小
C. 、 均变小 D. 、 均变大
8. 如图所示为做简谐运动的弹簧振子, 为平衡位置, 为最大位移处,对小球的受力分析,正确的是
A. 受重力、支持力、弹簧的弹力
B. 受重力、支持力、弹簧的弹力、回复力
C. 受重力、支持力、回复力、摩擦力
D. 受重力、支持力、摩擦力
9. 如图甲所示,金属小球用轻弹簧连接在固定的光滑斜面顶端,小球在斜面上做简谐运动,到达最高点时弹簧处于原长。取沿斜面向上为正方向,小球的振动图象如图乙所示。则
A. 弹簧的最大伸长量为
B. 时,弹簧的弹性势能最大
C. 在 到 时间内,小球的重力势能逐渐减小
D. 在 到 时间内,回复力的冲量为零
10. 弹簧振子的质量为 ,弹簧劲度系数为 ,在振子上放一质量为 的木块,使两者一起振动,如图所示。木块的回复力 是振子对木块的摩擦力, 也满足 , 是弹簧的伸长(或压缩)量,那么 为
A. B. C. D.
二、填空题(共4小题;共20分)
11. 简谐运动的质点通过平衡位置时,具有最大值的物理量是
A. 加速度 B. 速度 C. 位移 D. 动能 E. 回复力 F. 势能
12. 如图所示,一轻弹簧一端固定,另一端连接物块构成弹簧振子,该物块是由 、 两个小物块粘在一起组成的。物块在光滑水平面上左右振动,振幅为 ,周期为 ,当物块向右通过平衡位置时, 、 之间的粘胶脱开,以后小物块 振动的振幅和周期分别为 和 ,则 (选填“”“”或“”), (选填“”或“”)。
13. 如图所示,轻质弹簧一端固定在墙上,一质量为 的滑块以 的速度沿光滑水平面向左运动与弹簧相碰,弹簧被压缩,则此系统的最大弹性势能为 。当滑块压缩弹簧速度减为 时,此时系统的弹性势能为 。
14. 如图给出两个弹簧振子 、 做简谐运动的图象,则在 内 的速度方向沿 ,大小在逐渐 ;而 在这段时间内,其加速方向沿 ,大小在逐渐 。在 时, 、 振子通过平衡位置,并且它们的速度大小相等、方向相反,从此时起,再经过 的时间,它们再同时通过平衡位置且速度相同。
三、解答题(共3小题;共39分)
15. 如图所示为一水平放置的弹簧振子的振动图象,如果振子的质量为 ,则从计时开始经多长时间系统第一次达到弹性势能最大值 在第 末到第 末这段时间内弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的
16. 如图所示,质量均为 的物体 、 分别与轻质弹簧的两端相连接,将它们放在倾角为 的光滑斜面上,斜面底端有固定挡板 ,物体 靠在挡板 上。将质量也为 的物体 从斜面上的某点由静止释放, 与 相碰。已知重力加速度为 ,弹簧始终处于弹性限度内,不计空气阻力。若 与 相碰后粘连在一起开始做简谐运动,当 与 第一次运动到最高点时, 对挡板 的压力恰好为零,求 对挡板 压力的最大值。
17. 在水平光滑的细直角槽中嵌入两个质量相等的小物体 和 ,如图所示,它们之间用一长为 、质量可以忽略的刚性细杆铰接,铰接处在 、 滑动时可自由转动。已知当细杆与 轴的夹角为 时, 有一个沿 轴负方向的速度 ,试证明:
(1)细杆中点 将做圆周运动
(2) 、 各自做简谐运动,且用 、 、 来表示两物体的运动周期
答案
第一部分
1. C
【解析】由题意可知, 向 运动的过程中,振子机械能守恒,弹力做正功,所以振子势能减小,动能增大,故C正确,ABD错误。
2. C
【解析】根据简谐运动的特征 ,可知物体的加速度大小和方向随位移的变化而变化,位移做周期性变化,加速度也做周期性变化,所以简谐运动是变加速运动,故C正确,A、B、D错误。
3. C
【解析】由 知加速度与 ,因 和 一定,则加速度与位移的关系为正比例关系,比例系数为负,故选C。
4. B
【解析】在 的时间内,小球的回复力减小,则小球向平衡位置运动,速度变大。动能 变大,弹性势能 减小。
5. C
【解析】由于 、 是完全相同的弹簧振子,它们振动的周期相同,相位相差 ,所以 、 运动的方向总是相反的,故C正确,B 、D错误; 振子的振幅大于 振子的振幅,所以弹簧振子 的机械能大于弹簧振子 的机械能,由机械能守恒得, 振子在平衡位置的速度比 振子在平衡位置的速度大,故A错误。
6. A
【解析】物体 做简谐运动,其回复力就是 对它的摩擦力,这个摩擦力随时间按正弦规律变化,则物体 受到的摩擦力 也随时间按正弦规律变化,故选A。
7. B
【解析】由题图乙可知,在 内,小球所受回复力减小,则小球向平衡位置运动,速度变大,可知动能 变大,势能 减小。
8. A
【解析】小球受重力、支持力和弹簧的弹力,不受摩擦力,回复力是效果力,由弹簧弹力提供。
9. C
【解析】小球的振幅等于其位移的最大值,由图乙读出,振幅为 ,由于小球到达最高点时弹簧处于原长,所以弹簧的最大伸长量为 ,A错误;由图可知 时,弹簧处于原长,弹簧的弹性势能最小,为零,B错误;在 到 时间内,小球在沿斜面向下运动,小球的重力势能逐渐减小,C正确; 时小球经过平衡位置沿斜面向上运动, 时小球经过平衡位置沿斜面向下运动,根据动量定理可知回复力的冲量不为零,D错误。
10. B
第二部分
11. BD
12. ;
【解析】当物块向右通过平衡位置时, 、 之间的粘胶脱开,振子的质量减小,速度不突变,弹簧振子的机械能减小,振幅减小,则有 ;对于弹簧振子,其做简谐运动的周期取决于振子的质量以及弹簧的劲度系数,可知振子的质量减小,周期一定改变,则有 。
13. ;
【解析】全过程机械能守恒,由 ,得 ,当 时,。
14. 负方向;增大;正方向;减小;
第三部分
15. ;加速度增大,速度减小,动能减小,弹性势能增大
16.
【解析】 与 碰后一起做简谐运动,运动到最高点时,物体 对挡板 的压力恰好为 ,
则对 ,弹簧弹力:
对 、 ,回复力最大:
与 碰后一起做简谐运动,由简谐运动的对称性,可知运动到最低点时,回复力也最大,即
此时物体 对挡板 的压力最大,对物体 、 有
则弹簧弹力:
对物体 ,设挡板 对物体 的弹力为 ,则
由牛顿第三定律可知,物体 对挡板 的压力大小 ,故物体 对挡板 压力的最大值为 。
17. (1) 设 点坐标为 ,则有 ,这说明 点的轨迹是一个半径为 的圆
(2)
【解析】因为杆不可压缩,所以 和 沿杆方向的分量应相等,即 , 。对 、 组成的系统来说机械能守恒 (常数),其中 , ,故 (常数)。 作匀速圆周运动,故 、 均为简谐运动。由于 ,
第1页(共1 页)
