选修3-4 13.2 全反射 同步练习(word含答案)
文档属性
| 名称 | 选修3-4 13.2 全反射 同步练习(word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 440.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-24 00:00:00 | ||
图片预览



文档简介
选修3-4 13.2 全反射 同步练习
一、单项选择题(共10小题;共40分)
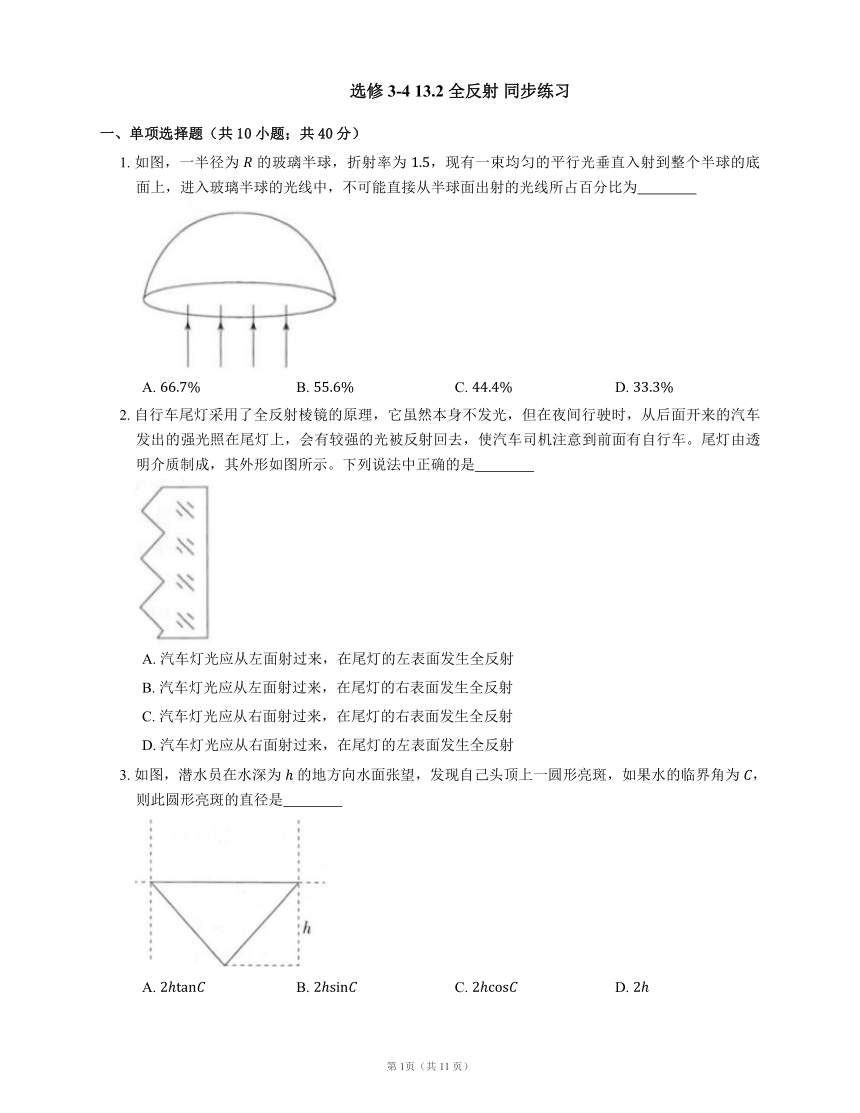
1. 如图,一半径为 的玻璃半球,折射率为 ,现有一束均匀的平行光垂直入射到整个半球的底面上,进入玻璃半球的光线中,不可能直接从半球面出射的光线所占百分比为
A. B. C. D.
2. 自行车尾灯采用了全反射棱镜的原理,它虽然本身不发光,但在夜间行驶时,从后面开来的汽车发出的强光照在尾灯上,会有较强的光被反射回去,使汽车司机注意到前面有自行车。尾灯由透明介质制成,其外形如图所示。下列说法中正确的是
A. 汽车灯光应从左面射过来,在尾灯的左表面发生全反射
B. 汽车灯光应从左面射过来,在尾灯的右表面发生全反射
C. 汽车灯光应从右面射过来,在尾灯的右表面发生全反射
D. 汽车灯光应从右面射过来,在尾灯的左表面发生全反射
3. 如图,潜水员在水深为 的地方向水面张望,发现自己头顶上一圆形亮斑,如果水的临界角为 ,则此圆形亮斑的直径是
A. B. C. D.
4. 回归反光膜是由高折射率透明陶瓷圆珠、高强度黏合剂等组成的复合型薄膜材料。在夜间,它能使各种角度车灯射出的光线逆向返回,使标志牌上的字特别醒目。一束平行光(宽度远大于陶瓷圆珠直径和圆珠间距)沿垂直基板方向照射到圆珠上,为使折射入陶瓷圆珠的光能发生全反射,则制作陶瓷圆珠材料的折射率 至少为
A. B. C. D.
5. 在桌面上有一倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示。有一半径为 的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为 ,则光束在桌面上形成的光斑半径为
A. B. C. D.
6. 光在某种介质中传播的速度为 ,光从此介质射向空气并发生全反射时的临界角是
A. B. C. D.
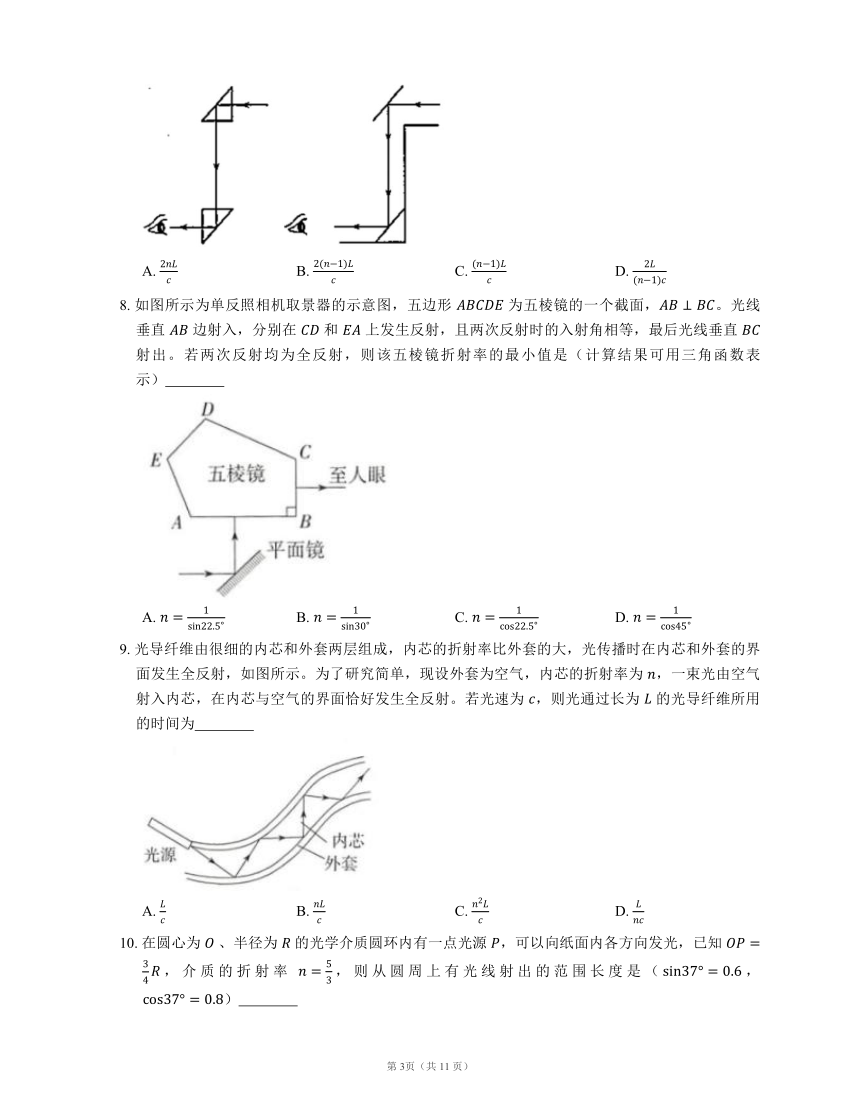
7. 作为中国海军发展的第二代核潜艇, 核潜艇虽然性能不及西方先进核潜艇,但火力十分强悍,已经搭载了中国最新研制的“巨浪 ”潜射弹道导弹,打击射程达到 公里。作为一种用来携带并发射潜射洲际导弹的战略核潜艇,是中国三位一体中核力量的重要组成部分,也是目前中国军队中生存能力最强的核装备,肩负着中国的二次反击的重任。在浅水中航行的潜艇为了观察水面情况,常使用潜望镜。潜望镜有些是用两个相同的全反射棱镜(截面为等腰直角三角形)制成,有些是用两个平面镜(厚度不计)制成,平面镜和全反射棱镜安装在潜望镜的同一位置,光路如图所示。已知某潜望镜用的全反射棱镜的直角边长为 ,折射率为 ,在矿泉水中的波长为 ,真空中的光速为 。对于该潜望镜,用全反射棱镜与用平面镜,光线通过潜望镜的时间差为
A. B. C. D.
8. 如图所示为单反照相机取景器的示意图,五边形 为五棱镜的一个截面,。光线垂直 边射入,分别在 和 上发生反射,且两次反射时的入射角相等,最后光线垂直 射出。若两次反射均为全反射,则该五棱镜折射率的最小值是(计算结果可用三角函数表示)
A. B. C. D.
9. 光导纤维由很细的内芯和外套两层组成,内芯的折射率比外套的大,光传播时在内芯和外套的界面发生全反射,如图所示。为了研究简单,现设外套为空气,内芯的折射率为 ,一束光由空气射入内芯,在内芯与空气的界面恰好发生全反射。若光速为 ,则光通过长为 的光导纤维所用的时间为
A. B. C. D.
10. 在圆心为 、半径为 的光学介质圆环内有一点光源 ,可以向纸面内各方向发光,已知 ,介质的折射率 ,则从圆周上有光线射出的范围长度是(,)
A. B. C. D.
二、填空题(共4小题;共18分)
11. 光纤通信中,光导纤维传递光信号的物理原理是利用光的全反射现象,要发生这种现象,必须满足的条件是:光的入射方向应该是 (填“从光密介质到光疏介质”或“从光疏介质到光密介质”),且入射角 临界角(填“”或“”)。
12. 在北方寒冷的冬天,有时会出现“多个太阳”的“幻日”奇观,这是空气中的水蒸气在极冷的大气里凝结成了小冰晶,太阳光通过小冰晶发生折射的缘故。如图所示为太阳光照射到六边形冰晶上发生折射的光路图, 、 是太阳光中的两种单色光,由此可以判断,冰晶对单色光 的折射率 (填“大于”或“小于”)冰晶对单色光 的折射率,单色光 在冰晶中的传播速度比单色光 在冰晶中的传播速度 (填“大”或“小”)。如果让太阳光从冰晶射向空气,逐渐增大入射角,则 、 两种单色光中,单色光 (填“”或“”)更容易发生全反射。
13. 水的折射率 ,当在水面下 深处放一强点光源时,看到透光水面的最大直径是 。当此透光水面的直径变大时,光源正在 (选填“上浮”或下沉”)。
14. 宽为 、中央水深为 的池塘边有一棵树,站在正对岸边的人看到树顶端的倒影与池塘底部中央的点光源在一条直线上。已知人眼到水面的高度为 ,树顶端到水面的高度为 ,则水的折射率为 。若在水面上各处都看不到该光,则至少要在水面上铺设直径为 的遮光膜。(结果可用根号表示)
三、解答题(共3小题;共39分)
15. 如图,一长方体透明玻璃砖在底部挖去半径为 的半圆柱,玻璃砖长为 。一束单色光垂直于玻璃砖上表面射入玻璃砖,且覆盖玻璃砖整个上表面,已知该单色光在玻璃砖中的折射率为 ,真空中的光速 ,不考虑光在玻璃砖中的多次反射。求:
(1)单色光在玻璃砖中的传播速度(结果保留 位小数);
(2)半圆柱面上有光线射出的表面积。
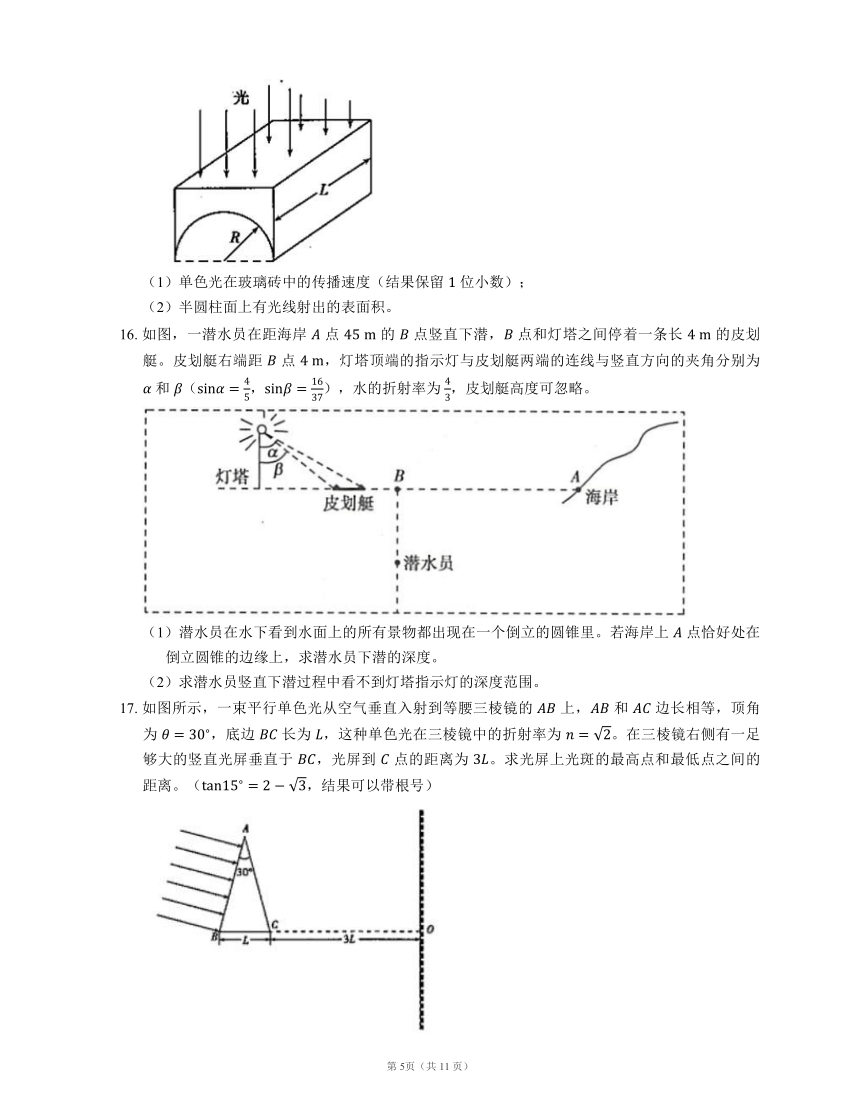
16. 如图,一潜水员在距海岸 点 的 点竖直下潜, 点和灯塔之间停着一条长 的皮划艇。皮划艇右端距 点 ,灯塔顶端的指示灯与皮划艇两端的连线与竖直方向的夹角分别为 和 (,),水的折射率为 ,皮划艇高度可忽略。
(1)潜水员在水下看到水面上的所有景物都出现在一个倒立的圆锥里。若海岸上 点恰好处在倒立圆锥的边缘上,求潜水员下潜的深度。
(2)求潜水员竖直下潜过程中看不到灯塔指示灯的深度范围。
17. 如图所示,一束平行单色光从空气垂直入射到等腰三棱镜的 上, 和 边长相等,顶角为 ,底边 长为 ,这种单色光在三棱镜中的折射率为 。在三棱镜右侧有一足够大的竖直光屏垂直于 ,光屏到 点的距离为 。求光屏上光斑的最高点和最低点之间的距离。(,结果可以带根号)
答案
第一部分
1. B
【解析】如图,假设从 点入射的光在半球面的 点刚好发生全反射,则从以 为圆心、 长为半径的圆范围外射入的光线不能直接从半球面射出,,,所以能直接从半球面射出的光线占比为 ,则不能直接从半球面射出的光线所占百分比为 ,故选B。
2. D
【解析】自行车尾灯利用了全反射原理,汽车灯光应从右面射过来,在左表面发生两次全反射被反射回去。
3. A
【解析】在圆形亮斑边缘,从空气射入水中的光线,折射角的大小等于临界角 ,如图所示,由几何关系可知,圆形亮斑的直径 ,故A正确,B、C、D错误。
4. B
【解析】考虑临界情况,光路如图所示,
设折射角为 ,
则有 ,
由几何关系可得 ,
解得 ,
故选B。
5. C
【解析】光线会发生全反射,光路图如图,
由图中几何关系可得 ,故 。
6. B
【解析】根据折射定律,有折射率
正好发生全反射,则有
解得 ,故选B。
7. B
【解析】两种情况下总的光程相等,只是用全反射棱镜时,光会在玻璃中传播一段距离,,相应的时间 ,
其中 ,
而用平面镜时,对应的 的光程是在空气中进行的,,
时间差为 。
8. A
【解析】设入射到 上的入射角为 ,因为在 和 上发生反射,且两次反射的入射角相等,根据几何关系有 ,解得 ;根据 ,解得五棱镜的最小折射率为 ,A正确,B、C、D错误。
9. C
【解析】一束光由空气射入内芯,在内芯与空气的界面恰好发生全反射,设临界角为 ,则光的传播方向与光导纤维之间的夹角为 ,光通过长为 的光导纤维时的路程 ;内芯的折射率为 ,则光在光导纤维中的传播速度 ,又由于 ,所以光的传播时间 ,故选C
10. B
第二部分
11. 从光密介质到光疏介质;
【解析】发生全反射的条件是光从光密介质进入光疏介质,且入射角大于等于临界角。
12. 小于;大;
【解析】光从空气斜射到冰晶上,由题图可知,单色光 偏折较大,单色光 偏折较小,所以此冰晶对单色光 的折射率小于对单色光 的折射率;根据 可知单色光 在冰晶中的传播速度比单色光 在冰晶中的传播速度大。根据 知单色光 的临界角较小,所以单色光 比单色光 更容易发生全反射。
13. ;下沉
14. ;
【解析】根据题意画出光路图如图所示:
,,,,由几何关系知 ,,,,则水的折射率 ;光从水中射入空气中,当入射角大于或等于临界角时发生全反射,设临界角为 ,则 ;设遮光膜半径为 ,,解得 ,所以遮光膜的最小直径 。
第三部分
15. (1)
【解析】由公式 得单色光在玻璃砖中的传播速度 。
(2)
【解析】光线经过玻璃砖上表面到达下方的半圆柱面出射时可能发生全反射,如图
设发生全反射的临界角为 ,由
则有光线射出的部分圆柱面的面积为
得 。
16. (1)
【解析】设潜水员下潜到 点时,由 点发出的光线恰好在 点发生全反射,临界角为 ,
则有 ,
,
。
(2)
【解析】由折射定律,灯塔发出的光恰好照到皮划艇右沿外侧并射入水中时,
,
,
可得 ,
同理,灯塔发出的光恰好照到皮划艇左沿外侧并射入水中时
,
,
可得 ,
则潜水员看不到灯塔指示灯的深度范围为 。
17.
【解析】根据全反射条件,光线射入三棱镜后射出时的临界角
光线射入三棱镜后,在 边的入射角为 ,不会发生全反射
设射出 边时的出射角为 ,根据折射定律有
得
根据题意可知,射到光屏上最低点的位置在图中 点,如图所示由几何关系可知
故
在 边的入射角为 ,大于全反射的临界角 ,会发生全反射。
由题意可知,从 边全反射的光线中射到光屏上最高点的位置在图中 点,如图所示。由几何关系可知,
故
所以光屏上光斑的最高点和最低点之间的距离为 。
第1页(共1 页)
一、单项选择题(共10小题;共40分)
1. 如图,一半径为 的玻璃半球,折射率为 ,现有一束均匀的平行光垂直入射到整个半球的底面上,进入玻璃半球的光线中,不可能直接从半球面出射的光线所占百分比为
A. B. C. D.
2. 自行车尾灯采用了全反射棱镜的原理,它虽然本身不发光,但在夜间行驶时,从后面开来的汽车发出的强光照在尾灯上,会有较强的光被反射回去,使汽车司机注意到前面有自行车。尾灯由透明介质制成,其外形如图所示。下列说法中正确的是
A. 汽车灯光应从左面射过来,在尾灯的左表面发生全反射
B. 汽车灯光应从左面射过来,在尾灯的右表面发生全反射
C. 汽车灯光应从右面射过来,在尾灯的右表面发生全反射
D. 汽车灯光应从右面射过来,在尾灯的左表面发生全反射
3. 如图,潜水员在水深为 的地方向水面张望,发现自己头顶上一圆形亮斑,如果水的临界角为 ,则此圆形亮斑的直径是
A. B. C. D.
4. 回归反光膜是由高折射率透明陶瓷圆珠、高强度黏合剂等组成的复合型薄膜材料。在夜间,它能使各种角度车灯射出的光线逆向返回,使标志牌上的字特别醒目。一束平行光(宽度远大于陶瓷圆珠直径和圆珠间距)沿垂直基板方向照射到圆珠上,为使折射入陶瓷圆珠的光能发生全反射,则制作陶瓷圆珠材料的折射率 至少为
A. B. C. D.
5. 在桌面上有一倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示。有一半径为 的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为 ,则光束在桌面上形成的光斑半径为
A. B. C. D.
6. 光在某种介质中传播的速度为 ,光从此介质射向空气并发生全反射时的临界角是
A. B. C. D.
7. 作为中国海军发展的第二代核潜艇, 核潜艇虽然性能不及西方先进核潜艇,但火力十分强悍,已经搭载了中国最新研制的“巨浪 ”潜射弹道导弹,打击射程达到 公里。作为一种用来携带并发射潜射洲际导弹的战略核潜艇,是中国三位一体中核力量的重要组成部分,也是目前中国军队中生存能力最强的核装备,肩负着中国的二次反击的重任。在浅水中航行的潜艇为了观察水面情况,常使用潜望镜。潜望镜有些是用两个相同的全反射棱镜(截面为等腰直角三角形)制成,有些是用两个平面镜(厚度不计)制成,平面镜和全反射棱镜安装在潜望镜的同一位置,光路如图所示。已知某潜望镜用的全反射棱镜的直角边长为 ,折射率为 ,在矿泉水中的波长为 ,真空中的光速为 。对于该潜望镜,用全反射棱镜与用平面镜,光线通过潜望镜的时间差为
A. B. C. D.
8. 如图所示为单反照相机取景器的示意图,五边形 为五棱镜的一个截面,。光线垂直 边射入,分别在 和 上发生反射,且两次反射时的入射角相等,最后光线垂直 射出。若两次反射均为全反射,则该五棱镜折射率的最小值是(计算结果可用三角函数表示)
A. B. C. D.
9. 光导纤维由很细的内芯和外套两层组成,内芯的折射率比外套的大,光传播时在内芯和外套的界面发生全反射,如图所示。为了研究简单,现设外套为空气,内芯的折射率为 ,一束光由空气射入内芯,在内芯与空气的界面恰好发生全反射。若光速为 ,则光通过长为 的光导纤维所用的时间为
A. B. C. D.
10. 在圆心为 、半径为 的光学介质圆环内有一点光源 ,可以向纸面内各方向发光,已知 ,介质的折射率 ,则从圆周上有光线射出的范围长度是(,)
A. B. C. D.
二、填空题(共4小题;共18分)
11. 光纤通信中,光导纤维传递光信号的物理原理是利用光的全反射现象,要发生这种现象,必须满足的条件是:光的入射方向应该是 (填“从光密介质到光疏介质”或“从光疏介质到光密介质”),且入射角 临界角(填“”或“”)。
12. 在北方寒冷的冬天,有时会出现“多个太阳”的“幻日”奇观,这是空气中的水蒸气在极冷的大气里凝结成了小冰晶,太阳光通过小冰晶发生折射的缘故。如图所示为太阳光照射到六边形冰晶上发生折射的光路图, 、 是太阳光中的两种单色光,由此可以判断,冰晶对单色光 的折射率 (填“大于”或“小于”)冰晶对单色光 的折射率,单色光 在冰晶中的传播速度比单色光 在冰晶中的传播速度 (填“大”或“小”)。如果让太阳光从冰晶射向空气,逐渐增大入射角,则 、 两种单色光中,单色光 (填“”或“”)更容易发生全反射。
13. 水的折射率 ,当在水面下 深处放一强点光源时,看到透光水面的最大直径是 。当此透光水面的直径变大时,光源正在 (选填“上浮”或下沉”)。
14. 宽为 、中央水深为 的池塘边有一棵树,站在正对岸边的人看到树顶端的倒影与池塘底部中央的点光源在一条直线上。已知人眼到水面的高度为 ,树顶端到水面的高度为 ,则水的折射率为 。若在水面上各处都看不到该光,则至少要在水面上铺设直径为 的遮光膜。(结果可用根号表示)
三、解答题(共3小题;共39分)
15. 如图,一长方体透明玻璃砖在底部挖去半径为 的半圆柱,玻璃砖长为 。一束单色光垂直于玻璃砖上表面射入玻璃砖,且覆盖玻璃砖整个上表面,已知该单色光在玻璃砖中的折射率为 ,真空中的光速 ,不考虑光在玻璃砖中的多次反射。求:
(1)单色光在玻璃砖中的传播速度(结果保留 位小数);
(2)半圆柱面上有光线射出的表面积。
16. 如图,一潜水员在距海岸 点 的 点竖直下潜, 点和灯塔之间停着一条长 的皮划艇。皮划艇右端距 点 ,灯塔顶端的指示灯与皮划艇两端的连线与竖直方向的夹角分别为 和 (,),水的折射率为 ,皮划艇高度可忽略。
(1)潜水员在水下看到水面上的所有景物都出现在一个倒立的圆锥里。若海岸上 点恰好处在倒立圆锥的边缘上,求潜水员下潜的深度。
(2)求潜水员竖直下潜过程中看不到灯塔指示灯的深度范围。
17. 如图所示,一束平行单色光从空气垂直入射到等腰三棱镜的 上, 和 边长相等,顶角为 ,底边 长为 ,这种单色光在三棱镜中的折射率为 。在三棱镜右侧有一足够大的竖直光屏垂直于 ,光屏到 点的距离为 。求光屏上光斑的最高点和最低点之间的距离。(,结果可以带根号)
答案
第一部分
1. B
【解析】如图,假设从 点入射的光在半球面的 点刚好发生全反射,则从以 为圆心、 长为半径的圆范围外射入的光线不能直接从半球面射出,,,所以能直接从半球面射出的光线占比为 ,则不能直接从半球面射出的光线所占百分比为 ,故选B。
2. D
【解析】自行车尾灯利用了全反射原理,汽车灯光应从右面射过来,在左表面发生两次全反射被反射回去。
3. A
【解析】在圆形亮斑边缘,从空气射入水中的光线,折射角的大小等于临界角 ,如图所示,由几何关系可知,圆形亮斑的直径 ,故A正确,B、C、D错误。
4. B
【解析】考虑临界情况,光路如图所示,
设折射角为 ,
则有 ,
由几何关系可得 ,
解得 ,
故选B。
5. C
【解析】光线会发生全反射,光路图如图,
由图中几何关系可得 ,故 。
6. B
【解析】根据折射定律,有折射率
正好发生全反射,则有
解得 ,故选B。
7. B
【解析】两种情况下总的光程相等,只是用全反射棱镜时,光会在玻璃中传播一段距离,,相应的时间 ,
其中 ,
而用平面镜时,对应的 的光程是在空气中进行的,,
时间差为 。
8. A
【解析】设入射到 上的入射角为 ,因为在 和 上发生反射,且两次反射的入射角相等,根据几何关系有 ,解得 ;根据 ,解得五棱镜的最小折射率为 ,A正确,B、C、D错误。
9. C
【解析】一束光由空气射入内芯,在内芯与空气的界面恰好发生全反射,设临界角为 ,则光的传播方向与光导纤维之间的夹角为 ,光通过长为 的光导纤维时的路程 ;内芯的折射率为 ,则光在光导纤维中的传播速度 ,又由于 ,所以光的传播时间 ,故选C
10. B
第二部分
11. 从光密介质到光疏介质;
【解析】发生全反射的条件是光从光密介质进入光疏介质,且入射角大于等于临界角。
12. 小于;大;
【解析】光从空气斜射到冰晶上,由题图可知,单色光 偏折较大,单色光 偏折较小,所以此冰晶对单色光 的折射率小于对单色光 的折射率;根据 可知单色光 在冰晶中的传播速度比单色光 在冰晶中的传播速度大。根据 知单色光 的临界角较小,所以单色光 比单色光 更容易发生全反射。
13. ;下沉
14. ;
【解析】根据题意画出光路图如图所示:
,,,,由几何关系知 ,,,,则水的折射率 ;光从水中射入空气中,当入射角大于或等于临界角时发生全反射,设临界角为 ,则 ;设遮光膜半径为 ,,解得 ,所以遮光膜的最小直径 。
第三部分
15. (1)
【解析】由公式 得单色光在玻璃砖中的传播速度 。
(2)
【解析】光线经过玻璃砖上表面到达下方的半圆柱面出射时可能发生全反射,如图
设发生全反射的临界角为 ,由
则有光线射出的部分圆柱面的面积为
得 。
16. (1)
【解析】设潜水员下潜到 点时,由 点发出的光线恰好在 点发生全反射,临界角为 ,
则有 ,
,
。
(2)
【解析】由折射定律,灯塔发出的光恰好照到皮划艇右沿外侧并射入水中时,
,
,
可得 ,
同理,灯塔发出的光恰好照到皮划艇左沿外侧并射入水中时
,
,
可得 ,
则潜水员看不到灯塔指示灯的深度范围为 。
17.
【解析】根据全反射条件,光线射入三棱镜后射出时的临界角
光线射入三棱镜后,在 边的入射角为 ,不会发生全反射
设射出 边时的出射角为 ,根据折射定律有
得
根据题意可知,射到光屏上最低点的位置在图中 点,如图所示由几何关系可知
故
在 边的入射角为 ,大于全反射的临界角 ,会发生全反射。
由题意可知,从 边全反射的光线中射到光屏上最高点的位置在图中 点,如图所示。由几何关系可知,
故
所以光屏上光斑的最高点和最低点之间的距离为 。
第1页(共1 页)
