北京课改版八下数学 第15章四边形 本章检测(word版含答案)
文档属性
| 名称 | 北京课改版八下数学 第15章四边形 本章检测(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 09:32:40 | ||
图片预览

文档简介
北京课改版八下数学 第15章四边形 本章检测
一、选择题(共10小题;共50分)
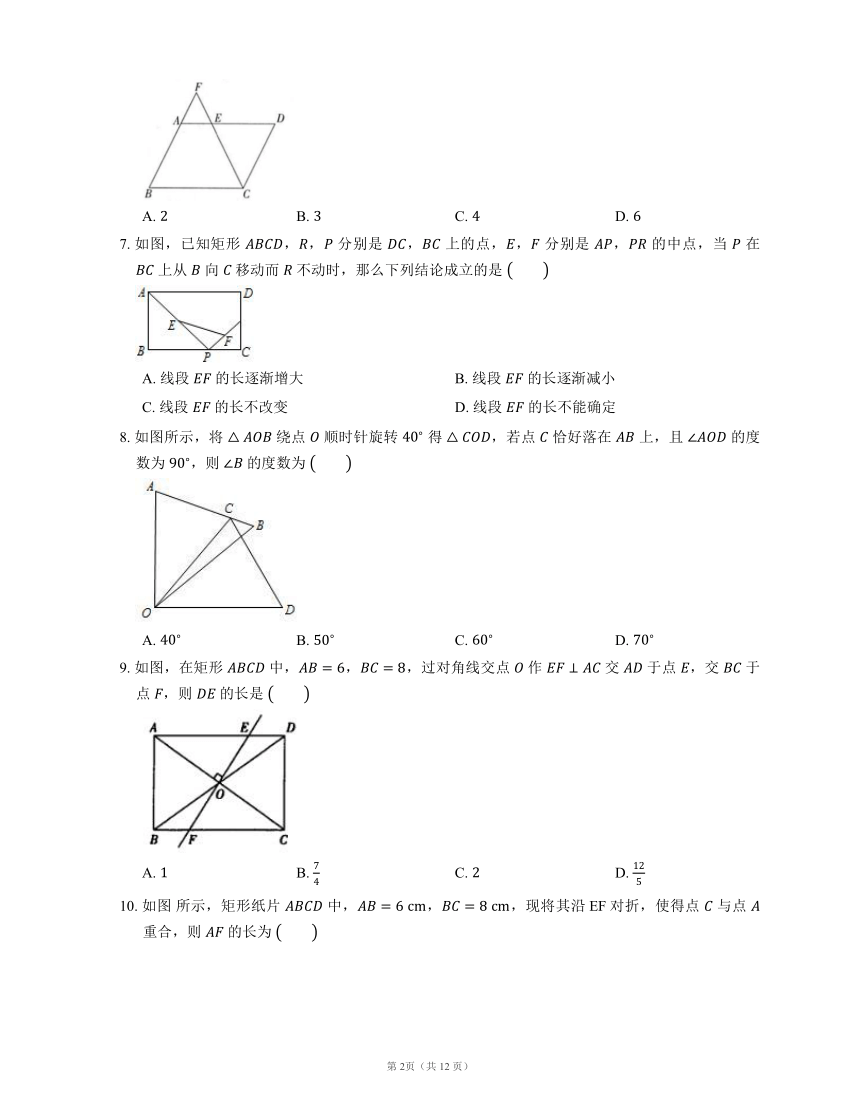
1. 如图,点 ,, 的坐标分别为 ,, 从下面四个点 , , , 中选择一个点,以 ,, 与该点为顶点的四边形不是中心对称图形,则该点是
A. B. C. D.
2. 如图所示的矩形 ,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为 和 ,则 不可能是
A. B. C. D.
3. 若三角形的三条中位线长分别为 ,,,则原三角形的周长为
A. B. C. D.
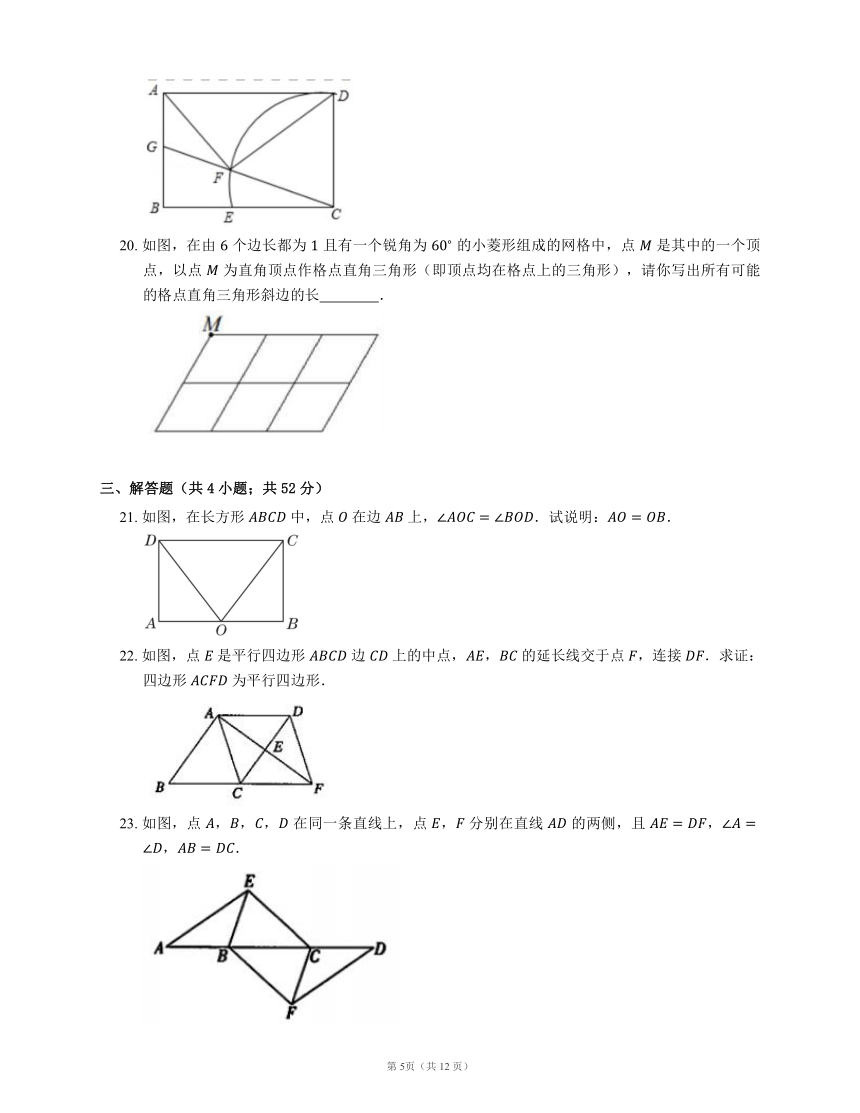
4. 如图,四边形 是菱形,,,则 的长是
A. B. C. D.
5. 下列图形中能够用来做平面镶嵌的图形的是
A. 正八边形 B. 正七边形 C. 正六边形 D. 正五边形
6. 如图,在平行四边形 中,,, 的平分线交 与点 ,交 的延长线于点 ,则 的值等于
A. B. C. D.
7. 如图,已知矩形 ,, 分别是 , 上的点,, 分别是 , 的中点,当 在 上从 向 移动而 不动时,那么下列结论成立的是
A. 线段 的长逐渐增大 B. 线段 的长逐渐减小
C. 线段 的长不改变 D. 线段 的长不能确定
8. 如图所示,将 绕点 顺时针旋转 得 ,若点 恰好落在 上,且 的度数为 ,则 的度数为
A. B. C. D.
9. 如图,在矩形 中,,,过对角线交点 作 交 于点 ,交 于点 ,则 的长是
A. B. C. D.
10. 如图 所示,矩形纸片 中,,,现将其沿EF对折,使得点 与点 重合,则 的长为
A. B. C. D.
二、填空题(共10小题;共50分)
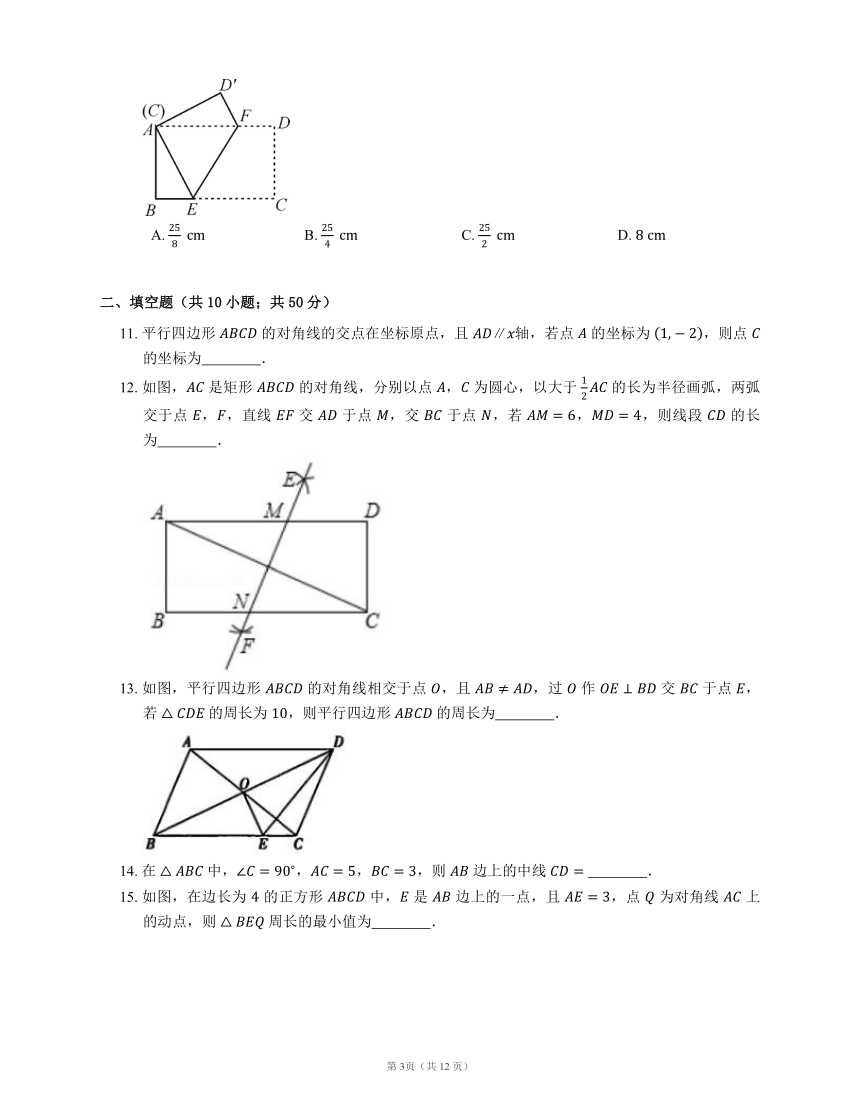
11. 平行四边形 的对角线的交点在坐标原点,且 ,若点 的坐标为 ,则点 的坐标为 .
12. 如图, 是矩形 的对角线,分别以点 , 为圆心,以大于 的长为半径画弧,两弧交于点 ,,直线 交 于点 ,交 于点 ,若 ,,则线段 的长为 .
13. 如图,平行四边形 的对角线相交于点 ,且 ,过 作 交 于点 ,若 的周长为 ,则平行四边形 的周长为 .
14. 在 中,,,,则 边上的中线 .
15. 如图,在边长为 的正方形 中, 是 边上的一点,且 ,点 为对角线 上的动点,则 周长的最小值为 .
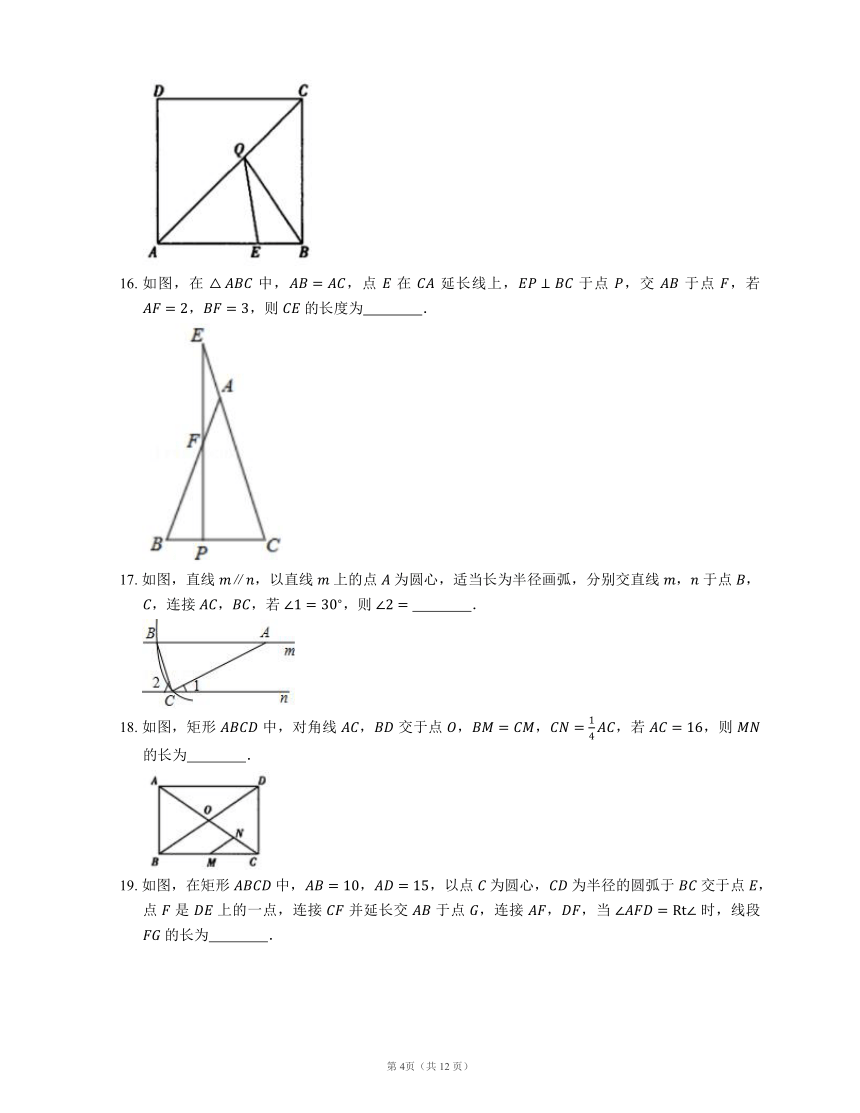
16. 如图,在 中,,点 在 延长线上, 于点 ,交 于点 ,若 ,,则 的长度为 .
17. 如图,直线 ,以直线 上的点 为圆心,适当长为半径画弧,分别交直线 , 于点 ,,连接 ,,若 ,则 .
18. 如图,矩形 中,对角线 , 交于点 ,,,若 ,则 的长为 .
19. 如图,在矩形 中,,,以点 为圆心, 为半径的圆弧于 交于点 ,点 是 上的一点,连接 并延长交 于点 ,连接 ,,当 时,线段 的长为 .
20. 如图,在由 个边长都为 且有一个锐角为 的小菱形组成的网格中,点 是其中的一个顶点,以点 为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的格点直角三角形斜边的长 .
三、解答题(共4小题;共52分)
21. 如图,在长方形 中,点 在边 上,.试说明:.
22. 如图,点 是平行四边形 边 上的中点,, 的延长线交于点 ,连接 .求证:四边形 为平行四边形.
23. 如图,点 ,,, 在同一条直线上,点 , 分别在直线 的两侧,且 ,,.
(1)求证:四边形 是平行四边形;
(2)若 ,,,则 时,四边形 是菱形.
24. 如图,,,, 是 的中点.求证:.
答案
第一部分
1. C
2. C 【解析】分三种情况:
①当直线不经过原矩形的任何一个顶点时,矩形被分割成一个五边形和一个三角形,
;
②当直线经过原矩形的一个顶点时,矩形被分割成一个四边形和一个三角形,
;
③当直线经过原矩形的两个不相邻的顶点时,矩形被分割成两个三角形,
.
故选C.
3. C
4. C 【解析】因为四边形 是菱形,
所以 , 平分 ,且 ,
所以 ,
所以 是等边三角形,
所以 .
5. C
6. C 【解析】如图,
四边形 是平行四边形,
,,
,,
平分 ,
,
,
,
,,
,
的值等于 .
7. C 【解析】 是 的中位线,
.
的长度不变,
的长也不改变.
8. C 【解析】,
,.
,.
.
,
.
.
9. B 【解析】连接 ,如图所示,
因为四边形 是矩形,
所以 ,,,,
因为 ,
所以 ,
设 ,则 ,
在 中,
由勾股定理得,,
解得 ,
即 .
故选B.
10. B
【解析】设 ,则 .
矩形纸片 中,,,现将其沿 对折,使得点 与点 重合,
.
在 中,
,
.
解得 .
第二部分
11.
【解析】平行四边形是中心对称图形,对角线的交点是对称中心,所以点 , 关于原点对称.
12.
【解析】如图,连接 .
由作图可知, 垂直平分线段 ,
,
四边形 是矩形,
,
.
13.
【解析】 四边形 是平行四边形,
是 的中点,
又 ,
,
的周长为 ,
,即 ,
平行四边形 的周长= .
14.
15.
【解析】如图,连接 交 于点 ,连接 .
四边形 是正方形,
点 与点 关于直线 对称,
,
易知 的长即为 的最小值,
,
周长的最小值为 .
16.
【解析】在 中,
,
,
,
,,
,
又 ,
,
,
是等腰三角形.
又 ,,
,,
.
17.
【解析】 直线 ,
,
,
,
.
18.
【解析】 四边形 为矩形,,
,
,
,,
为 的中位线,
,
.
19.
【解析】 四边形 是矩形,
,
,
,
,
,
,
,
,
,,
,,
,
,
,
解得:.
20. ,,
第三部分
21. 四边形 为长方形,
,.
,
,
即 .
在 和 中,
,
.
22. 在平行四边形 中,.
.
为 的中点,
,
在 和 中,
,
,
又 ,
四边形 是平行四边形.
23. (1) 因为 ,
所以 ,
在 和 中,
所以 (),
所以 ,,
所以 ,
所以四边形 是平行四边形.
(2)
【解析】若使四边形 是菱形,需 .
因为 ,,,
所以 ,
因为 ,且由四边形 是菱形知 ,
所以 为等边三角形,
所以 ,
所以当 时,四边形 是菱形,
故答案为 .
24. 如图,连接 ,.
在 和 中,
,
,
为等腰三角形.
是 的中点,
.
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 如图,点 ,, 的坐标分别为 ,, 从下面四个点 , , , 中选择一个点,以 ,, 与该点为顶点的四边形不是中心对称图形,则该点是
A. B. C. D.
2. 如图所示的矩形 ,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为 和 ,则 不可能是
A. B. C. D.
3. 若三角形的三条中位线长分别为 ,,,则原三角形的周长为
A. B. C. D.
4. 如图,四边形 是菱形,,,则 的长是
A. B. C. D.
5. 下列图形中能够用来做平面镶嵌的图形的是
A. 正八边形 B. 正七边形 C. 正六边形 D. 正五边形
6. 如图,在平行四边形 中,,, 的平分线交 与点 ,交 的延长线于点 ,则 的值等于
A. B. C. D.
7. 如图,已知矩形 ,, 分别是 , 上的点,, 分别是 , 的中点,当 在 上从 向 移动而 不动时,那么下列结论成立的是
A. 线段 的长逐渐增大 B. 线段 的长逐渐减小
C. 线段 的长不改变 D. 线段 的长不能确定
8. 如图所示,将 绕点 顺时针旋转 得 ,若点 恰好落在 上,且 的度数为 ,则 的度数为
A. B. C. D.
9. 如图,在矩形 中,,,过对角线交点 作 交 于点 ,交 于点 ,则 的长是
A. B. C. D.
10. 如图 所示,矩形纸片 中,,,现将其沿EF对折,使得点 与点 重合,则 的长为
A. B. C. D.
二、填空题(共10小题;共50分)
11. 平行四边形 的对角线的交点在坐标原点,且 ,若点 的坐标为 ,则点 的坐标为 .
12. 如图, 是矩形 的对角线,分别以点 , 为圆心,以大于 的长为半径画弧,两弧交于点 ,,直线 交 于点 ,交 于点 ,若 ,,则线段 的长为 .
13. 如图,平行四边形 的对角线相交于点 ,且 ,过 作 交 于点 ,若 的周长为 ,则平行四边形 的周长为 .
14. 在 中,,,,则 边上的中线 .
15. 如图,在边长为 的正方形 中, 是 边上的一点,且 ,点 为对角线 上的动点,则 周长的最小值为 .
16. 如图,在 中,,点 在 延长线上, 于点 ,交 于点 ,若 ,,则 的长度为 .
17. 如图,直线 ,以直线 上的点 为圆心,适当长为半径画弧,分别交直线 , 于点 ,,连接 ,,若 ,则 .
18. 如图,矩形 中,对角线 , 交于点 ,,,若 ,则 的长为 .
19. 如图,在矩形 中,,,以点 为圆心, 为半径的圆弧于 交于点 ,点 是 上的一点,连接 并延长交 于点 ,连接 ,,当 时,线段 的长为 .
20. 如图,在由 个边长都为 且有一个锐角为 的小菱形组成的网格中,点 是其中的一个顶点,以点 为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的格点直角三角形斜边的长 .
三、解答题(共4小题;共52分)
21. 如图,在长方形 中,点 在边 上,.试说明:.
22. 如图,点 是平行四边形 边 上的中点,, 的延长线交于点 ,连接 .求证:四边形 为平行四边形.
23. 如图,点 ,,, 在同一条直线上,点 , 分别在直线 的两侧,且 ,,.
(1)求证:四边形 是平行四边形;
(2)若 ,,,则 时,四边形 是菱形.
24. 如图,,,, 是 的中点.求证:.
答案
第一部分
1. C
2. C 【解析】分三种情况:
①当直线不经过原矩形的任何一个顶点时,矩形被分割成一个五边形和一个三角形,
;
②当直线经过原矩形的一个顶点时,矩形被分割成一个四边形和一个三角形,
;
③当直线经过原矩形的两个不相邻的顶点时,矩形被分割成两个三角形,
.
故选C.
3. C
4. C 【解析】因为四边形 是菱形,
所以 , 平分 ,且 ,
所以 ,
所以 是等边三角形,
所以 .
5. C
6. C 【解析】如图,
四边形 是平行四边形,
,,
,,
平分 ,
,
,
,
,,
,
的值等于 .
7. C 【解析】 是 的中位线,
.
的长度不变,
的长也不改变.
8. C 【解析】,
,.
,.
.
,
.
.
9. B 【解析】连接 ,如图所示,
因为四边形 是矩形,
所以 ,,,,
因为 ,
所以 ,
设 ,则 ,
在 中,
由勾股定理得,,
解得 ,
即 .
故选B.
10. B
【解析】设 ,则 .
矩形纸片 中,,,现将其沿 对折,使得点 与点 重合,
.
在 中,
,
.
解得 .
第二部分
11.
【解析】平行四边形是中心对称图形,对角线的交点是对称中心,所以点 , 关于原点对称.
12.
【解析】如图,连接 .
由作图可知, 垂直平分线段 ,
,
四边形 是矩形,
,
.
13.
【解析】 四边形 是平行四边形,
是 的中点,
又 ,
,
的周长为 ,
,即 ,
平行四边形 的周长= .
14.
15.
【解析】如图,连接 交 于点 ,连接 .
四边形 是正方形,
点 与点 关于直线 对称,
,
易知 的长即为 的最小值,
,
周长的最小值为 .
16.
【解析】在 中,
,
,
,
,,
,
又 ,
,
,
是等腰三角形.
又 ,,
,,
.
17.
【解析】 直线 ,
,
,
,
.
18.
【解析】 四边形 为矩形,,
,
,
,,
为 的中位线,
,
.
19.
【解析】 四边形 是矩形,
,
,
,
,
,
,
,
,
,,
,,
,
,
,
解得:.
20. ,,
第三部分
21. 四边形 为长方形,
,.
,
,
即 .
在 和 中,
,
.
22. 在平行四边形 中,.
.
为 的中点,
,
在 和 中,
,
,
又 ,
四边形 是平行四边形.
23. (1) 因为 ,
所以 ,
在 和 中,
所以 (),
所以 ,,
所以 ,
所以四边形 是平行四边形.
(2)
【解析】若使四边形 是菱形,需 .
因为 ,,,
所以 ,
因为 ,且由四边形 是菱形知 ,
所以 为等边三角形,
所以 ,
所以当 时,四边形 是菱形,
故答案为 .
24. 如图,连接 ,.
在 和 中,
,
,
为等腰三角形.
是 的中点,
.
第1页(共1 页)
同课章节目录
