2021-2022学年高一下学期数学北师大版(2019)必修第二册2.5.1向量的数量积课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册2.5.1向量的数量积课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 21:52:13 | ||
图片预览






文档简介
(共25张PPT)
§5 从力的做功到向量的数量积
5.1 向量的数量积
北师大(2019)必修2
聚焦知识目标
1.了解三角函数是研究周期现象最重要的模型.(重点)
2.初步体会如何利用三角函数研究简单的实际问题.(难点)
1.理解平面向量数量积的含义及其物理意义.
2.体会平面向量数量积与投影数量的关系.
3.会进行平面向量数量积的运算.
4.能运用数量积的运算性质和运算律解决涉及长度、夹角、平行、垂直的几何问题.
数学素养
1.通过向量数量积及投影概念的学习,培养数学抽象素养.
2.通过数量积的应用,培养数学运算素养.
课程导图
情境引入
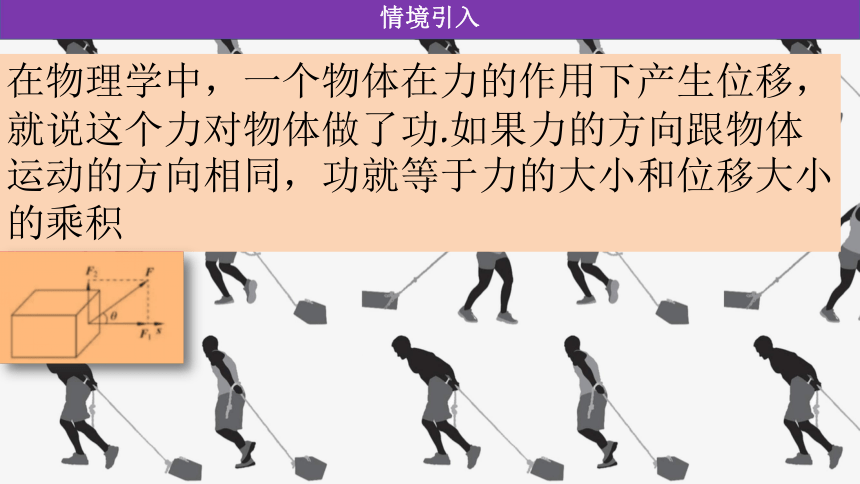
在物理学中,一个物体在力的作用下产生位移,就说这个力对物体做了功.如果力的方向跟物体运动的方向相同,功就等于力的大小和位移大小的乘积
情境引入
如果力F的方向与物体运动的方向成θ角.我们可以将力F进行分解:
与位移方向平行的分力F1满足, =cosθ.物体在F1的方向上产生了位移s,因而力F对物体做的功为|F|cos θ |s|
与位移方向垂直的分力F2,由于没有使物体在该分力的方向上产生位移,因而对物体不做功.
情境引入
综上可知,力F对物体做的功为W=|F| |s|cos θ
当0≤θ<90时,W>0,即力F做正功;当θ=90时,W=0,即力F不做功;
当90<θ≤180时,W<0,即力F做负功.
情境引入
力对物体所做的功是一个数量、它由力和位移两个向量来确定,功可以看作力F和位移s这两个向量的某种运算的结果
平面向量数量积概念
平面向量数量积概念
当0°≤<90°时,a·b>0;
当=90°时,a·b=0;
当=90°时,a·b=0;
当90°<≤180°时,a·b<0;
当 , =0°时,a·b=| || |;
=180°时, a·b=-.
课程导图
投影
如图,已知两个非零向量a和b,作=a.=b,过点A向直线OB作垂线,垂足为A',得到a在b上的投影 =称为投影向量。
|a|cos,称为投影向量γ的数量,也称为向量a在向量b方向上的投影数量,可以表示为a
投影
实例中,与位移s方向一致的分力F1的长度为|F|cosθ,即是力F在位移s方向上的投影数量.
平面向量数量积几何意义
由向量投影的定义,可以得到向量的数量积a·b的几何意义:b的长度|b|与a在b方向上的投影数量|a|cosθ的乘积(如图),或a的长度la|与b在a方向上的投影数量|b|cosθ的乘积
平面向量数量积几何意义
1.向量b在向量a上的投影数量与向量a在向量b上的投影数量相等吗?
思考
当且仅当两向量模相等时,相等.
2.当a≠0时, 由a·b=0一定能得到b=0吗?
不一定.例如,当a⊥b时,即使b≠0,也有a·b=0.
平面向量数量积
典例
例1如图,已知向量a与b,其中3,=4,且a与b的夹角θ=150°.(1)求a·b;(2)求向量b在a方向上的投影数量,并画图解释.
解(1)a·b=a|b|cosθ
(2)如图,作过点B作直线OA的垂线,垂足为B,则 所以向量b在a方向上的投影数量为
课程导图
数量积运算律
数量积运算律
例2.已知向量a、b.c.其中la|=4.|b|=6,且a与c的夹角θ=120°,b与c的夹角γ=60°,求a+b在c方向上的投影数量.
解:a+b在c方向上的投影数量为
=|a|cosθ+|b| cosγ
60°
=1
课程导图
数量积性质
≤
这些性质都可以用向量数量积的定义和几何意义来证明.
学以致用
1.已知a与b共线,且|a|=1,|b|=2.求a·b.
2.已知|a|=4,|b|=2,求分别在下列条件下a·b的值;
(1)=120°,(2)a⊥b;(3)a//b.
3.在△ABC中,=a,=b,如果a·b=0,试判断△ABC的形状
§5 从力的做功到向量的数量积
5.1 向量的数量积
北师大(2019)必修2
聚焦知识目标
1.了解三角函数是研究周期现象最重要的模型.(重点)
2.初步体会如何利用三角函数研究简单的实际问题.(难点)
1.理解平面向量数量积的含义及其物理意义.
2.体会平面向量数量积与投影数量的关系.
3.会进行平面向量数量积的运算.
4.能运用数量积的运算性质和运算律解决涉及长度、夹角、平行、垂直的几何问题.
数学素养
1.通过向量数量积及投影概念的学习,培养数学抽象素养.
2.通过数量积的应用,培养数学运算素养.
课程导图
情境引入
在物理学中,一个物体在力的作用下产生位移,就说这个力对物体做了功.如果力的方向跟物体运动的方向相同,功就等于力的大小和位移大小的乘积
情境引入
如果力F的方向与物体运动的方向成θ角.我们可以将力F进行分解:
与位移方向平行的分力F1满足, =cosθ.物体在F1的方向上产生了位移s,因而力F对物体做的功为|F|cos θ |s|
与位移方向垂直的分力F2,由于没有使物体在该分力的方向上产生位移,因而对物体不做功.
情境引入
综上可知,力F对物体做的功为W=|F| |s|cos θ
当0≤θ<90时,W>0,即力F做正功;当θ=90时,W=0,即力F不做功;
当90<θ≤180时,W<0,即力F做负功.
情境引入
力对物体所做的功是一个数量、它由力和位移两个向量来确定,功可以看作力F和位移s这两个向量的某种运算的结果
平面向量数量积概念
平面向量数量积概念
当0°≤<90°时,a·b>0;
当=90°时,a·b=0;
当=90°时,a·b=0;
当90°<≤180°时,a·b<0;
当 , =0°时,a·b=| || |;
=180°时, a·b=-.
课程导图
投影
如图,已知两个非零向量a和b,作=a.=b,过点A向直线OB作垂线,垂足为A',得到a在b上的投影 =称为投影向量。
|a|cos,称为投影向量γ的数量,也称为向量a在向量b方向上的投影数量,可以表示为a
投影
实例中,与位移s方向一致的分力F1的长度为|F|cosθ,即是力F在位移s方向上的投影数量.
平面向量数量积几何意义
由向量投影的定义,可以得到向量的数量积a·b的几何意义:b的长度|b|与a在b方向上的投影数量|a|cosθ的乘积(如图),或a的长度la|与b在a方向上的投影数量|b|cosθ的乘积
平面向量数量积几何意义
1.向量b在向量a上的投影数量与向量a在向量b上的投影数量相等吗?
思考
当且仅当两向量模相等时,相等.
2.当a≠0时, 由a·b=0一定能得到b=0吗?
不一定.例如,当a⊥b时,即使b≠0,也有a·b=0.
平面向量数量积
典例
例1如图,已知向量a与b,其中3,=4,且a与b的夹角θ=150°.(1)求a·b;(2)求向量b在a方向上的投影数量,并画图解释.
解(1)a·b=a|b|cosθ
(2)如图,作过点B作直线OA的垂线,垂足为B,则 所以向量b在a方向上的投影数量为
课程导图
数量积运算律
数量积运算律
例2.已知向量a、b.c.其中la|=4.|b|=6,且a与c的夹角θ=120°,b与c的夹角γ=60°,求a+b在c方向上的投影数量.
解:a+b在c方向上的投影数量为
=|a|cosθ+|b| cosγ
60°
=1
课程导图
数量积性质
≤
这些性质都可以用向量数量积的定义和几何意义来证明.
学以致用
1.已知a与b共线,且|a|=1,|b|=2.求a·b.
2.已知|a|=4,|b|=2,求分别在下列条件下a·b的值;
(1)=120°,(2)a⊥b;(3)a//b.
3.在△ABC中,=a,=b,如果a·b=0,试判断△ABC的形状
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
