2021-2022学年人教版七年级数学下册寒假预习5.3平行线的性质同步达标测评 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册寒假预习5.3平行线的性质同步达标测评 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 189.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 11:15:38 | ||
图片预览



文档简介
2021-2022学年人教版七年级数学下册《5-3平行线的性质》寒假预习同步测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠2=42°,则∠1=( )
A.48° B.42° C.40° D.45°
2.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.30° B.40° C.50° D.60°
3.一副直角三角板如图放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上.若DE∥CF,则∠BDF等于( )
A.35° B.30° C.25° D.15°
4.如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
A.130° B.50° C.40° D.25°
5.将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
A.105° B.115° C.95° D.110°
6.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
7.如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
A.60° B.68° C.70° D.72°
8.如图,OP∥QR∥ST,则下列各式中正确的是( )
A.∠1+∠2+∠3=180° B.∠1+∠2﹣∠3=90°
C.∠1﹣∠2+∠3=90° D.∠2+∠3﹣∠1=180°
9.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=20°,那么∠3的度数是( )
A.25° B.30° C.60° D.65°
10.已知:如图,AB∥CD∥EF,∠ABC=50°,∠CEF=150°,则∠BCE的值为( )
A.50° B.30° C.20° D.60°
二.填空题(共8小题,满分40分)
11.将一矩形纸条按如图所示折叠,若∠1=110°,则∠2= .
12.如图,已知AB∥DE,∠BAC=m°,∠CDE=n°,则∠ACD= .
13.把一张对边互相平行的纸条折成如图那样,EF是折痕,若∠EFB=32°,则∠D′FD的度数为 .
14.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为 .
15.如图,把一张长方形纸片沿AB折叠后,若∠1=48°,则∠2的大小为 度.
16.如图,l1∥l2,∠1=105°,∠2=140°,则∠α= .
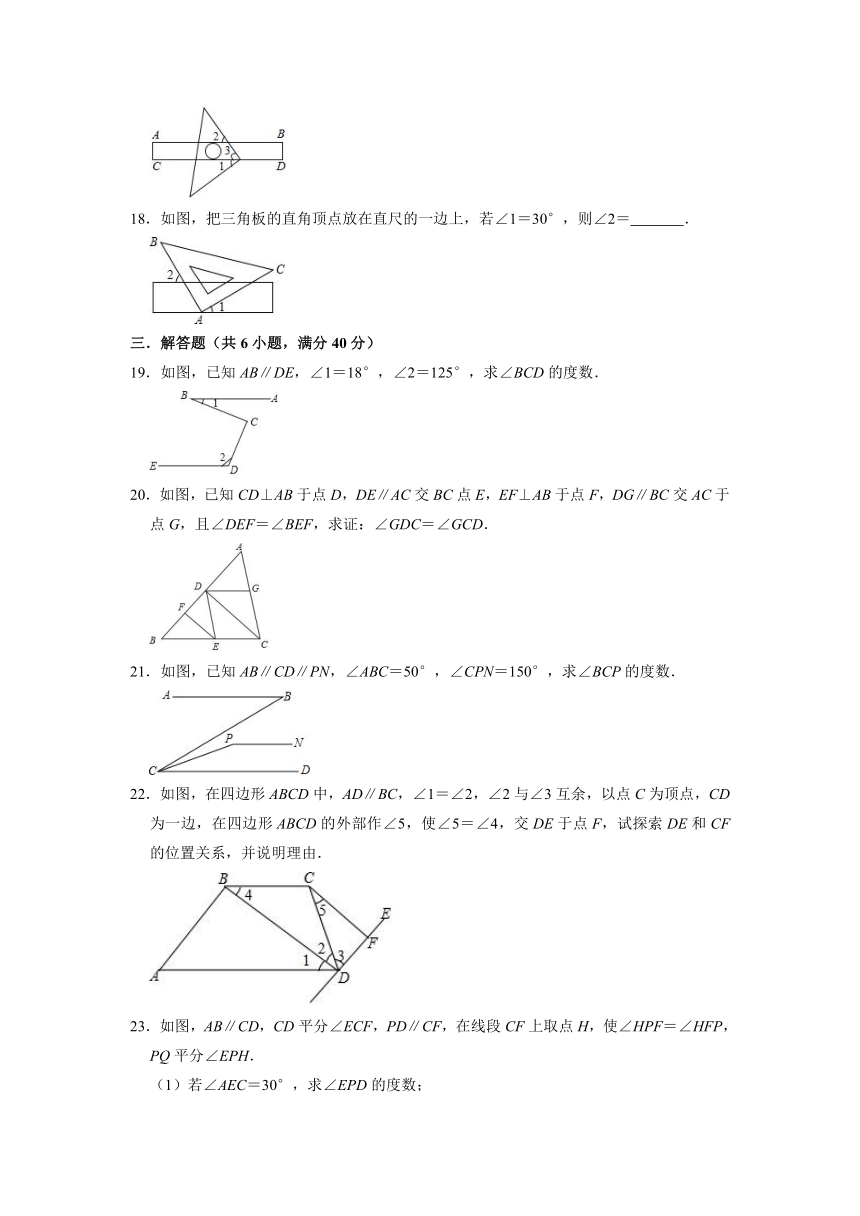
17.如图,把一块等腰直角三角板的直角顶点放在直尺的一边上,如果∠1=40°,那么∠2= °.
18.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2= .
三.解答题(共6小题,满分40分)
19.如图,已知AB∥DE,∠1=18°,∠2=125°,求∠BCD的度数.
20.如图,已知CD⊥AB于点D,DE∥AC交BC点E,EF⊥AB于点F,DG∥BC交AC于点G,且∠DEF=∠BEF,求证:∠GDC=∠GCD.
21.如图,已知AB∥CD∥PN,∠ABC=50°,∠CPN=150°,求∠BCP的度数.
22.如图,在四边形ABCD中,AD∥BC,∠1=∠2,∠2与∠3互余,以点C为顶点,CD为一边,在四边形ABCD的外部作∠5,使∠5=∠4,交DE于点F,试探索DE和CF的位置关系,并说明理由.
23.如图,AB∥CD,CD平分∠ECF,PD∥CF,在线段CF上取点H,使∠HPF=∠HFP,PQ平分∠EPH.
(1)若∠AEC=30°,求∠EPD的度数;
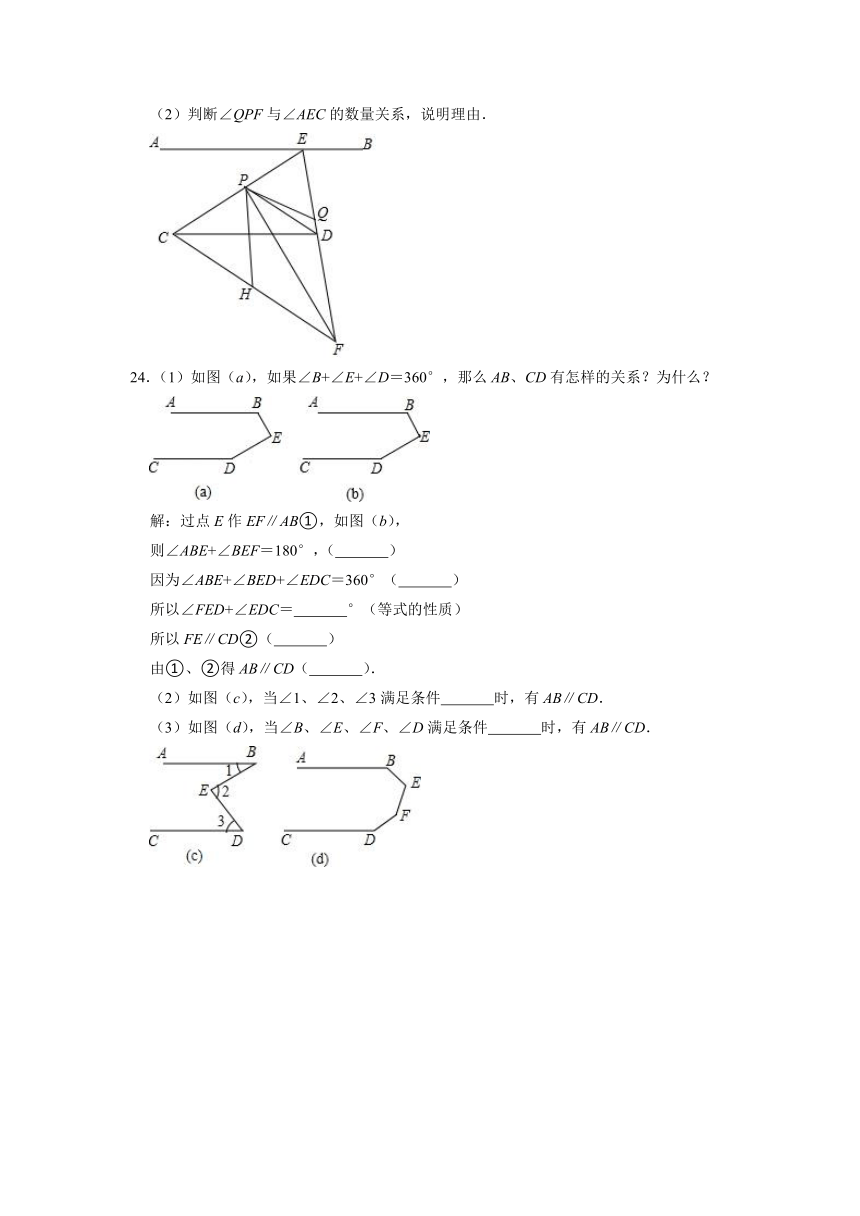
(2)判断∠QPF与∠AEC的数量关系,说明理由.
24.(1)如图(a),如果∠B+∠E+∠D=360°,那么AB、CD有怎样的关系?为什么?
解:过点E作EF∥AB①,如图(b),
则∠ABE+∠BEF=180°,( )
因为∠ABE+∠BED+∠EDC=360°( )
所以∠FED+∠EDC= °(等式的性质)
所以FE∥CD②( )
由①、②得AB∥CD( ).
(2)如图(c),当∠1、∠2、∠3满足条件 时,有AB∥CD.
(3)如图(d),当∠B、∠E、∠F、∠D满足条件 时,有AB∥CD.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,∵∠2=42°,
∴∠3=90°﹣∠2=48°,
∴∠1=48°.
故选:A.
2.解:如图,∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°,
故选:C.
3.解:由题意可得:∠EDF=30°,∠ABC=45°,
∵DE∥CB,
∴∠BDE=∠ABC=45°,
∴∠BDF=45°﹣30°=15°.
故选:D.
4.解:∵直线a∥b,
∴∠ABC=∠1=50°,
又∵AC⊥b,
∴∠2=90°﹣50°=40°,
故选:C.
5.解:∵DE∥BC,
∴∠D=∠DCB=45°,
∴∠α=∠DCB+∠B=45°+60°=105°.
故选:A.
6.解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠C=∠ACG+∠CDH=∠A+∠D﹣(180°﹣∠E),
∴∠A﹣∠C+∠D+∠E=180°.
故选:C.
7.解:∵AB∥CD,∠C=35°,
∴∠ABC=∠C=35°,
∵BC平分∠ABE,
∴∠ABE=2∠ABC=70°,
∵AB∥CD,
∴∠BED=∠ABE=70°.
故选:C.
8.解:方法一、延长TS,
∵OP∥QR∥ST,
∴∠2=∠4,
∵∠3与∠ESR互补,
∴∠ESR=180°﹣∠3,
∵∠4是△FSR的外角,
∴∠FSR+∠1=∠4,即180°﹣∠3+∠1=∠2,
∴∠2+∠3﹣∠1=180°.
方法二、∵OP∥QR∥ST,
∴∠2+∠PRQ=180°,∠3=∠1+∠PRQ,
∴∠2+∠3﹣∠1=180°,
故选:D.
9.解:∵AB∥CD,
∴∠3=∠EFD,
又∠1=20°,∠EFG=45°,
∴∠3=∠EFD=∠EFG+∠1=65°.
故选:D.
10.解:∵AB∥CD∥EF,
∴∠ABC=∠BCD=50°,∠CEF+∠ECD=180°;
∴∠ECD=180°﹣∠CEF=30°,
∴∠BCE=∠BCD﹣∠ECD=20°.
故选:C.
二.填空题(共8小题,满分40分)
11.解:∵AB∥CD,
∴∠2=∠3,∠1+∠5=180°,
∴∠5=180°﹣110°=70°,
由折叠可得,∠4=∠5=70°,
∴∠3=180°﹣70°﹣70°=40°,
∴∠2=40°,
故答案为:40°.
12.解:延长ED交AC于F,
∵AB∥DE,
∴∠3=∠BAC=m°,∠1=180°﹣∠3=180°﹣m°,
∠2=180°﹣∠CDE=180°﹣n°,
故∠C=∠3﹣∠2=m°﹣180°+n°=m°+n°﹣180°.
故答案是:m°+n°﹣180°.
13.解:∵EF 是折痕,∠EFB=32°,AC′∥BD′,
∴∠C′EF=∠GEF=32°,
∴∠C′EG=64°,
∵CE∥FD,
∴∠D′FD=∠EGB=64°.
故答案为:64°.
14.解:过点B作BD∥l,
∵直线l∥m,
∴BD∥l∥m,
∴∠4=∠1,∠2=∠3,
∴∠1+∠2=∠3+∠4=∠ABC,
∵∠ABC=45°,
∴∠1+∠2=45°.
故答案为:45°.
15.解:如图,∵∠1=48°,
∴∠DAE=132°,
由折叠可得,∠DAB=∠DAE=66°,
∵AD∥BC,
∴∠2=∠DAB=66°,
故答案为:66.
16.解:过点A作AB∥l1,
∵l1∥l2,
∴AB∥l1∥l2,
∴∠1+∠3=180°,∠2+∠4=180°,
∵∠1=105°,∠2=140°,
∴∠3=75°,∠4=40°,
∵∠α+∠3+∠4=180°,
∴∠α=65°.
故答案为:65°.
17.解:∵∠1+∠3=90°,∠1=40°,
∴∠3=50°,
∵AB∥CD,
∴∠2=∠3=50°.
故答案为50.
18.解:∵∠1=30°,
∴∠3=180°﹣90°﹣30°=60°,
∵直尺两边互相平行,
∴∠2=∠3=60°,
故答案为:60°.
三.解答题(共6小题,满分40分)
19.解:过点C作CF∥AB,如图所示:
∵AB∥DE,CF∥AB,
∴CF∥DE,
∴∠2+∠4=180°,
又∵∠2=125°,
∴∠4=55°,
又∵CF∥AB,
∴∠1=∠3,
又∵∠1=18°,
∴∠3=18°,
又∵∠BCD=∠3+∠4,
∴∠BCD=73°.
20.证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠1=∠DEF,∠2=∠BEF,
又∵∠DEF=∠BEF,
∴∠1=∠2,
∵DE∥AC,DG∥BC,
∴∠1=∠GCD,∠2=∠GDC,
∴∠GDC=∠GCD.
21.解:∵AB∥CD∥PN,
∴∠BCD=∠ABC=50°,∠DCP=180°﹣∠CPN=180°﹣150°=30°,
∴∠BCP=∠BCD﹣∠DCP=50°﹣30°=20°.
22.解:DE⊥CF,理由如下:
∵AD∥BC,∠1=∠2,
∴∠1=∠4=∠2,
又∵∠5=∠4,
∴∠5=∠2,
又∵∠2与∠3互余,
∴∠3与∠5互余,
∴∠5+∠3=90°,
∴DE⊥CF.
23.解:(1)∵AB∥CD,
∴∠DCE=∠AEC=30°,
又∵CD平分∠ECF,
∴∠ECF=2∠DCE=60°,
∵PD∥CF,
∴∠EPD=∠ECF=60°;
(2)∵∠HPF=∠HFP,∠CHP是△PHF的外角,
∴∠HPF=∠PHC,
∵PQ平分∠EPH,
∴∠QPH=∠EPH,
∴∠QPF=∠QPH﹣∠FPH
=∠EPH﹣∠PHC
=(∠EPH﹣∠PHC)
=∠ECF
=∠ECD
由AB∥CD可得,∠ECD=∠AEC,
∴∠QPF=∠AEC.
24.解:(1)
过点E作EF∥AB,如图(b),
则∠ABE+∠BEF=180°,(两直线平行,同旁内角互补)
因为∠ABE+∠BED+∠EDC=360°,(已知 )
所以∠FED+∠EDC=180°,(等式的性质)
所以 FE∥CD,(同旁内角互补,两直线平行)
∴AB∥CD (或平行线的传递性 ).
(2)如图(c),当∠1、∠2、∠3满足条件∠1+∠3=∠2时,有AB∥CD.
理由:过点E作EF∥AB.
∴∠1=∠BEF;
∵∠1+∠3=∠2,∠2=∠BEF+∠DEF,
∴∠3=∠DEF,
∴EF∥CD,
∴AB∥CD(平行线的传递性);
(3)如图(d),当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.
理由:
过点E、F分别作GE∥HF∥CD.
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠E+∠F+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB∥GE,
∴AB∥CD;
故答案是:(1)两直线平行,同旁内角互补、已知、180、同旁内角互补,两直线平行或平行线的传递性;
(2)∠1+∠3=∠2;
(3)∠B+∠E+∠F+∠D=540°.
一.选择题(共10小题,满分40分)
1.如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠2=42°,则∠1=( )
A.48° B.42° C.40° D.45°
2.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.30° B.40° C.50° D.60°
3.一副直角三角板如图放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上.若DE∥CF,则∠BDF等于( )
A.35° B.30° C.25° D.15°
4.如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
A.130° B.50° C.40° D.25°
5.将一副直角三角板按如图方式放置,使直角顶点C重合,当DE∥BC时,∠α的度数是( )
A.105° B.115° C.95° D.110°
6.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
7.如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠BED的度数是( )
A.60° B.68° C.70° D.72°
8.如图,OP∥QR∥ST,则下列各式中正确的是( )
A.∠1+∠2+∠3=180° B.∠1+∠2﹣∠3=90°
C.∠1﹣∠2+∠3=90° D.∠2+∠3﹣∠1=180°
9.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=20°,那么∠3的度数是( )
A.25° B.30° C.60° D.65°
10.已知:如图,AB∥CD∥EF,∠ABC=50°,∠CEF=150°,则∠BCE的值为( )
A.50° B.30° C.20° D.60°
二.填空题(共8小题,满分40分)
11.将一矩形纸条按如图所示折叠,若∠1=110°,则∠2= .
12.如图,已知AB∥DE,∠BAC=m°,∠CDE=n°,则∠ACD= .
13.把一张对边互相平行的纸条折成如图那样,EF是折痕,若∠EFB=32°,则∠D′FD的度数为 .
14.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为 .
15.如图,把一张长方形纸片沿AB折叠后,若∠1=48°,则∠2的大小为 度.
16.如图,l1∥l2,∠1=105°,∠2=140°,则∠α= .
17.如图,把一块等腰直角三角板的直角顶点放在直尺的一边上,如果∠1=40°,那么∠2= °.
18.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2= .
三.解答题(共6小题,满分40分)
19.如图,已知AB∥DE,∠1=18°,∠2=125°,求∠BCD的度数.
20.如图,已知CD⊥AB于点D,DE∥AC交BC点E,EF⊥AB于点F,DG∥BC交AC于点G,且∠DEF=∠BEF,求证:∠GDC=∠GCD.
21.如图,已知AB∥CD∥PN,∠ABC=50°,∠CPN=150°,求∠BCP的度数.
22.如图,在四边形ABCD中,AD∥BC,∠1=∠2,∠2与∠3互余,以点C为顶点,CD为一边,在四边形ABCD的外部作∠5,使∠5=∠4,交DE于点F,试探索DE和CF的位置关系,并说明理由.
23.如图,AB∥CD,CD平分∠ECF,PD∥CF,在线段CF上取点H,使∠HPF=∠HFP,PQ平分∠EPH.
(1)若∠AEC=30°,求∠EPD的度数;
(2)判断∠QPF与∠AEC的数量关系,说明理由.
24.(1)如图(a),如果∠B+∠E+∠D=360°,那么AB、CD有怎样的关系?为什么?
解:过点E作EF∥AB①,如图(b),
则∠ABE+∠BEF=180°,( )
因为∠ABE+∠BED+∠EDC=360°( )
所以∠FED+∠EDC= °(等式的性质)
所以FE∥CD②( )
由①、②得AB∥CD( ).
(2)如图(c),当∠1、∠2、∠3满足条件 时,有AB∥CD.
(3)如图(d),当∠B、∠E、∠F、∠D满足条件 时,有AB∥CD.
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,∵∠2=42°,
∴∠3=90°﹣∠2=48°,
∴∠1=48°.
故选:A.
2.解:如图,∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°,
故选:C.
3.解:由题意可得:∠EDF=30°,∠ABC=45°,
∵DE∥CB,
∴∠BDE=∠ABC=45°,
∴∠BDF=45°﹣30°=15°.
故选:D.
4.解:∵直线a∥b,
∴∠ABC=∠1=50°,
又∵AC⊥b,
∴∠2=90°﹣50°=40°,
故选:C.
5.解:∵DE∥BC,
∴∠D=∠DCB=45°,
∴∠α=∠DCB+∠B=45°+60°=105°.
故选:A.
6.解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠C=∠ACG+∠CDH=∠A+∠D﹣(180°﹣∠E),
∴∠A﹣∠C+∠D+∠E=180°.
故选:C.
7.解:∵AB∥CD,∠C=35°,
∴∠ABC=∠C=35°,
∵BC平分∠ABE,
∴∠ABE=2∠ABC=70°,
∵AB∥CD,
∴∠BED=∠ABE=70°.
故选:C.
8.解:方法一、延长TS,
∵OP∥QR∥ST,
∴∠2=∠4,
∵∠3与∠ESR互补,
∴∠ESR=180°﹣∠3,
∵∠4是△FSR的外角,
∴∠FSR+∠1=∠4,即180°﹣∠3+∠1=∠2,
∴∠2+∠3﹣∠1=180°.
方法二、∵OP∥QR∥ST,
∴∠2+∠PRQ=180°,∠3=∠1+∠PRQ,
∴∠2+∠3﹣∠1=180°,
故选:D.
9.解:∵AB∥CD,
∴∠3=∠EFD,
又∠1=20°,∠EFG=45°,
∴∠3=∠EFD=∠EFG+∠1=65°.
故选:D.
10.解:∵AB∥CD∥EF,
∴∠ABC=∠BCD=50°,∠CEF+∠ECD=180°;
∴∠ECD=180°﹣∠CEF=30°,
∴∠BCE=∠BCD﹣∠ECD=20°.
故选:C.
二.填空题(共8小题,满分40分)
11.解:∵AB∥CD,
∴∠2=∠3,∠1+∠5=180°,
∴∠5=180°﹣110°=70°,
由折叠可得,∠4=∠5=70°,
∴∠3=180°﹣70°﹣70°=40°,
∴∠2=40°,
故答案为:40°.
12.解:延长ED交AC于F,
∵AB∥DE,
∴∠3=∠BAC=m°,∠1=180°﹣∠3=180°﹣m°,
∠2=180°﹣∠CDE=180°﹣n°,
故∠C=∠3﹣∠2=m°﹣180°+n°=m°+n°﹣180°.
故答案是:m°+n°﹣180°.
13.解:∵EF 是折痕,∠EFB=32°,AC′∥BD′,
∴∠C′EF=∠GEF=32°,
∴∠C′EG=64°,
∵CE∥FD,
∴∠D′FD=∠EGB=64°.
故答案为:64°.
14.解:过点B作BD∥l,
∵直线l∥m,
∴BD∥l∥m,
∴∠4=∠1,∠2=∠3,
∴∠1+∠2=∠3+∠4=∠ABC,
∵∠ABC=45°,
∴∠1+∠2=45°.
故答案为:45°.
15.解:如图,∵∠1=48°,
∴∠DAE=132°,
由折叠可得,∠DAB=∠DAE=66°,
∵AD∥BC,
∴∠2=∠DAB=66°,
故答案为:66.
16.解:过点A作AB∥l1,
∵l1∥l2,
∴AB∥l1∥l2,
∴∠1+∠3=180°,∠2+∠4=180°,
∵∠1=105°,∠2=140°,
∴∠3=75°,∠4=40°,
∵∠α+∠3+∠4=180°,
∴∠α=65°.
故答案为:65°.
17.解:∵∠1+∠3=90°,∠1=40°,
∴∠3=50°,
∵AB∥CD,
∴∠2=∠3=50°.
故答案为50.
18.解:∵∠1=30°,
∴∠3=180°﹣90°﹣30°=60°,
∵直尺两边互相平行,
∴∠2=∠3=60°,
故答案为:60°.
三.解答题(共6小题,满分40分)
19.解:过点C作CF∥AB,如图所示:
∵AB∥DE,CF∥AB,
∴CF∥DE,
∴∠2+∠4=180°,
又∵∠2=125°,
∴∠4=55°,
又∵CF∥AB,
∴∠1=∠3,
又∵∠1=18°,
∴∠3=18°,
又∵∠BCD=∠3+∠4,
∴∠BCD=73°.
20.证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠1=∠DEF,∠2=∠BEF,
又∵∠DEF=∠BEF,
∴∠1=∠2,
∵DE∥AC,DG∥BC,
∴∠1=∠GCD,∠2=∠GDC,
∴∠GDC=∠GCD.
21.解:∵AB∥CD∥PN,
∴∠BCD=∠ABC=50°,∠DCP=180°﹣∠CPN=180°﹣150°=30°,
∴∠BCP=∠BCD﹣∠DCP=50°﹣30°=20°.
22.解:DE⊥CF,理由如下:
∵AD∥BC,∠1=∠2,
∴∠1=∠4=∠2,
又∵∠5=∠4,
∴∠5=∠2,
又∵∠2与∠3互余,
∴∠3与∠5互余,
∴∠5+∠3=90°,
∴DE⊥CF.
23.解:(1)∵AB∥CD,
∴∠DCE=∠AEC=30°,
又∵CD平分∠ECF,
∴∠ECF=2∠DCE=60°,
∵PD∥CF,
∴∠EPD=∠ECF=60°;
(2)∵∠HPF=∠HFP,∠CHP是△PHF的外角,
∴∠HPF=∠PHC,
∵PQ平分∠EPH,
∴∠QPH=∠EPH,
∴∠QPF=∠QPH﹣∠FPH
=∠EPH﹣∠PHC
=(∠EPH﹣∠PHC)
=∠ECF
=∠ECD
由AB∥CD可得,∠ECD=∠AEC,
∴∠QPF=∠AEC.
24.解:(1)
过点E作EF∥AB,如图(b),
则∠ABE+∠BEF=180°,(两直线平行,同旁内角互补)
因为∠ABE+∠BED+∠EDC=360°,(已知 )
所以∠FED+∠EDC=180°,(等式的性质)
所以 FE∥CD,(同旁内角互补,两直线平行)
∴AB∥CD (或平行线的传递性 ).
(2)如图(c),当∠1、∠2、∠3满足条件∠1+∠3=∠2时,有AB∥CD.
理由:过点E作EF∥AB.
∴∠1=∠BEF;
∵∠1+∠3=∠2,∠2=∠BEF+∠DEF,
∴∠3=∠DEF,
∴EF∥CD,
∴AB∥CD(平行线的传递性);
(3)如图(d),当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.
理由:
过点E、F分别作GE∥HF∥CD.
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠E+∠F+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB∥GE,
∴AB∥CD;
故答案是:(1)两直线平行,同旁内角互补、已知、180、同旁内角互补,两直线平行或平行线的传递性;
(2)∠1+∠3=∠2;
(3)∠B+∠E+∠F+∠D=540°.
