2021-2022学年人教版九年级数学下册第二十七章 相似 单元测试训练卷(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十七章 相似 单元测试训练卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 13:47:39 | ||
图片预览


文档简介
人教版九年级数学下册
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如果两个相似多边形面积的比为1∶5,则它们的相似比为( )
A.1∶25 B.1∶5 C.1∶2.5 D.1∶
2. 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=( )
A. B. C. D.1
3. 如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到CD,则C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
4. 已知△ABC∽△DEF,相似比为3:1,且△ABC的面积与△DEF的面积和为20,则△DEF的面积为( )
A.5 B.2 C.15 D.18
5. 如图,在平行四边形ABCD中, EF∥AB交AD于点E,交DB于点F,DE?EA=3?4,EF=3,则CD的长为( )
A.4 B.7 C.3 D.12
6. 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
A.18 B. C. D.
7. 如图,图中共有相似三角形( )
A.2对 B.3对 C.4对 D.5对
8. 如图,在等腰三角形ABC中,AB=AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC的面积为42,则四边形DBCE的面积是( )
A.20 B.22 C.24 D.26
9.如图,铁路道口的栏杆短臂长1 m,长臂长16 m.当短臂端点下降0.5 m时,长臂端点升高(杆的宽度忽略不计)( )
A.4 m B.6 m C.8 m D.12 m
10. 如图,在锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC,得矩形MPQN.设MN的长为x,矩形MPQN的面积为y,则y关于x的函数图象大致形状是( )
二.填空题(共6小题,4*6=24)
11. 如图,要使△ABC与△DBA相似,则只需添加一个适当的条件___________________.(填一个即可)
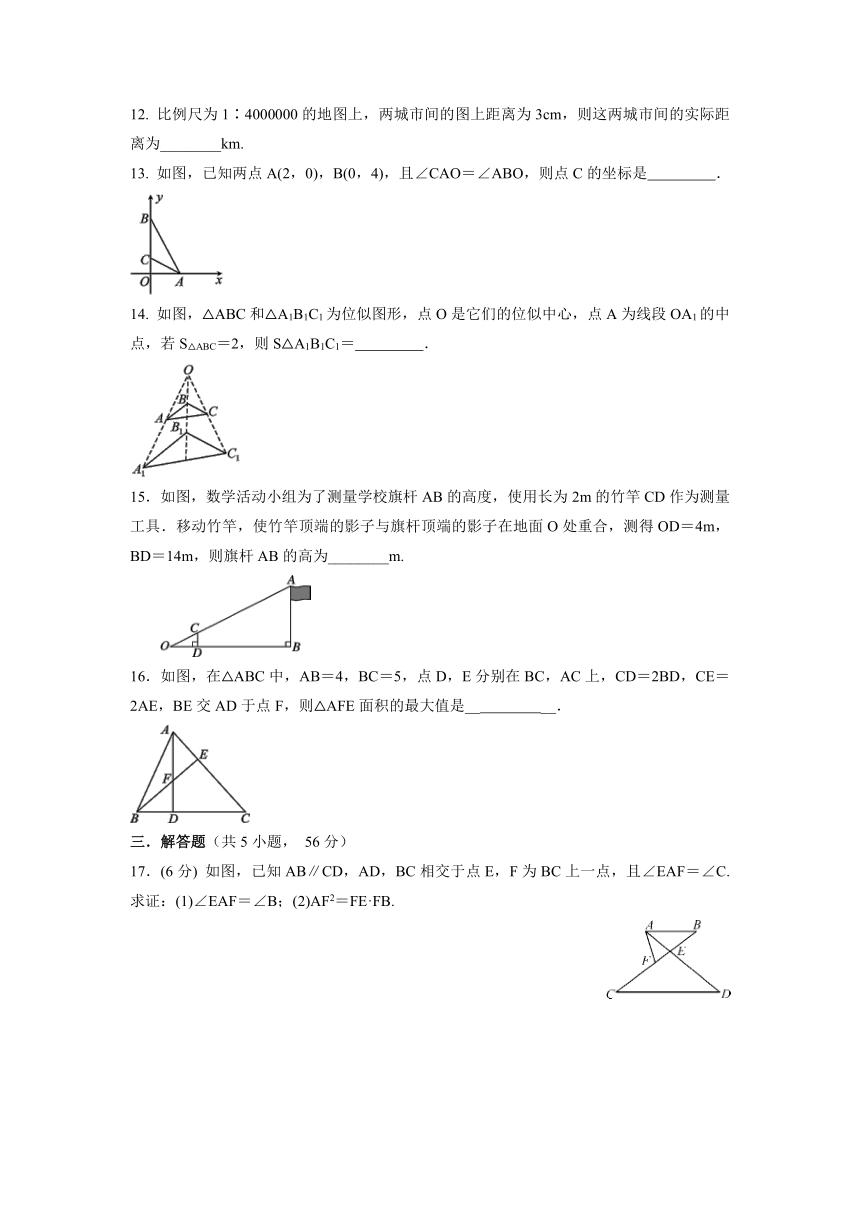
12. 比例尺为1∶4000000的地图上,两城市间的图上距离为3cm,则这两城市间的实际距离为________km.
13. 如图,已知两点A(2,0),B(0,4),且∠CAO=∠ABO,则点C的坐标是 .
14. 如图,△ABC和△A1B1C1为位似图形,点O是它们的位似中心,点A为线段OA1的中点,若S△ABC=2,则S△A1B1C1= .
15.如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m,BD=14m,则旗杆AB的高为________m.
16.如图,在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是__ __.
三.解答题(共5小题, 56分)
17.(6分) 如图,已知AB∥CD,AD,BC相交于点E,F为BC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE·FB.
18.(8分) 如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°.
(1)求证△ABE∽△ECD;
(2)若AB=4,BE=,求CD的长.
19.(8分) 一天晚上,李明和张龙利用灯光下的影子来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立身高AM与其影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m.已知李明直立时的身高为1.75m,求路灯CD的高.
20.(10分) 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
21.(12分) 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
22.(12分) 如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点,=,求的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证:··=1;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若=,=,求的值.
参考答案
1-5DBABB 6-10BCDCB
11.∠C=∠BAD或∠BAC=∠BDA(答案不唯一)
12.120
13.(0,1)
14.8
15.9
16.
17.解:(1)∵AB∥CD,∴∠B=∠C,又∠C=∠EAF,∴∠EAF=∠B
(2)∵∠EAF=∠B,∠AFE=∠BFA,∴△AFE∽△BFA,则=,∴AF2=FE·FB
18.(1)证明:在Rt△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.∵∠AEC=∠B+∠BAE=∠AED+∠CED,∠AED=45°,∴∠BAE=∠CED.∴△ABE∽△ECD.
(2)解:在Rt△ABC中,∠BAC=90°,AB=AC=4,∴BC=4.∵BE=,∴EC=3.∵△ABE∽△ECD,∴=,即=,解得CD=.
19.解:设CD=xm.∵AE=AM,AM⊥EC,∴∠E=45°,∴EC=CD=xm,AC=(x-1.75)m.∵CD⊥EC,BN⊥EC,BN∥CD,∴△ABN∽△ACD,∴=,即=,解得x=6.125.答:路灯CD的高为6.125m.
20.(1)证明:∵△ABC和△CEF均为等腰直角三角形,∴==,∠ACB=∠ECF=45°.∵∠ACB=∠ACE+∠BCE,∠ECF=∠BCF+∠BCE,∴∠ACE=∠BCF,∴△CAE∽△CBF.
(2)解:由(1)可知△CAE∽△CBF,∴∠CAE=∠CBF,==.又∵AE=2,∴=,∴BF=.∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴EF2=BE2+BF2=12+()2=3,∴EF=,∴CE=EF=.
21.(1)证明:如图,连接OD,
∵OB=OD,∴∠OBD=∠BDO.∵∠CDA=∠CBD,∴∠CDA=∠ODB.又∵AB是⊙O的直径,∴∠ADB=90°,∴∠ADO+∠ODB=90°,∴∠ADO+∠CDA=90°,即∠CDO=90°,∴OD⊥CD,∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)∵∠C=∠C,∠CDA=∠CBD,∴△CDA∽△CBD,∴=.∵=,BC=6,∴CD=4.∵CE,BE都是⊙O的切线,∴BE=DE,BE⊥BC,∴BE2+BC2=EC2,即BE2+62=(4+BE)2.解得BE=.
22.(1)解:过点A作MN的平行线交BN的延长线于点G.∵ON∥AG,∴=.∵O是AC的中点,∴AO=CO,∴NG=CN.∵MN∥AG,∴=,∴===.
(2)证明:由(1)可知=,=,∴··=··=1.
(3)解:在△ABD中,点P是AD上一点,过点P的直线与AB,BD的延长线分别相交于点F,C.由(2)可得··=1.在△ACD中,过点P的直线与AC,CD的延长线分别相交于点E,B.由(2)可得··=1.∴··=··,∴=·=×=.
第二十七章 相似
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 如果两个相似多边形面积的比为1∶5,则它们的相似比为( )
A.1∶25 B.1∶5 C.1∶2.5 D.1∶
2. 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=( )
A. B. C. D.1
3. 如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到CD,则C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
4. 已知△ABC∽△DEF,相似比为3:1,且△ABC的面积与△DEF的面积和为20,则△DEF的面积为( )
A.5 B.2 C.15 D.18
5. 如图,在平行四边形ABCD中, EF∥AB交AD于点E,交DB于点F,DE?EA=3?4,EF=3,则CD的长为( )
A.4 B.7 C.3 D.12
6. 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
A.18 B. C. D.
7. 如图,图中共有相似三角形( )
A.2对 B.3对 C.4对 D.5对
8. 如图,在等腰三角形ABC中,AB=AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC的面积为42,则四边形DBCE的面积是( )
A.20 B.22 C.24 D.26
9.如图,铁路道口的栏杆短臂长1 m,长臂长16 m.当短臂端点下降0.5 m时,长臂端点升高(杆的宽度忽略不计)( )
A.4 m B.6 m C.8 m D.12 m
10. 如图,在锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC,得矩形MPQN.设MN的长为x,矩形MPQN的面积为y,则y关于x的函数图象大致形状是( )
二.填空题(共6小题,4*6=24)
11. 如图,要使△ABC与△DBA相似,则只需添加一个适当的条件___________________.(填一个即可)
12. 比例尺为1∶4000000的地图上,两城市间的图上距离为3cm,则这两城市间的实际距离为________km.
13. 如图,已知两点A(2,0),B(0,4),且∠CAO=∠ABO,则点C的坐标是 .
14. 如图,△ABC和△A1B1C1为位似图形,点O是它们的位似中心,点A为线段OA1的中点,若S△ABC=2,则S△A1B1C1= .
15.如图,数学活动小组为了测量学校旗杆AB的高度,使用长为2m的竹竿CD作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O处重合,测得OD=4m,BD=14m,则旗杆AB的高为________m.
16.如图,在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE=2AE,BE交AD于点F,则△AFE面积的最大值是__ __.
三.解答题(共5小题, 56分)
17.(6分) 如图,已知AB∥CD,AD,BC相交于点E,F为BC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE·FB.
18.(8分) 如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°.
(1)求证△ABE∽△ECD;
(2)若AB=4,BE=,求CD的长.
19.(8分) 一天晚上,李明和张龙利用灯光下的影子来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立身高AM与其影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m.已知李明直立时的身高为1.75m,求路灯CD的高.
20.(10分) 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
21.(12分) 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
22.(12分) 如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点,=,求的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证:··=1;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若=,=,求的值.
参考答案
1-5DBABB 6-10BCDCB
11.∠C=∠BAD或∠BAC=∠BDA(答案不唯一)
12.120
13.(0,1)
14.8
15.9
16.
17.解:(1)∵AB∥CD,∴∠B=∠C,又∠C=∠EAF,∴∠EAF=∠B
(2)∵∠EAF=∠B,∠AFE=∠BFA,∴△AFE∽△BFA,则=,∴AF2=FE·FB
18.(1)证明:在Rt△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.∵∠AEC=∠B+∠BAE=∠AED+∠CED,∠AED=45°,∴∠BAE=∠CED.∴△ABE∽△ECD.
(2)解:在Rt△ABC中,∠BAC=90°,AB=AC=4,∴BC=4.∵BE=,∴EC=3.∵△ABE∽△ECD,∴=,即=,解得CD=.
19.解:设CD=xm.∵AE=AM,AM⊥EC,∴∠E=45°,∴EC=CD=xm,AC=(x-1.75)m.∵CD⊥EC,BN⊥EC,BN∥CD,∴△ABN∽△ACD,∴=,即=,解得x=6.125.答:路灯CD的高为6.125m.
20.(1)证明:∵△ABC和△CEF均为等腰直角三角形,∴==,∠ACB=∠ECF=45°.∵∠ACB=∠ACE+∠BCE,∠ECF=∠BCF+∠BCE,∴∠ACE=∠BCF,∴△CAE∽△CBF.
(2)解:由(1)可知△CAE∽△CBF,∴∠CAE=∠CBF,==.又∵AE=2,∴=,∴BF=.∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴EF2=BE2+BF2=12+()2=3,∴EF=,∴CE=EF=.
21.(1)证明:如图,连接OD,
∵OB=OD,∴∠OBD=∠BDO.∵∠CDA=∠CBD,∴∠CDA=∠ODB.又∵AB是⊙O的直径,∴∠ADB=90°,∴∠ADO+∠ODB=90°,∴∠ADO+∠CDA=90°,即∠CDO=90°,∴OD⊥CD,∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)∵∠C=∠C,∠CDA=∠CBD,∴△CDA∽△CBD,∴=.∵=,BC=6,∴CD=4.∵CE,BE都是⊙O的切线,∴BE=DE,BE⊥BC,∴BE2+BC2=EC2,即BE2+62=(4+BE)2.解得BE=.
22.(1)解:过点A作MN的平行线交BN的延长线于点G.∵ON∥AG,∴=.∵O是AC的中点,∴AO=CO,∴NG=CN.∵MN∥AG,∴=,∴===.
(2)证明:由(1)可知=,=,∴··=··=1.
(3)解:在△ABD中,点P是AD上一点,过点P的直线与AB,BD的延长线分别相交于点F,C.由(2)可得··=1.在△ACD中,过点P的直线与AC,CD的延长线分别相交于点E,B.由(2)可得··=1.∴··=··,∴=·=×=.
