2021-2022学年人教版八年级数学上册11.3多边形及其内角和 提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.3多边形及其内角和 提升训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 125.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 10:33:11 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《11-3多边形及其内角和》自主提升训练(附答案)
1.一个多边形的每一个外角都等于30°,则这个多边形是( )
A.九边形 B.十边形 C.十一边形 D.十二边形
2.下列图形中具有稳定性的是( )
A.平行四边形 B.长方形 C.正方形 D.三角形
3.如图,点F在正五边形ABCDE的边CD的延长线上,连接BD,则∠BDF的度数( )
A.36° B.144° C.134° D.120°
4.一个多边形的内角和是它的外角和的2倍,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
5.内角和等于外角和的多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
6.如图,△ABC中∠A=115°,若图中沿虚线剪去∠A,则∠1+∠2等于( )
A.180° B.230° C.290° D.295°
7.某多边形内角和与外角和共1080°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
8.在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则下列结论一定正确的是( )
A.∠ADE=20° B.∠ADE=∠ADC
C.∠ADE=30° D.∠ADE=∠ADC
9.一个多边形截去一角后,变成一个八边形则这个多边形原来的边数是( )
A.8或9 B.7或8 C.7或8或9 D.8或9或10
10.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于 .
11.若一个多边形每个外角都等于与它相邻的内角的一半,则这个多边形的内角和为 度.
12.若多边形的每个内角都相等,每个内角与相邻外角的差为100°,则这个多边形的边数为 .
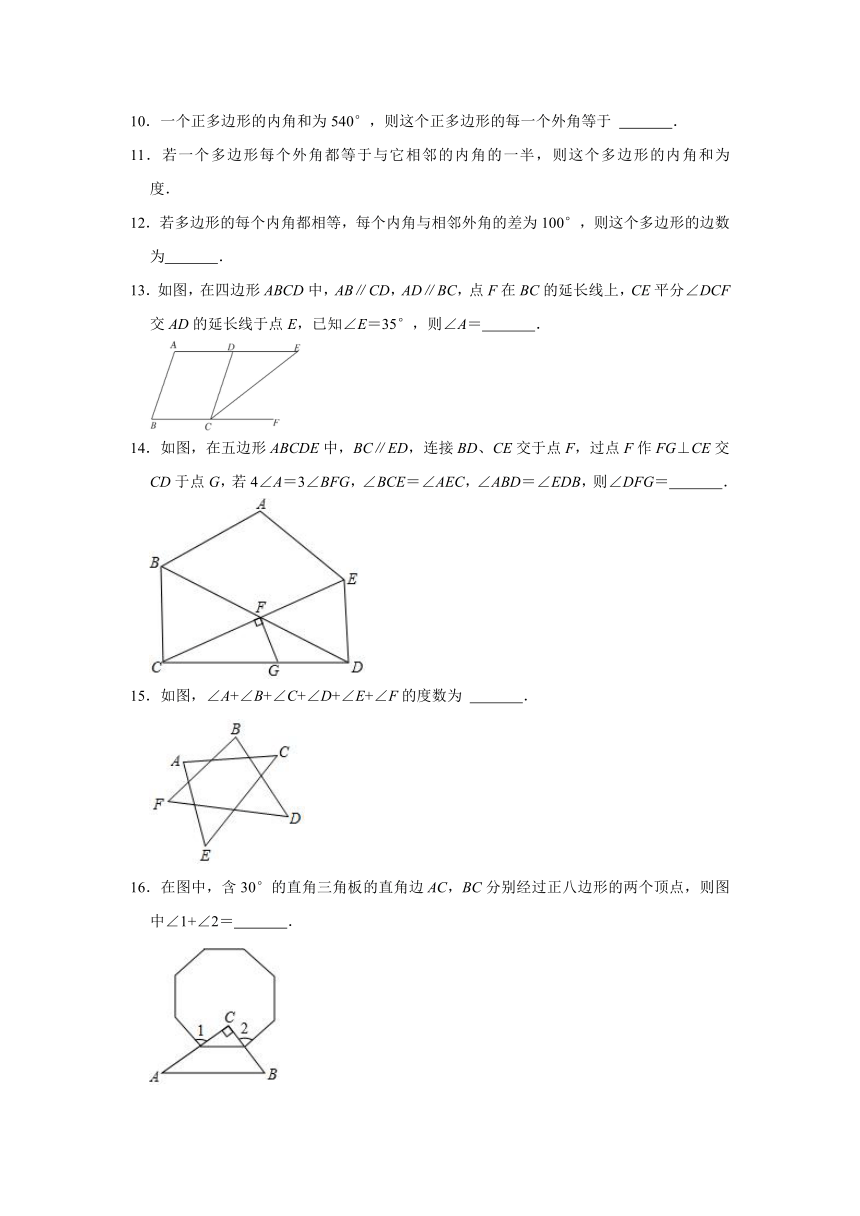
13.如图,在四边形ABCD中,AB∥CD,AD∥BC,点F在BC的延长线上,CE平分∠DCF交AD的延长线于点E,已知∠E=35°,则∠A= .
14.如图,在五边形ABCDE中,BC∥ED,连接BD、CE交于点F,过点F作FG⊥CE交CD于点G,若4∠A=3∠BFG,∠BCE=∠AEC,∠ABD=∠EDB,则∠DFG= .
15.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为 .
16.在图中,含30°的直角三角板的直角边AC,BC分别经过正八边形的两个顶点,则图中∠1+∠2= .
17.如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,CE交AD于点F,若∠EAD和∠ECD的角平分线相交于点P.
(1)求证:AB∥CD;
(2)若∠E=60°,∠B=80°,求∠APC的度数.
18.如图,在四边形ABCD中,BD⊥CD,EF⊥CD,且∠1=∠2.
(1)求证:AD∥BC;
(2)若BD平分∠ABC,∠A=130°,求∠C的度数.
19.如图,把△ABC纸片沿DE折叠,
(1)如图一,当点A落在四边形BCED内部时,∠A=50°,则∠1+∠2= .
(2)根据图一,写出∠A和∠1+∠2之间的数量关系规律: ;
(3)如图二,当点A落在四边形BCED外部时,∠A与∠1+∠2之间有一种数量关系是 ,并加以证明.
20.【问题背景】小明在学习多边形时,把如图1的图形成为“8”字形,并得出如下结论:∠A+∠B=∠C+∠D,请你说明理由;
(2)【尝试应用】如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的
度数;
小明结合(1)中的结论并利用方程思想轻松解答如下:
解:由AP、CP分别平分∠BAD、∠BCD,可设∠1=∠2=x,∠3=∠4=y,
由(1)的结论得:,①+②,
得2∠P+x+y=x+y+∠B+∠D
∴(∠B+∠D)=26°
(3)【拓展延伸】如图3,已知∠C=α,∠B=β,∠CAP=∠CAB,∠CDP=∠CDB,请利用上述结论或方
法求∠P的度数.
参考答案
1.解:因为多边形的外角和是360°,
又因为多边形的每个外角都是30°,
所以这个多边形的边数为:360÷30=12.
故选:D.
2.解:长方形,正方形,三角形,平行四边形中只有三角形具有稳定性.
故选:D.
3.解:∵五边形ABCDE是正五边形,
∴∠C==108°,BC=DC,
∴∠BDC=∠DBC=(180°﹣∠C)=(180°﹣108°)=36°,
∴∠BDF=180°﹣∠BDC=180°﹣36°=144°,
故选:B.
4.解:设这个多边形是n边形,根据题意,得
(n﹣2)×180°=2×360,
解得:n=6.
故这个多边形是六边形.
故选:B.
5.解:设所求n边形边数为n,
则360°=(n﹣2) 180°,
解得n=4.
∴外角和等于内角和的多边形是四边形.
故选:B.
6.解:∵∠A=115°,
∴∠B+∠C=65°,
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣65°=295°.
故选:D.
7.解:∵多边形内角和与外角和共1080°,
∴多边形内角和=1080°﹣360°=720°,
设多边形的边数是n,
∴(n﹣2)×180°=720°,
解得n=6.
故选:A.
8.解:如图,
在△AED中,∠AED=60°,
∴∠A=180°﹣∠AED﹣∠ADE=120°﹣∠ADE,
在四边形DEBC中,∠DEB=180°﹣∠AED=180°﹣60°=120°,
∴∠B=∠C=(360°﹣∠DEB﹣∠EDC)÷2=120°﹣∠EDC,
∵∠A=∠B=∠C,
∴120°﹣∠ADE=120°﹣∠EDC,
∴∠ADE=∠EDC,
∵∠ADC=∠ADE+∠EDC=∠EDC+∠EDC=∠EDC,
∴∠ADE=∠ADC,
故选:D.
9.解:∵截去一个角后边数可以增加1,不变,减少1,
∴原多边形的边数是7或8或9.
故选:C.
10.解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5,
∴这个正多边形的每一个外角等于:=72°.
故答案为:72°.
11.解:设多边形的每一个内角为x,则每一个外角为 x,
由题意得,x+x=180°,
解得,x=120°,x=60°,
这个多边形的边数为:=6,
多边形内角和=(6﹣2)×180°=720°,
故答案为:720.
12.解:设内角是x°,外角是y°,
则得到一个方程组,
解得.
而任何多边形的外角和是360°,
则多边形外角的个数是360÷40=9,
则这个多边形的边数是九边形.
故答案为:9
13.解:∵AD∥BC,∠E=35°,
∴∠ECF=∠E=35°,
∵CE平分∠DCF,
∴∠DCE=∠ECF=35°,
∴∠CDE=180°﹣35°﹣35°=110°,
∵AB∥CD,
∴∠A=∠CDE=110°.
14.解:∵FG⊥CE,
∴∠GFC=90°,
∵4∠A=3∠BFG,
∴∠A:∠BFG=3:4,
∴设∠A=3x,∠BFG=4x,
∵BC∥ED,
∴∠EDB=∠DBC,∠DEF=∠BCE,
∵∠ABD=∠EDB,∠BCE=∠AEC,
∴∠ABD=∠EDB=∠DBC,∠BCE=∠AEC=∠DEF,
设∠ABD=∠EDB=∠DBC=a,∠BCE=∠AEC=∠DEF=b,
在四边形ABFE中,∠A=360°﹣∠ABD﹣∠BFE﹣∠ACE,即3x=360°﹣a﹣b﹣(180°﹣∠BFC),
∴3x=180°﹣a﹣b+∠BFC①,
∵∠BFG=∠BFC+∠CFG,即4x=(180°﹣a﹣b)+90°,
∴4x=270°﹣a﹣b②,
∴②﹣①得:x=90°﹣∠BFC③,
∵4x=90°+∠BFC④,
∴③+④得:5x=180°,
∴x=36°,
∴∠DFG=180°﹣∠BFG=180°﹣4x=180°﹣4×36°=36°,
故答案为:36°.
15.解:在△ACE和△BDF中,
∠A+∠C+∠E=180°,∠B+∠D+∠F=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F=180°+180°=360°,
故答案为:360°.
16.解:如图,
(8﹣2)×180°÷8×2
=6×180°÷8×2
=270°,
∠3+∠4=180°﹣90°=90°,
∠1+∠2=270°﹣90°=180°.
故答案为:180°.
17.解:(1)∵AD∥BC,
∴∠B=∠EAD,
∵∠B=∠D,
∴∠EAD=∠D,
∴AB∥CD;
(2)过点P作PG∥AB,交BC于点G,
∵AD∥BC,
∴∠EAD=∠B=80°,
∵AP平分∠EAD,
∴,
由(1)知AB∥CD,
∴∠ECD=∠E=60°,
∵CP平分∠ECD,
∴,
∵PG∥AB,AB∥CD,
∴PG∥CD,
∴∠APG=∠EAP,∠CPG=∠PCD,
∴∠APC=∠APG+∠CPG=∠EAP+∠DCP=40°+30°=70°.
18.解:(1)证明:如图,
∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(垂直于同一直线的两条直线平行),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2,
∴∠1=∠3(等量代换).
∴AD∥BC(内错角相等,两直线平行).
(2)∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵DB平分∠ABC(已知),
∴∠3=∠ABC=25°.
∴∠C=90°﹣∠3=65°.
19.解:(1)根据翻折的性质,∠A'DE=(180 ∠1),∠A'ED=(180 ∠2),
∵∠A+∠A'DE+∠A'ED=180°,∠A=50°,
∴50°+(180 ∠1)+(180 ∠2)=180°,
解得:∠1+∠2=100°,
故答案为100°;
(2)根据翻折的性质,∠A'DE=(180 ∠1),∠A'ED=(180 ∠2),
∵∠A+∠A'DE+∠A'ED=180°,
∴∠A+(180 ∠1)+(180 ∠2)=180°,
整理得:2∠A=∠1+∠2,
故答案为2∠A=∠1+∠2;
(3)2∠A=∠1﹣∠2.
证明:根据翻折的性质,∠A'DE=(180 ∠1),∠A'ED=(180+∠2),
∵∠A+∠A'DE+∠A'ED=180°,
∴∠A+(180 ∠1)+(180+∠2)=180°,
整理得:2∠A=∠1﹣∠2,
故答案为2∠A=∠1﹣∠2.
20.解:(1)证明:【问题背景】在△AOB中,∠A+∠B+∠AOB=180°,在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)【尝试应用】)∵AP、CP分别平分∠BAD.∠BCD
∴∠1=∠2,∠3=∠4,
由(1)的结论得:,
①+②,得2∠P+∠1+∠3=∠2+∠4+∠B+∠D,
∴∠P=(∠B+∠D)=26°.
(3)由(1)可得2∠P+∠CDP+∠PAB=∠C+∠B+∠CAP+∠PDB,
∵,,
∴,,
=,
∴,
由(1)可知,,
∴,
∴∠P=α+β.
1.一个多边形的每一个外角都等于30°,则这个多边形是( )
A.九边形 B.十边形 C.十一边形 D.十二边形
2.下列图形中具有稳定性的是( )
A.平行四边形 B.长方形 C.正方形 D.三角形
3.如图,点F在正五边形ABCDE的边CD的延长线上,连接BD,则∠BDF的度数( )
A.36° B.144° C.134° D.120°
4.一个多边形的内角和是它的外角和的2倍,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
5.内角和等于外角和的多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
6.如图,△ABC中∠A=115°,若图中沿虚线剪去∠A,则∠1+∠2等于( )
A.180° B.230° C.290° D.295°
7.某多边形内角和与外角和共1080°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
8.在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则下列结论一定正确的是( )
A.∠ADE=20° B.∠ADE=∠ADC
C.∠ADE=30° D.∠ADE=∠ADC
9.一个多边形截去一角后,变成一个八边形则这个多边形原来的边数是( )
A.8或9 B.7或8 C.7或8或9 D.8或9或10
10.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于 .
11.若一个多边形每个外角都等于与它相邻的内角的一半,则这个多边形的内角和为 度.
12.若多边形的每个内角都相等,每个内角与相邻外角的差为100°,则这个多边形的边数为 .
13.如图,在四边形ABCD中,AB∥CD,AD∥BC,点F在BC的延长线上,CE平分∠DCF交AD的延长线于点E,已知∠E=35°,则∠A= .
14.如图,在五边形ABCDE中,BC∥ED,连接BD、CE交于点F,过点F作FG⊥CE交CD于点G,若4∠A=3∠BFG,∠BCE=∠AEC,∠ABD=∠EDB,则∠DFG= .
15.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为 .
16.在图中,含30°的直角三角板的直角边AC,BC分别经过正八边形的两个顶点,则图中∠1+∠2= .
17.如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,CE交AD于点F,若∠EAD和∠ECD的角平分线相交于点P.
(1)求证:AB∥CD;
(2)若∠E=60°,∠B=80°,求∠APC的度数.
18.如图,在四边形ABCD中,BD⊥CD,EF⊥CD,且∠1=∠2.
(1)求证:AD∥BC;
(2)若BD平分∠ABC,∠A=130°,求∠C的度数.
19.如图,把△ABC纸片沿DE折叠,
(1)如图一,当点A落在四边形BCED内部时,∠A=50°,则∠1+∠2= .
(2)根据图一,写出∠A和∠1+∠2之间的数量关系规律: ;
(3)如图二,当点A落在四边形BCED外部时,∠A与∠1+∠2之间有一种数量关系是 ,并加以证明.
20.【问题背景】小明在学习多边形时,把如图1的图形成为“8”字形,并得出如下结论:∠A+∠B=∠C+∠D,请你说明理由;
(2)【尝试应用】如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的
度数;
小明结合(1)中的结论并利用方程思想轻松解答如下:
解:由AP、CP分别平分∠BAD、∠BCD,可设∠1=∠2=x,∠3=∠4=y,
由(1)的结论得:,①+②,
得2∠P+x+y=x+y+∠B+∠D
∴(∠B+∠D)=26°
(3)【拓展延伸】如图3,已知∠C=α,∠B=β,∠CAP=∠CAB,∠CDP=∠CDB,请利用上述结论或方
法求∠P的度数.
参考答案
1.解:因为多边形的外角和是360°,
又因为多边形的每个外角都是30°,
所以这个多边形的边数为:360÷30=12.
故选:D.
2.解:长方形,正方形,三角形,平行四边形中只有三角形具有稳定性.
故选:D.
3.解:∵五边形ABCDE是正五边形,
∴∠C==108°,BC=DC,
∴∠BDC=∠DBC=(180°﹣∠C)=(180°﹣108°)=36°,
∴∠BDF=180°﹣∠BDC=180°﹣36°=144°,
故选:B.
4.解:设这个多边形是n边形,根据题意,得
(n﹣2)×180°=2×360,
解得:n=6.
故这个多边形是六边形.
故选:B.
5.解:设所求n边形边数为n,
则360°=(n﹣2) 180°,
解得n=4.
∴外角和等于内角和的多边形是四边形.
故选:B.
6.解:∵∠A=115°,
∴∠B+∠C=65°,
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣65°=295°.
故选:D.
7.解:∵多边形内角和与外角和共1080°,
∴多边形内角和=1080°﹣360°=720°,
设多边形的边数是n,
∴(n﹣2)×180°=720°,
解得n=6.
故选:A.
8.解:如图,
在△AED中,∠AED=60°,
∴∠A=180°﹣∠AED﹣∠ADE=120°﹣∠ADE,
在四边形DEBC中,∠DEB=180°﹣∠AED=180°﹣60°=120°,
∴∠B=∠C=(360°﹣∠DEB﹣∠EDC)÷2=120°﹣∠EDC,
∵∠A=∠B=∠C,
∴120°﹣∠ADE=120°﹣∠EDC,
∴∠ADE=∠EDC,
∵∠ADC=∠ADE+∠EDC=∠EDC+∠EDC=∠EDC,
∴∠ADE=∠ADC,
故选:D.
9.解:∵截去一个角后边数可以增加1,不变,减少1,
∴原多边形的边数是7或8或9.
故选:C.
10.解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5,
∴这个正多边形的每一个外角等于:=72°.
故答案为:72°.
11.解:设多边形的每一个内角为x,则每一个外角为 x,
由题意得,x+x=180°,
解得,x=120°,x=60°,
这个多边形的边数为:=6,
多边形内角和=(6﹣2)×180°=720°,
故答案为:720.
12.解:设内角是x°,外角是y°,
则得到一个方程组,
解得.
而任何多边形的外角和是360°,
则多边形外角的个数是360÷40=9,
则这个多边形的边数是九边形.
故答案为:9
13.解:∵AD∥BC,∠E=35°,
∴∠ECF=∠E=35°,
∵CE平分∠DCF,
∴∠DCE=∠ECF=35°,
∴∠CDE=180°﹣35°﹣35°=110°,
∵AB∥CD,
∴∠A=∠CDE=110°.
14.解:∵FG⊥CE,
∴∠GFC=90°,
∵4∠A=3∠BFG,
∴∠A:∠BFG=3:4,
∴设∠A=3x,∠BFG=4x,
∵BC∥ED,
∴∠EDB=∠DBC,∠DEF=∠BCE,
∵∠ABD=∠EDB,∠BCE=∠AEC,
∴∠ABD=∠EDB=∠DBC,∠BCE=∠AEC=∠DEF,
设∠ABD=∠EDB=∠DBC=a,∠BCE=∠AEC=∠DEF=b,
在四边形ABFE中,∠A=360°﹣∠ABD﹣∠BFE﹣∠ACE,即3x=360°﹣a﹣b﹣(180°﹣∠BFC),
∴3x=180°﹣a﹣b+∠BFC①,
∵∠BFG=∠BFC+∠CFG,即4x=(180°﹣a﹣b)+90°,
∴4x=270°﹣a﹣b②,
∴②﹣①得:x=90°﹣∠BFC③,
∵4x=90°+∠BFC④,
∴③+④得:5x=180°,
∴x=36°,
∴∠DFG=180°﹣∠BFG=180°﹣4x=180°﹣4×36°=36°,
故答案为:36°.
15.解:在△ACE和△BDF中,
∠A+∠C+∠E=180°,∠B+∠D+∠F=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F=180°+180°=360°,
故答案为:360°.
16.解:如图,
(8﹣2)×180°÷8×2
=6×180°÷8×2
=270°,
∠3+∠4=180°﹣90°=90°,
∠1+∠2=270°﹣90°=180°.
故答案为:180°.
17.解:(1)∵AD∥BC,
∴∠B=∠EAD,
∵∠B=∠D,
∴∠EAD=∠D,
∴AB∥CD;
(2)过点P作PG∥AB,交BC于点G,
∵AD∥BC,
∴∠EAD=∠B=80°,
∵AP平分∠EAD,
∴,
由(1)知AB∥CD,
∴∠ECD=∠E=60°,
∵CP平分∠ECD,
∴,
∵PG∥AB,AB∥CD,
∴PG∥CD,
∴∠APG=∠EAP,∠CPG=∠PCD,
∴∠APC=∠APG+∠CPG=∠EAP+∠DCP=40°+30°=70°.
18.解:(1)证明:如图,
∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(垂直于同一直线的两条直线平行),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2,
∴∠1=∠3(等量代换).
∴AD∥BC(内错角相等,两直线平行).
(2)∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵DB平分∠ABC(已知),
∴∠3=∠ABC=25°.
∴∠C=90°﹣∠3=65°.
19.解:(1)根据翻折的性质,∠A'DE=(180 ∠1),∠A'ED=(180 ∠2),
∵∠A+∠A'DE+∠A'ED=180°,∠A=50°,
∴50°+(180 ∠1)+(180 ∠2)=180°,
解得:∠1+∠2=100°,
故答案为100°;
(2)根据翻折的性质,∠A'DE=(180 ∠1),∠A'ED=(180 ∠2),
∵∠A+∠A'DE+∠A'ED=180°,
∴∠A+(180 ∠1)+(180 ∠2)=180°,
整理得:2∠A=∠1+∠2,
故答案为2∠A=∠1+∠2;
(3)2∠A=∠1﹣∠2.
证明:根据翻折的性质,∠A'DE=(180 ∠1),∠A'ED=(180+∠2),
∵∠A+∠A'DE+∠A'ED=180°,
∴∠A+(180 ∠1)+(180+∠2)=180°,
整理得:2∠A=∠1﹣∠2,
故答案为2∠A=∠1﹣∠2.
20.解:(1)证明:【问题背景】在△AOB中,∠A+∠B+∠AOB=180°,在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)【尝试应用】)∵AP、CP分别平分∠BAD.∠BCD
∴∠1=∠2,∠3=∠4,
由(1)的结论得:,
①+②,得2∠P+∠1+∠3=∠2+∠4+∠B+∠D,
∴∠P=(∠B+∠D)=26°.
(3)由(1)可得2∠P+∠CDP+∠PAB=∠C+∠B+∠CAP+∠PDB,
∵,,
∴,,
=,
∴,
由(1)可知,,
∴,
∴∠P=α+β.
