2021-2022学年鲁教版(五四制)八年级数学下册 6.3正方形的性质与判定 同步自主达标测试(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册 6.3正方形的性质与判定 同步自主达标测试(word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 212.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 21:54:11 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》
同步自主达标测试(附答案)
一.选择题(共9小题,满分36分)
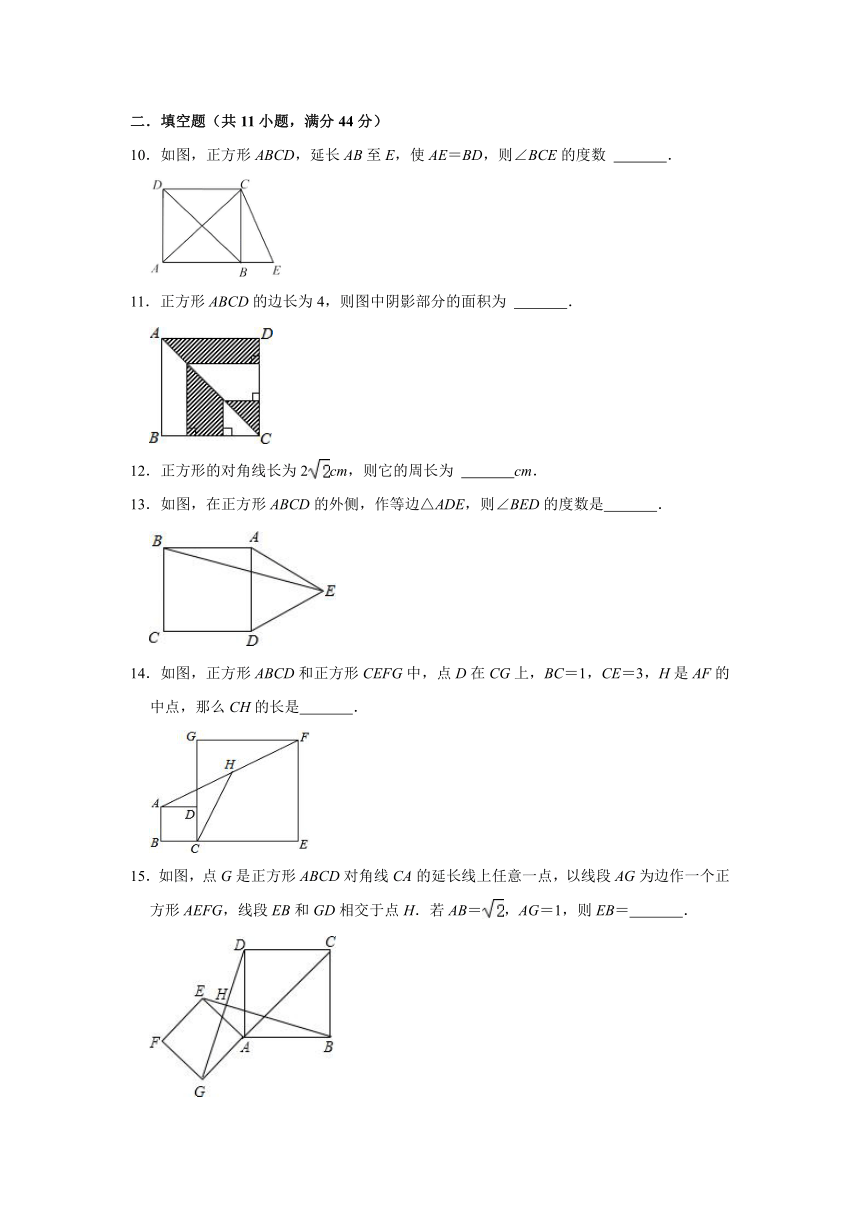
1.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
2.将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心(对角线的交点),则图中四块阴影面积的和为( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
3.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2021B2021C2021D2021的边长是( )
A.()2020 B.()2021 C.()2021 D.()2020
4.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A.75° B.60° C.54° D.67.5°
5.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
6.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选②③ C.选①③ D.选②④
7.顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
8.下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
9.如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:
①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
A.①②③ B.②③④ C.①③④ D.①②③④
二.填空题(共11小题,满分44分)
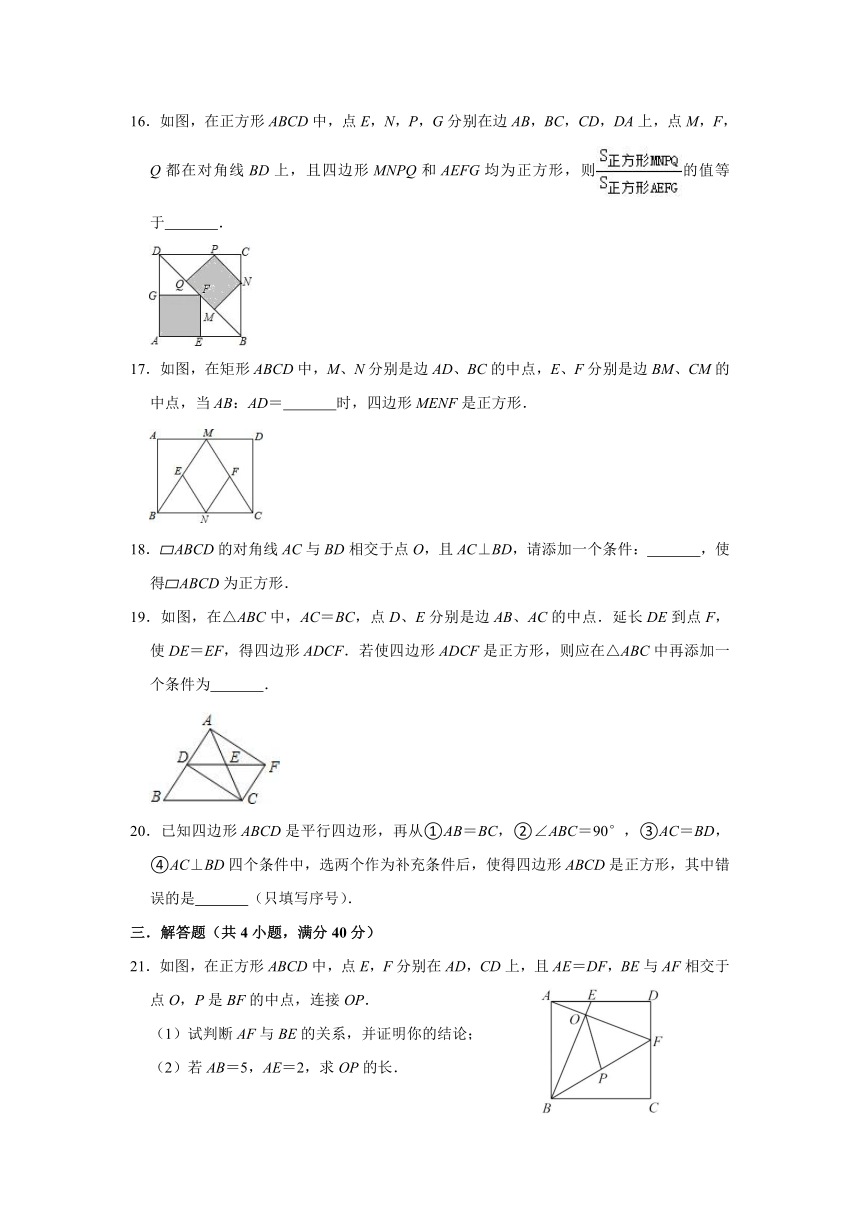
10.如图,正方形ABCD,延长AB至E,使AE=BD,则∠BCE的度数 .
11.正方形ABCD的边长为4,则图中阴影部分的面积为 .
12.正方形的对角线长为2cm,则它的周长为 cm.
13.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 .
14.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
15.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
16.如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于 .
17.如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD= 时,四边形MENF是正方形.
18. ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得 ABCD为正方形.
19.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为 .
20.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是 (只填写序号).
三.解答题(共4小题,满分40分)
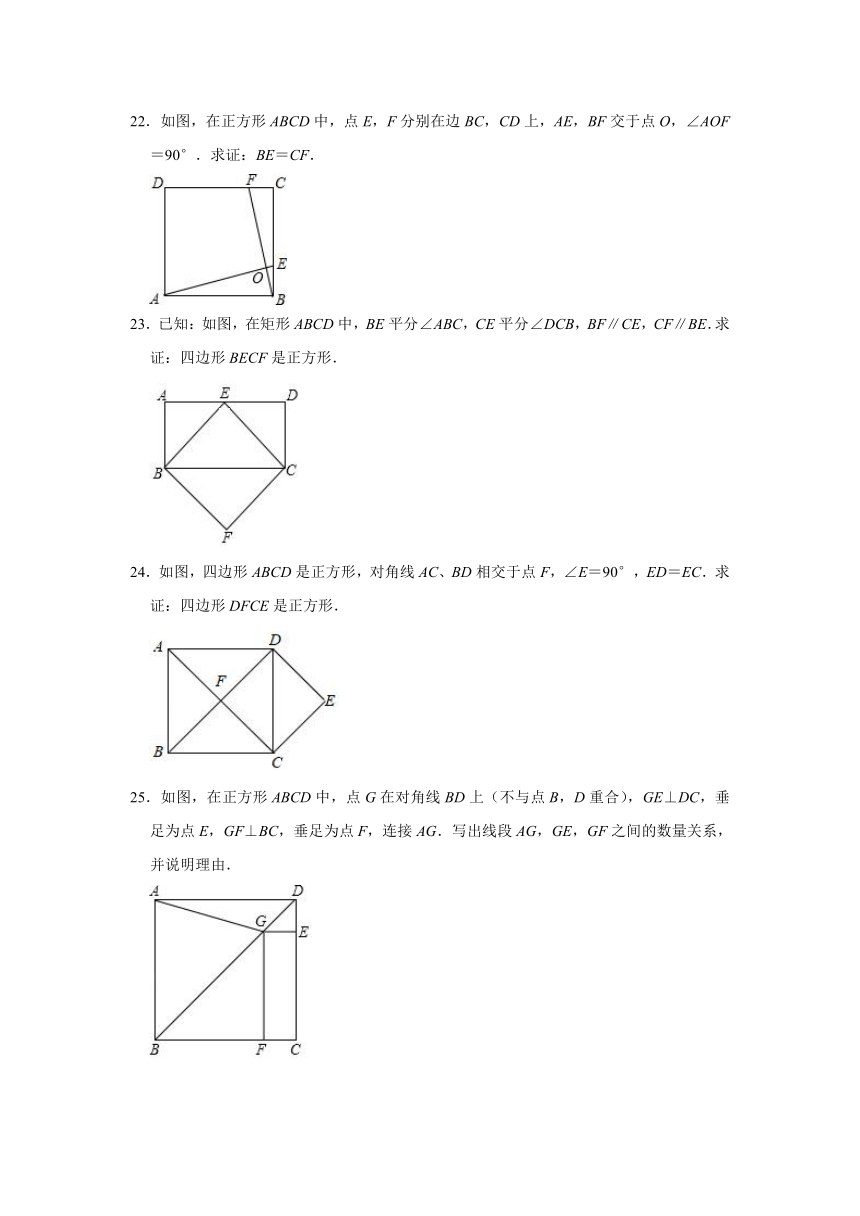
21.如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,BE与AF相交于点O,P是BF的中点,连接OP.
(1)试判断AF与BE的关系,并证明你的结论;
(2)若AB=5,AE=2,求OP的长.
22.如图,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.
23.已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
24.如图,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,ED=EC.求证:四边形DFCE是正方形.
25.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC,垂足为点E,GF⊥BC,垂足为点F,连接AG.写出线段AG,GE,GF之间的数量关系,并说明理由.
26.已知,如图,在正方形ABCD中,E为对角线AC上一点,EG⊥ED交BC于点G,EF⊥BC,垂足为F.
(1)求证:BF=GF;
(2)如图,若DE=DH,AB=8.
①求证:CG=FG;
②求EH的值.
参考答案
一.选择题(共9小题,满分40分)
1.解:∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
故选:C.
2.解:如图,连接AP,AN,点A是正方形的对角线的交点.
则AP=AN,∠APF=∠ANE=45°,
∵∠PAF+∠FAN=∠FAN+∠NAE=90°,
∴∠PAF=∠NAE,
∴△PAF≌△NAE,
∴四边形AENF的面积等于△NAP的面积,
而△NAP的面积是正方形的面积的,而正方形的面积为4,
∴四边形AENF的面积为1cm2,四块阴影面积的和为4cm2.
故选:B.
3.解:如图所示:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=,则B2C2=()1,
同理可得:B3C3==()2,
故正方形AnBn nDn的边长是:()n﹣1.
则正方形A2021B2021C2021D2021的边长是:()2020.
故选:D.
4.解:如图,连接BD,
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,BC=EC,
∴∠EBC=∠BEC=(180°﹣∠BCE)=15°
∵∠BCM=∠BCD=45°,
∴∠BMC=180°﹣(∠BCM+∠EBC)=120°,
∴∠AMB=180°﹣∠BMC=60°
∵AC是线段BD的垂直平分线,M在AC上,
∴∠AMD=∠AMB=60°
故选:B.
5.解:A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;
B、对角线互相垂直的平行四边形是菱形;故本选项错误;
C、对角线互相平分的四边形是平行四边形;故本选项正确;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误;
故选:C.
6.解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意;
C、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意.
故选:B.
7.解:如图,∵点E,F,G,H分别是四边形ABCD各边的中点,且四边形EFGH是正方形,
∴EF=EH,EF⊥EH,
∵BD=2EF,AC=2EH,
∴AC=BD,AC⊥BD,
即四边形ABCD满足对角线相等且垂直,
选项D满足题意.
故选:D.
8.解:A、一组对边平行另一组对边相等的四边形可以是等腰梯形,可以是平行四边形,故选项A不合题意;
B、对角线互相垂直平分的四边形是菱形,故选项B符合题意;
C、对角线相等的平行四边形是矩形,故选项C不合题意;
D、对角线互相垂直平分且相等的四边形是正方形,故选项D不合题意;
故选:B.
9.解:如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,
∴①不正确;
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,
∴③正确;
在△AEO和△AFO中,
,
∴△AE0≌△AF0(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,
∴②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,
∴④正确.
综上,可得正确的是:②③④.
故选:B.
二.填空题(共11小题,满分44分)
10.解:∵四边形ABCD是正方形,
∴∠BAC=∠ACB=45°,
∵AE=AC,
∴∠ACE=∠E=(180°﹣45°)=67.5°,
∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°.
故答案为:22.5°.
11.解:由图形可得:
S阴影= S正方形ABCD=×4×4=8.
故答案为:8.
12.解:如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠B=90°,
∴AB2+BC2=AC2,
∴2AB2=(2)2,
∴AB=2cm,
∴正方形ABCD的周长=4×2=8(cm);
故答案为:8.
13.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∵等边三角形ADE,
∴AD=AE,∠DAE=∠AED=60°.
∠BAE=∠BAD+∠DAE=90°+60°=150°,
AB=AE,
∠AEB=∠ABE=(180°﹣∠BAE)÷2=15°,
∠BED=∠DEA﹣∠AEB=60°﹣15°=45°.
故答案为:45°.
14.解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===2,
∴CH=,
故答案为:.
15.解:连接BD交AC于O,
∵四边形ABCD、AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG,
∴∠EAB=∠GAD,
在△AEB和△AGD中,
,
∴△EAB≌△GAD(SAS),
∴EB=GD,
∵四边形ABCD是正方形,AB=,
∴BD⊥AC,AC=BD=AB=2,
∴∠DOG=90°,OA=OD=BD=1,
∵AG=1,
∴OG=OA+AG=2,
∴GD==,
∴EB=.故答案为:.
16.解:在正方形ABCD中,
∵∠ABD=∠CBD=45°,
∵四边形MNPQ和AEFG均为正方形,
∴∠BEF=∠AEF=90°,∠BMN=∠QMN=90°,
∴△BEF与△BMN是等腰直角三角形,
∴FE=BE=AE=AB,BM=MN=QM,
同理DQ=MQ,
∴MN=BD=AB,
∴==,
故答案为:.
17.解:当AB:AD=1:2时,四边形MENF是正方形,
理由是:∵AB:AD=1:2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,
∴BM=CM,
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形,
即当AB:AD=1:2时,四边形MENF是正方形,
故答案为:1:2.
18.解:∵ ABCD的对角线AC与BD相交于点O,且AC⊥BD,
∴ ABCD是菱形,
当∠BAD=90°时, ABCD为正方形.
故答案为:∠BAD=90°.
19.解:∠ACB=90°时,四边形ADCF是正方形,
理由:∵E是AC中点,
∴AE=EC,
∵DE=EF,
∴四边形ADCF是平行四边形,
∵AD=DB,AE=EC,
∴DE=BC,
∴DF=BC,
∵CA=CB,
∴AC=DF,
∴四边形ADCF是矩形,
点D、E分别是边AB、AC的中点,
∴DE∥BC,
∵∠ACB=90°,
∴∠AED=90°,
∴矩形ADCF是正方形.
故答案为:∠ACB=90°.
20.解:有6种选法:(1)①②:由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(2)②③:由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误;
(3)①③:由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(4)②④:由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
(5)①④:由①得有一组邻边相等的平行四边形是菱形,由④得对角线互相垂直的平行四边形是菱形,所以不能得出平行四边形ABCD是正方形,错误;
(6)③④:由③得对角线相等的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
综上所述:错误的是:②③或①④;
故答案为:②③或①④.
三.解答题(共4小题,满分40分)
21.解:(1)AF=BE,理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ADC=90°,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴AF=BE;
(2)由(1)知∴△BAE≌△ADF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AOE=∠BOF=90°,
∵点P为BF的中点,
∴OP=BF,
∵BC=AB=CD=5,AE=DF=2,
∴CF=CD﹣DF=5﹣2=3,
∴BF===,
∴OP=.
22.证明:∵四边形ABCD是正方形,
∴AB=BC,
∠ABE=∠BCF=90°,
∵∠AOF=90°,∠AOB=90°,
∴∠BAE+∠OBA=90°,
又∵∠FBC+∠OBA=90°,
∴∠BAE=∠CBF(同角的余角相等),
在△ABE和△BCF中
∴,
∴△ABE≌△BCF(ASA).
∴BE=CF.
23.证明:∵BF∥CE,CF∥BE
∴四边形BECF是平行四边形,
又∵在矩形ABCD中,BE平分∠ABC,CE平分∠DCB
∴∠EBC=∠ECB=45°
∴∠BEC=90°,BE=CE
∴四边形BECF是正方形.
24.解:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
25.解:AG2=GE2+GF2,理由如下:
如图,连接CG,
∵四边形ABCD是正方形,
∴AB=BC,∠ABG=∠CBG,∠BCD=90°,
在△ABG和△CBG中,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,
∵GE⊥DC,垂足为点E,GF⊥BC,垂足为点F,
∴∠GEC=∠GFC=90°,
∴∠GEC=∠GFC=∠BCD=90°,
∴四边形CEGF是矩形,
∴GF=CE,
在Rt△CEG中,GC2=GE2+EC2,
∴AG2=GE2+GF2.
26.(1)证明:如图所示,连接EB,
∵四边形ABCD为正方形,
∴∠ACB=∠DCE,BC=CD.
又∵EC=EC,
∴△EBC≌△EDC(SAS),
∴EB=ED.
延长FE交AD于N,
∵∠NAE=45°,EF⊥BC,
∴∠NEA=45°,即AN=NE,
∵AB=AD,AD∥BC,即AB=NF,
∴ND=EF,
∵EG⊥ED,
∴∠FEG+∠EGF=∠FEG+∠NED,
∴∠EGF=∠NED,
∵∠EFG=∠END,
∴△EFG≌△DNE(AAS),
∴ED=EG,
∴EB=EG.
∵EF⊥BC,
∴BF=GF;
(2)①证明:如图所示,作GM⊥AC,垂足为M.
∵DE=DH,∠DEG=90°,
∴∠EDH=45°,
∴∠DEH=67.5°,
∴∠GEH=22.5°.
又∵∠FEC=45°,
∴∠FEG=22.5°,
∴∠FEG=∠GEM.
∵GF⊥EF,GM⊥EC,
∴GF=GM.
∵∠MCG=45°,
∴GC=GM=FG;
②解:∵AD∥BC,
由①可知,CG:FG:BF=:1:1,
∴.
即,
∴=,
∵BC=8,
∴AC=8,
∴CH=8﹣8,
∴AE=8﹣8,
∴EH=8﹣2×(8﹣8)=16﹣8.
同步自主达标测试(附答案)
一.选择题(共9小题,满分36分)
1.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
2.将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心(对角线的交点),则图中四块阴影面积的和为( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
3.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2021B2021C2021D2021的边长是( )
A.()2020 B.()2021 C.()2021 D.()2020
4.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A.75° B.60° C.54° D.67.5°
5.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
6.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选②③ C.选①③ D.选②④
7.顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
8.下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
9.如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:
①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
A.①②③ B.②③④ C.①③④ D.①②③④
二.填空题(共11小题,满分44分)
10.如图,正方形ABCD,延长AB至E,使AE=BD,则∠BCE的度数 .
11.正方形ABCD的边长为4,则图中阴影部分的面积为 .
12.正方形的对角线长为2cm,则它的周长为 cm.
13.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 .
14.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
15.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB= .
16.如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于 .
17.如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD= 时,四边形MENF是正方形.
18. ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: ,使得 ABCD为正方形.
19.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为 .
20.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是 (只填写序号).
三.解答题(共4小题,满分40分)
21.如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,BE与AF相交于点O,P是BF的中点,连接OP.
(1)试判断AF与BE的关系,并证明你的结论;
(2)若AB=5,AE=2,求OP的长.
22.如图,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.
23.已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
24.如图,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,ED=EC.求证:四边形DFCE是正方形.
25.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC,垂足为点E,GF⊥BC,垂足为点F,连接AG.写出线段AG,GE,GF之间的数量关系,并说明理由.
26.已知,如图,在正方形ABCD中,E为对角线AC上一点,EG⊥ED交BC于点G,EF⊥BC,垂足为F.
(1)求证:BF=GF;
(2)如图,若DE=DH,AB=8.
①求证:CG=FG;
②求EH的值.
参考答案
一.选择题(共9小题,满分40分)
1.解:∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
故选:C.
2.解:如图,连接AP,AN,点A是正方形的对角线的交点.
则AP=AN,∠APF=∠ANE=45°,
∵∠PAF+∠FAN=∠FAN+∠NAE=90°,
∴∠PAF=∠NAE,
∴△PAF≌△NAE,
∴四边形AENF的面积等于△NAP的面积,
而△NAP的面积是正方形的面积的,而正方形的面积为4,
∴四边形AENF的面积为1cm2,四块阴影面积的和为4cm2.
故选:B.
3.解:如图所示:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=,则B2C2=()1,
同理可得:B3C3==()2,
故正方形AnBn nDn的边长是:()n﹣1.
则正方形A2021B2021C2021D2021的边长是:()2020.
故选:D.
4.解:如图,连接BD,
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,BC=EC,
∴∠EBC=∠BEC=(180°﹣∠BCE)=15°
∵∠BCM=∠BCD=45°,
∴∠BMC=180°﹣(∠BCM+∠EBC)=120°,
∴∠AMB=180°﹣∠BMC=60°
∵AC是线段BD的垂直平分线,M在AC上,
∴∠AMD=∠AMB=60°
故选:B.
5.解:A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;
B、对角线互相垂直的平行四边形是菱形;故本选项错误;
C、对角线互相平分的四边形是平行四边形;故本选项正确;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误;
故选:C.
6.解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意;
C、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意.
故选:B.
7.解:如图,∵点E,F,G,H分别是四边形ABCD各边的中点,且四边形EFGH是正方形,
∴EF=EH,EF⊥EH,
∵BD=2EF,AC=2EH,
∴AC=BD,AC⊥BD,
即四边形ABCD满足对角线相等且垂直,
选项D满足题意.
故选:D.
8.解:A、一组对边平行另一组对边相等的四边形可以是等腰梯形,可以是平行四边形,故选项A不合题意;
B、对角线互相垂直平分的四边形是菱形,故选项B符合题意;
C、对角线相等的平行四边形是矩形,故选项C不合题意;
D、对角线互相垂直平分且相等的四边形是正方形,故选项D不合题意;
故选:B.
9.解:如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,
∴①不正确;
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,
∴③正确;
在△AEO和△AFO中,
,
∴△AE0≌△AF0(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,
∴②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,
∴④正确.
综上,可得正确的是:②③④.
故选:B.
二.填空题(共11小题,满分44分)
10.解:∵四边形ABCD是正方形,
∴∠BAC=∠ACB=45°,
∵AE=AC,
∴∠ACE=∠E=(180°﹣45°)=67.5°,
∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°.
故答案为:22.5°.
11.解:由图形可得:
S阴影= S正方形ABCD=×4×4=8.
故答案为:8.
12.解:如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠B=90°,
∴AB2+BC2=AC2,
∴2AB2=(2)2,
∴AB=2cm,
∴正方形ABCD的周长=4×2=8(cm);
故答案为:8.
13.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∵等边三角形ADE,
∴AD=AE,∠DAE=∠AED=60°.
∠BAE=∠BAD+∠DAE=90°+60°=150°,
AB=AE,
∠AEB=∠ABE=(180°﹣∠BAE)÷2=15°,
∠BED=∠DEA﹣∠AEB=60°﹣15°=45°.
故答案为:45°.
14.解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===2,
∴CH=,
故答案为:.
15.解:连接BD交AC于O,
∵四边形ABCD、AGFE是正方形,
∴AB=AD,AE=AG,∠DAB=∠EAG,
∴∠EAB=∠GAD,
在△AEB和△AGD中,
,
∴△EAB≌△GAD(SAS),
∴EB=GD,
∵四边形ABCD是正方形,AB=,
∴BD⊥AC,AC=BD=AB=2,
∴∠DOG=90°,OA=OD=BD=1,
∵AG=1,
∴OG=OA+AG=2,
∴GD==,
∴EB=.故答案为:.
16.解:在正方形ABCD中,
∵∠ABD=∠CBD=45°,
∵四边形MNPQ和AEFG均为正方形,
∴∠BEF=∠AEF=90°,∠BMN=∠QMN=90°,
∴△BEF与△BMN是等腰直角三角形,
∴FE=BE=AE=AB,BM=MN=QM,
同理DQ=MQ,
∴MN=BD=AB,
∴==,
故答案为:.
17.解:当AB:AD=1:2时,四边形MENF是正方形,
理由是:∵AB:AD=1:2,AM=DM,AB=CD,
∴AB=AM=DM=DC,
∵∠A=∠D=90°,
∴∠ABM=∠AMB=∠DMC=∠DCM=45°,
∴∠BMC=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°,
∴BM=CM,
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形,
即当AB:AD=1:2时,四边形MENF是正方形,
故答案为:1:2.
18.解:∵ ABCD的对角线AC与BD相交于点O,且AC⊥BD,
∴ ABCD是菱形,
当∠BAD=90°时, ABCD为正方形.
故答案为:∠BAD=90°.
19.解:∠ACB=90°时,四边形ADCF是正方形,
理由:∵E是AC中点,
∴AE=EC,
∵DE=EF,
∴四边形ADCF是平行四边形,
∵AD=DB,AE=EC,
∴DE=BC,
∴DF=BC,
∵CA=CB,
∴AC=DF,
∴四边形ADCF是矩形,
点D、E分别是边AB、AC的中点,
∴DE∥BC,
∵∠ACB=90°,
∴∠AED=90°,
∴矩形ADCF是正方形.
故答案为:∠ACB=90°.
20.解:有6种选法:(1)①②:由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(2)②③:由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误;
(3)①③:由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(4)②④:由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
(5)①④:由①得有一组邻边相等的平行四边形是菱形,由④得对角线互相垂直的平行四边形是菱形,所以不能得出平行四边形ABCD是正方形,错误;
(6)③④:由③得对角线相等的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
综上所述:错误的是:②③或①④;
故答案为:②③或①④.
三.解答题(共4小题,满分40分)
21.解:(1)AF=BE,理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ADC=90°,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴AF=BE;
(2)由(1)知∴△BAE≌△ADF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AOE=∠BOF=90°,
∵点P为BF的中点,
∴OP=BF,
∵BC=AB=CD=5,AE=DF=2,
∴CF=CD﹣DF=5﹣2=3,
∴BF===,
∴OP=.
22.证明:∵四边形ABCD是正方形,
∴AB=BC,
∠ABE=∠BCF=90°,
∵∠AOF=90°,∠AOB=90°,
∴∠BAE+∠OBA=90°,
又∵∠FBC+∠OBA=90°,
∴∠BAE=∠CBF(同角的余角相等),
在△ABE和△BCF中
∴,
∴△ABE≌△BCF(ASA).
∴BE=CF.
23.证明:∵BF∥CE,CF∥BE
∴四边形BECF是平行四边形,
又∵在矩形ABCD中,BE平分∠ABC,CE平分∠DCB
∴∠EBC=∠ECB=45°
∴∠BEC=90°,BE=CE
∴四边形BECF是正方形.
24.解:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
25.解:AG2=GE2+GF2,理由如下:
如图,连接CG,
∵四边形ABCD是正方形,
∴AB=BC,∠ABG=∠CBG,∠BCD=90°,
在△ABG和△CBG中,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,
∵GE⊥DC,垂足为点E,GF⊥BC,垂足为点F,
∴∠GEC=∠GFC=90°,
∴∠GEC=∠GFC=∠BCD=90°,
∴四边形CEGF是矩形,
∴GF=CE,
在Rt△CEG中,GC2=GE2+EC2,
∴AG2=GE2+GF2.
26.(1)证明:如图所示,连接EB,
∵四边形ABCD为正方形,
∴∠ACB=∠DCE,BC=CD.
又∵EC=EC,
∴△EBC≌△EDC(SAS),
∴EB=ED.
延长FE交AD于N,
∵∠NAE=45°,EF⊥BC,
∴∠NEA=45°,即AN=NE,
∵AB=AD,AD∥BC,即AB=NF,
∴ND=EF,
∵EG⊥ED,
∴∠FEG+∠EGF=∠FEG+∠NED,
∴∠EGF=∠NED,
∵∠EFG=∠END,
∴△EFG≌△DNE(AAS),
∴ED=EG,
∴EB=EG.
∵EF⊥BC,
∴BF=GF;
(2)①证明:如图所示,作GM⊥AC,垂足为M.
∵DE=DH,∠DEG=90°,
∴∠EDH=45°,
∴∠DEH=67.5°,
∴∠GEH=22.5°.
又∵∠FEC=45°,
∴∠FEG=22.5°,
∴∠FEG=∠GEM.
∵GF⊥EF,GM⊥EC,
∴GF=GM.
∵∠MCG=45°,
∴GC=GM=FG;
②解:∵AD∥BC,
由①可知,CG:FG:BF=:1:1,
∴.
即,
∴=,
∵BC=8,
∴AC=8,
∴CH=8﹣8,
∴AE=8﹣8,
∴EH=8﹣2×(8﹣8)=16﹣8.
