2021-2022学年北师大版八年级数学下册 1.1等腰三角形 同步自主提升训练(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册 1.1等腰三角形 同步自主提升训练(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 313.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 22:12:03 | ||
图片预览

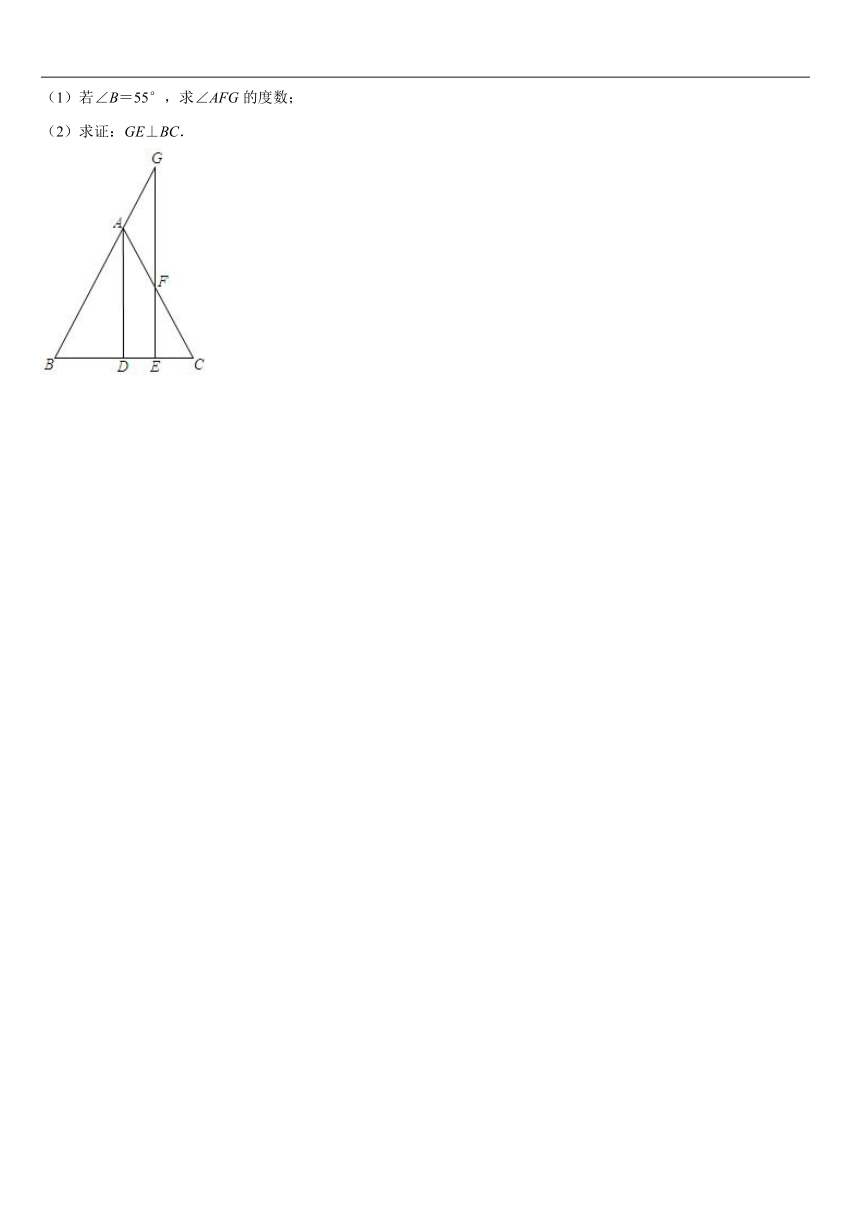
文档简介
2021-2022学年北师大版八年级数学下册《1-1等腰三角形》同步自主提升训练
1.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
2.下列说法中,正确的有( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个 B.2个 C.3个 D.4个
3.如图所示,在直角三角形ABC中,已知∠ACB=90°,点E是AB的中点,且DE⊥AB,DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( )
A.5 B.4 C.3 D.2
4.等腰三角形的一边为4,另一边为9,则这个三角形的周长为( )
A.17 B.22 C.13 D.17或22
5.若等腰三角形的顶角是大于60°的锐角,则底角度数可以是( )
A.30° B.45° C.55° D.65°
6.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,若∠BEC=90°,则∠ACE的度数( )
A.60° B.45° C.30° D.15°
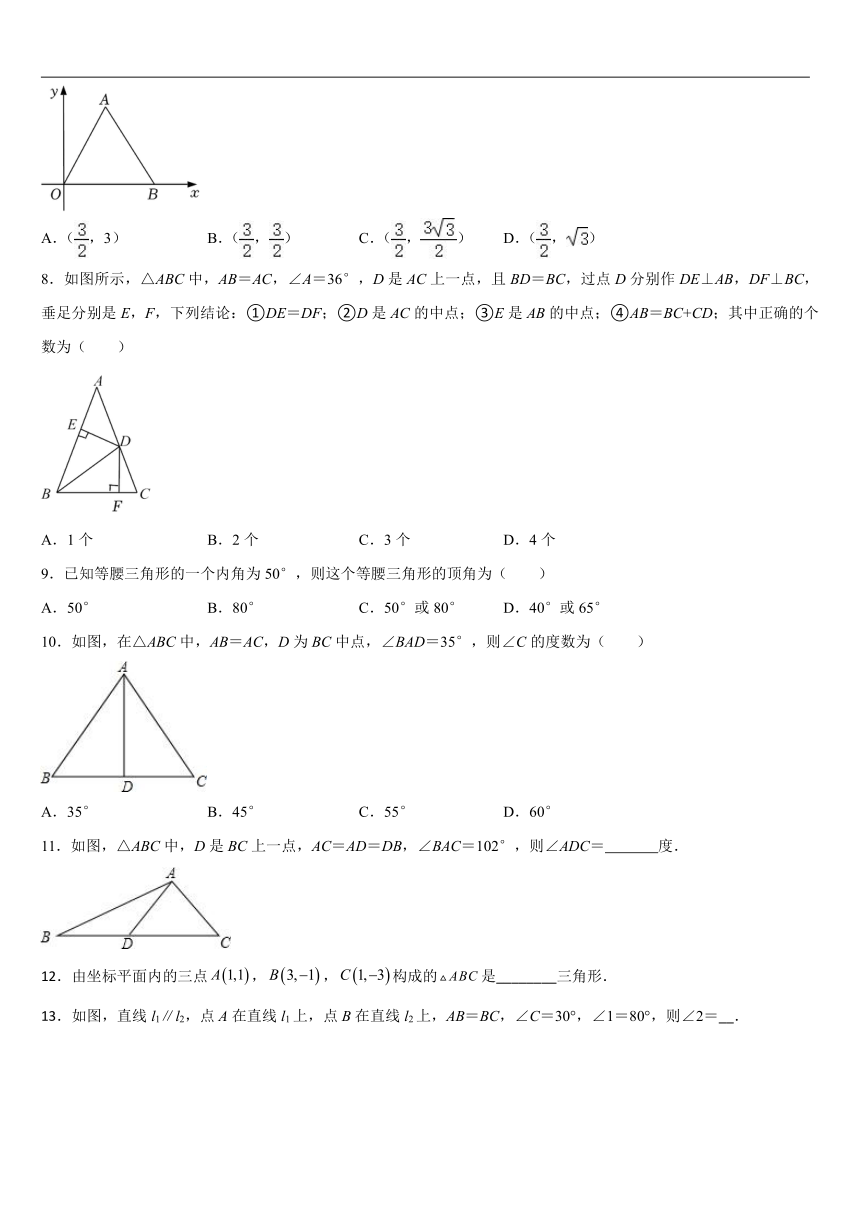
7.如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(3,0),则A点的坐标是( )
A.(,3) B.(,) C.(,) D.(,)
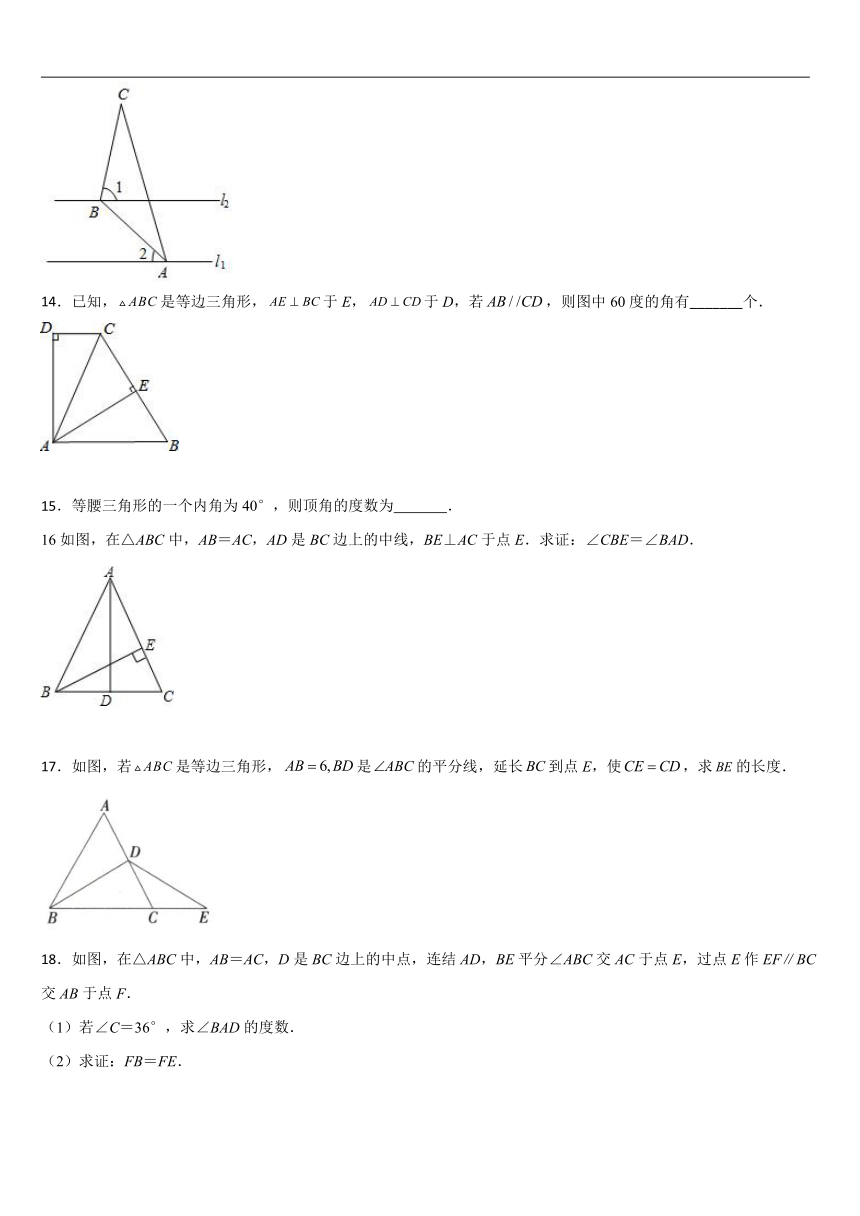
8.如图所示,△ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分别是E,F,下列结论:①DE=DF;②D是AC的中点;③E是AB的中点;④AB=BC+CD;其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
9.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
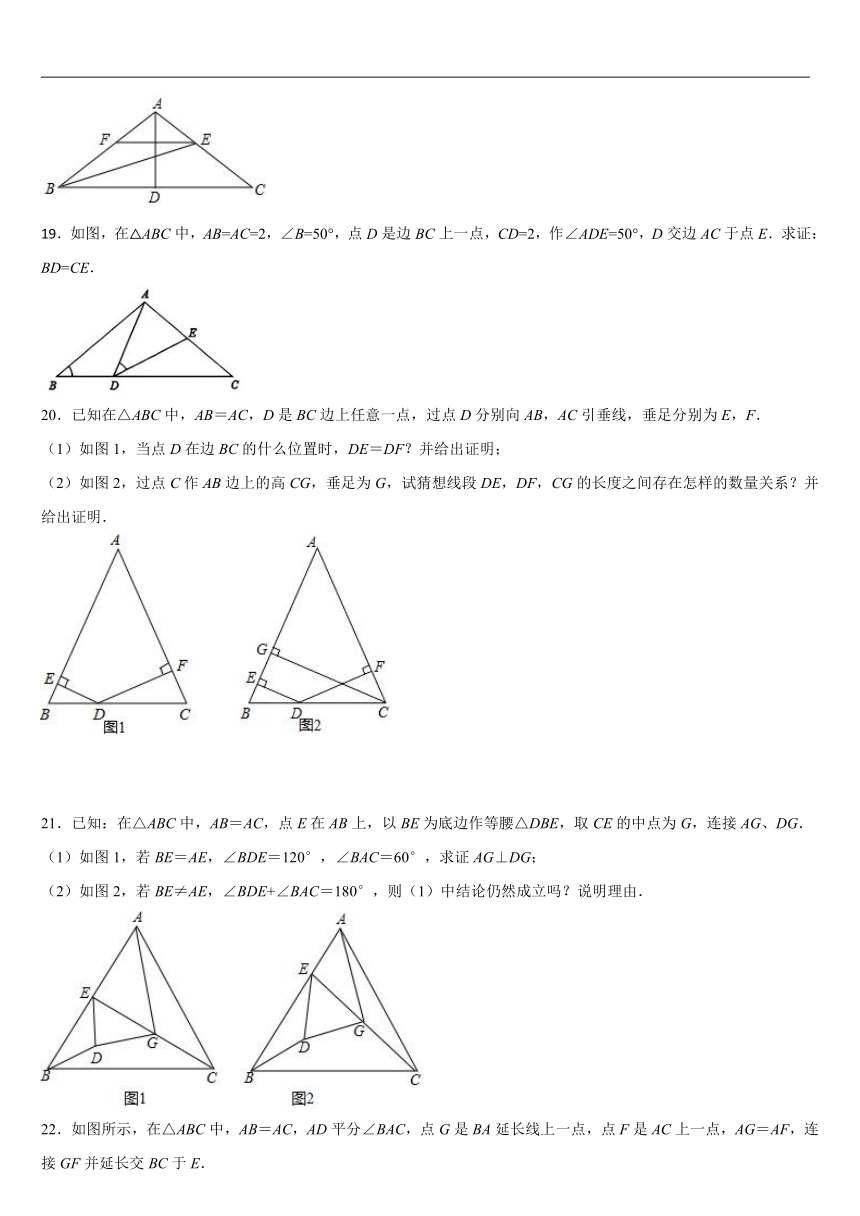
10.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
11.如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC= 度.
12.由坐标平面内的三点,,构成的是________三角形.
13.如图,直线l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2=__.
14.已知,是等边三角形,于E,于D,若,则图中60度的角有_______个.
15.等腰三角形的一个内角为40°,则顶角的度数为 .
16如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
17.如图,若是等边三角形,是的平分线,延长到点E,使,求的长度.
18.如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
19.如图,在△ABC中,AB=AC=2,∠B=50°,点D是边BC上一点,CD=2,作∠ADE=50°,D交边AC于点E.求证:BD=CE.
20.已知在△ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.
(1)如图1,当点D在边BC的什么位置时,DE=DF?并给出证明;
(2)如图2,过点C作AB边上的高CG,垂足为G,试猜想线段DE,DF,CG的长度之间存在怎样的数量关系?并给出证明.
21.已知:在△ABC中,AB=AC,点E在AB上,以BE为底边作等腰△DBE,取CE的中点为G,连接AG、DG.
(1)如图1,若BE=AE,∠BDE=120°,∠BAC=60°,求证AG⊥DG;
(2)如图2,若BE≠AE,∠BDE+∠BAC=180°,则(1)中结论仍然成立吗?说明理由.
22.如图所示,在△ABC中,AB=AC,AD平分∠BAC,点G是BA延长线上一点,点F是AC上一点,AG=AF,连接GF并延长交BC于E.
(1)若∠B=55°,求∠AFG的度数;
(2)求证:GE⊥BC.
参考答案
1.解:∵AD是△ABC的中线,AB=AC,∠CAD=20°,
∴∠CAB=2∠CAD=40°,∠B=∠ACB=(180°﹣∠CAB)=70°.
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°.
故选:B.
2.解:①等腰三角形的两腰相等,正确;
②等腰三角形的两底角相等,正确;③等腰三角形底边上的中线与底边上的高相等,正确;
④等腰三角形是轴对称图形,对称轴就是底边上的高所在的直线,正确.
故选:D.
3.解:如图,AB是腰长时,红色的4个点可以作为点C,
AB是底边时,黑色的4个点都可以作为点C,
所以,满足条件的点C的个数是4+4=8.
故选:B.
4.解:当腰长为4时,则三角形的三边长为:4、4、9;
∵4+4<9,∴不能构成三角形;
因此这个等腰三角形的腰长为9,则其周长=9+9+4=22.
故选:B.
5.解:∵∠1=125°,
∴∠ADE=180°﹣125°=55°,
∵DE∥BC,AB=AC,
∴AD=AE,∠C=∠AED,
∴∠AED=∠ADE=55°,
又∵∠C=∠AED,
∴∠C=55°.
故选:A.
6.解:∵等边三角形ABC中,AD⊥BC,
∴BD=CD,即:AD是BC的垂直平分线,
∵点E在AD上,
∴BE=CE,
∴∠EBC=∠ECB,
∵∠BEC=90°,
∴∠EBC=∠ECB=45°,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACE=∠ACB﹣∠ECB=15°,
故选:D.
7.解:过点A作AC⊥x轴于点C,如图所示.
∵△AOB是等边三角形,B点的坐标是(3,0),
∴OA=OB=3,OC=BC=OB=,
在Rt△ACO中,OA=3,OC=,
∴AC===,
∴点A的坐标为(,).
故选:C.
8.解:①∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,
∵BD=BC,
∴∠BDC=∠BCD=72°,
∵∠BDC=∠A+∠ABD,
∴∠ABD=36°,
∴∠ABD=∠CBD,
∴BD是∠ABC的角平分线,
∴DE=DF,故①正确.
②因为∠A=∠ABD=36°,
∴AD=BD,但BD≠CD,故②错误;
③∵AD=BD,DE⊥AB,
∴DE垂直平分AB,③正确;
∴④∵BD=BC,AD=BD,
∴AD=BD=BC,
又∵AB=AC,
∴AB=AD+CD=BC+CD,故④正确;
①③④正确.
故选:C.
9.解:如图所示,△ABC中,AB=AC.
有两种情况:
①顶角∠A=50°;
②当底角是50°时,
∵AB=AC,
∴∠B=∠C=50°,
∵∠A+∠B+∠C=180°,
∴∠A=180°﹣50°﹣50°=80°,
∴这个等腰三角形的顶角为50°和80°.
故选:C.
10.解:AB=AC,D为BC中点,
∴AD是∠BAC的平分线,∠B=∠C,
∵∠BAD=35°,
∴∠BAC=2∠BAD=70°,
∴∠C=(180°﹣70°)=55°.
故选:C.
11.解:∵AC=AD=DB,
∴∠B=∠BAD,∠ADC=∠C,
设∠ADC=α,
∴∠B=∠BAD=,
∵∠BAC=102°,
∴∠DAC=102°﹣,
在△ADC中,
∵∠ADC+∠C+∠DAC=180°,
∴2α+102°﹣=180°,
解得:α=52°.
故答案为:52.
12.等腰直角
【分析】
在网格坐标系中画出三角形,由每一个小的网格是正方形,根据图形的轴对称的性质可得答案;
【详解】
解:如图,
由每一个小的网格是正方形,
关于直线成轴对称,都是等腰直角三角形,
所以:是等腰直角三角形,
故答案为:等腰直角.
【点睛】
本题考查的是坐标与图形,轴对称图形的性质,等腰直角三角形的定义,掌握以上知识是解题的关键.
13.40°
【分析】
延长CB交l1于点D,得出∠1=∠3=80°,根据等腰三角形的性质和三角形内角和可求∠2.
【详解】
解:如图,延长CB交l1于点D,
∵AB=BC,∠C=30°,
∴∠C=∠4=30°,
∵l1∥l2,∠1=80°,
∴∠1=∠3=80°,
∵∠C+∠3+∠2+∠4=180°,即30°+80°+∠2+30°=180°,
∴∠2=40°.
故答案为:40°.
【点睛】
本题考查了等腰三角形的性质、平行线的性质、三角形内角和,解题关键是熟记相关性质,准确进行推理与计算.
14.5
【分析】
先根据等边三角形的性质得到∠B=∠ACB=∠BAC=60°,∠CAE=∠BAE=30°,再由平行线的性质得到∠AD=∠CAB=60°,从而得到∠DAC=30°,∠DAE=∠DAC+∠CAE=60°,即可求解.
【详解】
解:∵△ABC是等边三角形,AE⊥BC,
∴∠B=∠ACB=∠BAC=60°,∠CAE=∠BAE=30°,
∵AB∥CD,
∴∠ACD=∠CAB=60°,
∵AD⊥CD,
∴∠D=90°,
∴∠DAC=30°,
∴∠DAE=∠DAC+∠CAE=60°,
∴60度的角一共有5个,
故答案为:5.
【点睛】
本题主要考查了等边三角形的性质,平行线的性质,三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.
15.解:当这个角是顶角时,则顶角的度数为40°,当这个角是底角时,则顶角的度数180°﹣40°×2=100°,
故其顶角的度数为100°或40°.
故填100°或40°.
16.证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∠BAD=∠CAD,
∵BE⊥AC,
∴∠BEC=∠ADC=90°.,
∴∠CBE=90°﹣∠C,∠CAD=90°﹣∠C,
∴∠CBE=∠CAD.,
∴∠CBE=∠BAD.
17.9
【分析】
首先由等边三角形的定义可得,然后利用“三线合一”的性质求出,即可得出结论.
【详解】
解:∵是等边三角形,
∴,
∵是的平分线,
∴,
∵,
∴,
∴.
【点睛】
本题考查等边三角形的性质,理解等边三角形的基本性质是解题关键.
18(1)54°,(2)见解析
【分析】
(1)利用等腰三角形的三线合一的性质证明∠ADB=90°,再利用等腰三角形的性质求出∠ABC即可解决问题.
(2)利用角平分线性质和平行线性质证明∠FBE=∠FEB即可.
【详解】
解:(1)∵AB=AC,
∴∠C=∠ABC,
∵∠C=36°,
∴∠ABC=36°,
∵D为BC的中点,
∴AD⊥BC,
∴∠BAD=90°﹣∠ABC=90°﹣36°=54°.
(2)∵BE平分∠ABC,
∴∠ABE=∠EBC,
又∵EF∥BC,
∴∠EBC=∠BEF,
∴∠EBF=∠FEB,
∴BF=EF.
【点睛】
本题考查等腰三角形的性质,平行线的性质等知识,解题的关键是熟练掌握等腰三角形的性质和判定,熟练运用平行线进行角的推导和证明.
19.见解析
【分析】
根据“”证明,即可得出结论.
【详解】
证明:∵,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
,
∴,
∴.
【点睛】
本题考查了全等三角形的判定与性质,熟知全等三角形的判定定理是解本题的关键.
20.解:(1)当点D在BC的中点上时,DE=DF,
证明:∵D为BC中点,
∴BD=CD,
∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF.
(2)CG=DE+DF
证明:连接AD,
∵S三角形ABC=S三角形ADB+S三角形ADC,
∴AB×CG=AB×DE+AC×DF,
∵AB=AC,
∴CG=DE+DF.
21.(1)证明:延长DG至H,使GH=GD,连接AD,AH,CH,如图1,
∵G为CE的中点,
∴GC=GE,
在△CHG和△EDG中,
,
∴△CHG≌△EDG(SAS),
∴CH=ED,∠HCG=∠DEG,
∵BD=ED,∠BDE=120°,
∴∠BED=∠EBD=30°,
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∵AE=BE,
∴CE⊥AB,
∴∠BED+∠DEG=90°,∠BAC+∠ACE=90°,
∴∠HCG=∠DEG=60°,∠ACE=30°,
∴∠ACH=30°,
∴∠ABD=∠ACH,
在△ABD和△ACH中,
,
∴△ABD≌△ACH(SAS),
∴AD=AH,
∵HG=DG,
∴AG⊥DG;
(2)解:(1)中结论仍然成立.
理由:延长DG至M,使GM=GD,连接AD,AM,CM,如图2,
∵G为CE的中点,
∴GC=GE,
在△CMG和△EDG中,
,
∴△CMG≌△EDG(SAS),
∴CM=ED,∠MCG=∠DEG,
∵BD=ED,
∴∠BED=∠EBD=180°﹣∠BDE,
∵∠BDE+∠BAC=180°,
∴∠BAC=180°﹣∠BDE,
∴∠BAC=2∠BED=2∠EBD,
∵∠BEC=∠BED+∠DEG=∠BAC+∠ACE,
∴∠BED+∠MCG=∠BAC+∠ACE,
∵∠MCG=∠ACM+∠ACE,
∴∠BED+∠ACM+∠ACE=2∠BED+∠ACE,
∴∠ACM=∠BED=∠ABD,
在△ABD和△ACM中,
,
∴△ABD≌△ACM(SAS),
∴AD=AM,
∵MG=DG,
∴AG⊥DG.
22.(1)解:∵AB=AC,
∴∠B=∠C=55°,
∴∠GAF=∠B+∠C=110°,
∵AG=AF,
∴∠AFG=(180°﹣110°)=35°.
(2)证明:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°
∴∠BAD=∠CAD=90°﹣55°=35°,
∴∠DAC=∠AFG,
∴AD∥FG,
∴GE⊥BC.
1.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
2.下列说法中,正确的有( )
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个 B.2个 C.3个 D.4个
3.如图所示,在直角三角形ABC中,已知∠ACB=90°,点E是AB的中点,且DE⊥AB,DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( )
A.5 B.4 C.3 D.2
4.等腰三角形的一边为4,另一边为9,则这个三角形的周长为( )
A.17 B.22 C.13 D.17或22
5.若等腰三角形的顶角是大于60°的锐角,则底角度数可以是( )
A.30° B.45° C.55° D.65°
6.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,若∠BEC=90°,则∠ACE的度数( )
A.60° B.45° C.30° D.15°
7.如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(3,0),则A点的坐标是( )
A.(,3) B.(,) C.(,) D.(,)
8.如图所示,△ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分别是E,F,下列结论:①DE=DF;②D是AC的中点;③E是AB的中点;④AB=BC+CD;其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
9.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
10.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
11.如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC= 度.
12.由坐标平面内的三点,,构成的是________三角形.
13.如图,直线l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2=__.
14.已知,是等边三角形,于E,于D,若,则图中60度的角有_______个.
15.等腰三角形的一个内角为40°,则顶角的度数为 .
16如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
17.如图,若是等边三角形,是的平分线,延长到点E,使,求的长度.
18.如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
19.如图,在△ABC中,AB=AC=2,∠B=50°,点D是边BC上一点,CD=2,作∠ADE=50°,D交边AC于点E.求证:BD=CE.
20.已知在△ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.
(1)如图1,当点D在边BC的什么位置时,DE=DF?并给出证明;
(2)如图2,过点C作AB边上的高CG,垂足为G,试猜想线段DE,DF,CG的长度之间存在怎样的数量关系?并给出证明.
21.已知:在△ABC中,AB=AC,点E在AB上,以BE为底边作等腰△DBE,取CE的中点为G,连接AG、DG.
(1)如图1,若BE=AE,∠BDE=120°,∠BAC=60°,求证AG⊥DG;
(2)如图2,若BE≠AE,∠BDE+∠BAC=180°,则(1)中结论仍然成立吗?说明理由.
22.如图所示,在△ABC中,AB=AC,AD平分∠BAC,点G是BA延长线上一点,点F是AC上一点,AG=AF,连接GF并延长交BC于E.
(1)若∠B=55°,求∠AFG的度数;
(2)求证:GE⊥BC.
参考答案
1.解:∵AD是△ABC的中线,AB=AC,∠CAD=20°,
∴∠CAB=2∠CAD=40°,∠B=∠ACB=(180°﹣∠CAB)=70°.
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°.
故选:B.
2.解:①等腰三角形的两腰相等,正确;
②等腰三角形的两底角相等,正确;③等腰三角形底边上的中线与底边上的高相等,正确;
④等腰三角形是轴对称图形,对称轴就是底边上的高所在的直线,正确.
故选:D.
3.解:如图,AB是腰长时,红色的4个点可以作为点C,
AB是底边时,黑色的4个点都可以作为点C,
所以,满足条件的点C的个数是4+4=8.
故选:B.
4.解:当腰长为4时,则三角形的三边长为:4、4、9;
∵4+4<9,∴不能构成三角形;
因此这个等腰三角形的腰长为9,则其周长=9+9+4=22.
故选:B.
5.解:∵∠1=125°,
∴∠ADE=180°﹣125°=55°,
∵DE∥BC,AB=AC,
∴AD=AE,∠C=∠AED,
∴∠AED=∠ADE=55°,
又∵∠C=∠AED,
∴∠C=55°.
故选:A.
6.解:∵等边三角形ABC中,AD⊥BC,
∴BD=CD,即:AD是BC的垂直平分线,
∵点E在AD上,
∴BE=CE,
∴∠EBC=∠ECB,
∵∠BEC=90°,
∴∠EBC=∠ECB=45°,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACE=∠ACB﹣∠ECB=15°,
故选:D.
7.解:过点A作AC⊥x轴于点C,如图所示.
∵△AOB是等边三角形,B点的坐标是(3,0),
∴OA=OB=3,OC=BC=OB=,
在Rt△ACO中,OA=3,OC=,
∴AC===,
∴点A的坐标为(,).
故选:C.
8.解:①∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°,
∵BD=BC,
∴∠BDC=∠BCD=72°,
∵∠BDC=∠A+∠ABD,
∴∠ABD=36°,
∴∠ABD=∠CBD,
∴BD是∠ABC的角平分线,
∴DE=DF,故①正确.
②因为∠A=∠ABD=36°,
∴AD=BD,但BD≠CD,故②错误;
③∵AD=BD,DE⊥AB,
∴DE垂直平分AB,③正确;
∴④∵BD=BC,AD=BD,
∴AD=BD=BC,
又∵AB=AC,
∴AB=AD+CD=BC+CD,故④正确;
①③④正确.
故选:C.
9.解:如图所示,△ABC中,AB=AC.
有两种情况:
①顶角∠A=50°;
②当底角是50°时,
∵AB=AC,
∴∠B=∠C=50°,
∵∠A+∠B+∠C=180°,
∴∠A=180°﹣50°﹣50°=80°,
∴这个等腰三角形的顶角为50°和80°.
故选:C.
10.解:AB=AC,D为BC中点,
∴AD是∠BAC的平分线,∠B=∠C,
∵∠BAD=35°,
∴∠BAC=2∠BAD=70°,
∴∠C=(180°﹣70°)=55°.
故选:C.
11.解:∵AC=AD=DB,
∴∠B=∠BAD,∠ADC=∠C,
设∠ADC=α,
∴∠B=∠BAD=,
∵∠BAC=102°,
∴∠DAC=102°﹣,
在△ADC中,
∵∠ADC+∠C+∠DAC=180°,
∴2α+102°﹣=180°,
解得:α=52°.
故答案为:52.
12.等腰直角
【分析】
在网格坐标系中画出三角形,由每一个小的网格是正方形,根据图形的轴对称的性质可得答案;
【详解】
解:如图,
由每一个小的网格是正方形,
关于直线成轴对称,都是等腰直角三角形,
所以:是等腰直角三角形,
故答案为:等腰直角.
【点睛】
本题考查的是坐标与图形,轴对称图形的性质,等腰直角三角形的定义,掌握以上知识是解题的关键.
13.40°
【分析】
延长CB交l1于点D,得出∠1=∠3=80°,根据等腰三角形的性质和三角形内角和可求∠2.
【详解】
解:如图,延长CB交l1于点D,
∵AB=BC,∠C=30°,
∴∠C=∠4=30°,
∵l1∥l2,∠1=80°,
∴∠1=∠3=80°,
∵∠C+∠3+∠2+∠4=180°,即30°+80°+∠2+30°=180°,
∴∠2=40°.
故答案为:40°.
【点睛】
本题考查了等腰三角形的性质、平行线的性质、三角形内角和,解题关键是熟记相关性质,准确进行推理与计算.
14.5
【分析】
先根据等边三角形的性质得到∠B=∠ACB=∠BAC=60°,∠CAE=∠BAE=30°,再由平行线的性质得到∠AD=∠CAB=60°,从而得到∠DAC=30°,∠DAE=∠DAC+∠CAE=60°,即可求解.
【详解】
解:∵△ABC是等边三角形,AE⊥BC,
∴∠B=∠ACB=∠BAC=60°,∠CAE=∠BAE=30°,
∵AB∥CD,
∴∠ACD=∠CAB=60°,
∵AD⊥CD,
∴∠D=90°,
∴∠DAC=30°,
∴∠DAE=∠DAC+∠CAE=60°,
∴60度的角一共有5个,
故答案为:5.
【点睛】
本题主要考查了等边三角形的性质,平行线的性质,三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.
15.解:当这个角是顶角时,则顶角的度数为40°,当这个角是底角时,则顶角的度数180°﹣40°×2=100°,
故其顶角的度数为100°或40°.
故填100°或40°.
16.证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∠BAD=∠CAD,
∵BE⊥AC,
∴∠BEC=∠ADC=90°.,
∴∠CBE=90°﹣∠C,∠CAD=90°﹣∠C,
∴∠CBE=∠CAD.,
∴∠CBE=∠BAD.
17.9
【分析】
首先由等边三角形的定义可得,然后利用“三线合一”的性质求出,即可得出结论.
【详解】
解:∵是等边三角形,
∴,
∵是的平分线,
∴,
∵,
∴,
∴.
【点睛】
本题考查等边三角形的性质,理解等边三角形的基本性质是解题关键.
18(1)54°,(2)见解析
【分析】
(1)利用等腰三角形的三线合一的性质证明∠ADB=90°,再利用等腰三角形的性质求出∠ABC即可解决问题.
(2)利用角平分线性质和平行线性质证明∠FBE=∠FEB即可.
【详解】
解:(1)∵AB=AC,
∴∠C=∠ABC,
∵∠C=36°,
∴∠ABC=36°,
∵D为BC的中点,
∴AD⊥BC,
∴∠BAD=90°﹣∠ABC=90°﹣36°=54°.
(2)∵BE平分∠ABC,
∴∠ABE=∠EBC,
又∵EF∥BC,
∴∠EBC=∠BEF,
∴∠EBF=∠FEB,
∴BF=EF.
【点睛】
本题考查等腰三角形的性质,平行线的性质等知识,解题的关键是熟练掌握等腰三角形的性质和判定,熟练运用平行线进行角的推导和证明.
19.见解析
【分析】
根据“”证明,即可得出结论.
【详解】
证明:∵,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
,
∴,
∴.
【点睛】
本题考查了全等三角形的判定与性质,熟知全等三角形的判定定理是解本题的关键.
20.解:(1)当点D在BC的中点上时,DE=DF,
证明:∵D为BC中点,
∴BD=CD,
∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF.
(2)CG=DE+DF
证明:连接AD,
∵S三角形ABC=S三角形ADB+S三角形ADC,
∴AB×CG=AB×DE+AC×DF,
∵AB=AC,
∴CG=DE+DF.
21.(1)证明:延长DG至H,使GH=GD,连接AD,AH,CH,如图1,
∵G为CE的中点,
∴GC=GE,
在△CHG和△EDG中,
,
∴△CHG≌△EDG(SAS),
∴CH=ED,∠HCG=∠DEG,
∵BD=ED,∠BDE=120°,
∴∠BED=∠EBD=30°,
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∵AE=BE,
∴CE⊥AB,
∴∠BED+∠DEG=90°,∠BAC+∠ACE=90°,
∴∠HCG=∠DEG=60°,∠ACE=30°,
∴∠ACH=30°,
∴∠ABD=∠ACH,
在△ABD和△ACH中,
,
∴△ABD≌△ACH(SAS),
∴AD=AH,
∵HG=DG,
∴AG⊥DG;
(2)解:(1)中结论仍然成立.
理由:延长DG至M,使GM=GD,连接AD,AM,CM,如图2,
∵G为CE的中点,
∴GC=GE,
在△CMG和△EDG中,
,
∴△CMG≌△EDG(SAS),
∴CM=ED,∠MCG=∠DEG,
∵BD=ED,
∴∠BED=∠EBD=180°﹣∠BDE,
∵∠BDE+∠BAC=180°,
∴∠BAC=180°﹣∠BDE,
∴∠BAC=2∠BED=2∠EBD,
∵∠BEC=∠BED+∠DEG=∠BAC+∠ACE,
∴∠BED+∠MCG=∠BAC+∠ACE,
∵∠MCG=∠ACM+∠ACE,
∴∠BED+∠ACM+∠ACE=2∠BED+∠ACE,
∴∠ACM=∠BED=∠ABD,
在△ABD和△ACM中,
,
∴△ABD≌△ACM(SAS),
∴AD=AM,
∵MG=DG,
∴AG⊥DG.
22.(1)解:∵AB=AC,
∴∠B=∠C=55°,
∴∠GAF=∠B+∠C=110°,
∵AG=AF,
∴∠AFG=(180°﹣110°)=35°.
(2)证明:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°
∴∠BAD=∠CAD=90°﹣55°=35°,
∴∠DAC=∠AFG,
∴AD∥FG,
∴GE⊥BC.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
