17.1.1勾股定理证明方法及基础运用 课件(共31页)
文档属性
| 名称 | 17.1.1勾股定理证明方法及基础运用 课件(共31页) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 19:49:01 | ||
图片预览



文档简介
(共31张PPT)
17.1 勾股定理
人教版八下数学
第1课时 勾股定理证法及基础运用
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
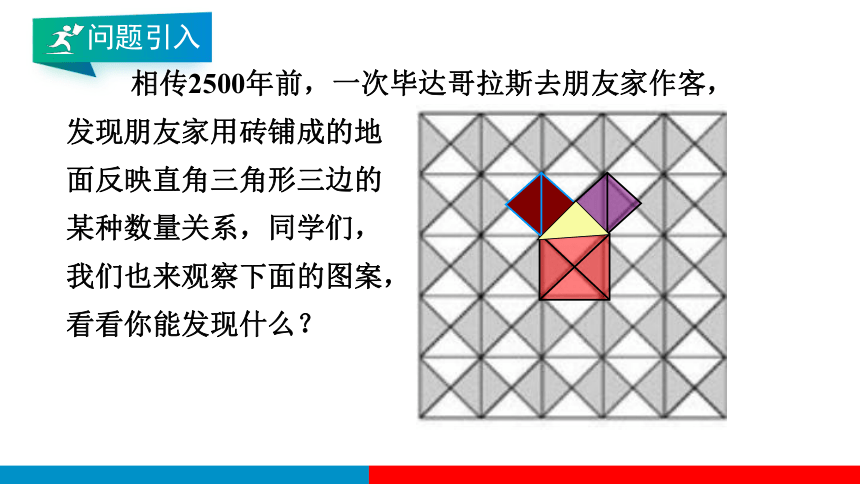
相传2500年前,一次毕达哥拉斯去朋友家作客,
发现朋友家用砖铺成的地
面反映直角三角形三边的
某种数量关系,同学们,
我们也来观察下面的图案,
看看你能发现什么?
问题引入
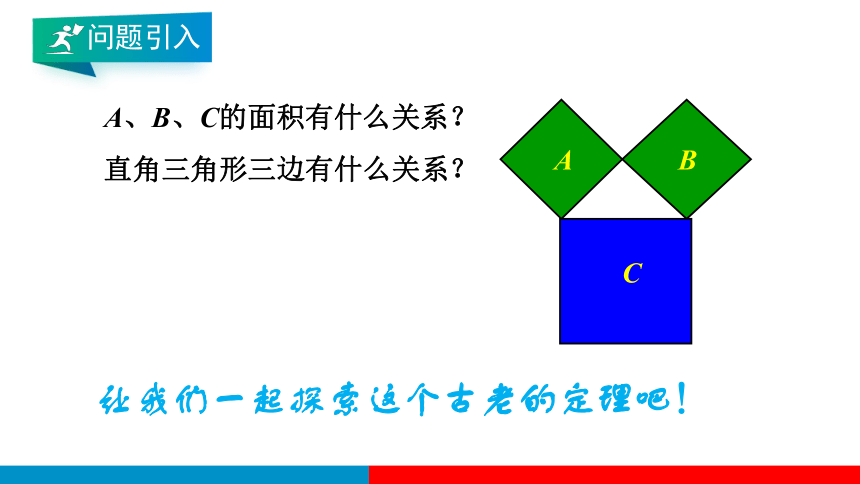
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
A
B
C
让我们一起探索这个古老的定理吧!
问题引入
勾股定理
1
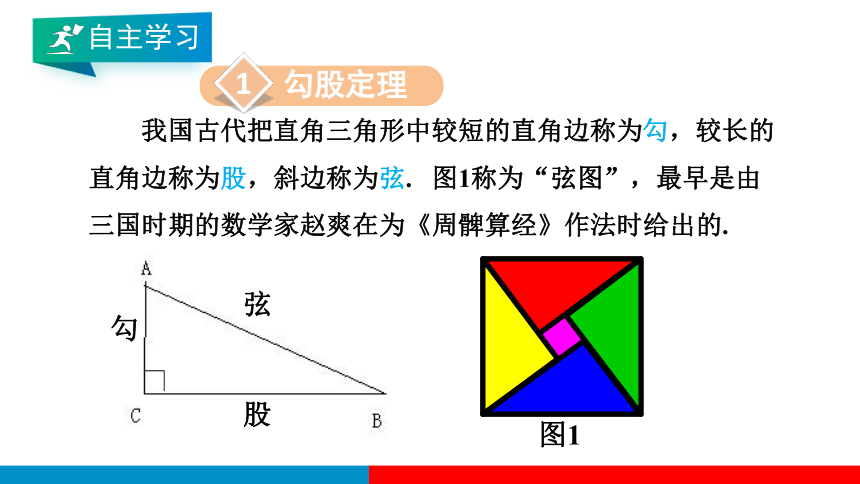
我国古代把直角三角形中较短的直角边称为勾,较长的
直角边称为股,斜边称为弦. 图1称为“弦图”,最早是由
三国时期的数学家赵爽在为《周髀算经》作法时给出的.
弦
股
勾
图1
自主学习
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
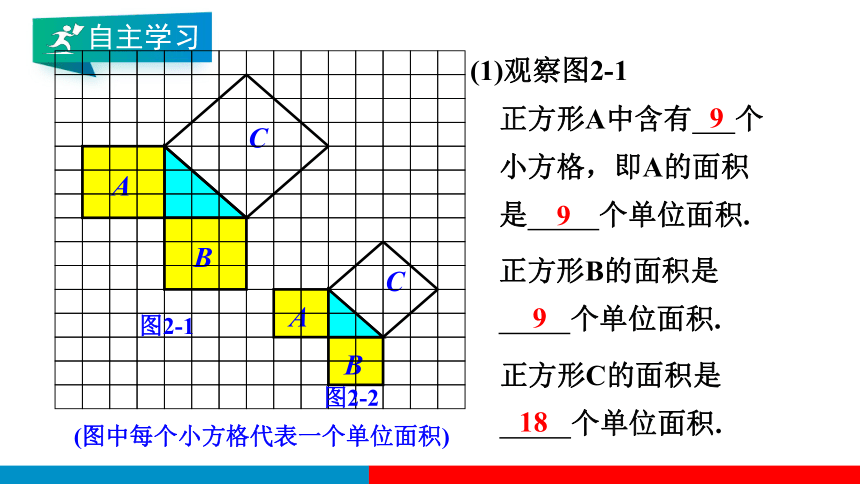
(1)观察图2-1
正方形A中含有 个
小方格,即A的面积
是 个单位面积.
正方形B的面积是
个单位面积.
正方形C的面积是
个单位面积.
9
9
9
18
自主学习
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
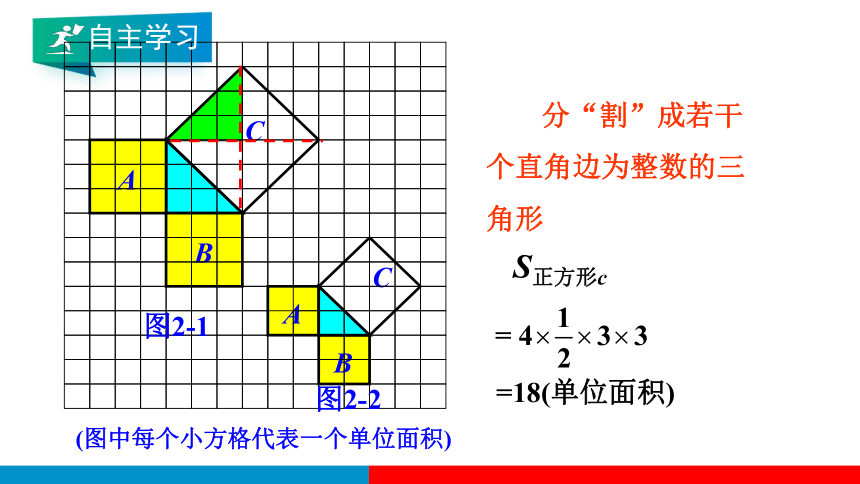
分“割”成若干个直角边为整数的三角形
=18(单位面积)
S正方形c
自主学习
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
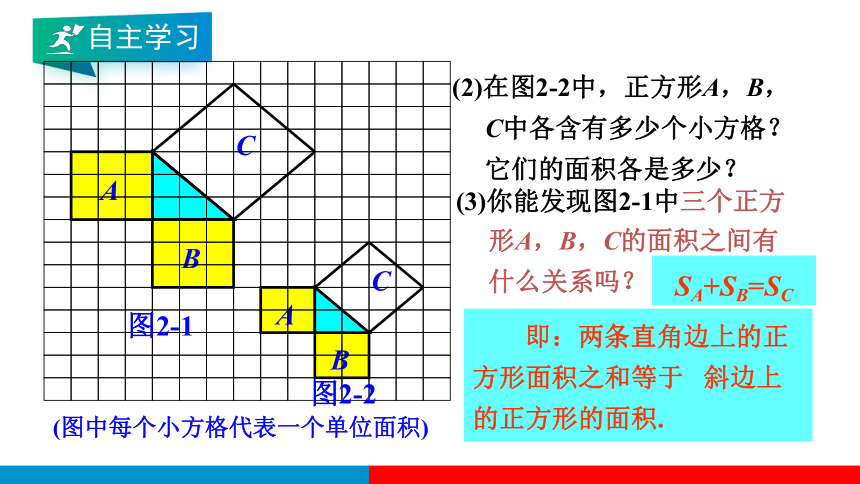
(2)在图2-2中,正方形A,B,
C中各含有多少个小方格?
它们的面积各是多少?
(3)你能发现图2-1中三个正方
形A,B,C的面积之间有
什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积.
自主学习
A
B
C
a
c
b
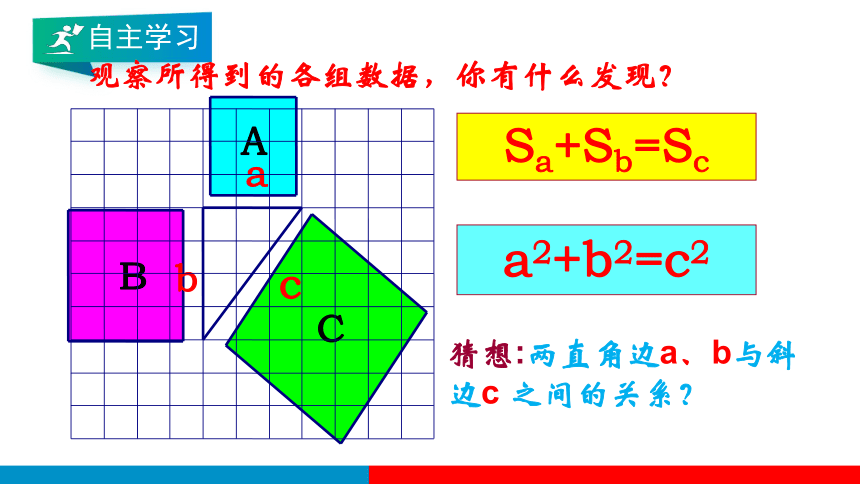
Sa+Sb=Sc
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
自主学习
┏
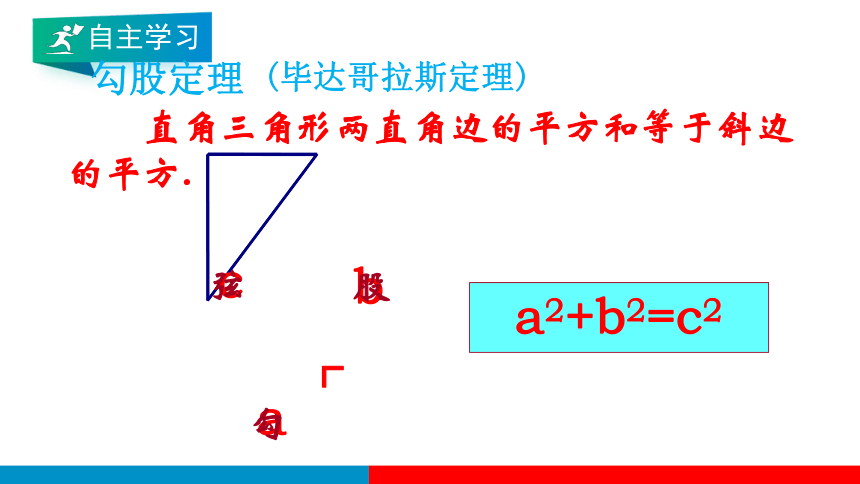
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
自主学习
定义:直角三角形两直角边的平方和等于斜边的平方.
如果用a,b和c分别表示直角三角形的两直角边
和斜边,那么a2+b2=c2.
数学表达式:
在Rt△ABC中,∠C=90°,AB=c,AC=b,
BC=a,则a2+b2=c2.
自主学习
a
b
b
c
a
b
c
a
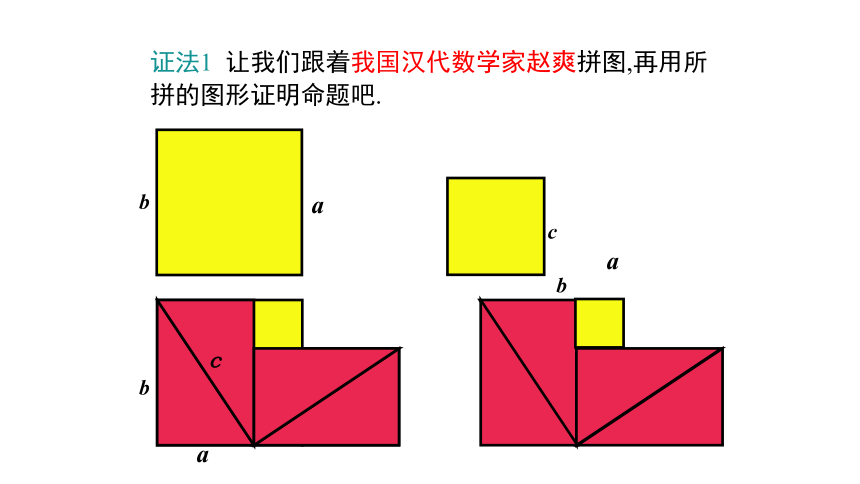
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽.
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
自主学习
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
自主学习
a
a
b
b
c
c
∴a2 + b2 = c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
自主学习
例 1
分清斜边和直角边.因为在Rt△ABC中,a,b,
c是三边,所以可以用勾股定理解决问题.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的
对边分别是a,b,c.
(1)已知a=b=6,求c;
(2)已知c=3,b=2,求a;
(3)已知a∶b=2∶1,c=5,求b.
导引:
典例分析
(1)∵∠C=90°,a=b=6,
∴由勾股定理,得
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=
解:
典例分析
1.设直角三角形的两条直角边长分别为a和b,
斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
(1)
(2)
(3)
解:
课堂练习
勾股定理与面积的关系
2
在一张纸上画4个与图所示的全等的直角三边形,并把它们剪下来.如图所示,用这四个直角三角形进行拼摆,将得到一个以a+b为边长的大正方形和以直角形斜边c为边长的小正方形.
自主学习
归 纳
观察图形,容易得到大正方形的边长为 a+b,所以
大正方形的面积是(a+b)2.又因为大正方形是由4个全等
的直角三角形和中间的正方形拼成的,所以大正方形的
面积又可表示成 ab×4+c2. 因此有(a+b)2= ab×4+
c2.整理得a2+b2=c2,即a、b、c为边的直角三角形满足
两直角边的平方和等于斜边的平方.
自主学习
观察如图所示的图形,回答问题:
(1)如图①,△DEF为直角三角形,正方形 P的面积为9,正方形Q的面积为15,则正方形为________;
(2)如图②,分别以直角三角形ABC的三边长为直径向三角形外作三个半圆,则这三个半圆形的面积之间的关系式是________; (用图中字母表示)
(3)如图③,如果直角三角形两直
角边的长分别为3和4,分别以
直角三角形的三边长为直径作
半圆,请你利用(2)中得出的结论求阴影部分的面积.
例2
典例分析
(1)根据正方形的面积公式,结合勾股定理可得
DF2=DE2+EF2,即正方形M的面积=9+15=24;
(2)
另外由勾股定理可知AC2+BC2=AB2,所以S1+S2=S3;
(3)阴影部分的面积=两个小半圆形的面积和+直角三角
形的面积-大半圆形的面积,由(2)可知两个小半圆形
的面积和=大半圆形的面积,所以阴影部分的面积=
直角三角形的面积.
典例分析
(1)24
(2)S1+S2=S3
(3)设两个小半圆形的面积分别为S1,S2,大半圆
形的面积为S3,三角形的面积为S△,
则S阴影=S1+S2+S△-S3
=S△= ×3×4=6.
解:
典例分析
1.
如图,图中所有的三角形都是直角三角形,四边
形都是正方形.已知正方形A,B,C,D的边长分
别是12,16,9,12,求最大正方形E的面积.
SE=(122+162)+(92+122)
=400+225
=625.
解:
课堂练习
勾股定理
1. 勾股定理的适用条件:直角三角形;它反映了直角
三角形三边关系.
2.由勾股定理的基本关系式:a2+b2=c2可得到一些
变形关系式:c2=a2+b2=(a+b)2-2ab=(a-b)2
+2ab;a2=c2-b2=(c+b)(c-b)等.
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1) 已知a=12,b=5,求c;
(2) 已知a=3,c=4,求b;
(3) 已知c=10,b=9,求a.
解:
备选习题
2.一木杆在离地面3 m处折断,木杆顶端落在离木杆底端
4 m处.木杆折断之前有多高?
解:由题意得,图中直角三角形斜边长为 =5 (m),
∴木杆折断之前有3+5=8 (m).
备选习题
3.如图,一个圆锥的高AO=2.4,底面半径OB=0.7. AB的
长是多少?
解:在Rt△ABO中,AO=2.4,OB=0.7,由勾股定理得
AB=
故AB的长为2.5.
备选习题
https://www.21cnjy.com/help/help_extract.php
17.1 勾股定理
人教版八下数学
第1课时 勾股定理证法及基础运用
精品同步教学课件
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
相传2500年前,一次毕达哥拉斯去朋友家作客,
发现朋友家用砖铺成的地
面反映直角三角形三边的
某种数量关系,同学们,
我们也来观察下面的图案,
看看你能发现什么?
问题引入
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
A
B
C
让我们一起探索这个古老的定理吧!
问题引入
勾股定理
1
我国古代把直角三角形中较短的直角边称为勾,较长的
直角边称为股,斜边称为弦. 图1称为“弦图”,最早是由
三国时期的数学家赵爽在为《周髀算经》作法时给出的.
弦
股
勾
图1
自主学习
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(1)观察图2-1
正方形A中含有 个
小方格,即A的面积
是 个单位面积.
正方形B的面积是
个单位面积.
正方形C的面积是
个单位面积.
9
9
9
18
自主学习
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
分“割”成若干个直角边为整数的三角形
=18(单位面积)
S正方形c
自主学习
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(2)在图2-2中,正方形A,B,
C中各含有多少个小方格?
它们的面积各是多少?
(3)你能发现图2-1中三个正方
形A,B,C的面积之间有
什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积.
自主学习
A
B
C
a
c
b
Sa+Sb=Sc
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
自主学习
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
自主学习
定义:直角三角形两直角边的平方和等于斜边的平方.
如果用a,b和c分别表示直角三角形的两直角边
和斜边,那么a2+b2=c2.
数学表达式:
在Rt△ABC中,∠C=90°,AB=c,AC=b,
BC=a,则a2+b2=c2.
自主学习
a
b
b
c
a
b
c
a
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽.
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
自主学习
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
自主学习
a
a
b
b
c
c
∴a2 + b2 = c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
自主学习
例 1
分清斜边和直角边.因为在Rt△ABC中,a,b,
c是三边,所以可以用勾股定理解决问题.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的
对边分别是a,b,c.
(1)已知a=b=6,求c;
(2)已知c=3,b=2,求a;
(3)已知a∶b=2∶1,c=5,求b.
导引:
典例分析
(1)∵∠C=90°,a=b=6,
∴由勾股定理,得
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=
解:
典例分析
1.设直角三角形的两条直角边长分别为a和b,
斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
(1)
(2)
(3)
解:
课堂练习
勾股定理与面积的关系
2
在一张纸上画4个与图所示的全等的直角三边形,并把它们剪下来.如图所示,用这四个直角三角形进行拼摆,将得到一个以a+b为边长的大正方形和以直角形斜边c为边长的小正方形.
自主学习
归 纳
观察图形,容易得到大正方形的边长为 a+b,所以
大正方形的面积是(a+b)2.又因为大正方形是由4个全等
的直角三角形和中间的正方形拼成的,所以大正方形的
面积又可表示成 ab×4+c2. 因此有(a+b)2= ab×4+
c2.整理得a2+b2=c2,即a、b、c为边的直角三角形满足
两直角边的平方和等于斜边的平方.
自主学习
观察如图所示的图形,回答问题:
(1)如图①,△DEF为直角三角形,正方形 P的面积为9,正方形Q的面积为15,则正方形为________;
(2)如图②,分别以直角三角形ABC的三边长为直径向三角形外作三个半圆,则这三个半圆形的面积之间的关系式是________; (用图中字母表示)
(3)如图③,如果直角三角形两直
角边的长分别为3和4,分别以
直角三角形的三边长为直径作
半圆,请你利用(2)中得出的结论求阴影部分的面积.
例2
典例分析
(1)根据正方形的面积公式,结合勾股定理可得
DF2=DE2+EF2,即正方形M的面积=9+15=24;
(2)
另外由勾股定理可知AC2+BC2=AB2,所以S1+S2=S3;
(3)阴影部分的面积=两个小半圆形的面积和+直角三角
形的面积-大半圆形的面积,由(2)可知两个小半圆形
的面积和=大半圆形的面积,所以阴影部分的面积=
直角三角形的面积.
典例分析
(1)24
(2)S1+S2=S3
(3)设两个小半圆形的面积分别为S1,S2,大半圆
形的面积为S3,三角形的面积为S△,
则S阴影=S1+S2+S△-S3
=S△= ×3×4=6.
解:
典例分析
1.
如图,图中所有的三角形都是直角三角形,四边
形都是正方形.已知正方形A,B,C,D的边长分
别是12,16,9,12,求最大正方形E的面积.
SE=(122+162)+(92+122)
=400+225
=625.
解:
课堂练习
勾股定理
1. 勾股定理的适用条件:直角三角形;它反映了直角
三角形三边关系.
2.由勾股定理的基本关系式:a2+b2=c2可得到一些
变形关系式:c2=a2+b2=(a+b)2-2ab=(a-b)2
+2ab;a2=c2-b2=(c+b)(c-b)等.
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1) 已知a=12,b=5,求c;
(2) 已知a=3,c=4,求b;
(3) 已知c=10,b=9,求a.
解:
备选习题
2.一木杆在离地面3 m处折断,木杆顶端落在离木杆底端
4 m处.木杆折断之前有多高?
解:由题意得,图中直角三角形斜边长为 =5 (m),
∴木杆折断之前有3+5=8 (m).
备选习题
3.如图,一个圆锥的高AO=2.4,底面半径OB=0.7. AB的
长是多少?
解:在Rt△ABO中,AO=2.4,OB=0.7,由勾股定理得
AB=
故AB的长为2.5.
备选习题
https://www.21cnjy.com/help/help_extract.php
