第六章 特殊平行四边形专项训练 利用特殊平行四边形的性质巧解动点问题(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形专项训练 利用特殊平行四边形的性质巧解动点问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 14:32:47 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
利用特殊平行四边形的性质巧解动点问题
类型一 菱形中的动点问题
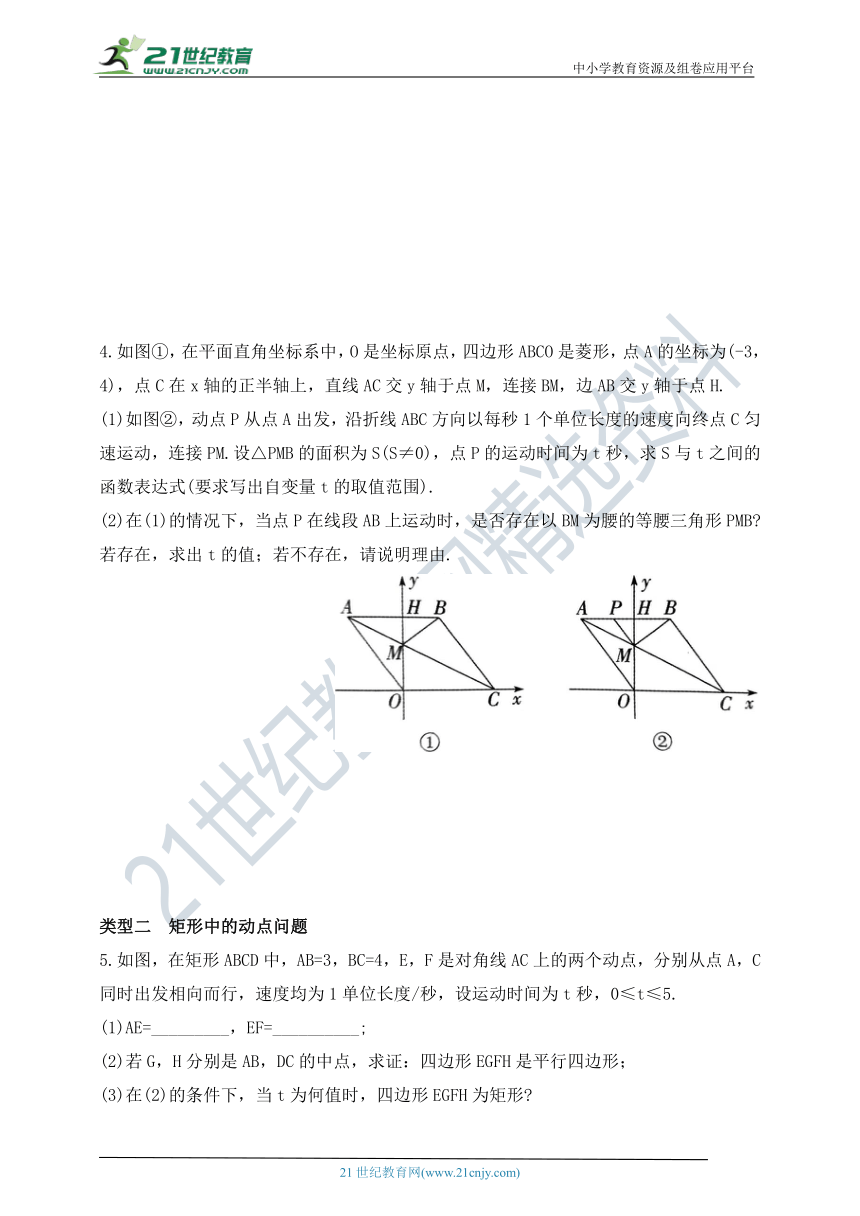
1.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E,PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
2.如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连接DE并延长,交射线AB于点F,连接BE.
(1)求证:∠FFB=∠CBE;
(2)若∠DAB=90°,△BEF为等腰三角形,求∠EFB的度数.
3.如图,在菱形ABCD中,AB=2,∠DAB=60°,E是边AD的中点,M是边AB上的一动点(不与点A重合),连接ME并延长,交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形.
(2)填空:①当AM=_________时,四边形AMDN是矩形.
②当AM=_________时,四边形AMDN是菱形.
③四边形AMDN能为正方形吗 若能,请求出AM的长,并给出证明;若不能,请说明理由.
4.如图①,在平面直角坐标系中,O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,连接BM,边AB交y轴于点H.
(1)如图②,动点P从点A出发,沿折线ABC方向以每秒1个单位长度的速度向终点C匀速运动,连接PM.设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数表达式(要求写出自变量t的取值范围).
(2)在(1)的情况下,当点P在线段AB上运动时,是否存在以BM为腰的等腰三角形PMB 若存在,求出t的值;若不存在,请说明理由.
类型二 矩形中的动点问题
5.如图,在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从点A,C同时出发相向而行,速度均为1单位长度/秒,设运动时间为t秒,0≤t≤5.
(1)AE=_________,EF=__________;
(2)若G,H分别是AB,DC的中点,求证:四边形EGFH是平行四边形;
(3)在(2)的条件下,当t为何值时,四边形EGFH为矩形
6.如图①,在矩形ABCD中,E是边AD上的一个动点,F是边BC上的一个动点,连接EF,把矩形ABCD沿直线EF折叠,点B恰好落在边AD上的点G处.如图②,把矩形展开铺平,连接BE,FG.判断四边形BEGF的形状,并证明你的结论.
类型三 正方形中的动点问题
7.如图,在平面直角坐标系中,D是正方形OABC的边AB上的动点,OC=6.以AD为一边在AB的右侧作正方形ADEF,连接BF.
(1)请直接写出点A,B的坐标.
(2)在点D的运动过程中,OD与BF是否存在特殊的位置关系 若存在,试写出OD与BF的位置关系,并证明;若不存在,请说明理由.
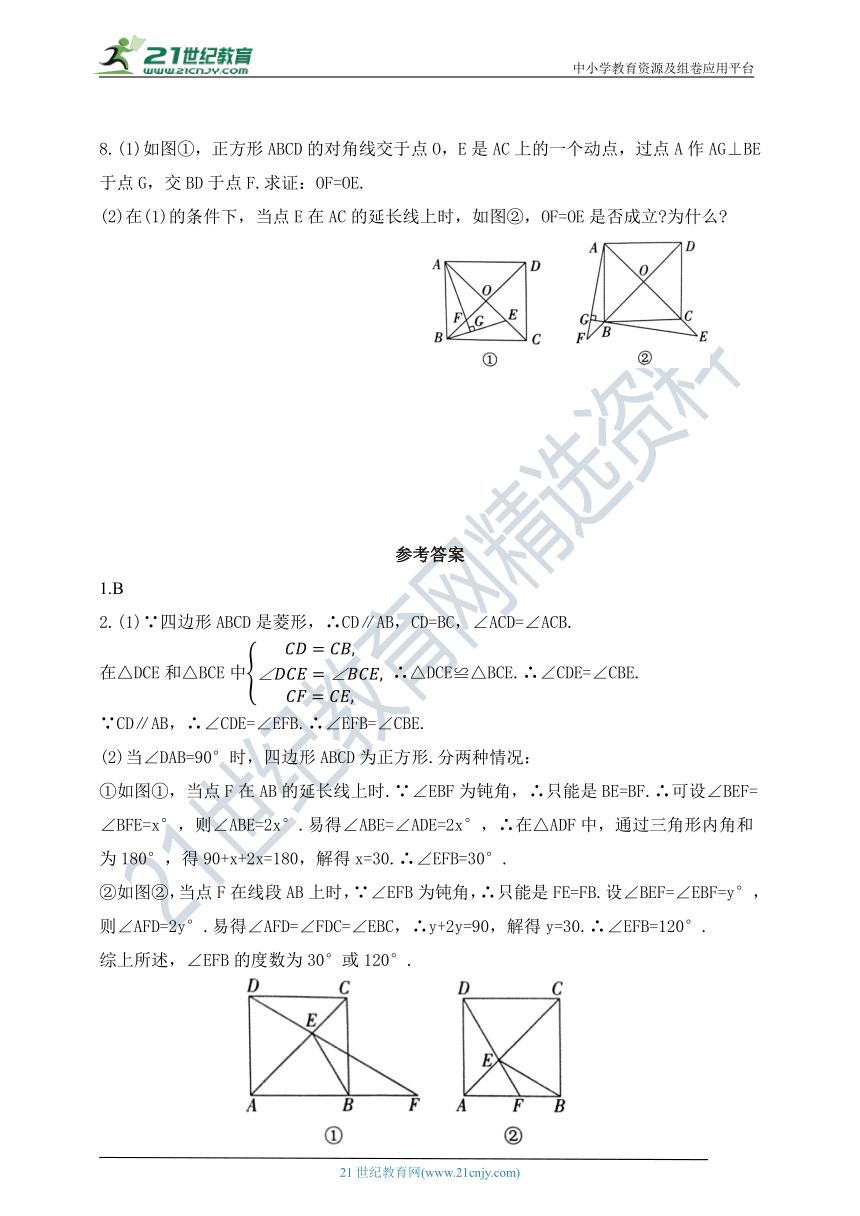
8.(1)如图①,正方形ABCD的对角线交于点O,E是AC上的一个动点,过点A作AG⊥BE于点G,交BD于点F.求证:OF=OE.
(2)在(1)的条件下,当点E在AC的延长线上时,如图②,OF=OE是否成立 为什么
参考答案
1.B
2.(1)∵四边形ABCD是菱形,∴CD∥AB,CD=BC,∠ACD=∠ACB.
在△DCE和△BCE中 ∴△DCE≌△BCE.∴∠CDE=∠CBE.
∵CD∥AB,∴∠CDE=∠EFB.∴∠EFB=∠CBE.
(2)当∠DAB=90°时,四边形ABCD为正方形.分两种情况:
①如图①,当点F在AB的延长线上时.∵∠EBF为钝角,∴只能是BE=BF.∴可设∠BEF=∠BFE=x°,则∠ABE=2x°.易得∠ABE=∠ADE=2x°,∴在△ADF中,通过三角形内角和为180°,得90+x+2x=180,解得x=30.∴∠EFB=30°.
②如图②,当点F在线段AB上时,∵∠EFB为钝角,∴只能是FE=FB.设∠BEF=∠EBF=y°,则∠AFD=2y°.易得∠AFD=∠FDC=∠EBC,∴y+2y=90,解得y=30.∴∠EFB=120°.
综上所述,∠EFB的度数为30°或120°.
3.(1)∵四边形ABCD是菱形,∴ND∥MA.∴∠CNDE=∠MAE,∠DNE=∠AME.∵E是边AD的中点,∴DE=AE.∴△NDE≌△MAE.∴ND=MA.又∵ND∥MA,∴四边形AMDN是平行四边形.
(2) ①1 ②2 ③不能
理由:当四边形AMDN为正方形时,它既是矩形又是菱形,而AM=1,AM=2不能同时满足.∴四边形AMDN不能为正方形.
4.(1)∵点A的坐标为(-3,4),∴∴AB=BC=OC=AO=5.∴点C的坐标为(5,0).设直线AC对应的函数表达式为y=kx+b.将A(-3,4),C(5,0)代入,
易得:∴∴易得点M的坐标为设点M到BC的距离为h.由 得 解得 ①当点P在线段AB上时,S与t之间的函数表达式为 ”,即
②当点P在线段BC上时,S与t之间的函数表达式为 5)×,即 .
(2)存在 ①当MB=MP时,x点A的坐标为(-3,4),AB=5,MB=MP,MH⊥AB,∴PH=BH,即3-t=5-3.∴t=1.
②当BM=BP时,即 解得
综上所述,当t=1或时,△PN是以BM为腰的等腰三角形.
5.(1)t 5-2t或2t-5
(2)∵四边形ABCD是矩形,∴AB=CD,AB∥CD,AD∥BC,∠B=90°.∴AC= /HCE.∵G,H分别是AB,DC的中点,∴ AB D.∴AG=CH.由题意,得AE=CF,∴AF=CE.在△AFG和△CEH中,∴△ .同理可得GE=HF,∴四边形EGFH是平行四边形.
(3)如图,连接GH.由(2),可知四边形EGFH是平行四边形.∵G,H分别是矩形ABCD的边AB,DC的中点,∴易得GH=BC=4.∴当EF=GH=4时,四边形EGFH是矩形.分两种情况:
①0≤t≤2.5时,EF=5-2t=4,解得t=0.5.②2.5<t≤5时,EF=2t-5=4,解得t=4.5.
∴当t的值为0.5或4.5时,四边形EGFH为矩形.
6.四边形BEGF是菱形.
∵四边形ABCD是矩形,∴AD∥BC.∴∠DEF=∠EFB.∵把矩形ABCD沿直线EF折叠,点B恰好落在边AD上的点G处,∴∠EFB=∠EFG,BF=FG.∴∠DEF=∠EFG.∴EG=FG.∴EG=BF.
∵AD∥BC,∴四边形BEGF是平行四边形.又∵BF=FG,∴四边形BEGF是菱形.
7.(1)点A的坐标为(6,0),点B的坐标为(6,6)
(2)存在 OD⊥BF 延长OD交BF于点G.∵四边形OABC和四边形ADEF都是正方形,∴OA=BA,AD=AF,∠BAF=∠OAD=90°.在△AOD和△ABF中,
∴△AOD≌△ABF.∴∠AOD=∠ABF.∵∠ABF+∠AFB=90°,∴∠AOD+∠AFB=90°.∴∠OGF=90°.∴OD⊥BF.
8.(1)∵四边形ABCD为正方形,∴OA=OB,∠AOF=∠BOE=90°.∴∠OBE+∠BEO=90°.∵AG⊥BE,∴∠AGE=90°.∴∠GAE+∠BEO=90°.∴∠GAE=∠OBE.
在△AOF和△BOE中, ∴△AOF≌△BOE.∴OF=OE.
(2)成立 ∵四边形ABCD是正方形,∴AO=BO,∠AOB=∠BOC=90°.
∴∠OBE+∠BEO=90°.∵AG⊥GE,∴∠AGE=90°.∴∠EAG+∠BEO=90°.∴∠EAG=∠OBE.在△AOF和△BOE中,∴△AOF≌△BOE.∴OF=OE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
利用特殊平行四边形的性质巧解动点问题
类型一 菱形中的动点问题
1.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E,PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为( )
A.4 B. C.6 D.
2.如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连接DE并延长,交射线AB于点F,连接BE.
(1)求证:∠FFB=∠CBE;
(2)若∠DAB=90°,△BEF为等腰三角形,求∠EFB的度数.
3.如图,在菱形ABCD中,AB=2,∠DAB=60°,E是边AD的中点,M是边AB上的一动点(不与点A重合),连接ME并延长,交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形.
(2)填空:①当AM=_________时,四边形AMDN是矩形.
②当AM=_________时,四边形AMDN是菱形.
③四边形AMDN能为正方形吗 若能,请求出AM的长,并给出证明;若不能,请说明理由.
4.如图①,在平面直角坐标系中,O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,连接BM,边AB交y轴于点H.
(1)如图②,动点P从点A出发,沿折线ABC方向以每秒1个单位长度的速度向终点C匀速运动,连接PM.设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数表达式(要求写出自变量t的取值范围).
(2)在(1)的情况下,当点P在线段AB上运动时,是否存在以BM为腰的等腰三角形PMB 若存在,求出t的值;若不存在,请说明理由.
类型二 矩形中的动点问题
5.如图,在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从点A,C同时出发相向而行,速度均为1单位长度/秒,设运动时间为t秒,0≤t≤5.
(1)AE=_________,EF=__________;
(2)若G,H分别是AB,DC的中点,求证:四边形EGFH是平行四边形;
(3)在(2)的条件下,当t为何值时,四边形EGFH为矩形
6.如图①,在矩形ABCD中,E是边AD上的一个动点,F是边BC上的一个动点,连接EF,把矩形ABCD沿直线EF折叠,点B恰好落在边AD上的点G处.如图②,把矩形展开铺平,连接BE,FG.判断四边形BEGF的形状,并证明你的结论.
类型三 正方形中的动点问题
7.如图,在平面直角坐标系中,D是正方形OABC的边AB上的动点,OC=6.以AD为一边在AB的右侧作正方形ADEF,连接BF.
(1)请直接写出点A,B的坐标.
(2)在点D的运动过程中,OD与BF是否存在特殊的位置关系 若存在,试写出OD与BF的位置关系,并证明;若不存在,请说明理由.
8.(1)如图①,正方形ABCD的对角线交于点O,E是AC上的一个动点,过点A作AG⊥BE于点G,交BD于点F.求证:OF=OE.
(2)在(1)的条件下,当点E在AC的延长线上时,如图②,OF=OE是否成立 为什么
参考答案
1.B
2.(1)∵四边形ABCD是菱形,∴CD∥AB,CD=BC,∠ACD=∠ACB.
在△DCE和△BCE中 ∴△DCE≌△BCE.∴∠CDE=∠CBE.
∵CD∥AB,∴∠CDE=∠EFB.∴∠EFB=∠CBE.
(2)当∠DAB=90°时,四边形ABCD为正方形.分两种情况:
①如图①,当点F在AB的延长线上时.∵∠EBF为钝角,∴只能是BE=BF.∴可设∠BEF=∠BFE=x°,则∠ABE=2x°.易得∠ABE=∠ADE=2x°,∴在△ADF中,通过三角形内角和为180°,得90+x+2x=180,解得x=30.∴∠EFB=30°.
②如图②,当点F在线段AB上时,∵∠EFB为钝角,∴只能是FE=FB.设∠BEF=∠EBF=y°,则∠AFD=2y°.易得∠AFD=∠FDC=∠EBC,∴y+2y=90,解得y=30.∴∠EFB=120°.
综上所述,∠EFB的度数为30°或120°.
3.(1)∵四边形ABCD是菱形,∴ND∥MA.∴∠CNDE=∠MAE,∠DNE=∠AME.∵E是边AD的中点,∴DE=AE.∴△NDE≌△MAE.∴ND=MA.又∵ND∥MA,∴四边形AMDN是平行四边形.
(2) ①1 ②2 ③不能
理由:当四边形AMDN为正方形时,它既是矩形又是菱形,而AM=1,AM=2不能同时满足.∴四边形AMDN不能为正方形.
4.(1)∵点A的坐标为(-3,4),∴∴AB=BC=OC=AO=5.∴点C的坐标为(5,0).设直线AC对应的函数表达式为y=kx+b.将A(-3,4),C(5,0)代入,
易得:∴∴易得点M的坐标为设点M到BC的距离为h.由 得 解得 ①当点P在线段AB上时,S与t之间的函数表达式为 ”,即
②当点P在线段BC上时,S与t之间的函数表达式为 5)×,即 .
(2)存在 ①当MB=MP时,x点A的坐标为(-3,4),AB=5,MB=MP,MH⊥AB,∴PH=BH,即3-t=5-3.∴t=1.
②当BM=BP时,即 解得
综上所述,当t=1或时,△PN是以BM为腰的等腰三角形.
5.(1)t 5-2t或2t-5
(2)∵四边形ABCD是矩形,∴AB=CD,AB∥CD,AD∥BC,∠B=90°.∴AC= /HCE.∵G,H分别是AB,DC的中点,∴ AB D.∴AG=CH.由题意,得AE=CF,∴AF=CE.在△AFG和△CEH中,∴△ .同理可得GE=HF,∴四边形EGFH是平行四边形.
(3)如图,连接GH.由(2),可知四边形EGFH是平行四边形.∵G,H分别是矩形ABCD的边AB,DC的中点,∴易得GH=BC=4.∴当EF=GH=4时,四边形EGFH是矩形.分两种情况:
①0≤t≤2.5时,EF=5-2t=4,解得t=0.5.②2.5<t≤5时,EF=2t-5=4,解得t=4.5.
∴当t的值为0.5或4.5时,四边形EGFH为矩形.
6.四边形BEGF是菱形.
∵四边形ABCD是矩形,∴AD∥BC.∴∠DEF=∠EFB.∵把矩形ABCD沿直线EF折叠,点B恰好落在边AD上的点G处,∴∠EFB=∠EFG,BF=FG.∴∠DEF=∠EFG.∴EG=FG.∴EG=BF.
∵AD∥BC,∴四边形BEGF是平行四边形.又∵BF=FG,∴四边形BEGF是菱形.
7.(1)点A的坐标为(6,0),点B的坐标为(6,6)
(2)存在 OD⊥BF 延长OD交BF于点G.∵四边形OABC和四边形ADEF都是正方形,∴OA=BA,AD=AF,∠BAF=∠OAD=90°.在△AOD和△ABF中,
∴△AOD≌△ABF.∴∠AOD=∠ABF.∵∠ABF+∠AFB=90°,∴∠AOD+∠AFB=90°.∴∠OGF=90°.∴OD⊥BF.
8.(1)∵四边形ABCD为正方形,∴OA=OB,∠AOF=∠BOE=90°.∴∠OBE+∠BEO=90°.∵AG⊥BE,∴∠AGE=90°.∴∠GAE+∠BEO=90°.∴∠GAE=∠OBE.
在△AOF和△BOE中, ∴△AOF≌△BOE.∴OF=OE.
(2)成立 ∵四边形ABCD是正方形,∴AO=BO,∠AOB=∠BOC=90°.
∴∠OBE+∠BEO=90°.∵AG⊥GE,∴∠AGE=90°.∴∠EAG+∠BEO=90°.∴∠EAG=∠OBE.在△AOF和△BOE中,∴△AOF≌△BOE.∴OF=OE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
