5.1.3同位角、内错角、同旁内角(含答案)【知识清单+经典例题+夯实基础+提优特训+中考链接】
文档属性
| 名称 | 5.1.3同位角、内错角、同旁内角(含答案)【知识清单+经典例题+夯实基础+提优特训+中考链接】 |

|
|
| 格式 | zip | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 10:49:55 | ||
图片预览

文档简介
21世纪教育网 –全国领先的中小学教育资源及组卷应用平台
人教版2021-2022学年度下学期七年级数学下册第5章相交线与平行线
5.1相交线
5.1.3 同位角、内错角、同旁内角
【知识清单】
如图1,两条直线AB,CD被第三条直线EF所截,构成了八个角.分别为∠1,∠2,∠3,∠4,∠5,∠6,∠7,∠8,它们之间有多种位置关系:
1.∠1与∠5的位置,这两个角分别在直线AB,CD的同一方(上方),
并且都在直线EF的同侧(右侧),即具有这种位置关系的一对角叫做同位角.
请你找出其他的同位角 .
2.∠3与∠5的位置,这两个角分别在直线AB,CD之间,并且分别
在直线EF两侧(∠3在直线EF的左侧,∠5在直线EF右侧),具有这种位
置关系的一对角叫做内错角. 请你找出其他的内错角 .
3.∠3与∠6的位置,这两个角分别在直线AB,CD之间,它们在直线EF的同一旁(左侧),具有这种位置关系的一对角叫做同旁内角. 请你找出其他的同旁内角 .
【经典例题】
例题1.下列图形中,∠1与∠2不是同位角的是( )
【考点】同位角、内错角、同旁内角.
【分析】同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
【解答】A图中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,
不符合题意;
B图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角
不符合题意;
C图中,∠1与∠2的两条边都不在同一条直线上,不是同位角,符合题意;
D图中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,
不符合题意.
故选C.
【点评】此题主要考查了同位角、内错角、同旁内角等知识,判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
例题2.如图,用数字标出的八个角中,同位角、内错角、
同旁内角分别有哪些?请把它们一一写出来.
【考点】同位角、内错角、同旁内角.
【分析】根根据两直线被第三条直线所截,所形成的角中,两角在两条直线的中间,第三条直线的两边,可得内错角,根据两角在两直线的中间,第三条直线的同侧,可得同旁内角,两角的位置相同,可得同位角.
【解答】:同位角:∠1与∠7,∠2与∠8,∠4与∠6.
内错角:∠3与∠4,∠1与∠5,∠2与∠6,∠4与∠8;
同旁内角:∠1与∠6,∠2与∠5,∠2与∠4,∠4与∠5;
【点评】本题考查了同位角、内错角,同旁内角,注意同位角、内错角,同旁内角都是相对于角的位置而言.
【夯实基础】
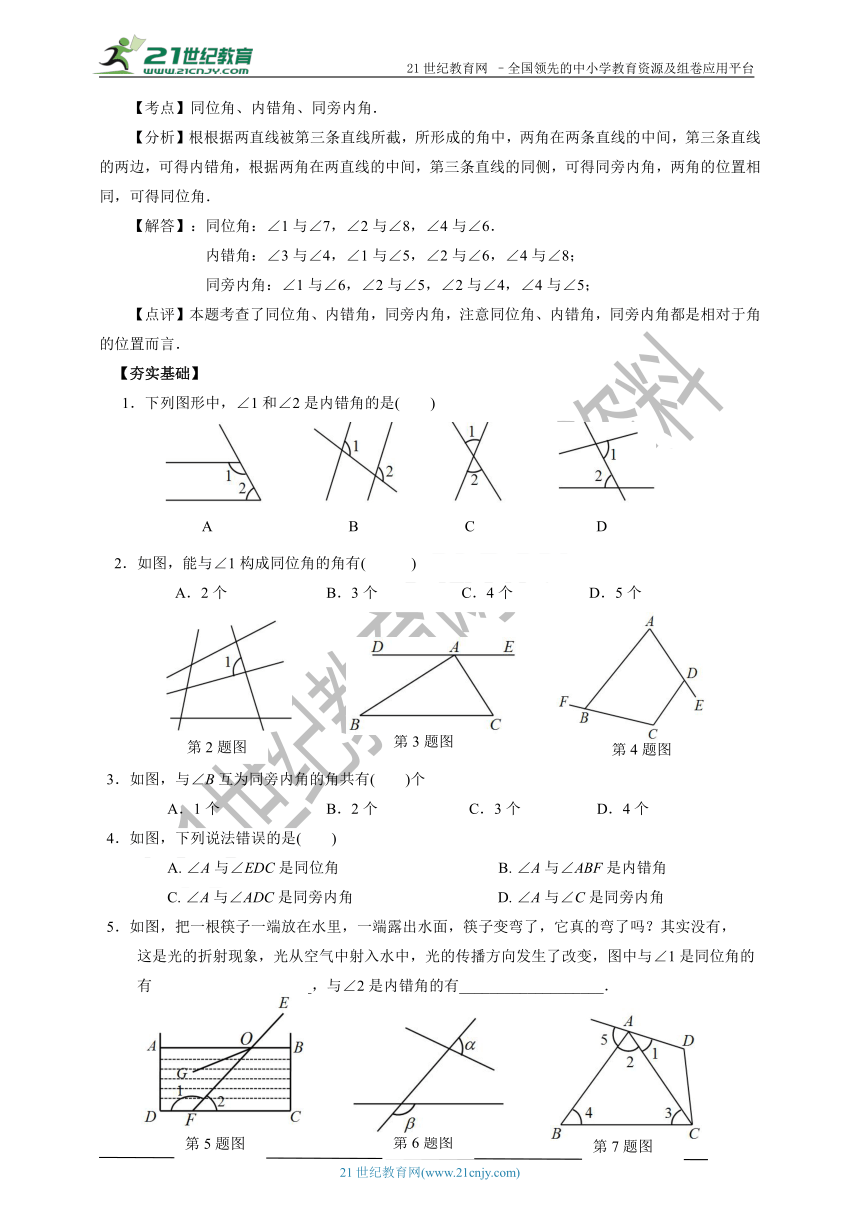
1.下列图形中,∠1和∠2是内错角的是( )
2.如图,能与∠1构成同位角的角有( )
A.2个 B.3个 C.4个 D.5个
3.如图,与∠B互为同旁内角的角共有( )个
A.1个 B.2个 C.3个 D.4个
4.如图,下列说法错误的是( )
A. ∠A与∠EDC是同位角 B. ∠A与∠ABF是内错角
C. ∠A与∠ADC是同旁内角 D. ∠A与∠C是同旁内角
5.如图,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,
这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变,图中与∠1是同位角的
有_____________________,与∠2是内错角的有___________________.
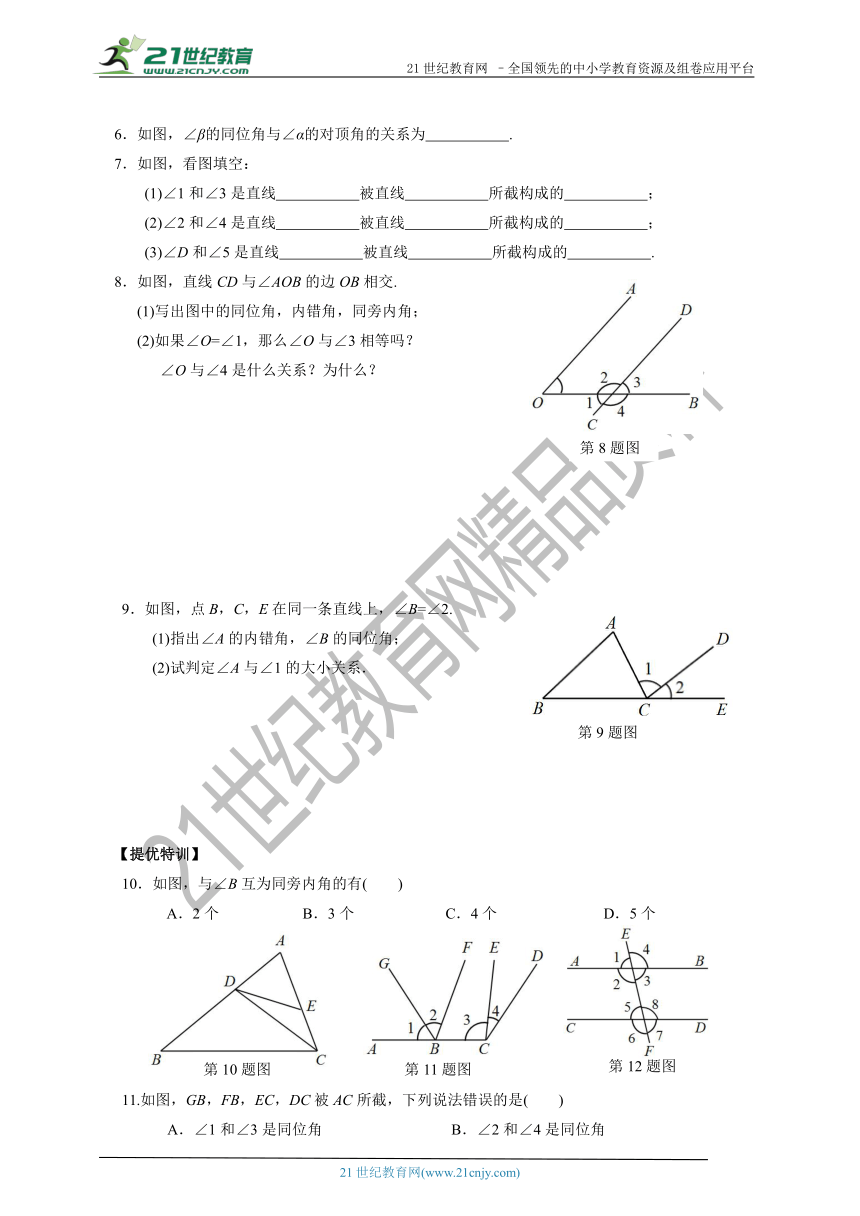
6.如图,∠β的同位角与∠α的对顶角的关系为 .
7.如图,看图填空:
(1)∠1和∠3是直线 被直线 所截构成的 ;
(2)∠2和∠4是直线 被直线 所截构成的 ;
(3)∠D和∠5是直线 被直线 所截构成的 .
8.如图,直线CD与∠AOB的边OB相交.
(1)写出图中的同位角,内错角,同旁内角;
(2)如果∠O=∠1,那么∠O与∠3相等吗?
∠O与∠4是什么关系?为什么?
9.如图,点B,C,E在同一条直线上,∠B=∠2.
(1)指出∠A的内错角,∠B的同位角;
(2)试判定∠A与∠1的大小关系.
【提优特训】
10.如图,与∠B互为同旁内角的有( )
A.2个 B.3个 C.4个 D.5个
11.如图,GB,FB,EC,DC被AC所截,下列说法错误的是( )
A.∠1和∠3是同位角 B.∠2和∠4是同位角
C.∠ABF和∠ACD是同位角 D.∠ABF和∠3是同位角
12.如图所示,两条直线AB,CD被第三条直线EF所截,若∠2+∠5=180°,
则下列结论:①∠1=∠5;②∠3+∠7=180°;③∠4=∠6;④∠2=∠7;
⑤∠4和∠7互补.其中正确的个数为( )
A.5个 B.4个 C.3个 D.2个
13.下列图中,∠A的内错角与∠1的内错角的关系为( )
A.互补 B.相等 C.互余 D.无法确定
14.如图,图中所有标出来的角中与∠5同位角的是 .
15.如图,同位角有a对,内错角有b对,同旁内角有c对,则a+b+c的值是 .
16.如图,直线a、b被直线c所截,∠1=100°,∠3=38°,则∠3的同位角的度数为 ;
∠1内错角的度数为 ;∠2+∠3= °.
17.两条直线l1与l2被第三条直线l3所截,∠1是∠2的内错角,∠2是∠3的同旁内角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠2=4∠1,∠2:∠3=1:2,求∠1,∠2,∠3的度数.
18.如图,已知直线CD分别与AB、EF相交于P、Q,PE平分∠BPD,若∠APC=110°,∠FQD=∠BPC.
(1)求∠BPE的度数;
(2)写出一个与∠EPQ互为同位角的角;
(3)试探究PE与FE的位置关系?.
【中考链接】
19.(2021 桂林) 下面四个图中,∠1=∠2一定成立的是 ( )
20.(2021 贺州) 如图,下列两个角是同旁内角是( )
A.∠1与∠2 B.∠1与∠3 C.∠1与∠4 D.∠2与∠4
参考答案
1.D 2.B 3.C 4.D 5.∠EOG,∠AOE,∠C;∠GOF,∠AOF 6.互为补角
10.D 11.B 12.C 13.A 14.∠1与∠6 15.8 16.80°,142°,118°
19.B 20.B
7.如图,看图填空:
(1)∠1和∠3是直线 AD,BC 被直线 AC 所截构成的 内错角 ;
(2)∠2和∠4是直线 AC,BC 被直线 AB 所截构成的 同旁内角 ;
(3)∠D和∠5是直线 AB,DC 被直线 AD 所截构成的 同位角 .
8.如图,直线CD与∠AOB的边OB相交.
(1)写出图中的同位角,内错角,同旁内角;
(2)如果∠O=∠1,那么∠O与∠3相等吗?
∠O与∠4是什么关系?为什么?
解:(1)如图,同位角是:∠O与∠3,
内错角是:∠O与∠1,
同旁内角是:∠O与∠2;
(2) ∠O=∠3,理由如下:
∵∠O =∠1,∠1 =∠3,
∴∠O=∠3,
∠O与∠4是互补的关系,理由如下:
∵∠O =∠1,
∴∠1+∠2=180°(平角的意义),
∴∠O+∠2=180°.
9.如图,点B,C,E在同一条直线上,∠B=∠2.
(1)指出∠A的内错角,∠B的同位角;
(2)试判定∠A与∠1的大小关系.
解:(1)∠A的内错角:∠1和∠ACE ,
∠B的同位角:∠ACE和∠2;
(2)∵∠BCE是平角,
∴∠ACB+∠1+∠2=180°
∵三角形ABC的内角和为180°,
∴∠A+∠B+∠ACB=180°,
∴∠ACB+∠1+∠2=∠A+∠B+∠ACB,
∴∠1+∠2=∠A+∠B,
∵∠B=∠2
∴∠1=∠A.
17.两条直线l1与l2被第三条直线l3所截,∠1是∠2的内错角,∠2是∠3的同旁内角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠2=4∠1,∠2:∠3=1:2,求∠1,∠2,∠3的度数.
解:(1)如答图所示:
(2)∵∠2=4∠1,∠2:∠3=1:2,,
∴设∠1=x°,则∠2=4x°,∠3=8x°,
∵∠1+∠3=180°,
∴x°+8x° =180°,
解得x=20°,
故∠1=20°,∠2=80°,∠1=160°.
18.如图,已知直线CD分别与AB、EF相交于P、Q,PE平分∠BPD,若∠APC=110°,∠FQD=∠BPC.
(1)求∠BPE的度数;
(2)写出一个与∠EPQ互为同位角的角;
(3)试探究PE与FE的位置关系?.
解:(1)∵∠APC=110°,
∴∠BPD=110°,
∵PE平分∠BPD,
∴∠BPE=∠EPD =∠BPD=×110°=55°;
(2)与∠BPE互为同位角的角是∠DPE;
(3)∵∠APC=110°,
∴∠BPC=180°-110°=70°,
∵∠FQD=∠BPC,
∴∠FQD=35°,
∵∠PQE=∠FQD=35°,
∴∠FQD=35°,
∵三角形PEQ的内角和为180°,
∴∠EPQ+∠PEQ+∠EQP=180°,
∴55°+∠PEQ+35°=180°,
∴∠PEQ=90°,
∴PE⊥FE,
∴PE与FE的位置关系是相互垂直.
第4题图
A
A B C D
第15题图
第18题图
第7题图
第5题图
第2题图
B
D
第6题图
第3题图
图1
第8题图
第18题图
第17题图
第9题图
例题2图
第11题图
第12题图
第13题图
第14题图
第16题图
C
第9题图
第20题图
第10题图
A B C D
第8题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版2021-2022学年度下学期七年级数学下册第5章相交线与平行线
5.1相交线
5.1.3 同位角、内错角、同旁内角
【知识清单】
如图1,两条直线AB,CD被第三条直线EF所截,构成了八个角.分别为∠1,∠2,∠3,∠4,∠5,∠6,∠7,∠8,它们之间有多种位置关系:
1.∠1与∠5的位置,这两个角分别在直线AB,CD的同一方(上方),
并且都在直线EF的同侧(右侧),即具有这种位置关系的一对角叫做同位角.
请你找出其他的同位角 .
2.∠3与∠5的位置,这两个角分别在直线AB,CD之间,并且分别
在直线EF两侧(∠3在直线EF的左侧,∠5在直线EF右侧),具有这种位
置关系的一对角叫做内错角. 请你找出其他的内错角 .
3.∠3与∠6的位置,这两个角分别在直线AB,CD之间,它们在直线EF的同一旁(左侧),具有这种位置关系的一对角叫做同旁内角. 请你找出其他的同旁内角 .
【经典例题】
例题1.下列图形中,∠1与∠2不是同位角的是( )
【考点】同位角、内错角、同旁内角.
【分析】同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
【解答】A图中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,
不符合题意;
B图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角
不符合题意;
C图中,∠1与∠2的两条边都不在同一条直线上,不是同位角,符合题意;
D图中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,
不符合题意.
故选C.
【点评】此题主要考查了同位角、内错角、同旁内角等知识,判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
例题2.如图,用数字标出的八个角中,同位角、内错角、
同旁内角分别有哪些?请把它们一一写出来.
【考点】同位角、内错角、同旁内角.
【分析】根根据两直线被第三条直线所截,所形成的角中,两角在两条直线的中间,第三条直线的两边,可得内错角,根据两角在两直线的中间,第三条直线的同侧,可得同旁内角,两角的位置相同,可得同位角.
【解答】:同位角:∠1与∠7,∠2与∠8,∠4与∠6.
内错角:∠3与∠4,∠1与∠5,∠2与∠6,∠4与∠8;
同旁内角:∠1与∠6,∠2与∠5,∠2与∠4,∠4与∠5;
【点评】本题考查了同位角、内错角,同旁内角,注意同位角、内错角,同旁内角都是相对于角的位置而言.
【夯实基础】
1.下列图形中,∠1和∠2是内错角的是( )
2.如图,能与∠1构成同位角的角有( )
A.2个 B.3个 C.4个 D.5个
3.如图,与∠B互为同旁内角的角共有( )个
A.1个 B.2个 C.3个 D.4个
4.如图,下列说法错误的是( )
A. ∠A与∠EDC是同位角 B. ∠A与∠ABF是内错角
C. ∠A与∠ADC是同旁内角 D. ∠A与∠C是同旁内角
5.如图,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,
这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变,图中与∠1是同位角的
有_____________________,与∠2是内错角的有___________________.
6.如图,∠β的同位角与∠α的对顶角的关系为 .
7.如图,看图填空:
(1)∠1和∠3是直线 被直线 所截构成的 ;
(2)∠2和∠4是直线 被直线 所截构成的 ;
(3)∠D和∠5是直线 被直线 所截构成的 .
8.如图,直线CD与∠AOB的边OB相交.
(1)写出图中的同位角,内错角,同旁内角;
(2)如果∠O=∠1,那么∠O与∠3相等吗?
∠O与∠4是什么关系?为什么?
9.如图,点B,C,E在同一条直线上,∠B=∠2.
(1)指出∠A的内错角,∠B的同位角;
(2)试判定∠A与∠1的大小关系.
【提优特训】
10.如图,与∠B互为同旁内角的有( )
A.2个 B.3个 C.4个 D.5个
11.如图,GB,FB,EC,DC被AC所截,下列说法错误的是( )
A.∠1和∠3是同位角 B.∠2和∠4是同位角
C.∠ABF和∠ACD是同位角 D.∠ABF和∠3是同位角
12.如图所示,两条直线AB,CD被第三条直线EF所截,若∠2+∠5=180°,
则下列结论:①∠1=∠5;②∠3+∠7=180°;③∠4=∠6;④∠2=∠7;
⑤∠4和∠7互补.其中正确的个数为( )
A.5个 B.4个 C.3个 D.2个
13.下列图中,∠A的内错角与∠1的内错角的关系为( )
A.互补 B.相等 C.互余 D.无法确定
14.如图,图中所有标出来的角中与∠5同位角的是 .
15.如图,同位角有a对,内错角有b对,同旁内角有c对,则a+b+c的值是 .
16.如图,直线a、b被直线c所截,∠1=100°,∠3=38°,则∠3的同位角的度数为 ;
∠1内错角的度数为 ;∠2+∠3= °.
17.两条直线l1与l2被第三条直线l3所截,∠1是∠2的内错角,∠2是∠3的同旁内角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠2=4∠1,∠2:∠3=1:2,求∠1,∠2,∠3的度数.
18.如图,已知直线CD分别与AB、EF相交于P、Q,PE平分∠BPD,若∠APC=110°,∠FQD=∠BPC.
(1)求∠BPE的度数;
(2)写出一个与∠EPQ互为同位角的角;
(3)试探究PE与FE的位置关系?.
【中考链接】
19.(2021 桂林) 下面四个图中,∠1=∠2一定成立的是 ( )
20.(2021 贺州) 如图,下列两个角是同旁内角是( )
A.∠1与∠2 B.∠1与∠3 C.∠1与∠4 D.∠2与∠4
参考答案
1.D 2.B 3.C 4.D 5.∠EOG,∠AOE,∠C;∠GOF,∠AOF 6.互为补角
10.D 11.B 12.C 13.A 14.∠1与∠6 15.8 16.80°,142°,118°
19.B 20.B
7.如图,看图填空:
(1)∠1和∠3是直线 AD,BC 被直线 AC 所截构成的 内错角 ;
(2)∠2和∠4是直线 AC,BC 被直线 AB 所截构成的 同旁内角 ;
(3)∠D和∠5是直线 AB,DC 被直线 AD 所截构成的 同位角 .
8.如图,直线CD与∠AOB的边OB相交.
(1)写出图中的同位角,内错角,同旁内角;
(2)如果∠O=∠1,那么∠O与∠3相等吗?
∠O与∠4是什么关系?为什么?
解:(1)如图,同位角是:∠O与∠3,
内错角是:∠O与∠1,
同旁内角是:∠O与∠2;
(2) ∠O=∠3,理由如下:
∵∠O =∠1,∠1 =∠3,
∴∠O=∠3,
∠O与∠4是互补的关系,理由如下:
∵∠O =∠1,
∴∠1+∠2=180°(平角的意义),
∴∠O+∠2=180°.
9.如图,点B,C,E在同一条直线上,∠B=∠2.
(1)指出∠A的内错角,∠B的同位角;
(2)试判定∠A与∠1的大小关系.
解:(1)∠A的内错角:∠1和∠ACE ,
∠B的同位角:∠ACE和∠2;
(2)∵∠BCE是平角,
∴∠ACB+∠1+∠2=180°
∵三角形ABC的内角和为180°,
∴∠A+∠B+∠ACB=180°,
∴∠ACB+∠1+∠2=∠A+∠B+∠ACB,
∴∠1+∠2=∠A+∠B,
∵∠B=∠2
∴∠1=∠A.
17.两条直线l1与l2被第三条直线l3所截,∠1是∠2的内错角,∠2是∠3的同旁内角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠2=4∠1,∠2:∠3=1:2,求∠1,∠2,∠3的度数.
解:(1)如答图所示:
(2)∵∠2=4∠1,∠2:∠3=1:2,,
∴设∠1=x°,则∠2=4x°,∠3=8x°,
∵∠1+∠3=180°,
∴x°+8x° =180°,
解得x=20°,
故∠1=20°,∠2=80°,∠1=160°.
18.如图,已知直线CD分别与AB、EF相交于P、Q,PE平分∠BPD,若∠APC=110°,∠FQD=∠BPC.
(1)求∠BPE的度数;
(2)写出一个与∠EPQ互为同位角的角;
(3)试探究PE与FE的位置关系?.
解:(1)∵∠APC=110°,
∴∠BPD=110°,
∵PE平分∠BPD,
∴∠BPE=∠EPD =∠BPD=×110°=55°;
(2)与∠BPE互为同位角的角是∠DPE;
(3)∵∠APC=110°,
∴∠BPC=180°-110°=70°,
∵∠FQD=∠BPC,
∴∠FQD=35°,
∵∠PQE=∠FQD=35°,
∴∠FQD=35°,
∵三角形PEQ的内角和为180°,
∴∠EPQ+∠PEQ+∠EQP=180°,
∴55°+∠PEQ+35°=180°,
∴∠PEQ=90°,
∴PE⊥FE,
∴PE与FE的位置关系是相互垂直.
第4题图
A
A B C D
第15题图
第18题图
第7题图
第5题图
第2题图
B
D
第6题图
第3题图
图1
第8题图
第18题图
第17题图
第9题图
例题2图
第11题图
第12题图
第13题图
第14题图
第16题图
C
第9题图
第20题图
第10题图
A B C D
第8题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
