2021-2022学年人教版数学八年级下册19.2.2一次函数同步习题 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册19.2.2一次函数同步习题 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 126.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 11:08:43 | ||
图片预览




文档简介
人教版数学八年级下册第十九章19.2.2一次函数
一、选择题
下列函数中,是一次函数的是
A. B. C. D.
下列函数关系式:,其中是一次函数的是
A. B. C. D.
在平面直角坐标系中,已知函数的图象经过点,则该函数的图象可能是
A. B. C. D.
已知一次函数,当时,,且它的图象与轴交点的纵坐标是,那么该函数的解析式为
A. B. C. D.
若一次函数的图象与直线平行,且过点,则此一次函数的解析式为
A. B. C. D.
下列函数中,随的增大而增大的是
A. B. C. D.
若点在一次函数的图象上,则点一定不在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
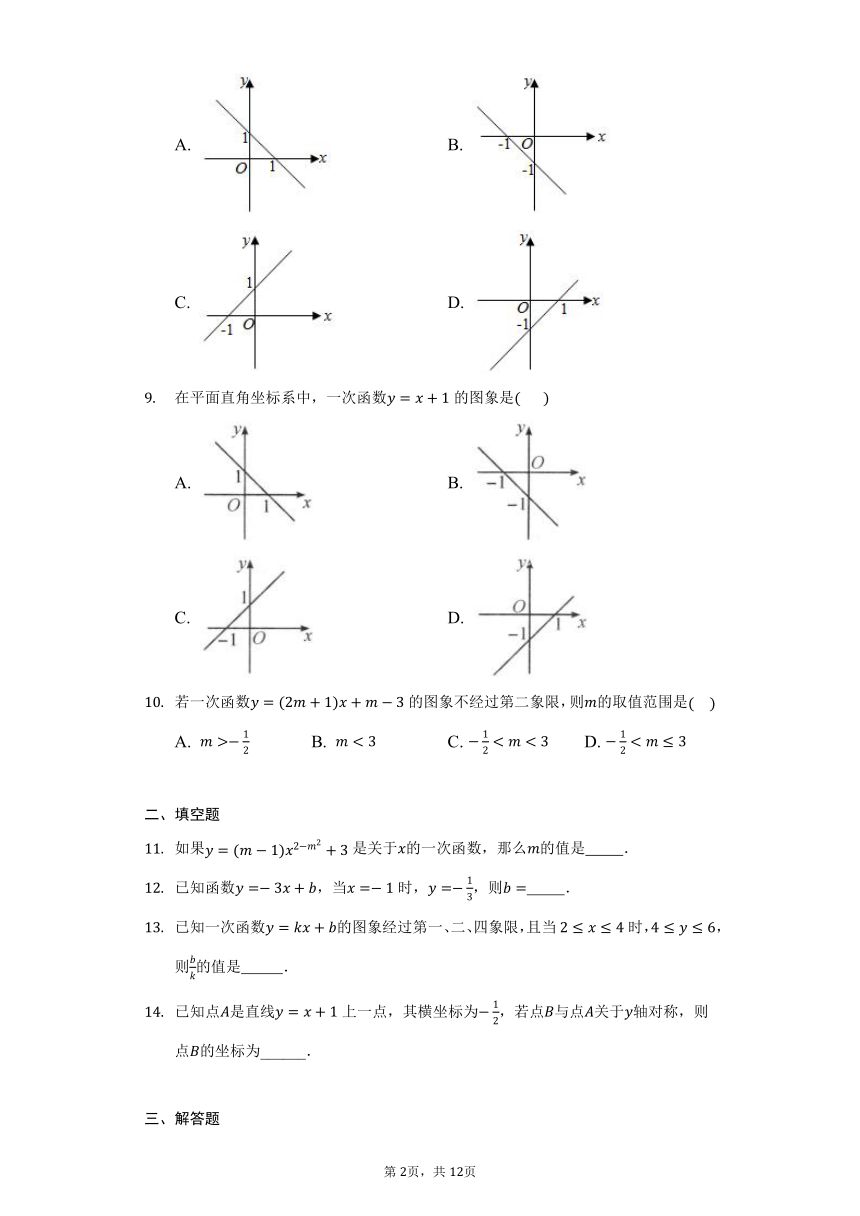
在平面直角坐标系中,一次函数的图象是
A. B.
C. D.
在平面直角坐标系中,一次函数的图象是
A. B.
C. D.
若一次函数的图象不经过第二象限,则的取值范围是
A. B. C. D.
二、填空题
如果是关于的一次函数,那么的值是 .
已知函数,当时,,则 .
已知一次函数的图象经过第一、二、四象限,且当时,,则的值是 .
已知点是直线上一点,其横坐标为,若点与点关于轴对称,则点的坐标为______.
三、解答题
对于老师给定的一次函数,有以下三条关于该函数图象与性质的正确信息:
函数图象与轴交于点
函数图象与轴交于点,且
的值随着值的增大而增大.
根据以上信息画出这个函数的图象,并求出这个函数的解析式.
已知关于的函数.
当,为何值时,它是一次函数?
当,为何值时,它是正比例函数?
如图所示,在平面直角坐标系中,直线过点,,且与轴、轴分别交于点,.
求直线所对应的函数解析式
求的面积.
已知与成正比例,且当时,.
求与之间的函数解析式
当时,求的值.
点在第一象限,且,点的坐标为,设的面积为.
用含的解析式表示,写出的取值范围,画出函数的图象;
当点的横坐标为时,的面积为多少?
的面积能大于吗?为什么?
答案和解析
1.【答案】
【解析】解:中未知数的最高次数为,故本选项错误;
B.中自变量在分母中,不是一次函数,故本选项错误;
C.中未知数的最高次数为,不是一次函数,故本选项错误;
D.是一次函数,故本选项正确.
故选D
2.【答案】
【解析】是一次函数
中自变量在分母上,故不是一次函数
中自变量的次数不为,故不是一次函数
不是一次函数
是一次函数.
所以是一次函数故选A.
3.【答案】
【解析】解:函数的图象过点,
,解得,
,
直线交轴的正半轴于点,且过点,
故选:.
4.【答案】
【解析】解: 一次函数,它的图象与轴交点的纵坐标是,
,
当时,,
,
,
该函数的解析式为,
故选C.
5.【答案】
【解析】解:一次函数的图象与直线平行,
,
一次函数过点,
解得,
一次函数解析式为.
故选D.
6.【答案】
【解析】
【分析】
根据一次函数的性质对各选项进行逐一分析即可.
本题考查的是一次函数的性质,熟知一次函数中,当时随的增大而增大是解答此题的关键.
【解答】
解:、中,随的增大而减小,故本选项错误;
B、中,随的增大而减小,故本选项错误;
C、中,随的增大而增大,故本选项正确;
D、中,随的增大而减小,故本选项错误.
故选:.
7.【答案】
【解析】解:,,
一次函数的图象经过第一、二、四象限,即不经过第三象限.
点在一次函数的图象上,
点一定不在第三象限.
故选:.
结合一次函数图象与系数的关系即可得出一次函数的图象经过第一、二、四象限,此题得解.
本题考查了一次函数图象与系数的关系.
8.【答案】
【解析】解:一次函数中,令,则;令,则,
一次函数的图象经过点和,
一次函数的图象经过一二三象限,
故选:.
9.【答案】
【解析】略
10.【答案】
【解析】解:根据题意得,
解得.
故选:.
11.【答案】
【解析】解:是关于的一次函数,
,,
.
12.【答案】
【解析】解:把,代入,
可得:,
解得:,
故答案为:.
13.【答案】
【解析】解: 一次函数的图象经过第一、二、四象限,
,随的增大而减小.
当时,,
当时,当时,,
解得
.
14解:由题意,
、关于轴对称,
,
故答案为
利用待定系数法求出点坐标,再利用轴对称的性质求出点坐标即可;
本题考查一次函数的应用、轴对称的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
15.【答案】解:点,
,
又,
,
,
函数的图象如图所示:
把点和点的坐标代入,可得
解得
这个函数的表达式为.
【解析】本题主要考查了待定系数法求一次函数解析式,求正比例函数,只要一对,的值就可以,因为它只有一个待定系数;而求一次函数,则需要两组,的值.
依据点和点的坐标,画出函数图象,运用待定系数法即可得到一次函数解析式.
16.【答案】解:当时,,,
故,为任意实数,它是一次函数;
当时,,,,
故,时,它是正比例函数.
【解析】直接利用一次函数的定义进而得出,以及求出即可;
直接利用正比例函数的定义进而得出,以及,求出即可.
此题主要考查了一次函数以及正比例函数的定义,正确把握相关定义是解题关键.
17.【答案】解:设直线的函数关系式为,
把,代入得,
解方程组得:,
直线的函数关系式为;
当时,,,
当,,
解得,
,
.
【解析】本题主要考查用待定系数法求一次函数的解析式.
把两点坐标代入函数解析式得到关于、的二元一次方程组并求解即可得到函数解析式;
求出直线与坐标轴的交点,代入三角形面积公式即可.
18.【答案】解:设,
把,代入,
得,
解得.
则与之间的函数解析式是,
即.
当时,,
解得.
【解析】本题主要考查了待定系数法求函数解析式,解答的关键是正确设出函数的表达式.
可设与之间的函数解析式为,然后将,代入解析式可得的值,然后可得函数解析式;
将代入中的函数解析式可得的值.
19.【答案】解:和点的坐标分别是、,
的面积,
.
,
.
;
,
解得:;
又点在第一象限,
,
即的范围为:;
,是的一次函数,
函数图象经过点,.
所画图象如下:
,
当时,.
即当点的横坐标为时,的面积为;
的面积不能大于理由如下:
,,
随的增大而减小,
又时,,
当,.
即的面积不能大于.
【解析】此题考查了一次函数的图象与性质及三角形的面积,难度一般,解答本题的关键是正确地求出与的关系,另外作图的时候要运用两点作图法,并且注意自变量的取值范围.
根据三角形的面积公式列式,即可用含的解析式表示,然后根据及已知条件,可求出的取值范围,根据一次函数的性质可画出函数的图象;
将代入中所求解析式,即可求出的面积;
根据一次函数的性质及自变量的取值范围即可判断.
第2页,共3页
第1页,共1页
一、选择题
下列函数中,是一次函数的是
A. B. C. D.
下列函数关系式:,其中是一次函数的是
A. B. C. D.
在平面直角坐标系中,已知函数的图象经过点,则该函数的图象可能是
A. B. C. D.
已知一次函数,当时,,且它的图象与轴交点的纵坐标是,那么该函数的解析式为
A. B. C. D.
若一次函数的图象与直线平行,且过点,则此一次函数的解析式为
A. B. C. D.
下列函数中,随的增大而增大的是
A. B. C. D.
若点在一次函数的图象上,则点一定不在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
在平面直角坐标系中,一次函数的图象是
A. B.
C. D.
在平面直角坐标系中,一次函数的图象是
A. B.
C. D.
若一次函数的图象不经过第二象限,则的取值范围是
A. B. C. D.
二、填空题
如果是关于的一次函数,那么的值是 .
已知函数,当时,,则 .
已知一次函数的图象经过第一、二、四象限,且当时,,则的值是 .
已知点是直线上一点,其横坐标为,若点与点关于轴对称,则点的坐标为______.
三、解答题
对于老师给定的一次函数,有以下三条关于该函数图象与性质的正确信息:
函数图象与轴交于点
函数图象与轴交于点,且
的值随着值的增大而增大.
根据以上信息画出这个函数的图象,并求出这个函数的解析式.
已知关于的函数.
当,为何值时,它是一次函数?
当,为何值时,它是正比例函数?
如图所示,在平面直角坐标系中,直线过点,,且与轴、轴分别交于点,.
求直线所对应的函数解析式
求的面积.
已知与成正比例,且当时,.
求与之间的函数解析式
当时,求的值.
点在第一象限,且,点的坐标为,设的面积为.
用含的解析式表示,写出的取值范围,画出函数的图象;
当点的横坐标为时,的面积为多少?
的面积能大于吗?为什么?
答案和解析
1.【答案】
【解析】解:中未知数的最高次数为,故本选项错误;
B.中自变量在分母中,不是一次函数,故本选项错误;
C.中未知数的最高次数为,不是一次函数,故本选项错误;
D.是一次函数,故本选项正确.
故选D
2.【答案】
【解析】是一次函数
中自变量在分母上,故不是一次函数
中自变量的次数不为,故不是一次函数
不是一次函数
是一次函数.
所以是一次函数故选A.
3.【答案】
【解析】解:函数的图象过点,
,解得,
,
直线交轴的正半轴于点,且过点,
故选:.
4.【答案】
【解析】解: 一次函数,它的图象与轴交点的纵坐标是,
,
当时,,
,
,
该函数的解析式为,
故选C.
5.【答案】
【解析】解:一次函数的图象与直线平行,
,
一次函数过点,
解得,
一次函数解析式为.
故选D.
6.【答案】
【解析】
【分析】
根据一次函数的性质对各选项进行逐一分析即可.
本题考查的是一次函数的性质,熟知一次函数中,当时随的增大而增大是解答此题的关键.
【解答】
解:、中,随的增大而减小,故本选项错误;
B、中,随的增大而减小,故本选项错误;
C、中,随的增大而增大,故本选项正确;
D、中,随的增大而减小,故本选项错误.
故选:.
7.【答案】
【解析】解:,,
一次函数的图象经过第一、二、四象限,即不经过第三象限.
点在一次函数的图象上,
点一定不在第三象限.
故选:.
结合一次函数图象与系数的关系即可得出一次函数的图象经过第一、二、四象限,此题得解.
本题考查了一次函数图象与系数的关系.
8.【答案】
【解析】解:一次函数中,令,则;令,则,
一次函数的图象经过点和,
一次函数的图象经过一二三象限,
故选:.
9.【答案】
【解析】略
10.【答案】
【解析】解:根据题意得,
解得.
故选:.
11.【答案】
【解析】解:是关于的一次函数,
,,
.
12.【答案】
【解析】解:把,代入,
可得:,
解得:,
故答案为:.
13.【答案】
【解析】解: 一次函数的图象经过第一、二、四象限,
,随的增大而减小.
当时,,
当时,当时,,
解得
.
14解:由题意,
、关于轴对称,
,
故答案为
利用待定系数法求出点坐标,再利用轴对称的性质求出点坐标即可;
本题考查一次函数的应用、轴对称的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
15.【答案】解:点,
,
又,
,
,
函数的图象如图所示:
把点和点的坐标代入,可得
解得
这个函数的表达式为.
【解析】本题主要考查了待定系数法求一次函数解析式,求正比例函数,只要一对,的值就可以,因为它只有一个待定系数;而求一次函数,则需要两组,的值.
依据点和点的坐标,画出函数图象,运用待定系数法即可得到一次函数解析式.
16.【答案】解:当时,,,
故,为任意实数,它是一次函数;
当时,,,,
故,时,它是正比例函数.
【解析】直接利用一次函数的定义进而得出,以及求出即可;
直接利用正比例函数的定义进而得出,以及,求出即可.
此题主要考查了一次函数以及正比例函数的定义,正确把握相关定义是解题关键.
17.【答案】解:设直线的函数关系式为,
把,代入得,
解方程组得:,
直线的函数关系式为;
当时,,,
当,,
解得,
,
.
【解析】本题主要考查用待定系数法求一次函数的解析式.
把两点坐标代入函数解析式得到关于、的二元一次方程组并求解即可得到函数解析式;
求出直线与坐标轴的交点,代入三角形面积公式即可.
18.【答案】解:设,
把,代入,
得,
解得.
则与之间的函数解析式是,
即.
当时,,
解得.
【解析】本题主要考查了待定系数法求函数解析式,解答的关键是正确设出函数的表达式.
可设与之间的函数解析式为,然后将,代入解析式可得的值,然后可得函数解析式;
将代入中的函数解析式可得的值.
19.【答案】解:和点的坐标分别是、,
的面积,
.
,
.
;
,
解得:;
又点在第一象限,
,
即的范围为:;
,是的一次函数,
函数图象经过点,.
所画图象如下:
,
当时,.
即当点的横坐标为时,的面积为;
的面积不能大于理由如下:
,,
随的增大而减小,
又时,,
当,.
即的面积不能大于.
【解析】此题考查了一次函数的图象与性质及三角形的面积,难度一般,解答本题的关键是正确地求出与的关系,另外作图的时候要运用两点作图法,并且注意自变量的取值范围.
根据三角形的面积公式列式,即可用含的解析式表示,然后根据及已知条件,可求出的取值范围,根据一次函数的性质可画出函数的图象;
将代入中所求解析式,即可求出的面积;
根据一次函数的性质及自变量的取值范围即可判断.
第2页,共3页
第1页,共1页
