1.4.1有理数的乘法
图片预览






文档简介
课件19张PPT。活动一、创设情境, 探究新知 1. 口算下面的乘法.9630当前一个乘数3确定,随着后一乘数逐次递减1,所得的积逐次递减3.观察上面的乘法算式,你能发现什么规律?2.如果这个规律在引入负数后仍然成立,请利用上面的规律,接着计算下面一组题.
-3-6-93.口算下面的算式.
9630当后一个乘数3确定,随着前一乘数逐次递减1,所得的积逐次递减3.观察上面的乘法算式,你又能发现什么规律?-3-6-94.如果这个规律在引入负数后仍然成立,请利用上面的规律,接着计算下面一组题.
9630-3-6-99630-3-6-95.观察以上得到的四组算式. 正数乘正数积为( )数
负数乘正数积为( )数
正数乘负数积为( )数正负负乘积的绝对值等于各乘数
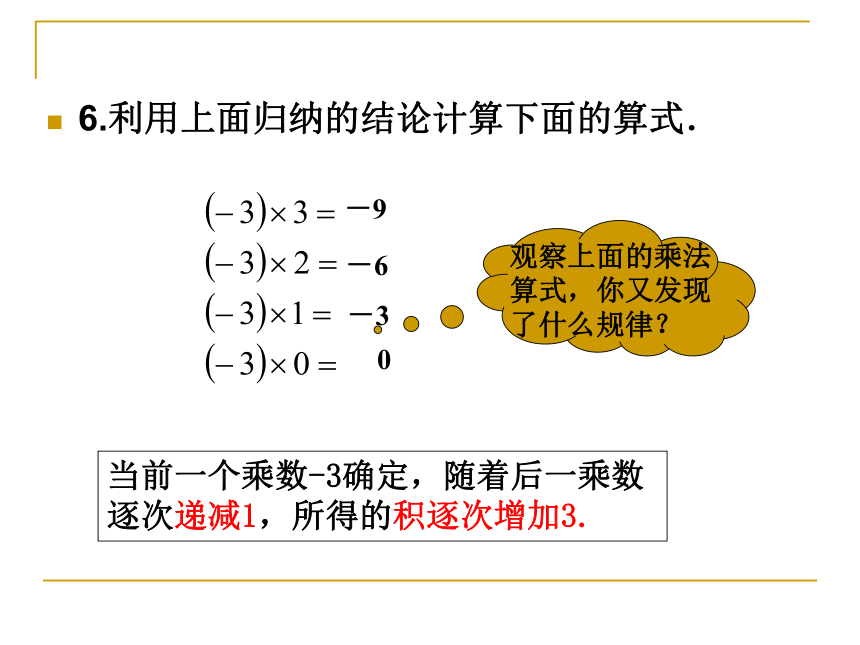
绝对值的( )积从算式左右各数的符号和绝对值两个角度观察,你能发现什么规律?6.利用上面归纳的结论计算下面的算式.-9-6-3 0当前一个乘数-3确定,随着后一乘数逐次递减1,所得的积逐次增加3.观察上面的乘法算式,你又发现了什么规律?369正积负数乘负数,积为( ),
乘积的绝对值等于各乘数绝对值的( ).7.如果上述规律仍然成立,请利用上面的规律,接着计算下面一组题.
思考:当负数与负数相乘时,积的符号是什么?积的绝对值又有什么规律?活动二、深入思考 , 总结法则 两数相乘,同号得正,异号得负,
并把绝对值相乘.
任何数同0相乘,都得0.,………………同号两数相乘
…… 得正
, ………………把绝对值相乘
=所以例如活动三、应用新知, 形成技能例1 计算:
解:思考:有理数乘法的步骤是什么?先分类
同号?
异号?确定符号确定绝对值例2 计算:
解:乘积是1的两个数互为倒数请你写出五组倒数,并与同伴交流例3 明辨是非
老师讲完有理数的乘法后,出了一道检测题,
,同学们的计算结果却不相同,聪明
的你,一定能帮老师找出正确结果!例4 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1 km气温的变化量为-6 ℃,攀登3 km后,气温有什么变化? 解:
答:气温下降 18 ℃.练习一 填写下表:
活动四、巩固法则,提高技能 开始抢答 练习二 计算:练习三 实际应用
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?练习四 趣味数学
在整数-5、-3、-1、0、2、6中,任取两个数相乘,所得积的最大值是多少?活动五、归纳小结, 回顾反思1.本节课你学会了哪些知识?
有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
有理数乘法的运算步骤:一分类;二定符号;三定绝对值.
2.本节课你学到了什么思想方法 ?
转化:有理数乘法确定符号后转化成小学乘法;带分数转化成假分数.
3.你最大的收获是什么? 必做题:教科书P37~38习题1.4 第1、2、3题.
思考题:
1.在整数-5、-3、-1、0、2、6中,任取三个数相乘,所得积的最小值是多少?
2.当ab>0时,判断a、b的符号;当ab<0时,判断a、b的符号.
3.自编一道能用有理数乘法来解决的实际问题.活动六、布置作业 ,巩固知识
-3-6-93.口算下面的算式.
9630当后一个乘数3确定,随着前一乘数逐次递减1,所得的积逐次递减3.观察上面的乘法算式,你又能发现什么规律?-3-6-94.如果这个规律在引入负数后仍然成立,请利用上面的规律,接着计算下面一组题.
9630-3-6-99630-3-6-95.观察以上得到的四组算式. 正数乘正数积为( )数
负数乘正数积为( )数
正数乘负数积为( )数正负负乘积的绝对值等于各乘数
绝对值的( )积从算式左右各数的符号和绝对值两个角度观察,你能发现什么规律?6.利用上面归纳的结论计算下面的算式.-9-6-3 0当前一个乘数-3确定,随着后一乘数逐次递减1,所得的积逐次增加3.观察上面的乘法算式,你又发现了什么规律?369正积负数乘负数,积为( ),
乘积的绝对值等于各乘数绝对值的( ).7.如果上述规律仍然成立,请利用上面的规律,接着计算下面一组题.
思考:当负数与负数相乘时,积的符号是什么?积的绝对值又有什么规律?活动二、深入思考 , 总结法则 两数相乘,同号得正,异号得负,
并把绝对值相乘.
任何数同0相乘,都得0.,………………同号两数相乘
…… 得正
, ………………把绝对值相乘
=所以例如活动三、应用新知, 形成技能例1 计算:
解:思考:有理数乘法的步骤是什么?先分类
同号?
异号?确定符号确定绝对值例2 计算:
解:乘积是1的两个数互为倒数请你写出五组倒数,并与同伴交流例3 明辨是非
老师讲完有理数的乘法后,出了一道检测题,
,同学们的计算结果却不相同,聪明
的你,一定能帮老师找出正确结果!例4 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1 km气温的变化量为-6 ℃,攀登3 km后,气温有什么变化? 解:
答:气温下降 18 ℃.练习一 填写下表:
活动四、巩固法则,提高技能 开始抢答 练习二 计算:练习三 实际应用
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?练习四 趣味数学
在整数-5、-3、-1、0、2、6中,任取两个数相乘,所得积的最大值是多少?活动五、归纳小结, 回顾反思1.本节课你学会了哪些知识?
有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
有理数乘法的运算步骤:一分类;二定符号;三定绝对值.
2.本节课你学到了什么思想方法 ?
转化:有理数乘法确定符号后转化成小学乘法;带分数转化成假分数.
3.你最大的收获是什么? 必做题:教科书P37~38习题1.4 第1、2、3题.
思考题:
1.在整数-5、-3、-1、0、2、6中,任取三个数相乘,所得积的最小值是多少?
2.当ab>0时,判断a、b的符号;当ab<0时,判断a、b的符号.
3.自编一道能用有理数乘法来解决的实际问题.活动六、布置作业 ,巩固知识
