江西省赣州市2022届高三上学期期末考试数学(文)试题(Word版含答案)
文档属性
| 名称 | 江西省赣州市2022届高三上学期期末考试数学(文)试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 791.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 16:44:03 | ||
图片预览




文档简介
赣州市2021-2022学年度第一学期期末考试
高三数学(文科)试卷
2022年1月
第I卷 (选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数(为虚数单位)的共轭复数为
A. B. C. D.
2.已知集合,,则
A. B. C. D.
3.某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行001,002,…,599,600.从中抽取60个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第6个样本编号是
A.457 B.328 C.253 D.072
4.已知等比数列的各项均为正数,且,则
A.6 B.9 C.27 D.81
5.已知双曲线的一条渐近线方程为,且与椭圆有公共焦点,则双曲线的标准方程为
A. B. C. D.
6.已知实数满足,则直线与圆有公共点的概率为
A. B. C. D.
7.若,则
A. B. C. D.
8.已知函数的图像恒过的定点,且点在直线上,则的最小值为
A.4 B.3 C.2 D.1
9.铸于明嘉靖十二年的泰山岱庙铁塔,造型质朴雄伟,原有十三级,抗日战争中被日军飞机炸毁,现仅存三级,它的底座近似圆形(如图1).我国古代工匠已经知道,将长方体砖块以某个固定的角度相接就可砌出近似圆形的建筑,现存铁塔的底座是用10块一样的长方体砖块砌成的近似圆形的墙面,每块长方体砖块底面较长的边长为1个单位,相邻两块砖之间的夹角固定为36°,如图2,则此近似圆形墙面内部所能容纳最大圆的半径是
A. B. C. D.
10.在下列五个命题中,其中正确的个数为
①命题“,都有”的否定为“,有”;
②已知,,若与夹角为锐角,则的取值范围是;
③“”成立的一个充分不必要条件是“”;
④已知是一条直线,,是两个不同的平面,若,,则.
⑤函数的图像向左平移个单位后所得函数解析式为.
A.4 B.3 C.2 D.1
11.已知正方体的棱长为6,则过,,三点的平面与该正方体内切球截面的面积为
A.3π B.6π C.9π D.12π
2.已知是定义在上的奇函数,且当时,都有不等式成立,若,,,则a,b,c的大小关系是
A. B. C. D.
第Ⅱ卷 (非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分.)
13.已知向量,,若,则____________.
14.设曲线在点处的切线与曲线在点P处的切线互相平行,则点P的坐标为___________.
15.抛物线:的焦点为F,点A,B,C在E上,O是坐标原点,若点F为的重心,,,的面积分别为,,.则___________.
16.已知a,b,c分别为的三个内角A,B,C的对边,,且,O是内一点,且满足为,,则___________.
三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤。第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答)
(一)必考题(共60分)
17.(本小题满分12分)
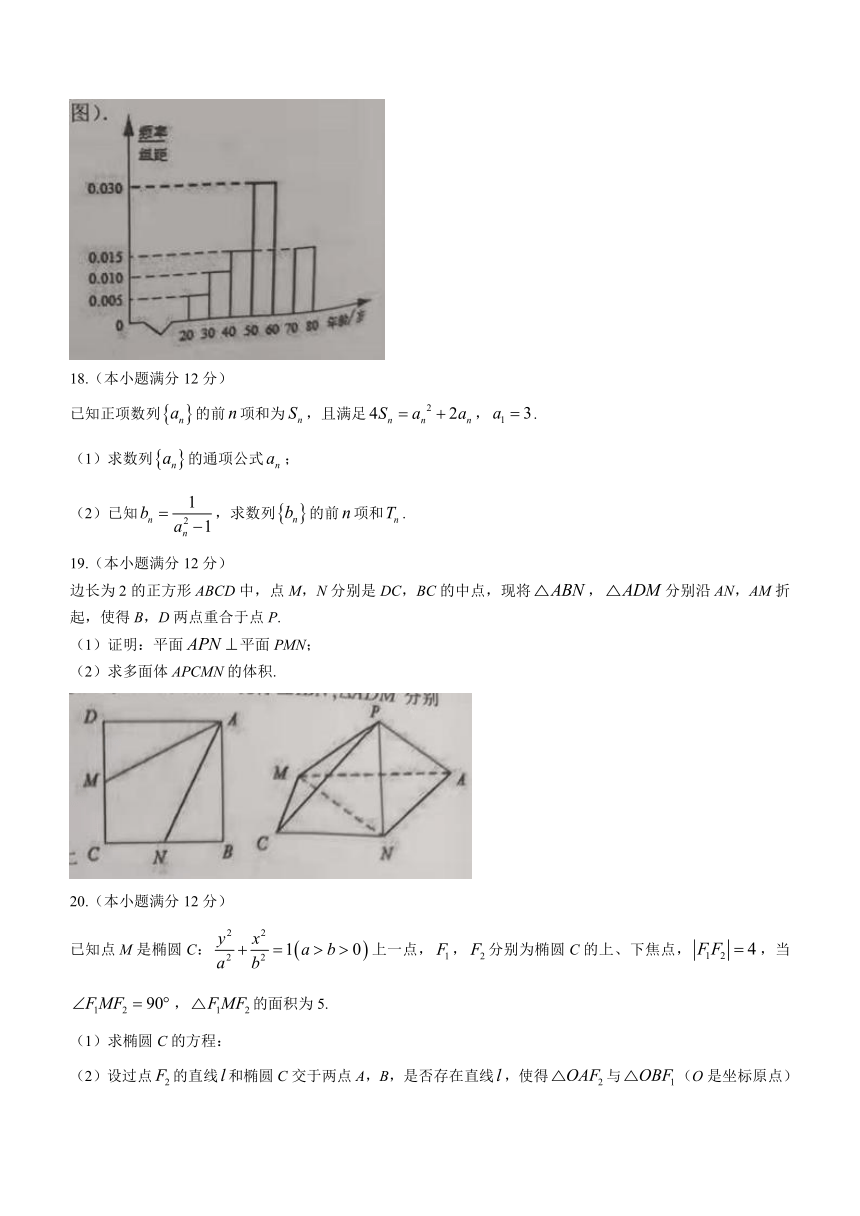
近年来,赣州市坚持把传承弘扬红色基因作为文艺作品创作的主方向,深入挖掘赣南红色文化资源,每年策划一批红色题材的创作选题,推出一批精品力作.2021年,在中国共产党建党一百周年之际,从众多作品中选取了100件进行会展,被选取作品的创作者的年龄(单位:岁)集中在内,根据统计,得到频率分布直方图(如图).
(1)根据频率分布直方图,求年龄在的人数以及这100位创作者年龄的中位数(精确到0.1);
(2)从这100位创作者中采用分层抽样的方法选出20位参加交流会,再从前三组中选出2人的作品整理入册,求这2人中至多有1人的年龄在的概率.
18.(本小题满分12分)
已知正项数列的前项和为,且满足,.
(1)求数列的通项公式;
(2)已知,求数列的前项和.
19.(本小题满分12分)
边长为2的正方形ABCD中,点M,N分别是DC,BC的中点,现将,分别沿AN,AM折起,使得B,D两点重合于点P.
(1)证明:平面平面PMN;
(2)求多面体APCMN的体积.
20.(本小题满分12分)
已知点M是椭圆C:上一点,,分别为椭圆C的上、下焦点,,当,的面积为5.
(1)求椭圆C的方程:
(2)设过点的直线和椭圆C交于两点A,B,是否存在直线,使得与(O是坐标原点)的面积比值为5:7.若存在,求出直线的方程:若不存在,说明理由。
21.(本小题满分12分)
已知函数.
(1)当时,求函数的极值;
(2)若不等式在上恒成立,求实数的最大整数.
(二)选考题(共10分.请考生在第22,23题中任选--题作答.如果多做,则按所做的第一题计分)
22.(本小题满分10分)[选修4-4:坐标系与参数方程]
曲线C的参数方程为(m为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求曲线C的普通方程和直线的直角坐标方程;
(2)已知点,若直线与曲线C交于P,Q两点,求的值.
23.(本小题满分10分)[选修4-5:不等式选讲]
已知函数.
(1)当时,求的解集:
(2)若的解集包含,求实数的取值范围.
赣州市2021~2022学年度第一学期期末考试
高三数学(文科)参考答案
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10 11 12
C A D A C D C D B C B A
二、填空题(本大题共4小题,每小题5分,共20分)
13.2或3 14. 15.3 16.4
三、解答题(本大题共6小题,共70分,解答写出必要的文字说明、演算过程及步骤)
17.解(1)由图可知,年龄在的频率为
所以年龄在的人数为(人),
所以前三组的频率和为,
前四组的频率和为
所以中位数落在第四组,设为,
因此有即
所以中位数是56.7.
(2)依题意按照分层抽样,年龄在的人数为(人)
年龄在的人数为(人)
年龄在的人数为(人)
所以前三组共有6人,从6人中任意抽取2人的基本事件共15个,
其中至多有1人来自的基本事件有12个,
故至多有1人来自的概率为.
18.解(1)当时,,
∴,
整理得
因为
∴
当时,,解得:或
因为,∴
所以是以为首项,以为公差的等差数列,
即
(2)由(1)得
所以
∴.
19.解(1)证明:在正方形中有,
∴,
所以平面PMN
而平面APN
所以平面面PMN
(2)解:易知,,∴
∴
由得(其中h为点P到底面AMN的距离)
即
∴
因此该多面体的体积.
20.解(1)由
由
而
∴
∴
∴
即椭圆的标准方程为
(2)假设满意条件的直线存在,
当直线的斜率不存在时,不合题意,
不妨设直线:,,
联立得,
所以
因为,得
即(3)
由(1),(2),(3),得
所以直线的方程为.
21.解(1)当时
所以
由得或;由得;
即在和上单调递增,在上单调递减;
所以的极大值为,极小值为.
(2)由于
原不等式可化为
整理得在恒成立
法一(整体构造):设,
则
①当即时,在恒成立
即在上为增函数;
满足题意;
②当即时,由得;由得
即在上为减函数,在上为增函数;
∴满足题意;
即
令
∴在上恒成立,即在上为增函数
又,
所以存在唯一实数使得
因此实数的最大整数为2.
法二(分离参数):由在恒成立
得在恒成立
即在恒成立
设,则
令,则
所以在上为增函数
又,
所以存在唯一实数使得
则在上为减函数,在上为增函数
∴,而即
∴
因此实数的最大整数为2.
22.解:(1)由消去得
∵∴
∴∴
(2)直线:点,则直线的倾斜角为,
则直线的参数为方程(为参数),
令P,Q两点对应的参数为,
把代入得
∴,,
∴,
∴
23.解:(1)当时,
①当时,,∴,
∴
②当时,,∴,
∴
③当时,,∴,∴无解
综上所述:,解集为.
(2)由题意可知当时不等式恒成立
∴当时,恒成立
∴当时,恒成立
∴当时,恒成立
∴当时,恒成立
∴,即.
高三数学(文科)试卷
2022年1月
第I卷 (选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数(为虚数单位)的共轭复数为
A. B. C. D.
2.已知集合,,则
A. B. C. D.
3.某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行001,002,…,599,600.从中抽取60个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第6个样本编号是
A.457 B.328 C.253 D.072
4.已知等比数列的各项均为正数,且,则
A.6 B.9 C.27 D.81
5.已知双曲线的一条渐近线方程为,且与椭圆有公共焦点,则双曲线的标准方程为
A. B. C. D.
6.已知实数满足,则直线与圆有公共点的概率为
A. B. C. D.
7.若,则
A. B. C. D.
8.已知函数的图像恒过的定点,且点在直线上,则的最小值为
A.4 B.3 C.2 D.1
9.铸于明嘉靖十二年的泰山岱庙铁塔,造型质朴雄伟,原有十三级,抗日战争中被日军飞机炸毁,现仅存三级,它的底座近似圆形(如图1).我国古代工匠已经知道,将长方体砖块以某个固定的角度相接就可砌出近似圆形的建筑,现存铁塔的底座是用10块一样的长方体砖块砌成的近似圆形的墙面,每块长方体砖块底面较长的边长为1个单位,相邻两块砖之间的夹角固定为36°,如图2,则此近似圆形墙面内部所能容纳最大圆的半径是
A. B. C. D.
10.在下列五个命题中,其中正确的个数为
①命题“,都有”的否定为“,有”;
②已知,,若与夹角为锐角,则的取值范围是;
③“”成立的一个充分不必要条件是“”;
④已知是一条直线,,是两个不同的平面,若,,则.
⑤函数的图像向左平移个单位后所得函数解析式为.
A.4 B.3 C.2 D.1
11.已知正方体的棱长为6,则过,,三点的平面与该正方体内切球截面的面积为
A.3π B.6π C.9π D.12π
2.已知是定义在上的奇函数,且当时,都有不等式成立,若,,,则a,b,c的大小关系是
A. B. C. D.
第Ⅱ卷 (非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分.)
13.已知向量,,若,则____________.
14.设曲线在点处的切线与曲线在点P处的切线互相平行,则点P的坐标为___________.
15.抛物线:的焦点为F,点A,B,C在E上,O是坐标原点,若点F为的重心,,,的面积分别为,,.则___________.
16.已知a,b,c分别为的三个内角A,B,C的对边,,且,O是内一点,且满足为,,则___________.
三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤。第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答)
(一)必考题(共60分)
17.(本小题满分12分)
近年来,赣州市坚持把传承弘扬红色基因作为文艺作品创作的主方向,深入挖掘赣南红色文化资源,每年策划一批红色题材的创作选题,推出一批精品力作.2021年,在中国共产党建党一百周年之际,从众多作品中选取了100件进行会展,被选取作品的创作者的年龄(单位:岁)集中在内,根据统计,得到频率分布直方图(如图).
(1)根据频率分布直方图,求年龄在的人数以及这100位创作者年龄的中位数(精确到0.1);
(2)从这100位创作者中采用分层抽样的方法选出20位参加交流会,再从前三组中选出2人的作品整理入册,求这2人中至多有1人的年龄在的概率.
18.(本小题满分12分)
已知正项数列的前项和为,且满足,.
(1)求数列的通项公式;
(2)已知,求数列的前项和.
19.(本小题满分12分)
边长为2的正方形ABCD中,点M,N分别是DC,BC的中点,现将,分别沿AN,AM折起,使得B,D两点重合于点P.
(1)证明:平面平面PMN;
(2)求多面体APCMN的体积.
20.(本小题满分12分)
已知点M是椭圆C:上一点,,分别为椭圆C的上、下焦点,,当,的面积为5.
(1)求椭圆C的方程:
(2)设过点的直线和椭圆C交于两点A,B,是否存在直线,使得与(O是坐标原点)的面积比值为5:7.若存在,求出直线的方程:若不存在,说明理由。
21.(本小题满分12分)
已知函数.
(1)当时,求函数的极值;
(2)若不等式在上恒成立,求实数的最大整数.
(二)选考题(共10分.请考生在第22,23题中任选--题作答.如果多做,则按所做的第一题计分)
22.(本小题满分10分)[选修4-4:坐标系与参数方程]
曲线C的参数方程为(m为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线的极坐标方程为.
(1)求曲线C的普通方程和直线的直角坐标方程;
(2)已知点,若直线与曲线C交于P,Q两点,求的值.
23.(本小题满分10分)[选修4-5:不等式选讲]
已知函数.
(1)当时,求的解集:
(2)若的解集包含,求实数的取值范围.
赣州市2021~2022学年度第一学期期末考试
高三数学(文科)参考答案
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10 11 12
C A D A C D C D B C B A
二、填空题(本大题共4小题,每小题5分,共20分)
13.2或3 14. 15.3 16.4
三、解答题(本大题共6小题,共70分,解答写出必要的文字说明、演算过程及步骤)
17.解(1)由图可知,年龄在的频率为
所以年龄在的人数为(人),
所以前三组的频率和为,
前四组的频率和为
所以中位数落在第四组,设为,
因此有即
所以中位数是56.7.
(2)依题意按照分层抽样,年龄在的人数为(人)
年龄在的人数为(人)
年龄在的人数为(人)
所以前三组共有6人,从6人中任意抽取2人的基本事件共15个,
其中至多有1人来自的基本事件有12个,
故至多有1人来自的概率为.
18.解(1)当时,,
∴,
整理得
因为
∴
当时,,解得:或
因为,∴
所以是以为首项,以为公差的等差数列,
即
(2)由(1)得
所以
∴.
19.解(1)证明:在正方形中有,
∴,
所以平面PMN
而平面APN
所以平面面PMN
(2)解:易知,,∴
∴
由得(其中h为点P到底面AMN的距离)
即
∴
因此该多面体的体积.
20.解(1)由
由
而
∴
∴
∴
即椭圆的标准方程为
(2)假设满意条件的直线存在,
当直线的斜率不存在时,不合题意,
不妨设直线:,,
联立得,
所以
因为,得
即(3)
由(1),(2),(3),得
所以直线的方程为.
21.解(1)当时
所以
由得或;由得;
即在和上单调递增,在上单调递减;
所以的极大值为,极小值为.
(2)由于
原不等式可化为
整理得在恒成立
法一(整体构造):设,
则
①当即时,在恒成立
即在上为增函数;
满足题意;
②当即时,由得;由得
即在上为减函数,在上为增函数;
∴满足题意;
即
令
∴在上恒成立,即在上为增函数
又,
所以存在唯一实数使得
因此实数的最大整数为2.
法二(分离参数):由在恒成立
得在恒成立
即在恒成立
设,则
令,则
所以在上为增函数
又,
所以存在唯一实数使得
则在上为减函数,在上为增函数
∴,而即
∴
因此实数的最大整数为2.
22.解:(1)由消去得
∵∴
∴∴
(2)直线:点,则直线的倾斜角为,
则直线的参数为方程(为参数),
令P,Q两点对应的参数为,
把代入得
∴,,
∴,
∴
23.解:(1)当时,
①当时,,∴,
∴
②当时,,∴,
∴
③当时,,∴,∴无解
综上所述:,解集为.
(2)由题意可知当时不等式恒成立
∴当时,恒成立
∴当时,恒成立
∴当时,恒成立
∴当时,恒成立
∴,即.
同课章节目录
