2021-2022学年安徽省合肥市庐江县九年级(上)期末数学试卷(PDF版,含答案)
文档属性
| 名称 | 2021-2022学年安徽省合肥市庐江县九年级(上)期末数学试卷(PDF版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 523.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 16:59:39 | ||
图片预览


文档简介
2021-2022 学年安徽省合肥市庐江县九年级(上)期末数学试卷
一、选择题(本题共 10 小题,每小题 4 分,满分 40 分。请将每小题唯一正确选项前的代
号填入下面的答题栏内)
1.关于 x的方程(a﹣1)x2﹣3x+2=0是一元二次方程,则( )
A.a≠1 B.a=1 C.a>1 D.a≥1
2.下列事件中,属于必然事件的是( )
A.购买一张彩票,中奖
B.从煮熟的鸡蛋里孵出小鸡,神奇
C.篮球队员在罚球线投篮一次,投中
D.实心铅球投入水中,下沉
3.关于 x的一元二次方程 x2+5x﹣m=0的一根是 2,则另一根是( )
A.﹣7 B.7 C.3 D.﹣3
4.随着人们健康生活理念的提高,环保意识也不断增强,以下是回收绿色包装、节水、低
碳四个标志,其中是中心对称图形的是( )
A. B.
C. D.
5.在平面直角坐标系中,将抛物线 y=x2﹣2x+1 先向左平移 3 个单位长度,再向下平移 2
个单位长度,经过两次平移后所得抛物线的顶点坐标是( )
A.(4,2) B.(﹣2,2) C.(4,﹣2) D.(﹣2,﹣2)
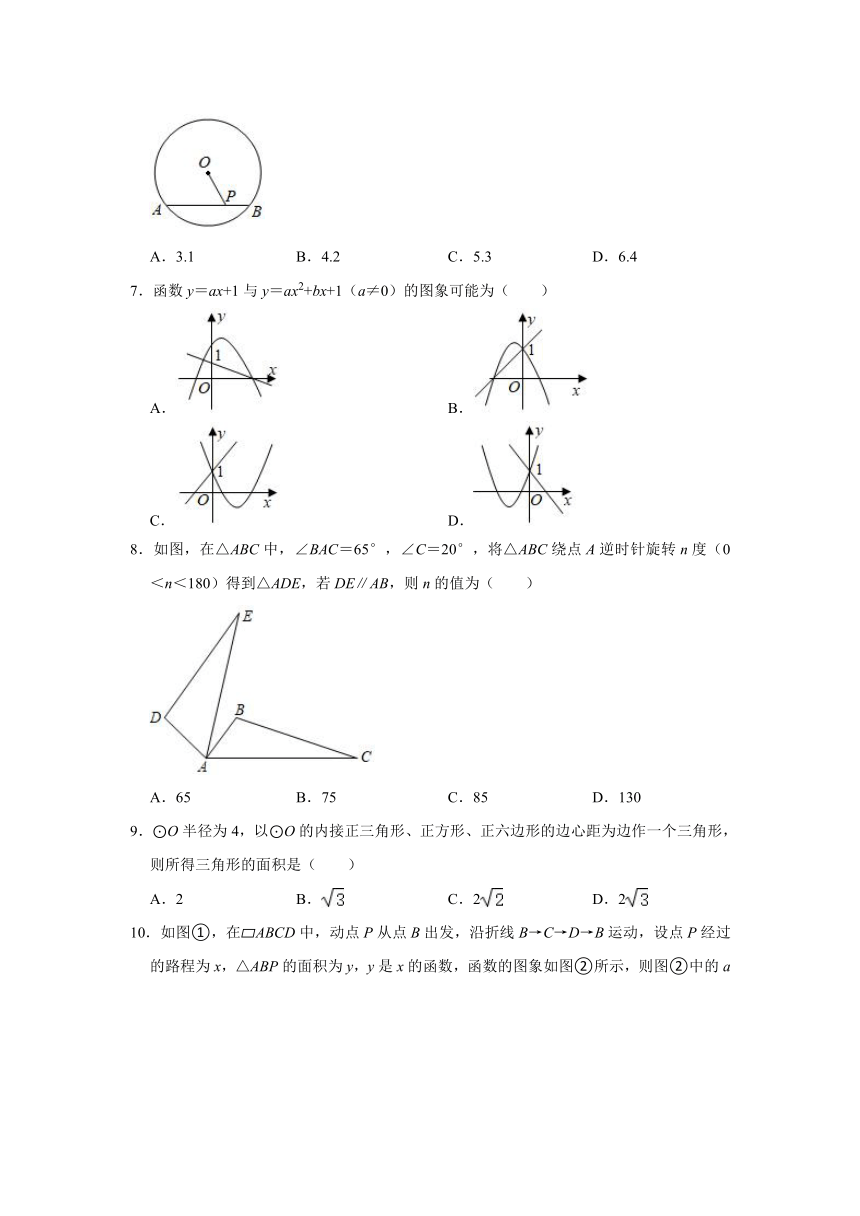
6.如图,⊙O的半径为 5,弦 AB=6,P是弦 AB上的一个动点(不与 A、B重合),下列符
合条件的 OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
7.函数 y=ax+1与 y=ax2+bx+1(a≠0)的图象可能为( )
A. B.
C. D.
8.如图,在△ABC中,∠BAC=65°,∠C=20°,将△ABC绕点 A逆时针旋转 n度(0
<n<180)得到△ADE,若 DE∥AB,则 n的值为( )
A.65 B.75 C.85 D.130
9.⊙O半径为 4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,
则所得三角形的面积是( )
A.2 B. C.2 D.2
10.如图①,在 ABCD中,动点 P从点 B出发,沿折线 B→C→D→B运动,设点 P经过
的路程为 x,△ABP的面积为 y,y是 x的函数,函数的图象如图②所示,则图②中的 a
值为( )
A.3 B.4 C.14 D.18
二、填空题(本题共 4 小题,每小题 5 分,满分 20 分)
11.若点 A(2x﹣1,﹣5)和点 B(3,y﹣3)关于原点对称,则 xy的值为 .
12.标有 A,B,C的三只灯笼按图所示悬挂,每次摘取一只(摘 B前需先摘 C),直到摘完,
则最后一只摘到 B的概率是 .
13.如图,四边形 ABCD内接于⊙O,AD∥BC,BD平分∠ABC,∠A=126°,则∠BDC
的度数为 .
14.如图,在 Rt△ABC中,∠C=90°,AC=6,∠B=30°,点 F在边 AC上,并且 CF=
2,点 E为边 BC上的动点,将△CEF沿直线 EF翻折,点 C落在点 P处,则点 P到边
AB距离的最小值是 .
三、(本题共 2 小题,每小题 8 分,满分 16 分)
15.解方程:x2+2x﹣3=0.
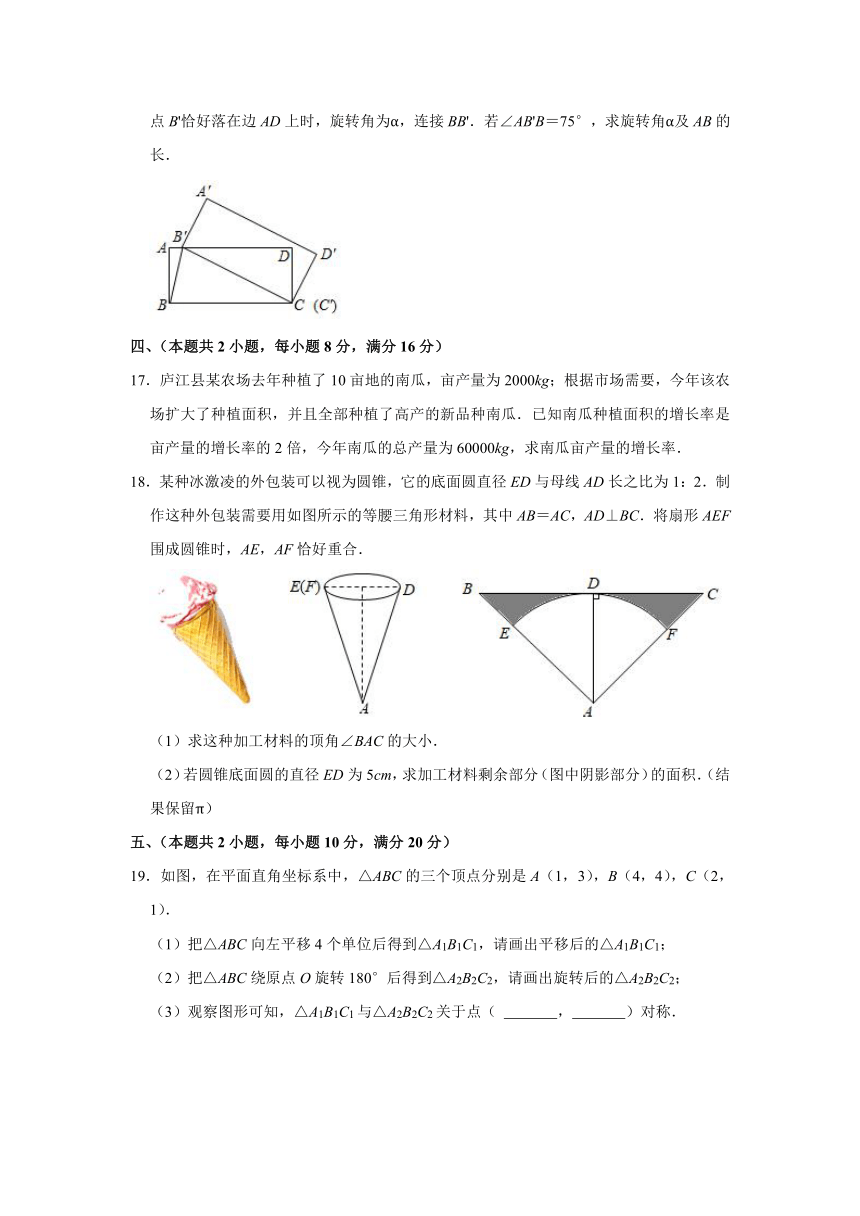
16.如图,矩形 ABCD中,BC=4,将矩形 ABCD绕点 C顺时针旋转得到矩形 A'B'C'D'.当
点 B'恰好落在边 AD上时,旋转角为α,连接 BB'.若∠AB'B=75°,求旋转角α及 AB的
长.
四、(本题共 2 小题,每小题 8 分,满分 16 分)
17.庐江县某农场去年种植了 10亩地的南瓜,亩产量为 2000kg;根据市场需要,今年该农
场扩大了种植面积,并且全部种植了高产的新品种南瓜.已知南瓜种植面积的增长率是
亩产量的增长率的 2倍,今年南瓜的总产量为 60000kg,求南瓜亩产量的增长率.
18.某种冰激凌的外包装可以视为圆锥,它的底面圆直径 ED与母线 AD长之比为 1:2.制
作这种外包装需要用如图所示的等腰三角形材料,其中 AB=AC,AD⊥BC.将扇形 AEF
围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径 ED为 5cm,求加工材料剩余部分(图中阴影部分)的面积.(结
果保留π)
五、(本题共 2 小题,每小题 10 分,满分 20 分)
19.如图,在平面直角坐标系中,△ABC的三个顶点分别是 A(1,3),B(4,4),C(2,
1).
(1)把△ABC向左平移 4个单位后得到△A1B1C1,请画出平移后的△A1B1C1;
(2)把△ABC绕原点 O旋转 180°后得到△A2B2C2,请画出旋转后的△A2B2C2;
(3)观察图形可知,△A1B1C1与△A2B2C2关于点( , )对称.
20.已知一抛物线的顶点为(2,4),图象过点(1,3).
(1)求抛物线的解析式;
(2)动点 P(x,5)能否在抛物线上?请说明理由;
(3)若点 A(a,y1),B(b,y2)都在抛物线上,且 a<b<0,比较 y1,y2的大小,并
说明理由.
六、(本题满分 12 分)
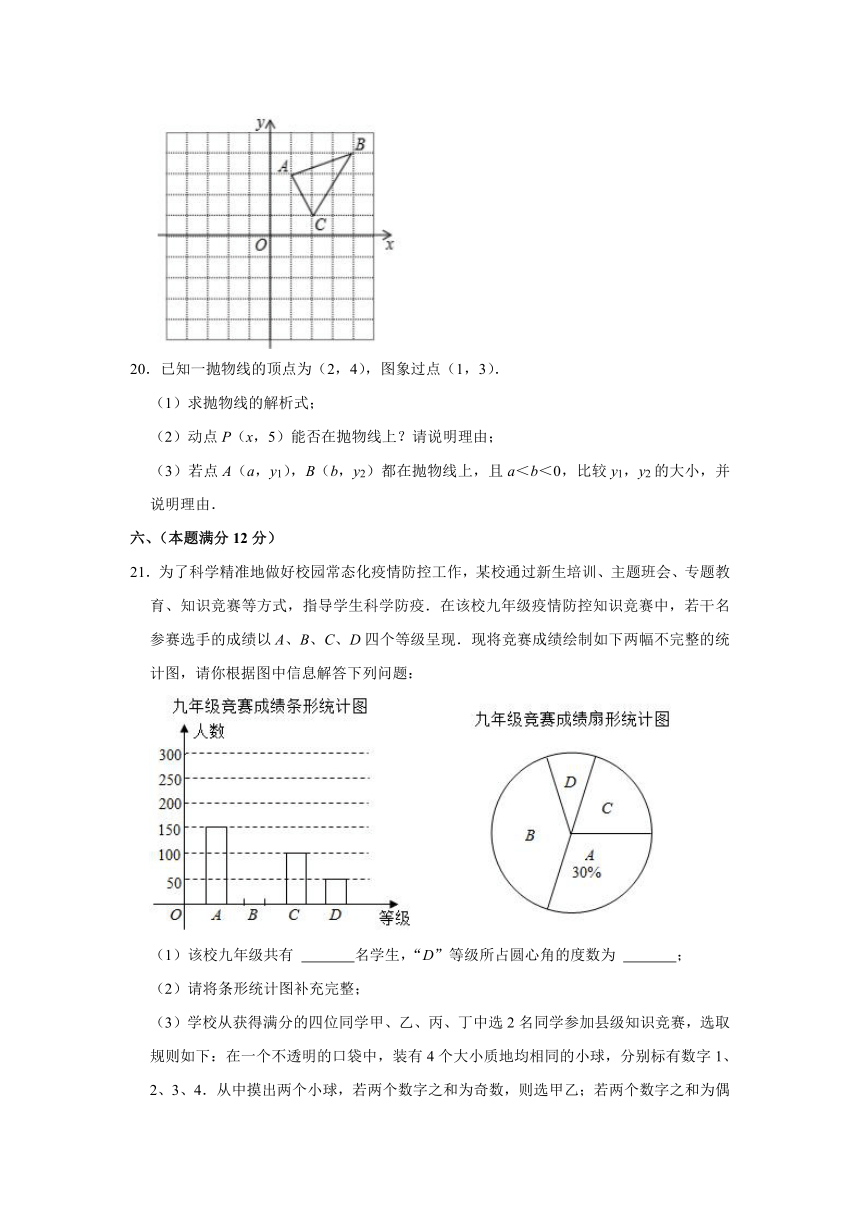
21.为了科学精准地做好校园常态化疫情防控工作,某校通过新生培训、主题班会、专题教
育、知识竞赛等方式,指导学生科学防疫.在该校九年级疫情防控知识竞赛中,若干名
参赛选手的成绩以 A、B、C、D四个等级呈现.现将竞赛成绩绘制如下两幅不完整的统
计图,请你根据图中信息解答下列问题:
(1)该校九年级共有 名学生,“D”等级所占圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)学校从获得满分的四位同学甲、乙、丙、丁中选 2名同学参加县级知识竞赛,选取
规则如下:在一个不透明的口袋中,装有 4个大小质地均相同的小球,分别标有数字 1、
2、3、4.从中摸出两个小球,若两个数字之和为奇数,则选甲乙;若两个数字之和为偶
数,则选丙丁,请用树状图或列表法说明此规则是否合理.
七、(本题满分 12 分)
22.如图,在△ABC中,∠ACB=90°,AC=BC,O点在△ABC内部,⊙O经过 B、C两
点且交 AB于点 D,连接⊙O并延长交线段 AB于点 G,以 GD、GC为邻边作平行四边形
GDEC.
(1)求证:直线 DE是⊙O的切线;
(2)若 DE=7,CE=5,求⊙O的半径.
八、(本题满分 14 分)
23.某超市经销 A、B两种商品.商品 A每千克成本为 20元,经试销发现,该种商品每天
销售量 y(千克)与销售单价 x(元/千克)满足一次函数关系,其每天销售单价、销售量
的对应值如表所示:
销售单价 x(元/ 25 30 35 40
千克)
销售量 y(千克) 50 40 30 20
商品 B的成本为 6元/千克,销售单价为 10元/千克,但每天供货总量只有 60千克,且能
当天销售完.为了让利消费者,超市开展了“买一送一”活动,即买 1千克的商品 A,
免费送 1千克的商品 B.
(1)求 y(千克)与 x(元/千克)之间的函数表达式;
(2)设这两种商品的每天销售总利润为 w元,求出 w(元)与 x的函数关系式;
(3)若商品 A的售价不低于成本,不高于成本的 180%,当销售单价定为多少时,才能
使当天的销售总利润最大?最大利润是多少?(总利润=两种商品的销售总额﹣两种商
品的成本)
庐江县 2021/2022 学年度第一学期期末考试
九年级数学参考答案及评分标准
一、选择题(本题共 10小题,每小题 4分,满分 40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B D B C C C A
二、填空题(本题共 4小题,每小题 5分,满分 20分)
�
11.1; 12. ; 13.99°; 14.
� � � � �.
三、(本题共2小题,每小题 8分,满分 16分)
15.解方程:x� + �x � � = 0.
解:配方法、公式法、因式分解法皆可,方程的根为�� = �,�� =� �.
………………8分
16.解:∵四边形 ABCD是矩形,
∴AD∥BC,
∴∠CBB'=∠AB'B=75°,
由旋转的性质得:CB=CB',
∴∠CB'B=∠CBB'=75°,
∴∠BCB'=180°﹣75°﹣75°=30°,
即旋转角α为 30°.
………………4分
作 B'E⊥BC于 E,如图所示:
则 AB=B'E= CB'=2.
………………8分
四、(本题共 2小题,每小题 8分,满分 16分)
17.解:设南瓜亩产量的增长率为 x,则种植面积的增长率为 2x.
根据题意,得 10(1+2x) 2000(1+x)=60000.
………………4分
解得:x1=0.5,x2=﹣2(不合题意,舍去).
答:南瓜亩产量的增长率为 50%.
………………8分
18.解:(1)设∠BAC=n°.
由题意得π DE= ,AD=2DE,
∴n=90,
∴∠BAC=90°.
………………4分
(2)∵AD=2DE=10(cm),
∴S 阴= BC AD﹣S 扇形 AEF= ×10×20﹣ =(100﹣25π)cm2.
………………8分
五、(本题共 2小题,每小题 10分,满分 20分)
19.解:(1)如图所示,△A1B1C1即为所求;
………………4分
(2)如图所示,△A2B2C2即为所求;
………………8分
(3)由图可得,△A1B1C1与△A2B2C2关于点(﹣2,0)中心对称.
故答案为:﹣2,0.
………………10分
20. 解:(1)设抛物线解析式为 y = a(x � �)� + �,将(1,3)代入得:
� = �(� � �)� + �,解得 a=-1,
∴抛物线的解析式为 y = � (x � �)� + �.
………………3分
(2)动点 P(x,5)不在抛物线上,理由如下:
∵抛物线 y = � (x � �)� + �的最大值为 4,
∴动点 P(x,5)不在抛物线上.
………………6分
(3)∵抛物线的解析式为 y = � (x � �)� + �,
∴抛物线的开口方向向下,对称轴为直线 x = �,
∴当 x<2时,y 随 x 的增大而增大,
又∵点 A(a,y1),B(b,y2)都在抛物线上,且 a<b<0<2,
∴y1<y2 .
………………10 分
六、(本题满分 12 分)
21.解:(1)该校九年级共有学生:150÷30%=500(名),
则 D等级所占圆心角的度数为:360°× =36°,
故答案为:500,36°;
(2)B等级的人数为:500﹣150﹣100﹣50=200(名),
将条形统计图补充完整如下:
(3)此规则不合理,理由如下:
画树状图如图:
共有 12种等可能的结果,选甲乙的结果有 8种,选丙丁的结果有 4种,
∴选甲乙的概率为 = ,选丙丁的概率为 = ,
∵ > ,
∴此规则不合理.
七、(本题满分 12分)
22.(1)证明: 连接 OD,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°;
∵四边形 GDEC 是平行四边形,
∴DE∥CG,
∴∠ODE+∠COD=180°,
∴∠ODE=90°,
即:OD⊥DE;
∵OD 是半径,
∴直线 DE 是⊙O 的切线.
………………6分
(2)解:设⊙O 的半径为 r.
∵四边形 GDEC 是平行四边形,
∴CE=GD=5,GC=DE=7,
∵∠DOG=90°,
∴�t� + �t� = tt�,即
�� + (�� �)� = ��,解得�� = �,��� = �,
当�� = �时,OG=4,此时点 G 在⊙O外,不符合题意,舍去.
∴r=4,即⊙O半径为 4.
………………12 分
八、(本题满分 14分)
23.解:(1)设 y与 x之间的函数表达式为 y=kx+b(k≠0),将表中数据(30,40)、
(40,20)代入得:
,
解得: ,
∴y与 x之间的函数表达式为 y=﹣2x+100;
………………4分
(2)由 y≤60,得 x≥20,
由 y≥0,得 x≤50,
∴20≤x≤50.
………………6分
w=(x﹣20)(﹣2x+100)﹣6×(﹣2x+100)+(10﹣6)[60﹣(﹣2x+100)]
=﹣2x2+160x﹣2760(20≤x≤50);
………………10 分
(3)20×180%=36,
由题意知 20≤x≤36,
w=﹣2x2+160x﹣2760=﹣2(x﹣40)2+440,
∵﹣2<0,
∴x<40时,w随 x的增大而增大,
∴x=36时,w的最大值=﹣2×(36﹣40)2+440=408,
答:当销售单价定为 36元时,才能使当天的销售总利润最大,最大利润是 408元.
………………14 分
一、选择题(本题共 10 小题,每小题 4 分,满分 40 分。请将每小题唯一正确选项前的代
号填入下面的答题栏内)
1.关于 x的方程(a﹣1)x2﹣3x+2=0是一元二次方程,则( )
A.a≠1 B.a=1 C.a>1 D.a≥1
2.下列事件中,属于必然事件的是( )
A.购买一张彩票,中奖
B.从煮熟的鸡蛋里孵出小鸡,神奇
C.篮球队员在罚球线投篮一次,投中
D.实心铅球投入水中,下沉
3.关于 x的一元二次方程 x2+5x﹣m=0的一根是 2,则另一根是( )
A.﹣7 B.7 C.3 D.﹣3
4.随着人们健康生活理念的提高,环保意识也不断增强,以下是回收绿色包装、节水、低
碳四个标志,其中是中心对称图形的是( )
A. B.
C. D.
5.在平面直角坐标系中,将抛物线 y=x2﹣2x+1 先向左平移 3 个单位长度,再向下平移 2
个单位长度,经过两次平移后所得抛物线的顶点坐标是( )
A.(4,2) B.(﹣2,2) C.(4,﹣2) D.(﹣2,﹣2)
6.如图,⊙O的半径为 5,弦 AB=6,P是弦 AB上的一个动点(不与 A、B重合),下列符
合条件的 OP的值可以是( )
A.3.1 B.4.2 C.5.3 D.6.4
7.函数 y=ax+1与 y=ax2+bx+1(a≠0)的图象可能为( )
A. B.
C. D.
8.如图,在△ABC中,∠BAC=65°,∠C=20°,将△ABC绕点 A逆时针旋转 n度(0
<n<180)得到△ADE,若 DE∥AB,则 n的值为( )
A.65 B.75 C.85 D.130
9.⊙O半径为 4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,
则所得三角形的面积是( )
A.2 B. C.2 D.2
10.如图①,在 ABCD中,动点 P从点 B出发,沿折线 B→C→D→B运动,设点 P经过
的路程为 x,△ABP的面积为 y,y是 x的函数,函数的图象如图②所示,则图②中的 a
值为( )
A.3 B.4 C.14 D.18
二、填空题(本题共 4 小题,每小题 5 分,满分 20 分)
11.若点 A(2x﹣1,﹣5)和点 B(3,y﹣3)关于原点对称,则 xy的值为 .
12.标有 A,B,C的三只灯笼按图所示悬挂,每次摘取一只(摘 B前需先摘 C),直到摘完,
则最后一只摘到 B的概率是 .
13.如图,四边形 ABCD内接于⊙O,AD∥BC,BD平分∠ABC,∠A=126°,则∠BDC
的度数为 .
14.如图,在 Rt△ABC中,∠C=90°,AC=6,∠B=30°,点 F在边 AC上,并且 CF=
2,点 E为边 BC上的动点,将△CEF沿直线 EF翻折,点 C落在点 P处,则点 P到边
AB距离的最小值是 .
三、(本题共 2 小题,每小题 8 分,满分 16 分)
15.解方程:x2+2x﹣3=0.
16.如图,矩形 ABCD中,BC=4,将矩形 ABCD绕点 C顺时针旋转得到矩形 A'B'C'D'.当
点 B'恰好落在边 AD上时,旋转角为α,连接 BB'.若∠AB'B=75°,求旋转角α及 AB的
长.
四、(本题共 2 小题,每小题 8 分,满分 16 分)
17.庐江县某农场去年种植了 10亩地的南瓜,亩产量为 2000kg;根据市场需要,今年该农
场扩大了种植面积,并且全部种植了高产的新品种南瓜.已知南瓜种植面积的增长率是
亩产量的增长率的 2倍,今年南瓜的总产量为 60000kg,求南瓜亩产量的增长率.
18.某种冰激凌的外包装可以视为圆锥,它的底面圆直径 ED与母线 AD长之比为 1:2.制
作这种外包装需要用如图所示的等腰三角形材料,其中 AB=AC,AD⊥BC.将扇形 AEF
围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径 ED为 5cm,求加工材料剩余部分(图中阴影部分)的面积.(结
果保留π)
五、(本题共 2 小题,每小题 10 分,满分 20 分)
19.如图,在平面直角坐标系中,△ABC的三个顶点分别是 A(1,3),B(4,4),C(2,
1).
(1)把△ABC向左平移 4个单位后得到△A1B1C1,请画出平移后的△A1B1C1;
(2)把△ABC绕原点 O旋转 180°后得到△A2B2C2,请画出旋转后的△A2B2C2;
(3)观察图形可知,△A1B1C1与△A2B2C2关于点( , )对称.
20.已知一抛物线的顶点为(2,4),图象过点(1,3).
(1)求抛物线的解析式;
(2)动点 P(x,5)能否在抛物线上?请说明理由;
(3)若点 A(a,y1),B(b,y2)都在抛物线上,且 a<b<0,比较 y1,y2的大小,并
说明理由.
六、(本题满分 12 分)
21.为了科学精准地做好校园常态化疫情防控工作,某校通过新生培训、主题班会、专题教
育、知识竞赛等方式,指导学生科学防疫.在该校九年级疫情防控知识竞赛中,若干名
参赛选手的成绩以 A、B、C、D四个等级呈现.现将竞赛成绩绘制如下两幅不完整的统
计图,请你根据图中信息解答下列问题:
(1)该校九年级共有 名学生,“D”等级所占圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)学校从获得满分的四位同学甲、乙、丙、丁中选 2名同学参加县级知识竞赛,选取
规则如下:在一个不透明的口袋中,装有 4个大小质地均相同的小球,分别标有数字 1、
2、3、4.从中摸出两个小球,若两个数字之和为奇数,则选甲乙;若两个数字之和为偶
数,则选丙丁,请用树状图或列表法说明此规则是否合理.
七、(本题满分 12 分)
22.如图,在△ABC中,∠ACB=90°,AC=BC,O点在△ABC内部,⊙O经过 B、C两
点且交 AB于点 D,连接⊙O并延长交线段 AB于点 G,以 GD、GC为邻边作平行四边形
GDEC.
(1)求证:直线 DE是⊙O的切线;
(2)若 DE=7,CE=5,求⊙O的半径.
八、(本题满分 14 分)
23.某超市经销 A、B两种商品.商品 A每千克成本为 20元,经试销发现,该种商品每天
销售量 y(千克)与销售单价 x(元/千克)满足一次函数关系,其每天销售单价、销售量
的对应值如表所示:
销售单价 x(元/ 25 30 35 40
千克)
销售量 y(千克) 50 40 30 20
商品 B的成本为 6元/千克,销售单价为 10元/千克,但每天供货总量只有 60千克,且能
当天销售完.为了让利消费者,超市开展了“买一送一”活动,即买 1千克的商品 A,
免费送 1千克的商品 B.
(1)求 y(千克)与 x(元/千克)之间的函数表达式;
(2)设这两种商品的每天销售总利润为 w元,求出 w(元)与 x的函数关系式;
(3)若商品 A的售价不低于成本,不高于成本的 180%,当销售单价定为多少时,才能
使当天的销售总利润最大?最大利润是多少?(总利润=两种商品的销售总额﹣两种商
品的成本)
庐江县 2021/2022 学年度第一学期期末考试
九年级数学参考答案及评分标准
一、选择题(本题共 10小题,每小题 4分,满分 40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B D B C C C A
二、填空题(本题共 4小题,每小题 5分,满分 20分)
�
11.1; 12. ; 13.99°; 14.
� � � � �.
三、(本题共2小题,每小题 8分,满分 16分)
15.解方程:x� + �x � � = 0.
解:配方法、公式法、因式分解法皆可,方程的根为�� = �,�� =� �.
………………8分
16.解:∵四边形 ABCD是矩形,
∴AD∥BC,
∴∠CBB'=∠AB'B=75°,
由旋转的性质得:CB=CB',
∴∠CB'B=∠CBB'=75°,
∴∠BCB'=180°﹣75°﹣75°=30°,
即旋转角α为 30°.
………………4分
作 B'E⊥BC于 E,如图所示:
则 AB=B'E= CB'=2.
………………8分
四、(本题共 2小题,每小题 8分,满分 16分)
17.解:设南瓜亩产量的增长率为 x,则种植面积的增长率为 2x.
根据题意,得 10(1+2x) 2000(1+x)=60000.
………………4分
解得:x1=0.5,x2=﹣2(不合题意,舍去).
答:南瓜亩产量的增长率为 50%.
………………8分
18.解:(1)设∠BAC=n°.
由题意得π DE= ,AD=2DE,
∴n=90,
∴∠BAC=90°.
………………4分
(2)∵AD=2DE=10(cm),
∴S 阴= BC AD﹣S 扇形 AEF= ×10×20﹣ =(100﹣25π)cm2.
………………8分
五、(本题共 2小题,每小题 10分,满分 20分)
19.解:(1)如图所示,△A1B1C1即为所求;
………………4分
(2)如图所示,△A2B2C2即为所求;
………………8分
(3)由图可得,△A1B1C1与△A2B2C2关于点(﹣2,0)中心对称.
故答案为:﹣2,0.
………………10分
20. 解:(1)设抛物线解析式为 y = a(x � �)� + �,将(1,3)代入得:
� = �(� � �)� + �,解得 a=-1,
∴抛物线的解析式为 y = � (x � �)� + �.
………………3分
(2)动点 P(x,5)不在抛物线上,理由如下:
∵抛物线 y = � (x � �)� + �的最大值为 4,
∴动点 P(x,5)不在抛物线上.
………………6分
(3)∵抛物线的解析式为 y = � (x � �)� + �,
∴抛物线的开口方向向下,对称轴为直线 x = �,
∴当 x<2时,y 随 x 的增大而增大,
又∵点 A(a,y1),B(b,y2)都在抛物线上,且 a<b<0<2,
∴y1<y2 .
………………10 分
六、(本题满分 12 分)
21.解:(1)该校九年级共有学生:150÷30%=500(名),
则 D等级所占圆心角的度数为:360°× =36°,
故答案为:500,36°;
(2)B等级的人数为:500﹣150﹣100﹣50=200(名),
将条形统计图补充完整如下:
(3)此规则不合理,理由如下:
画树状图如图:
共有 12种等可能的结果,选甲乙的结果有 8种,选丙丁的结果有 4种,
∴选甲乙的概率为 = ,选丙丁的概率为 = ,
∵ > ,
∴此规则不合理.
七、(本题满分 12分)
22.(1)证明: 连接 OD,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°;
∵四边形 GDEC 是平行四边形,
∴DE∥CG,
∴∠ODE+∠COD=180°,
∴∠ODE=90°,
即:OD⊥DE;
∵OD 是半径,
∴直线 DE 是⊙O 的切线.
………………6分
(2)解:设⊙O 的半径为 r.
∵四边形 GDEC 是平行四边形,
∴CE=GD=5,GC=DE=7,
∵∠DOG=90°,
∴�t� + �t� = tt�,即
�� + (�� �)� = ��,解得�� = �,��� = �,
当�� = �时,OG=4,此时点 G 在⊙O外,不符合题意,舍去.
∴r=4,即⊙O半径为 4.
………………12 分
八、(本题满分 14分)
23.解:(1)设 y与 x之间的函数表达式为 y=kx+b(k≠0),将表中数据(30,40)、
(40,20)代入得:
,
解得: ,
∴y与 x之间的函数表达式为 y=﹣2x+100;
………………4分
(2)由 y≤60,得 x≥20,
由 y≥0,得 x≤50,
∴20≤x≤50.
………………6分
w=(x﹣20)(﹣2x+100)﹣6×(﹣2x+100)+(10﹣6)[60﹣(﹣2x+100)]
=﹣2x2+160x﹣2760(20≤x≤50);
………………10 分
(3)20×180%=36,
由题意知 20≤x≤36,
w=﹣2x2+160x﹣2760=﹣2(x﹣40)2+440,
∵﹣2<0,
∴x<40时,w随 x的增大而增大,
∴x=36时,w的最大值=﹣2×(36﹣40)2+440=408,
答:当销售单价定为 36元时,才能使当天的销售总利润最大,最大利润是 408元.
………………14 分
同课章节目录
