安徽六安市霍邱县2021-2022学年九年级上学期期末统考数学试卷(PDF版,含答案)
文档属性
| 名称 | 安徽六安市霍邱县2021-2022学年九年级上学期期末统考数学试卷(PDF版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 19:00:28 | ||
图片预览



文档简介
安徽六安市霍邱县 2021-2022 学年九上期末(统考)数学试卷(含答案)
温馨提示:本试卷内容沪科版九上全册第 21 章~23 章、共 4 页八大题、23小题,满分 150 分,时间 120 分钟
一、选择题(本大题共 10 小题,每小题 4 分,满分 40 分)
1、已知 2x=3y(xy≠0),那么下列比例式中成立的是( )
x 2 x 3
A
x y x y
y 3 B
C D
2 3 3 2 2 y
2、将抛物线 y=x 向上平移 3 个单位长度,再向右平移 5 个单位长度,所得的抛物线为( )
A.y=(x+3) +5 B.y=(x-3) +5 C.y=(x-5) +3 D.y=(x+5) +3
3、若角 a的余角是 30°,则 cosa 的值是( )
3 3 2 1
A B C D
3 2 3 2
a2 1
4、已知点 A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数 y= (a 是常数)的图象上,且 y1 <y2<0<y3,x
则 x1、x2、x3 的大小关系为( )
A.x2>x1>x3 B.x1>x2>x3 C.x3>x2>x1 D.x3>x1>x2
k
5、在同一平面直角坐标系中,一次函数 y1=k1x+b 与反比例函数 y2=
2 (x>0)的图象如图所示,则当 y >y 时,自
x 1 2
变量 x的取值范围为( )
A.0<x<l B.x>3 C.1<x<3 D.x<1
第 5题图 第 6题图 第 7题图 第 8题图 第 9题图
6、生活中到处可见黄金分割的美,如上图,在设计人体雕像时,使雕像的腰部以下 a与全身 b的高度比值接近 0. 618,
可以增加视觉美感,若图中 b为 2米,则 a约为( )
A.1.52 米 B.1.38 米 C.1.42 米 D.1.24 米.
7、如图,某停车场入口的栏杆 AB ,从水平位置绕点 0 旋转到 A'B'的位置,已知 AO 的长为 4米,若栏杆的旋转角
∠A0A' =α,则栏杆 A端升高的高度为( )
4 4
A 米 B 4sinα米 C 米 D cosα米
sin cos
k
8、如图,ΔABO 的顶点 A 在函数 y= (x>0)的图象上,∠ABO=90°,过 AO 边的三等分点 M、N分别作 x轴的平行
x
线交 AB于点 P、Q,若四边形 MNQP 的面积为 3,则 k的值为( )
A.9 B.12 C.18 D.15
9、如图,在ΔABC 中,点 D 在 BC 上,连接 AD,点 E在 AC 上,过点 E作 EF//BC,交 AD 于点 F,过点 E作 EC//AB,
交 BC于点 G,则下列式子一定正确的是( )
A AE:EC=EF:CD B AF:FD=BG:GC C EG:AB=EF:CD D CG:BC=AF:AD
1
10、如图,正ΔABC 的边长为 4,点 P为 BC 边上的任意一点(不与点 B、C重合),且∠APD=60°,PD 交 AB 于点 D,
设 BP=x,BD=y,则 y 关于 x 的函数图象大致是( )
A B C D
二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)
k
11、已知反比例函数 y= 的图象经过点( -3,4),则 k的值是
x
12、抛物线 y=3(x-1) +8 的顶点坐标为
13、如图,矩形 ABCD 中,AB=2,E 为 CD 的中点,连接 AE、BD 交于点 P,过点 P作 PQ⊥BC于点 Q,则 PQ=
第 13 题图 第 14题图
14、如图,在 RtΔABC 中,∠ACB=90°,0为 AB 的中点,0D平分∠AOC 交 AC 于点 G,0D =0A,BD 分别与 AC,0C 交
于点 E、F,连接 AD、CD,则 OG:BC 的值为 ;若 CE=CF,则 CF:OF 的值为
三、(本大题共 2小题,每小题 8分,总计 16 分)
15、计算: 3 8 2 2cos600 (3.14 ) 0
16、如图,在边长为 1个单位长度的小正方形组戒的网格中,△ABC 与△A'B'C'以点 0 为位似中心,且它们的顶点都
为网格线的交点
(1)在图中画出点 0(要保留画图痕迹),并直接写出:△ABC 与△A'B'C'的位似比是
(2)请在此网格中,以点 C为位似中心,再画一个△A1B1C2,使它与△ABC 的位似比等于 2:1
四、(本大题共 2小题,每小题 8分,总计 16 分)
17、如图,在ΔABC 中,D、E、F分别是 AB、BC 上的点,且 DE//AC、AE//DF,BD:AD=3:2,求 EF 和 FC 的长.
2
18、(1)用尺规作图作 AB 的垂直平分线 EF,交 AB 于点 E,交 AC 于点 F(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求 EF的长度;
五、(本大题共 2小题,每小题 10 分,总计 20 分)
19、为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案他们在河南岸的点 A处测得河北岸的
树 H恰好在 A的正北方向测量方案与数据如下表:
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到 0.1m,参考数据:sin70°≈0.94,sin35°≈0. 57,tan70°
≈2.75,tan35°≈0.70)
k
20、如图,点 A(-2,y1)、B(-6,y2)在反比例函数 y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为 C、D,x
AC 与 BD 相交于点 E
(1)根据图象直接写出 y1、y2 的大小关系,并通过计算加以验证;
(2)结合以上信息,从①四边形 OCED 的面积为 2;②BE=2AE 这两个条件中任选一个作为补充条件,求 k的值;
你选择的条件是_ (只填序号)
3
六、(本大题共 1小题,每小题 12 分,总计 12 分)
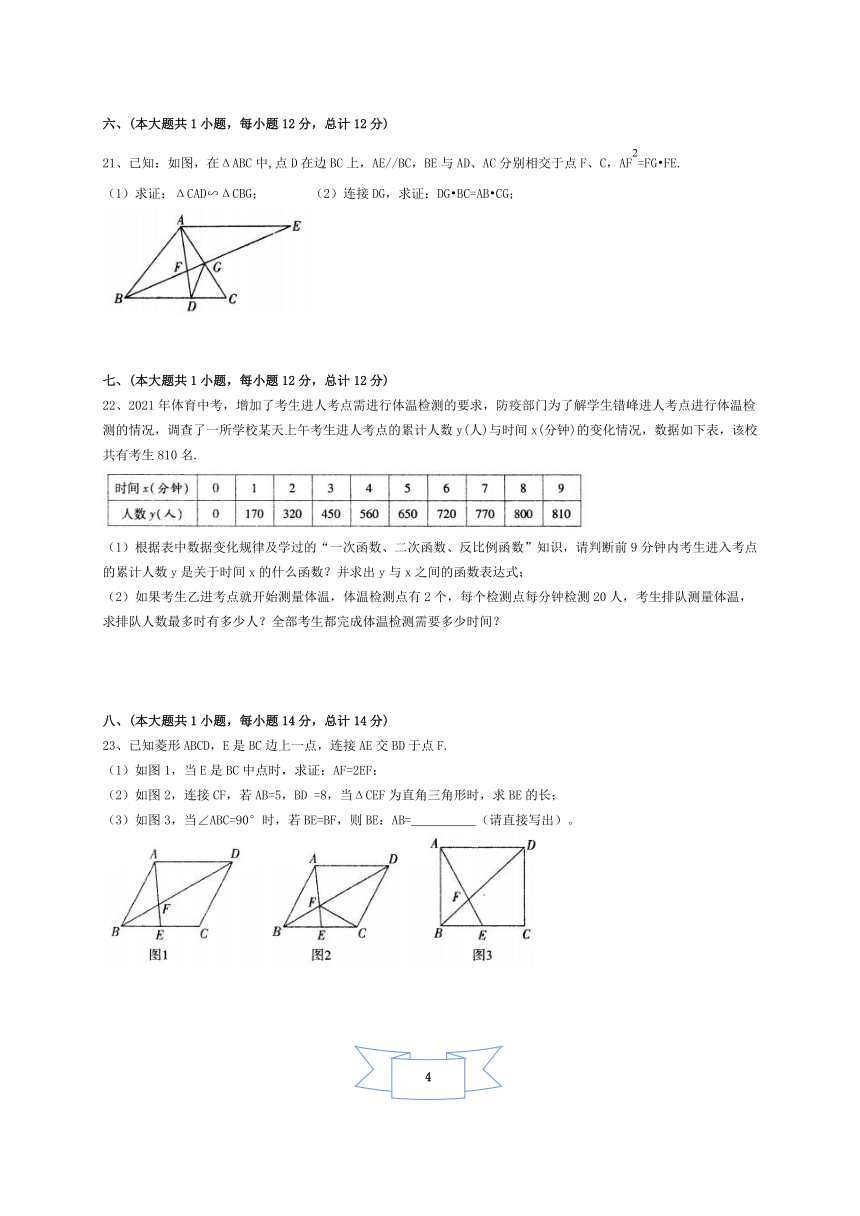
21、已知:如图,在ΔABC 中,点 D 在边 BC 上,AE//BC,BE 与 AD、AC分别相交于点 F、C,AF =FG FE.
(1)求证:ΔCAD∽ΔCBG; (2)连接 DG,求证:DG BC=AB CG;
七、(本大题共 1小题,每小题 12 分,总计 12 分)
22、2021 年体育中考,增加了考生进人考点需进行体温检测的要求,防疫部门为了解学生错峰进人考点进行体温检
测的情况,调查了一所学校某天上午考生进人考点的累计人数 y(人)与时间 x(分钟)的变化情况,数据如下表,该校
共有考生 810 名.
(1)根据表中数据变化规律及学过的“一次函数、二次函数、反比例函数”知识,请判断前 9 分钟内考生进入考点
的累计人数 y是关于时间 x的什么函数?并求出 y与 x之间的函数表达式;
(2)如果考生乙进考点就开始测量体温,体温检测点有 2个,每个检测点每分钟检测 20 人,考生排队测量体温,
求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
八、(本大题共 1小题,每小题 14 分,总计 14 分)
23、已知菱形 ABCD,E 是 BC边上一点,连接 AE 交 BD于点 F.
(1)如图 1,当 E 是 BC 中点时,求证:AF=2EF:
(2)如图 2,连接 CF,若 AB=5,BD =8,当ΔCEF 为直角三角形时,求 BE的长;
(3)如图 3,当∠ABC=90°时,若 BE=BF,则 BE:AB= (请直接写出)。
4
霍邱县 2021-2022 学年度第一学期期末考试
九年级数学试卷参考答案
一.选择题 :(本大题共 10 题,每小题 4分,满分 40 分)
1-5题:CCDDC 6-10 题: DBCBA
二、填空题(本大题共 4 题,每题 5 分,共 20 分)
4 1
11.﹣12; 12.(1,8); 13. ; 14.(1) (2分)(2)3 2 2
.(3分)
三.解答题(本大题共有 9 小题,共计 90 分)
15.解:原式 2 2
1
2 1 ………4分
2
= 4 …………8分
16.解:(1)如图所示:点 O即为所求(2分),
ABC与 A B C 的位似比是:1;2(2 分);
(2)如图所示:(4分)
17.解: AE // DF ,
BD BF 6 3
,即 ,
AD EF EF 2
EF 4, …………………………………………………………4分
BE BF EF 6 4 10,
DE // AC ,
BD BE 10 3
,即 ,
AD CE CE 2
CE 20 ,
3
FC CE 32 EF .……………………………………………………8分
3
18. 解:(1)如图, EF 为 AB的垂直平分线;
……………………………………………3分
第 1页,共 5页
(2)∵ EF 为 AB的垂直平分线
∴ AE 1 AB 5, AEF 90
2
∵在Rt ABC中, AC 8, AB 10
∴BC 102 82 6
∵ C AEF 90 , A A
∴ AFE∽ ABC
AE EF
∴ ,
AC BC
5 EF
即
8 6
15
∴ EF …………………………………………………………8 分
4
19.解:(1)第二小组的数据中,通过解直角三角形可得到△DBC中的 BC、DC,
无法与 Rt△ABH产生关联,故第二小组无法计算出河宽.………………4分
(2)答案不唯一.若选第一小组的方案及数据(如图),
∵∠ABH=∠ACH+∠BHC,∠ABH=70°,∠ACH=35°,
∴∠BHC=∠ACH=35°,
∴BH=BC=60m.
∴在 Rt△ABH中,AH=BH×sin70°≈56.4(m).………………………………10分
若选择第三小组方案及数据(如图),
AH
∵ =tan70o , AH =tan35o
AB AC
AB
∴ = 1 , AC = 1
AH tan 70o AH tan 35o
AB AC 1 1
∴ + = +
AH AH tan 70o tan 35o
BC
∴ = 1 + 1
AH tan 70o tan 35o
∵BC 101
AH 101∴
1 1
o tan70 tan35o
∵ tan 70 2.75,tan 35 0.70
∴ AH 56.4(m) ………………………………10分
第 2页,共 5页
20.解(1): y1 y2 ,…………………………………………………………2分
k k k k
∵ y1 , y , k 0 22 2 6 6
k k
∴
2 6
∴ y1 y2 …………………………………………………………4 分
(2)若选择条件①:
∵ A( 2, y1),∴OC 2
∵四边形 OCED的面积为 2
∴OD 1 …………………………………………………………7分
∴ y2 1
k
∴ B( 6,1)在反比例函数 y (k 0)的图象上
x
∴ k 6 …………………………………………………………10 分
若选择条件②:
∵ y k k1 , y2
2 6
∴ AE y1 y2=
k + k = k ………………… ………………………6 分
2 6 3
∵ A( 2, y1)、B( 6, y2)
∴ BE 4 …………………………………………………………8分
∵ BE 2AE
2k
∴4
3
∴ k 6 …………………………………………………………10 分
21.证明: (1) AF 2 FG FE.
AF EF
,且 AFG EFA,
FG AF
FAG∽ FEA,
FAG E,
AE // BC,
E EBC,
EBC FAG,且 ACD BCG,
CAD∽ CBG; …………………………………………………………7分
(2) CAD∽ CBG,
CA CD
,且 DCG ACB
CB CG
CDG∽ CAB,
DG CG
,
AB BC
DG BC AB CG.…………………………………………………………12 分
第 3页,共 5页
22.解:(1)根据随着自变量 x的增加,累计人数 y越来越大,且增加的越来越慢,且 x, y
均为非负数,可以判断前 9分钟内考生进入考点的累计人数 y 是关于时间 x的二次
函数(答案不唯一,只要能否定一次函数和反比例函数即可给分)。
∵当 x 0时, y 0,
∴二次函数的关系式可设为 y ax2 bx.
当 x 1时, y 170;当 x 3时, y 450 .
170 a b
将它们分别代入关系式得
450 9a 3b
a 10
解得 .
b 180
∴二次函数的表达式为 y 10x2 180x.…………………………………6 分
(2)设第 x分钟时的排队人数是W ,根据题意,得
y 10x2 180x
当0 x 9时, y 10x2 140x= 10(x 7)2 490
∴当 x 7时,W =490.…………………………………………………10 分
最大值
要全部考生都完成体温检测,根据题意,
得810 40x=0,
解得 x 20.25.
∴排队人数最多时是 490 人,全部考生都完成体温检测需要 20.25 分钟.……12 分
23.(本题满分 14分)
(1)证明: E 是 BC的中点,
BC 2BE,
四边形 ABCD是菱形,
AD BC 2BE, AD // BC ,
FAD FEB , FDA FBE ,
AFD∽ EFB,
AF AD
,
EF EB
AF 2BE
2,
EF BE
AF 2EF ;………………………………………………………………2分
(2)连接 AC交 BD于 O,如图,
四边形 ABCD是菱形, BD 8,
第 4页,共 5页
AC、BD互相平分,
OA 1 AC,OB
1
BD 4,
2 2
F 在 BD上,
FC FA,
在Rt ABO 中, AOB 90 , AB 5,
OA AB2 OB2 3,
AC 6,
AD // BC ,
EAD FEB, FDA FBE ,
FDA∽ FBE ,………………………………………………………4分
①当 FEC 90 时,在 ABC 中,
S 1 BC AE 1 ABC AC OB,2 2
AE AC OB 6 4 24 ,
BC 5 5
7
在Rt AEB 中, AEB 90 , BE AB2 AE2 ;5
………………………………………………………7分
②当 EFC 90 时,在Rt AFC 中, AFC 90 ,点 O是 AC的中点,
1
OF AC 3,
2
DF 4 3 7, BF 1,
FBE∽ FDA,
BE BF BE 1
,即 ,
AD DF 5 7
BE 5 ; ………………………………………………………10分
7
③ 点 E在 BC边上,
点 F在线段 OB上,故 ECF ECA 90 ,
故 ECF 90 这种情况不存在,
7 5
综上所述,当 CEF 为直角三角形时,BE的长为 或 ;…………………12分
5 7
(3) 2 1.……………………………………………………………………………14分
第 5页,共 5页
温馨提示:本试卷内容沪科版九上全册第 21 章~23 章、共 4 页八大题、23小题,满分 150 分,时间 120 分钟
一、选择题(本大题共 10 小题,每小题 4 分,满分 40 分)
1、已知 2x=3y(xy≠0),那么下列比例式中成立的是( )
x 2 x 3
A
x y x y
y 3 B
C D
2 3 3 2 2 y
2、将抛物线 y=x 向上平移 3 个单位长度,再向右平移 5 个单位长度,所得的抛物线为( )
A.y=(x+3) +5 B.y=(x-3) +5 C.y=(x-5) +3 D.y=(x+5) +3
3、若角 a的余角是 30°,则 cosa 的值是( )
3 3 2 1
A B C D
3 2 3 2
a2 1
4、已知点 A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数 y= (a 是常数)的图象上,且 y1 <y2<0<y3,x
则 x1、x2、x3 的大小关系为( )
A.x2>x1>x3 B.x1>x2>x3 C.x3>x2>x1 D.x3>x1>x2
k
5、在同一平面直角坐标系中,一次函数 y1=k1x+b 与反比例函数 y2=
2 (x>0)的图象如图所示,则当 y >y 时,自
x 1 2
变量 x的取值范围为( )
A.0<x<l B.x>3 C.1<x<3 D.x<1
第 5题图 第 6题图 第 7题图 第 8题图 第 9题图
6、生活中到处可见黄金分割的美,如上图,在设计人体雕像时,使雕像的腰部以下 a与全身 b的高度比值接近 0. 618,
可以增加视觉美感,若图中 b为 2米,则 a约为( )
A.1.52 米 B.1.38 米 C.1.42 米 D.1.24 米.
7、如图,某停车场入口的栏杆 AB ,从水平位置绕点 0 旋转到 A'B'的位置,已知 AO 的长为 4米,若栏杆的旋转角
∠A0A' =α,则栏杆 A端升高的高度为( )
4 4
A 米 B 4sinα米 C 米 D cosα米
sin cos
k
8、如图,ΔABO 的顶点 A 在函数 y= (x>0)的图象上,∠ABO=90°,过 AO 边的三等分点 M、N分别作 x轴的平行
x
线交 AB于点 P、Q,若四边形 MNQP 的面积为 3,则 k的值为( )
A.9 B.12 C.18 D.15
9、如图,在ΔABC 中,点 D 在 BC 上,连接 AD,点 E在 AC 上,过点 E作 EF//BC,交 AD 于点 F,过点 E作 EC//AB,
交 BC于点 G,则下列式子一定正确的是( )
A AE:EC=EF:CD B AF:FD=BG:GC C EG:AB=EF:CD D CG:BC=AF:AD
1
10、如图,正ΔABC 的边长为 4,点 P为 BC 边上的任意一点(不与点 B、C重合),且∠APD=60°,PD 交 AB 于点 D,
设 BP=x,BD=y,则 y 关于 x 的函数图象大致是( )
A B C D
二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)
k
11、已知反比例函数 y= 的图象经过点( -3,4),则 k的值是
x
12、抛物线 y=3(x-1) +8 的顶点坐标为
13、如图,矩形 ABCD 中,AB=2,E 为 CD 的中点,连接 AE、BD 交于点 P,过点 P作 PQ⊥BC于点 Q,则 PQ=
第 13 题图 第 14题图
14、如图,在 RtΔABC 中,∠ACB=90°,0为 AB 的中点,0D平分∠AOC 交 AC 于点 G,0D =0A,BD 分别与 AC,0C 交
于点 E、F,连接 AD、CD,则 OG:BC 的值为 ;若 CE=CF,则 CF:OF 的值为
三、(本大题共 2小题,每小题 8分,总计 16 分)
15、计算: 3 8 2 2cos600 (3.14 ) 0
16、如图,在边长为 1个单位长度的小正方形组戒的网格中,△ABC 与△A'B'C'以点 0 为位似中心,且它们的顶点都
为网格线的交点
(1)在图中画出点 0(要保留画图痕迹),并直接写出:△ABC 与△A'B'C'的位似比是
(2)请在此网格中,以点 C为位似中心,再画一个△A1B1C2,使它与△ABC 的位似比等于 2:1
四、(本大题共 2小题,每小题 8分,总计 16 分)
17、如图,在ΔABC 中,D、E、F分别是 AB、BC 上的点,且 DE//AC、AE//DF,BD:AD=3:2,求 EF 和 FC 的长.
2
18、(1)用尺规作图作 AB 的垂直平分线 EF,交 AB 于点 E,交 AC 于点 F(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求 EF的长度;
五、(本大题共 2小题,每小题 10 分,总计 20 分)
19、为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案他们在河南岸的点 A处测得河北岸的
树 H恰好在 A的正北方向测量方案与数据如下表:
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到 0.1m,参考数据:sin70°≈0.94,sin35°≈0. 57,tan70°
≈2.75,tan35°≈0.70)
k
20、如图,点 A(-2,y1)、B(-6,y2)在反比例函数 y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为 C、D,x
AC 与 BD 相交于点 E
(1)根据图象直接写出 y1、y2 的大小关系,并通过计算加以验证;
(2)结合以上信息,从①四边形 OCED 的面积为 2;②BE=2AE 这两个条件中任选一个作为补充条件,求 k的值;
你选择的条件是_ (只填序号)
3
六、(本大题共 1小题,每小题 12 分,总计 12 分)
21、已知:如图,在ΔABC 中,点 D 在边 BC 上,AE//BC,BE 与 AD、AC分别相交于点 F、C,AF =FG FE.
(1)求证:ΔCAD∽ΔCBG; (2)连接 DG,求证:DG BC=AB CG;
七、(本大题共 1小题,每小题 12 分,总计 12 分)
22、2021 年体育中考,增加了考生进人考点需进行体温检测的要求,防疫部门为了解学生错峰进人考点进行体温检
测的情况,调查了一所学校某天上午考生进人考点的累计人数 y(人)与时间 x(分钟)的变化情况,数据如下表,该校
共有考生 810 名.
(1)根据表中数据变化规律及学过的“一次函数、二次函数、反比例函数”知识,请判断前 9 分钟内考生进入考点
的累计人数 y是关于时间 x的什么函数?并求出 y与 x之间的函数表达式;
(2)如果考生乙进考点就开始测量体温,体温检测点有 2个,每个检测点每分钟检测 20 人,考生排队测量体温,
求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
八、(本大题共 1小题,每小题 14 分,总计 14 分)
23、已知菱形 ABCD,E 是 BC边上一点,连接 AE 交 BD于点 F.
(1)如图 1,当 E 是 BC 中点时,求证:AF=2EF:
(2)如图 2,连接 CF,若 AB=5,BD =8,当ΔCEF 为直角三角形时,求 BE的长;
(3)如图 3,当∠ABC=90°时,若 BE=BF,则 BE:AB= (请直接写出)。
4
霍邱县 2021-2022 学年度第一学期期末考试
九年级数学试卷参考答案
一.选择题 :(本大题共 10 题,每小题 4分,满分 40 分)
1-5题:CCDDC 6-10 题: DBCBA
二、填空题(本大题共 4 题,每题 5 分,共 20 分)
4 1
11.﹣12; 12.(1,8); 13. ; 14.(1) (2分)(2)3 2 2
.(3分)
三.解答题(本大题共有 9 小题,共计 90 分)
15.解:原式 2 2
1
2 1 ………4分
2
= 4 …………8分
16.解:(1)如图所示:点 O即为所求(2分),
ABC与 A B C 的位似比是:1;2(2 分);
(2)如图所示:(4分)
17.解: AE // DF ,
BD BF 6 3
,即 ,
AD EF EF 2
EF 4, …………………………………………………………4分
BE BF EF 6 4 10,
DE // AC ,
BD BE 10 3
,即 ,
AD CE CE 2
CE 20 ,
3
FC CE 32 EF .……………………………………………………8分
3
18. 解:(1)如图, EF 为 AB的垂直平分线;
……………………………………………3分
第 1页,共 5页
(2)∵ EF 为 AB的垂直平分线
∴ AE 1 AB 5, AEF 90
2
∵在Rt ABC中, AC 8, AB 10
∴BC 102 82 6
∵ C AEF 90 , A A
∴ AFE∽ ABC
AE EF
∴ ,
AC BC
5 EF
即
8 6
15
∴ EF …………………………………………………………8 分
4
19.解:(1)第二小组的数据中,通过解直角三角形可得到△DBC中的 BC、DC,
无法与 Rt△ABH产生关联,故第二小组无法计算出河宽.………………4分
(2)答案不唯一.若选第一小组的方案及数据(如图),
∵∠ABH=∠ACH+∠BHC,∠ABH=70°,∠ACH=35°,
∴∠BHC=∠ACH=35°,
∴BH=BC=60m.
∴在 Rt△ABH中,AH=BH×sin70°≈56.4(m).………………………………10分
若选择第三小组方案及数据(如图),
AH
∵ =tan70o , AH =tan35o
AB AC
AB
∴ = 1 , AC = 1
AH tan 70o AH tan 35o
AB AC 1 1
∴ + = +
AH AH tan 70o tan 35o
BC
∴ = 1 + 1
AH tan 70o tan 35o
∵BC 101
AH 101∴
1 1
o tan70 tan35o
∵ tan 70 2.75,tan 35 0.70
∴ AH 56.4(m) ………………………………10分
第 2页,共 5页
20.解(1): y1 y2 ,…………………………………………………………2分
k k k k
∵ y1 , y , k 0 22 2 6 6
k k
∴
2 6
∴ y1 y2 …………………………………………………………4 分
(2)若选择条件①:
∵ A( 2, y1),∴OC 2
∵四边形 OCED的面积为 2
∴OD 1 …………………………………………………………7分
∴ y2 1
k
∴ B( 6,1)在反比例函数 y (k 0)的图象上
x
∴ k 6 …………………………………………………………10 分
若选择条件②:
∵ y k k1 , y2
2 6
∴ AE y1 y2=
k + k = k ………………… ………………………6 分
2 6 3
∵ A( 2, y1)、B( 6, y2)
∴ BE 4 …………………………………………………………8分
∵ BE 2AE
2k
∴4
3
∴ k 6 …………………………………………………………10 分
21.证明: (1) AF 2 FG FE.
AF EF
,且 AFG EFA,
FG AF
FAG∽ FEA,
FAG E,
AE // BC,
E EBC,
EBC FAG,且 ACD BCG,
CAD∽ CBG; …………………………………………………………7分
(2) CAD∽ CBG,
CA CD
,且 DCG ACB
CB CG
CDG∽ CAB,
DG CG
,
AB BC
DG BC AB CG.…………………………………………………………12 分
第 3页,共 5页
22.解:(1)根据随着自变量 x的增加,累计人数 y越来越大,且增加的越来越慢,且 x, y
均为非负数,可以判断前 9分钟内考生进入考点的累计人数 y 是关于时间 x的二次
函数(答案不唯一,只要能否定一次函数和反比例函数即可给分)。
∵当 x 0时, y 0,
∴二次函数的关系式可设为 y ax2 bx.
当 x 1时, y 170;当 x 3时, y 450 .
170 a b
将它们分别代入关系式得
450 9a 3b
a 10
解得 .
b 180
∴二次函数的表达式为 y 10x2 180x.…………………………………6 分
(2)设第 x分钟时的排队人数是W ,根据题意,得
y 10x2 180x
当0 x 9时, y 10x2 140x= 10(x 7)2 490
∴当 x 7时,W =490.…………………………………………………10 分
最大值
要全部考生都完成体温检测,根据题意,
得810 40x=0,
解得 x 20.25.
∴排队人数最多时是 490 人,全部考生都完成体温检测需要 20.25 分钟.……12 分
23.(本题满分 14分)
(1)证明: E 是 BC的中点,
BC 2BE,
四边形 ABCD是菱形,
AD BC 2BE, AD // BC ,
FAD FEB , FDA FBE ,
AFD∽ EFB,
AF AD
,
EF EB
AF 2BE
2,
EF BE
AF 2EF ;………………………………………………………………2分
(2)连接 AC交 BD于 O,如图,
四边形 ABCD是菱形, BD 8,
第 4页,共 5页
AC、BD互相平分,
OA 1 AC,OB
1
BD 4,
2 2
F 在 BD上,
FC FA,
在Rt ABO 中, AOB 90 , AB 5,
OA AB2 OB2 3,
AC 6,
AD // BC ,
EAD FEB, FDA FBE ,
FDA∽ FBE ,………………………………………………………4分
①当 FEC 90 时,在 ABC 中,
S 1 BC AE 1 ABC AC OB,2 2
AE AC OB 6 4 24 ,
BC 5 5
7
在Rt AEB 中, AEB 90 , BE AB2 AE2 ;5
………………………………………………………7分
②当 EFC 90 时,在Rt AFC 中, AFC 90 ,点 O是 AC的中点,
1
OF AC 3,
2
DF 4 3 7, BF 1,
FBE∽ FDA,
BE BF BE 1
,即 ,
AD DF 5 7
BE 5 ; ………………………………………………………10分
7
③ 点 E在 BC边上,
点 F在线段 OB上,故 ECF ECA 90 ,
故 ECF 90 这种情况不存在,
7 5
综上所述,当 CEF 为直角三角形时,BE的长为 或 ;…………………12分
5 7
(3) 2 1.……………………………………………………………………………14分
第 5页,共 5页
同课章节目录
