2021-2022学年华东师大版七年级数学下册9.2多边形的内角和 教学设计
文档属性
| 名称 | 2021-2022学年华东师大版七年级数学下册9.2多边形的内角和 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 392.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 22:13:17 | ||
图片预览

文档简介
《多边形的内角和》教学设计
[教学目标]
经历探究多边形内角和计算方法的过程,培养学生的合作交流意识,同时培养学生善于发现、积极思考、勇于创新的学习态度。
[教学重点、难点]
教学重点:多边形的内角和的应用。
教学难点:探索多边形的内角和公式的过程。
[教学方法]
本节课采用“探究与互动”的教学方式。
[教学过程]
(一)复习回顾:
1、什么是多边形?
2、n边形的一个顶点可以引_____条对角线,将n边形分成了________个三角形。
想一想:
问题1:你还记得三角形内角和是多少度吗?
问题2:你知道长方形和正方形的内角和是多少?任意四边形的内角和也是360°吗?任意多边形的内角和是多少呢?
(二)引入新知:
试一试:
你会利用三角形的内角和计算四边形ABCD的内角和吗?
探究1:
1、从顶点A可以画几条对角线?
2、五边形被分成了几个三角形?
总结:
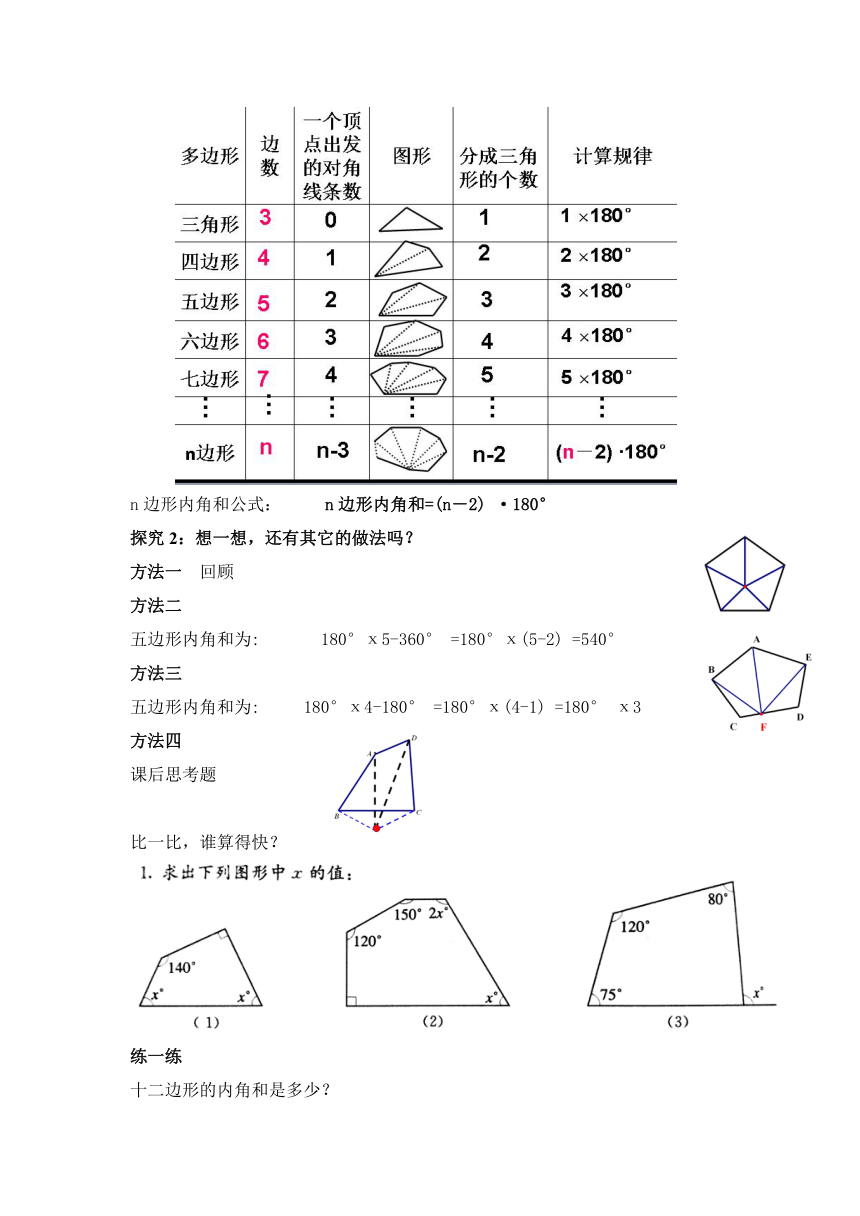
n边形内角和公式: n边形内角和=(n-2) ·180°
探究2:想一想,还有其它的做法吗?
方法一 回顾
方法二
五边形内角和为: 180°х5-360° =180°х(5-2) =540°
方法三
五边形内角和为: 180°х4-180° =180°х(4-1) =180° х3
方法四
课后思考题
比一比,谁算得快?
练一练
十二边形的内角和是多少?
(三)精讲点拨:
例1、一个多边形的内角和为2700°,求它的边数。
解 :设这是一个n边形,根据题意得:
(n-2)·180 °=2700 ° 解得: n=17
答:它的边数为17.
(四)拓展练习:
基础练习:
1、八边形的内角和等于 度;
九边形的内角和等于 度;
十边形的内角和等于 度
2、一个多边形的内角和等于720° 这个多边形是 边形.
开动脑筋:
1、 你能设计一个内角和是2014°的多边形吗?
2、如果一个多边形的边数增加1.则它的内角和将( )
A.增加90° B.增加180°
C.增加360° D.不变
挑战新高度:
1、若多边形的所有内角与它的一个外角的和为600°,则这个多边形是 边形这个外角的度数是 。
2、有一个四边形,截去一个角,所得多边形内角和是多少度?
(五)反思总结:
(1)n边形的内角和= (n-2)×180°
(2)n边形的外角和为360°
(3)几种数学思想:类比、转化、从特殊到一般、方程思想。
(六)布置作业:
必做题:习题11.3 第2、3.
选做题:
若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数是 ,这个多边形是 边形。
[教学目标]
经历探究多边形内角和计算方法的过程,培养学生的合作交流意识,同时培养学生善于发现、积极思考、勇于创新的学习态度。
[教学重点、难点]
教学重点:多边形的内角和的应用。
教学难点:探索多边形的内角和公式的过程。
[教学方法]
本节课采用“探究与互动”的教学方式。
[教学过程]
(一)复习回顾:
1、什么是多边形?
2、n边形的一个顶点可以引_____条对角线,将n边形分成了________个三角形。
想一想:
问题1:你还记得三角形内角和是多少度吗?
问题2:你知道长方形和正方形的内角和是多少?任意四边形的内角和也是360°吗?任意多边形的内角和是多少呢?
(二)引入新知:
试一试:
你会利用三角形的内角和计算四边形ABCD的内角和吗?
探究1:
1、从顶点A可以画几条对角线?
2、五边形被分成了几个三角形?
总结:
n边形内角和公式: n边形内角和=(n-2) ·180°
探究2:想一想,还有其它的做法吗?
方法一 回顾
方法二
五边形内角和为: 180°х5-360° =180°х(5-2) =540°
方法三
五边形内角和为: 180°х4-180° =180°х(4-1) =180° х3
方法四
课后思考题
比一比,谁算得快?
练一练
十二边形的内角和是多少?
(三)精讲点拨:
例1、一个多边形的内角和为2700°,求它的边数。
解 :设这是一个n边形,根据题意得:
(n-2)·180 °=2700 ° 解得: n=17
答:它的边数为17.
(四)拓展练习:
基础练习:
1、八边形的内角和等于 度;
九边形的内角和等于 度;
十边形的内角和等于 度
2、一个多边形的内角和等于720° 这个多边形是 边形.
开动脑筋:
1、 你能设计一个内角和是2014°的多边形吗?
2、如果一个多边形的边数增加1.则它的内角和将( )
A.增加90° B.增加180°
C.增加360° D.不变
挑战新高度:
1、若多边形的所有内角与它的一个外角的和为600°,则这个多边形是 边形这个外角的度数是 。
2、有一个四边形,截去一个角,所得多边形内角和是多少度?
(五)反思总结:
(1)n边形的内角和= (n-2)×180°
(2)n边形的外角和为360°
(3)几种数学思想:类比、转化、从特殊到一般、方程思想。
(六)布置作业:
必做题:习题11.3 第2、3.
选做题:
若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数是 ,这个多边形是 边形。
