2021-2022学年人教版数学八年级下册16.2.2二次根式的除法教案
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册16.2.2二次根式的除法教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 223.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 00:00:00 | ||
图片预览

文档简介
二次根式的除法教案
教学目标
1.知识与技能
(1)理解 =(a≥0,b>0),和=(a≥0,b>0);
(2)运用=(a≥0,b>0),和=(a≥0,b>0)进行运算.
2.过程与方法
(1)先由具体数据,发现规律,导出=(a≥0,b>0)并运用它进行计算;
(2)再利用逆向思维,得出=(a≥0,b>0)并运用它进行解题和化简.
(3)最后综合运用以上两个规律进行解题.
3.情感、态度与价值观
学生通过探究=(a≥0,b>0))培养学生由特殊到一般的探究精神;让学生推导=(a≥0,b>0)以训练逆向思维,通过严谨解题,增强学生准确解题的能力,引导学生从特殊到一般总结归纳的方法以及类比的方法,解决数学问题.
教学重难点
1.重点:理解=(a≥0,b>0),=(a≥0,b>0)及利用它们进行计算和化简.
2.难点:发现规律,归纳出二次根式的除法规定.
一.课堂导入
(学生活动)请同学们完成下列各题:
1.写出二次根式的乘法规定及逆向等式.
2.填空
(1)=________,=_________;
答案:;
(2)=________,=________;
答案:;
(3)=________,=_________;
答案:;
(4)=________,=________.
答案:;
规律:______;______;_______;
_______.
答案:都是等号;
3.利用计算器计算填空:
(1)=_________,(2)=_________,(3)=______,(4)=________.
规律:______;_______;_____;_____。
答案:都是等号;
每组推荐一名学生上台阐述运算结果.
二.探索新知
(老师点评) 刚才同学们都练习都很好,上台的同学也回答得十分准确,根据大家的练习和回答,我们可以得到:
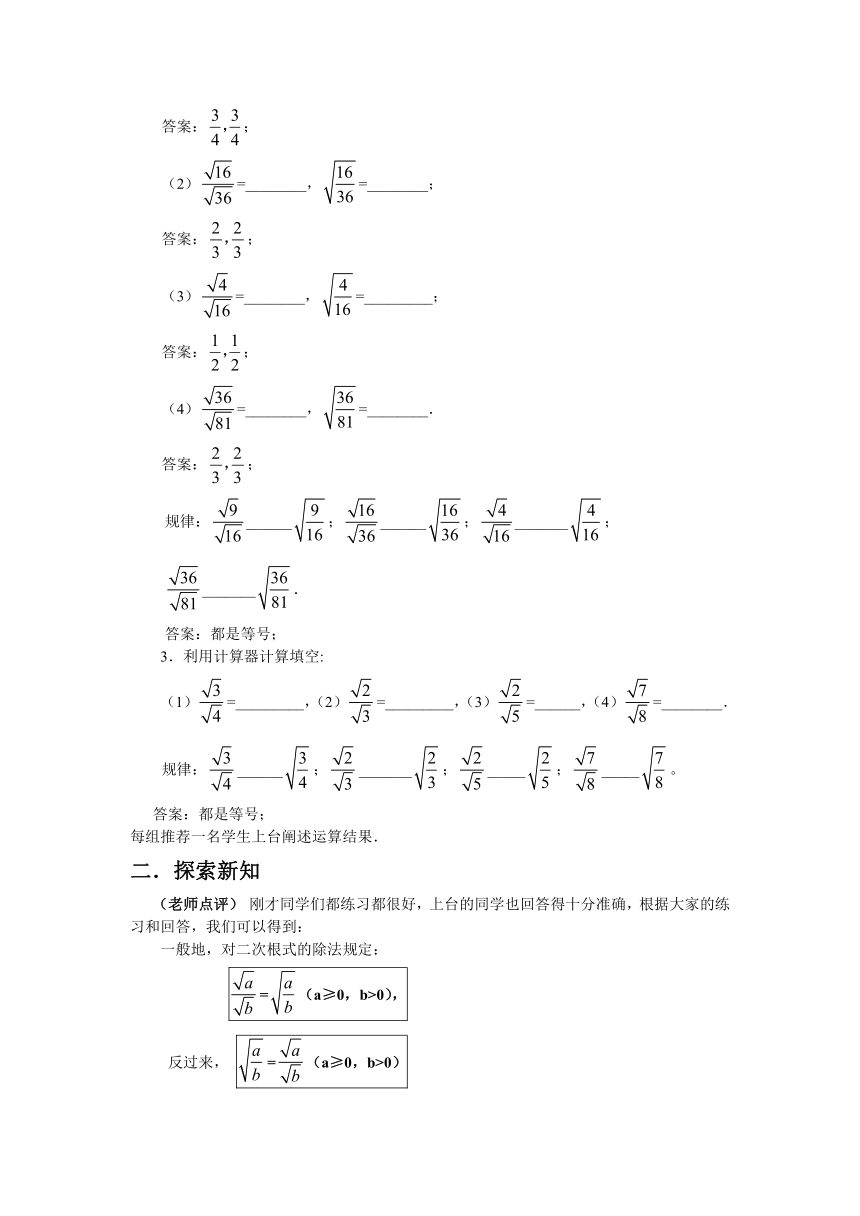
一般地,对二次根式的除法规定:
=(a≥0,b>0),
反过来, =(a≥0,b>0)
下面我们利用这个规定来计算和化简一些题目.
例1.计算:(1) (2) (3) (4)
分析:上面4小题利用=(a≥0,b>0)便可直接得出答案.
解:(1)===2
(2)==×=2
(3)===2
(4)===2
活动:自我检测
练习1 计算:
(1);
(2);
(3);
(4).
(找四名学生上黑板板演,其余学生在练习本上计算,然后再找学生指出不足.)
例2.化简:
(1) (2) (3) (4)
分析:直接利用=(a≥0,b>0)就可以达到化简之目的.
解:(1)=
(2)=
(3)=
(4)=
练习2 化简:
(1)
(2)
五、归纳小结
谈谈你的收获
1.商的算术平方根的性质 (注意公式成立的条件) .
2.会利用商的算术平方根的性质进行简单的二次根式的化简.
本节课要掌握=(a≥0,b>0)和=(a≥0,b>0)及其运用.
六、布置作业
作业:
计算:
(1);
(2);
(3) ;
(4) .
教学反思
(1)关键要利用具体数据,通过学生练习活动,发现规律,归纳出除法定律,并用逆向思维写出逆向等式及利用它们进行计算和化简.
(2)在计算和化简中要适时引入最简二次根式的概念,以规范做题。
教学目标
1.知识与技能
(1)理解 =(a≥0,b>0),和=(a≥0,b>0);
(2)运用=(a≥0,b>0),和=(a≥0,b>0)进行运算.
2.过程与方法
(1)先由具体数据,发现规律,导出=(a≥0,b>0)并运用它进行计算;
(2)再利用逆向思维,得出=(a≥0,b>0)并运用它进行解题和化简.
(3)最后综合运用以上两个规律进行解题.
3.情感、态度与价值观
学生通过探究=(a≥0,b>0))培养学生由特殊到一般的探究精神;让学生推导=(a≥0,b>0)以训练逆向思维,通过严谨解题,增强学生准确解题的能力,引导学生从特殊到一般总结归纳的方法以及类比的方法,解决数学问题.
教学重难点
1.重点:理解=(a≥0,b>0),=(a≥0,b>0)及利用它们进行计算和化简.
2.难点:发现规律,归纳出二次根式的除法规定.
一.课堂导入
(学生活动)请同学们完成下列各题:
1.写出二次根式的乘法规定及逆向等式.
2.填空
(1)=________,=_________;
答案:;
(2)=________,=________;
答案:;
(3)=________,=_________;
答案:;
(4)=________,=________.
答案:;
规律:______;______;_______;
_______.
答案:都是等号;
3.利用计算器计算填空:
(1)=_________,(2)=_________,(3)=______,(4)=________.
规律:______;_______;_____;_____。
答案:都是等号;
每组推荐一名学生上台阐述运算结果.
二.探索新知
(老师点评) 刚才同学们都练习都很好,上台的同学也回答得十分准确,根据大家的练习和回答,我们可以得到:
一般地,对二次根式的除法规定:
=(a≥0,b>0),
反过来, =(a≥0,b>0)
下面我们利用这个规定来计算和化简一些题目.
例1.计算:(1) (2) (3) (4)
分析:上面4小题利用=(a≥0,b>0)便可直接得出答案.
解:(1)===2
(2)==×=2
(3)===2
(4)===2
活动:自我检测
练习1 计算:
(1);
(2);
(3);
(4).
(找四名学生上黑板板演,其余学生在练习本上计算,然后再找学生指出不足.)
例2.化简:
(1) (2) (3) (4)
分析:直接利用=(a≥0,b>0)就可以达到化简之目的.
解:(1)=
(2)=
(3)=
(4)=
练习2 化简:
(1)
(2)
五、归纳小结
谈谈你的收获
1.商的算术平方根的性质 (注意公式成立的条件) .
2.会利用商的算术平方根的性质进行简单的二次根式的化简.
本节课要掌握=(a≥0,b>0)和=(a≥0,b>0)及其运用.
六、布置作业
作业:
计算:
(1);
(2);
(3) ;
(4) .
教学反思
(1)关键要利用具体数据,通过学生练习活动,发现规律,归纳出除法定律,并用逆向思维写出逆向等式及利用它们进行计算和化简.
(2)在计算和化简中要适时引入最简二次根式的概念,以规范做题。
