2021-2022学年人教版数学八年级下册16.3二次根式的加减 课件(共31张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册16.3二次根式的加减 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 569.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
16.3 二次根式的加减
人教版 · 数学· 八年级(下)
第十六章 二次根式
第1课时 二次根式的加减法运算
1.理解二次根式可以合并的条件。
2.类比整式的合并同类项,掌握二次根式的加减运算法则。
3.能熟练地进行二次根式的加减法运算。
学习目标
有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗?
导入新知
a
a
a
a
a
a
a
a
a
a
=
+
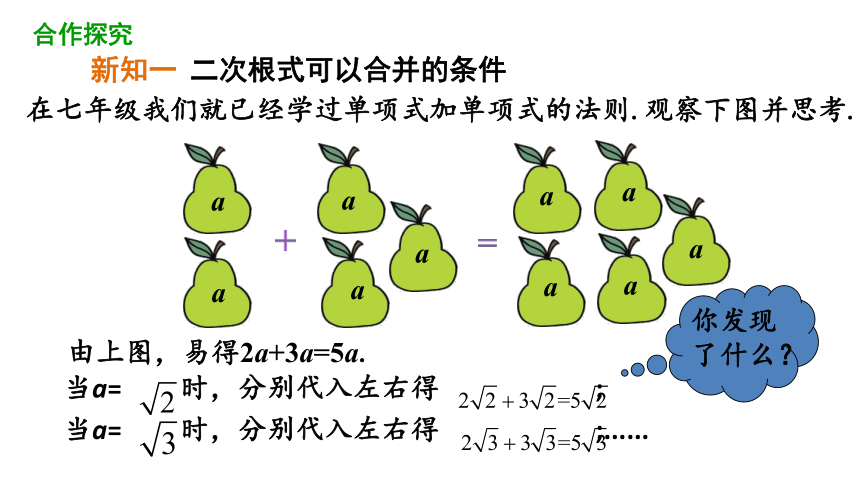
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得2a+3a=5a.
当a= 时,分别代入左右得 ;
当a= 时,分别代入左右得 ;......
新知一 二次根式可以合并的条件
你发现了什么?
合作探究
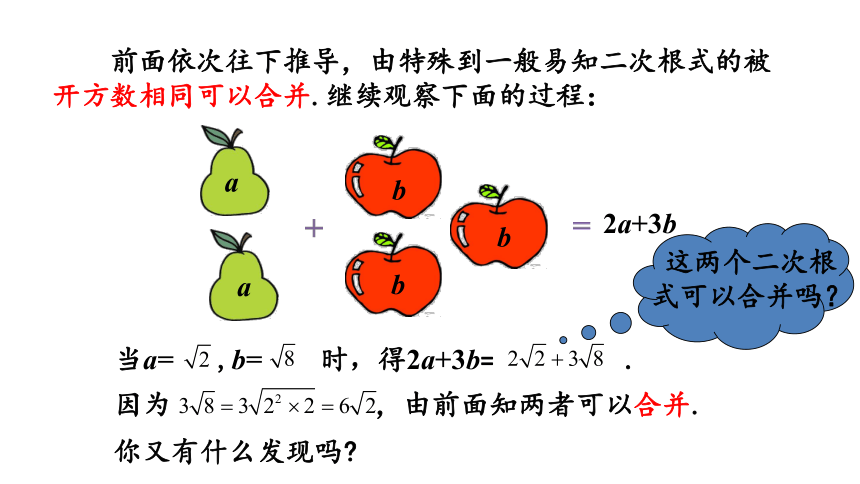
因为 ,由前面知两者可以合并.
当a= ,b= 时,得2a+3b= .
a
2a+3b
b
=
+
b
b
a
前面依次往下推导,由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程:
这两个二次根式可以合并吗?
你又有什么发现吗
将二次根式化成最简二次根式,如果被开方数相同,则这样的二次根式可以合并.
注意:1.判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断;
2.合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
归纳小结
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
2.下列二次根式,不能与 合并的是________(填 序号).
②
⑤
巩固新知
例 若最简二次根式 与 可以合并,求 的值.
解:由题意得
即
典例精析 利用二次根式可以合并的条件求字母的值
提示:可以合并的二次根式中字母取值的方法:利用被开方数相同,根指数都为2列关于字母的方程(组)求解即可.
解得
合作探究
1
(1) 与最简二次根式 能合并,则m =_____.
1
完成下列各题:
(2)若两个最简二次根式 与 可
以合并,则a=_____,b=_______.
1
巩固新知
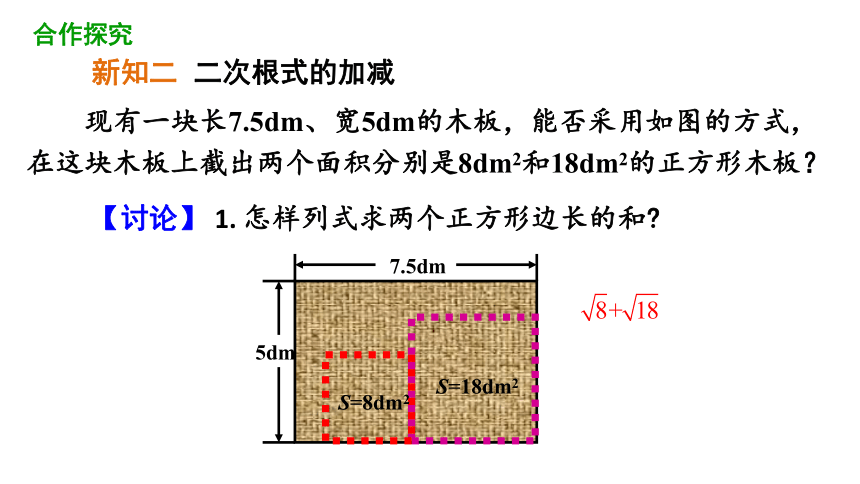
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
【讨论】 1. 怎样列式求两个正方形边长的和
S=8dm2
S=18dm2
新知二 二次根式的加减
合作探究
【讨论】2.所列算式能直接进行加减运算吗 如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
在有理数范围内成立的运算律,在实数范围内仍然成立.
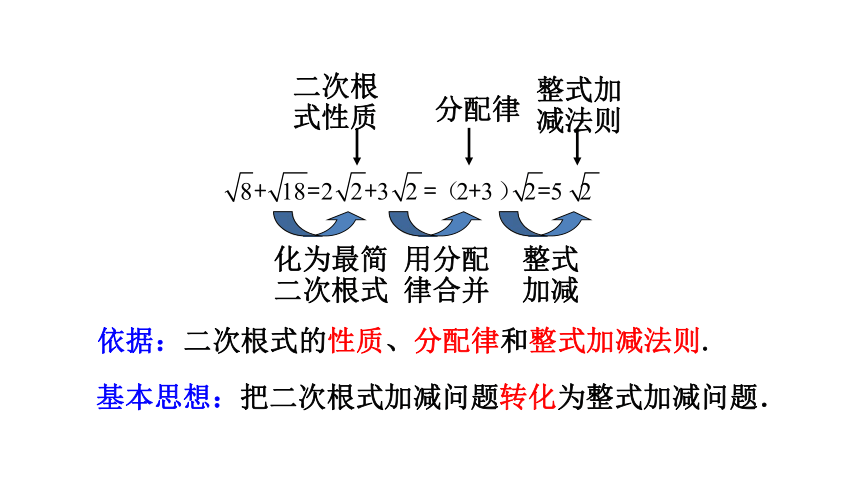
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
归纳小结
解:
例1 计算:
典例精析1 二次根式的加减计算
(1) ;
(3) ;
(4) .
(1)
(2) ;
(2)
(3)
(4)
合作探究
1.下列计算正确的是 ( )
A. B.
C. D.
C
2.已知一个矩形的长为 ,宽为 ,则其周长为______.
巩固新知
例2 计算:
解:
典例精析2 二次根式的加减混合运算
(1) ;
(2) .
(1)
(2)
计算时,有括号,一定要先去括号!
合作探究
解:原式
解:原式
计算:
(1) ;
(2) .
;
.
巩固新知
例3 有一个等腰三角形的两边长分别为 ,求其周长.
解:①当腰长为 时,
∵
∴此时能构成三角形,周长为
②当腰长为 时,
∵
∴此时能构成三角形,周长为
典例精析3 二次根式的综合性题目
合作探究
如图,两个圆的圆心相同,它们的面积分别是8cm2和18cm2,求圆环的宽度d(两圆半径之差).
解:
答:圆环的宽度d为 cm.
R-r
巩固新知
课堂练习
二次根式加减
法则
注意
运算顺序
运算原理
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
归纳新知
课后练习
再
见
16.3 二次根式的加减
人教版 · 数学· 八年级(下)
第十六章 二次根式
第1课时 二次根式的加减法运算
1.理解二次根式可以合并的条件。
2.类比整式的合并同类项,掌握二次根式的加减运算法则。
3.能熟练地进行二次根式的加减法运算。
学习目标
有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗?
导入新知
a
a
a
a
a
a
a
a
a
a
=
+
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得2a+3a=5a.
当a= 时,分别代入左右得 ;
当a= 时,分别代入左右得 ;......
新知一 二次根式可以合并的条件
你发现了什么?
合作探究
因为 ,由前面知两者可以合并.
当a= ,b= 时,得2a+3b= .
a
2a+3b
b
=
+
b
b
a
前面依次往下推导,由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程:
这两个二次根式可以合并吗?
你又有什么发现吗
将二次根式化成最简二次根式,如果被开方数相同,则这样的二次根式可以合并.
注意:1.判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断;
2.合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
归纳小结
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
2.下列二次根式,不能与 合并的是________(填 序号).
②
⑤
巩固新知
例 若最简二次根式 与 可以合并,求 的值.
解:由题意得
即
典例精析 利用二次根式可以合并的条件求字母的值
提示:可以合并的二次根式中字母取值的方法:利用被开方数相同,根指数都为2列关于字母的方程(组)求解即可.
解得
合作探究
1
(1) 与最简二次根式 能合并,则m =_____.
1
完成下列各题:
(2)若两个最简二次根式 与 可
以合并,则a=_____,b=_______.
1
巩固新知
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
【讨论】 1. 怎样列式求两个正方形边长的和
S=8dm2
S=18dm2
新知二 二次根式的加减
合作探究
【讨论】2.所列算式能直接进行加减运算吗 如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
在有理数范围内成立的运算律,在实数范围内仍然成立.
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
归纳小结
解:
例1 计算:
典例精析1 二次根式的加减计算
(1) ;
(3) ;
(4) .
(1)
(2) ;
(2)
(3)
(4)
合作探究
1.下列计算正确的是 ( )
A. B.
C. D.
C
2.已知一个矩形的长为 ,宽为 ,则其周长为______.
巩固新知
例2 计算:
解:
典例精析2 二次根式的加减混合运算
(1) ;
(2) .
(1)
(2)
计算时,有括号,一定要先去括号!
合作探究
解:原式
解:原式
计算:
(1) ;
(2) .
;
.
巩固新知
例3 有一个等腰三角形的两边长分别为 ,求其周长.
解:①当腰长为 时,
∵
∴此时能构成三角形,周长为
②当腰长为 时,
∵
∴此时能构成三角形,周长为
典例精析3 二次根式的综合性题目
合作探究
如图,两个圆的圆心相同,它们的面积分别是8cm2和18cm2,求圆环的宽度d(两圆半径之差).
解:
答:圆环的宽度d为 cm.
R-r
巩固新知
课堂练习
二次根式加减
法则
注意
运算顺序
运算原理
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
归纳新知
课后练习
再
见
