江苏省淮安市范集中学2012-2013学年高二上学期期中考试数学试题
文档属性
| 名称 | 江苏省淮安市范集中学2012-2013学年高二上学期期中考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 176.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-21 00:00:00 | ||
图片预览


文档简介
范集中学2012-2013学年高二上学期期中考试数学试题
一、填空题: 本大题共14小题,每小题5分,共计70分. 请把答案直接填写在答题卡相应位置上.
1、由一个平面多边形沿某一方向平移形成的空间几何体叫做 ▲
2、经过两点(2,3),(4,5)的直线的倾斜角为 ▲
3、若点P直线, 则由点P和直线确定的平面的个数是 ▲
4、与直线的斜率相等,且经过点A(2,3)的直线方程为 ▲
5、在长方体A1B1C1D1-ABCD中,直线AB与直线B1C1的位置关系是 ▲
6、如果AC<0,BC>0,那么直线不通过第 ▲ 象限
7、若一个正三棱锥的高为10cm,底面边长为6cm,则这个正三棱锥的体积为 ▲
8、已知则过点的直线的斜率为 ▲
9、E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则AC与平面EFGH的位置关系是 ▲
10、直线过点,且与两条坐标轴围成一个等腰直角三角形,则直线的方程为 ▲
11、已知球O的半径为3,则球O的表面积为 ▲
12、直线 经过的定点为 ▲
13、设为两两不重合的平面,为两两不重合的直线,给出下列四个命题:
①若,,则;
②若,,则;
③若,,,,则;
④若,,,,则。
其中命题正确的是 ▲ .(填序号)
14、一个直角梯形上底、下底和高之比是1:2:。将此直角梯形以垂直于底的腰旋转一周形成一个圆台,则这个圆台上底面积、下底面积和侧面积的比是 ▲
二、解答题: 本大题共6小题, 15-17每题14分,18-20每题16分,共计90分. 请在答题卡指定的区域
内作答, 解答时应写出文字说明,证明过程或演算步骤.
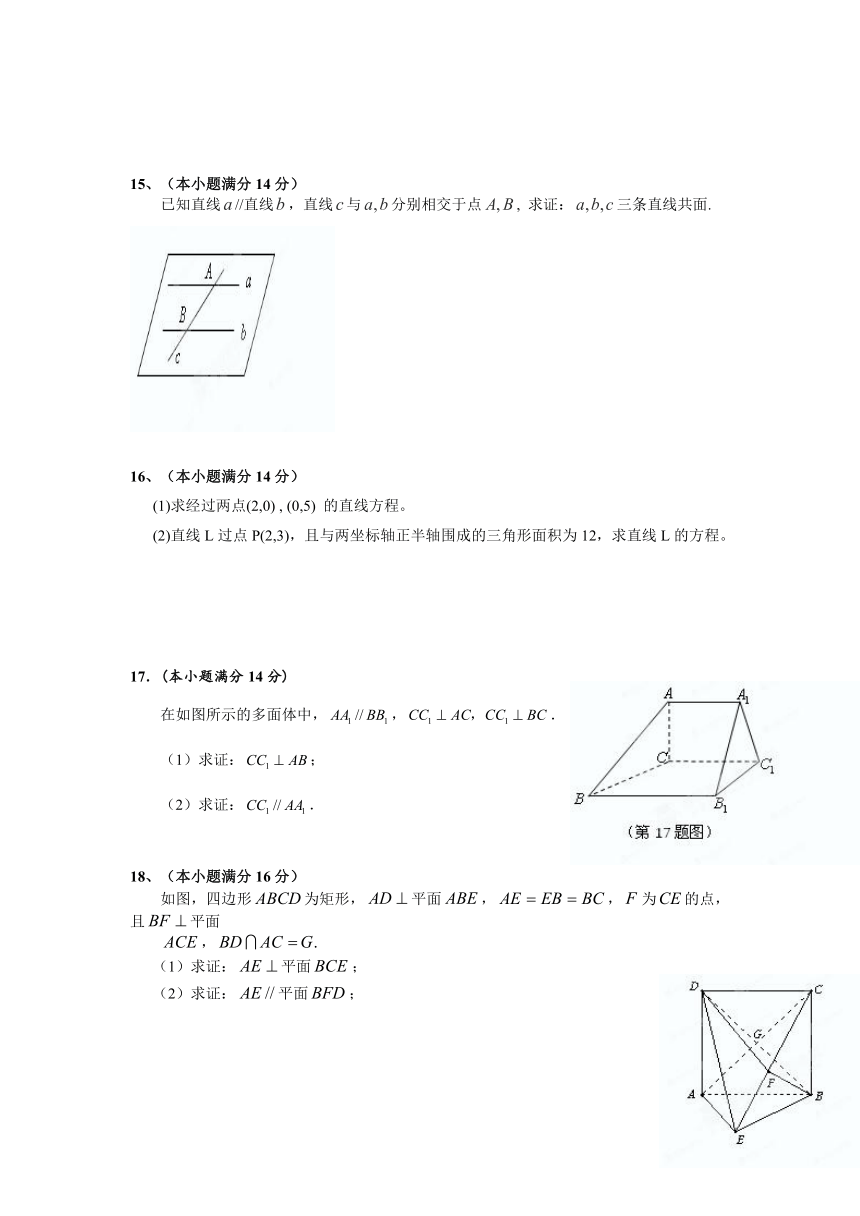
15、(本小题满分14分)
已知直线//直线,直线与分别相交于点, 求证:三条直线共面.
16、(本小题满分14分)
(1)求经过两点(2,0) , (0,5) 的直线方程。
(2)直线L过点P(2,3),且与两坐标轴正半轴围成的三角形面积为12,求直线L的方程。
17.(本小题满分14分)
在如图所示的多面体中,,.
(1)求证:;
(2)求证:.
18、(本小题满分16分)
如图,四边形为矩形,平面,,为的点,且平面
,
(1)求证:平面;
(2)求证:平面;
19、(本小题满分16分)
某商品的市场需求量(万件)、市场供应量(万件)与市场价格x(元/件)分别近似的满足下
列关系:,,当时的市场价格称为市场平衡价格,此时的需求量称为
平衡需求量。
(1)求平衡价格和平衡需求量;
(2)若要使平衡需求量增加6万件,政府对每件商品应给予多少元补贴?
(3)求当每件商品征税6元时新的平衡价格?
20、(本小题满分16分)
如图,直三棱柱中,、分别是棱、的中点,点在棱上,已知,,.
(1)求证:平面;
(2)设点在棱上,当为何值时,
平面平面?
高二数学期中考试试卷参考答案
16、解:(1)由截距式方程得, 即……………6分
(2)设方程为: ……………8分
由题意得 ……10分 得 ……………12分
则直线方程为: 即……………………14分
(用直线方程的点斜式同样给分)
17.证明:(1)因为,, 又,平面,
所以平面, …………………………4分
而平面, 所以; ……………………………………………6分
(2)因为,
又平面,平面, 所以平面,……………10分
而平面,平面平面,
所以. ……………………………………………………………14分
18、证明:(1)∵平面,,
∴平面,∴.
又 ∵平面, ∴,
∵,∴ ……………………………………8分
(2)连结 ,∵平面, ∴
∵ , ∴为的中点;∵ 矩形中, 为中点,
∴ . ∵ , ∴平面. ………………16分
19.解:(1)解方程组…………………4分 得…………5分
答:平衡价格为50元/件,平衡需求量为30万件。…………6分
(2)设政府给予t元/件补贴,此时市场平衡价格(即消费者支付价格)为x元/件,则供货者实
际每件得到(x+t)元,…………………7分
依题意有…………………10分
解得 ……11分 答:政府对每件商品应给予9元的补贴。…………12分
(3)设每件商品征税6元时,市场平衡价格为x元/件,……………13分
则 得x=54元……………15分
答:当每件商品征税6元时,新的市场平衡价格为54元。……………16分
20、证明:(1)连接交于,连接.
因为CE,AD为△ABC中线,
所以O为△ABC的重心,
从而OF//C1E.…………………………………4分
OF面ADF,平面,
所以平面.………………………7分
(2)当BM=1时,平面平面.
在直三棱柱中,
由于平面ABC,BB1平面B1BCC1,所以平面B1BCC1平面ABC.
由于AB=AC,是中点,所以.又平面B1BCC1∩平面ABC=BC,
所以AD平面B1BCC1.
而CM平面B1BCC1,于是ADCM.………………………………………10分
因为BM =CD=1,BC= CF=2,所以≌,所以CMDF.……12分
DF与AD相交,所以CM平面.
CM平面CAM,所以平面平面.…………………………15分
当BM=1时,平面平面.………………………………16分
一、填空题: 本大题共14小题,每小题5分,共计70分. 请把答案直接填写在答题卡相应位置上.
1、由一个平面多边形沿某一方向平移形成的空间几何体叫做 ▲
2、经过两点(2,3),(4,5)的直线的倾斜角为 ▲
3、若点P直线, 则由点P和直线确定的平面的个数是 ▲
4、与直线的斜率相等,且经过点A(2,3)的直线方程为 ▲
5、在长方体A1B1C1D1-ABCD中,直线AB与直线B1C1的位置关系是 ▲
6、如果AC<0,BC>0,那么直线不通过第 ▲ 象限
7、若一个正三棱锥的高为10cm,底面边长为6cm,则这个正三棱锥的体积为 ▲
8、已知则过点的直线的斜率为 ▲
9、E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则AC与平面EFGH的位置关系是 ▲
10、直线过点,且与两条坐标轴围成一个等腰直角三角形,则直线的方程为 ▲
11、已知球O的半径为3,则球O的表面积为 ▲
12、直线 经过的定点为 ▲
13、设为两两不重合的平面,为两两不重合的直线,给出下列四个命题:
①若,,则;
②若,,则;
③若,,,,则;
④若,,,,则。
其中命题正确的是 ▲ .(填序号)
14、一个直角梯形上底、下底和高之比是1:2:。将此直角梯形以垂直于底的腰旋转一周形成一个圆台,则这个圆台上底面积、下底面积和侧面积的比是 ▲
二、解答题: 本大题共6小题, 15-17每题14分,18-20每题16分,共计90分. 请在答题卡指定的区域
内作答, 解答时应写出文字说明,证明过程或演算步骤.
15、(本小题满分14分)
已知直线//直线,直线与分别相交于点, 求证:三条直线共面.
16、(本小题满分14分)
(1)求经过两点(2,0) , (0,5) 的直线方程。
(2)直线L过点P(2,3),且与两坐标轴正半轴围成的三角形面积为12,求直线L的方程。
17.(本小题满分14分)
在如图所示的多面体中,,.
(1)求证:;
(2)求证:.
18、(本小题满分16分)
如图,四边形为矩形,平面,,为的点,且平面
,
(1)求证:平面;
(2)求证:平面;
19、(本小题满分16分)
某商品的市场需求量(万件)、市场供应量(万件)与市场价格x(元/件)分别近似的满足下
列关系:,,当时的市场价格称为市场平衡价格,此时的需求量称为
平衡需求量。
(1)求平衡价格和平衡需求量;
(2)若要使平衡需求量增加6万件,政府对每件商品应给予多少元补贴?
(3)求当每件商品征税6元时新的平衡价格?
20、(本小题满分16分)
如图,直三棱柱中,、分别是棱、的中点,点在棱上,已知,,.
(1)求证:平面;
(2)设点在棱上,当为何值时,
平面平面?
高二数学期中考试试卷参考答案
16、解:(1)由截距式方程得, 即……………6分
(2)设方程为: ……………8分
由题意得 ……10分 得 ……………12分
则直线方程为: 即……………………14分
(用直线方程的点斜式同样给分)
17.证明:(1)因为,, 又,平面,
所以平面, …………………………4分
而平面, 所以; ……………………………………………6分
(2)因为,
又平面,平面, 所以平面,……………10分
而平面,平面平面,
所以. ……………………………………………………………14分
18、证明:(1)∵平面,,
∴平面,∴.
又 ∵平面, ∴,
∵,∴ ……………………………………8分
(2)连结 ,∵平面, ∴
∵ , ∴为的中点;∵ 矩形中, 为中点,
∴ . ∵ , ∴平面. ………………16分
19.解:(1)解方程组…………………4分 得…………5分
答:平衡价格为50元/件,平衡需求量为30万件。…………6分
(2)设政府给予t元/件补贴,此时市场平衡价格(即消费者支付价格)为x元/件,则供货者实
际每件得到(x+t)元,…………………7分
依题意有…………………10分
解得 ……11分 答:政府对每件商品应给予9元的补贴。…………12分
(3)设每件商品征税6元时,市场平衡价格为x元/件,……………13分
则 得x=54元……………15分
答:当每件商品征税6元时,新的市场平衡价格为54元。……………16分
20、证明:(1)连接交于,连接.
因为CE,AD为△ABC中线,
所以O为△ABC的重心,
从而OF//C1E.…………………………………4分
OF面ADF,平面,
所以平面.………………………7分
(2)当BM=1时,平面平面.
在直三棱柱中,
由于平面ABC,BB1平面B1BCC1,所以平面B1BCC1平面ABC.
由于AB=AC,是中点,所以.又平面B1BCC1∩平面ABC=BC,
所以AD平面B1BCC1.
而CM平面B1BCC1,于是ADCM.………………………………………10分
因为BM =CD=1,BC= CF=2,所以≌,所以CMDF.……12分
DF与AD相交,所以CM平面.
CM平面CAM,所以平面平面.…………………………15分
当BM=1时,平面平面.………………………………16分
同课章节目录
