2021-2022学年湘教版数学七年级数学下册4.4平行线的性质和判定的综合应用 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学七年级数学下册4.4平行线的性质和判定的综合应用 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 974.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 11:27:31 | ||
图片预览






文档简介
(共17张PPT)
平行线的性质和判定
第4章 相交线与平行线
1.分清平行线的性质和判定.已知平行用性质,要证平行用判定.
2.能够综合运用平行线性质和判定解题.
快速浏览课本P86-P93,思考下列问题:(时间5分钟)
1、平行线的性质有哪些?
2、平行线的判定有哪些?
3、平行线的性质与判定的区别与联系
自学指导
1.平行线的性质
同位角
内错角
同旁内角
图形
已知
结论
理由
1
2
)
)
a
b
c
3
)
2
)
a
b
c
4
2
)
)
a
b
c
a//b
a//b
a//b
两直线平行
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
知识回顾
知识回顾
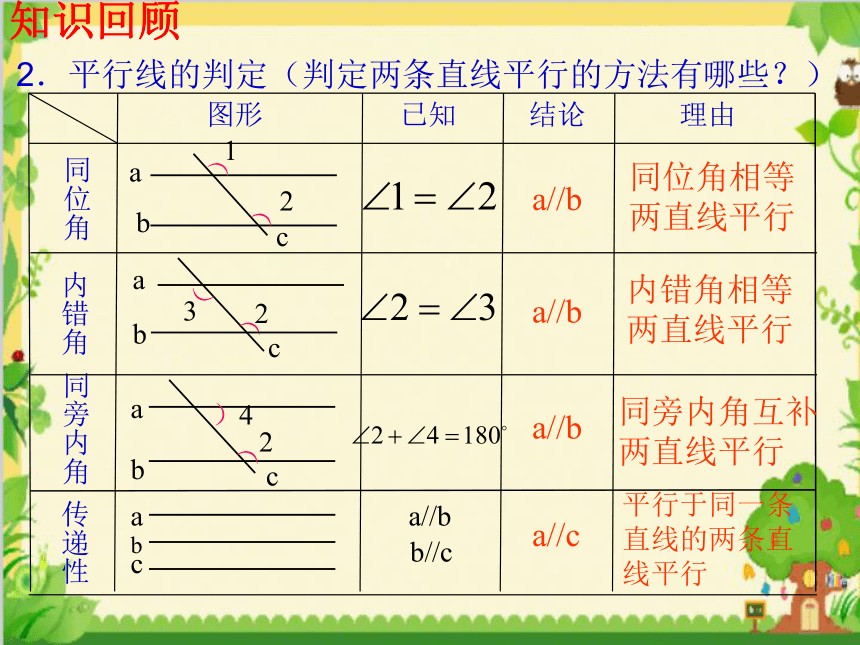
2.平行线的判定(判定两条直线平行的方法有哪些?)
同位角
内错角
同旁内角
传递性
图形
已知
结论
理由
1
2
)
)
a
b
c
3
)
2
)
a
b
c
4
2
)
)
a
b
c
c
b
a
a//b
b//c
a//b
a//b
a//b
a//c
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
平行于同一条直线的两条直线平行
平行线的性质与判定的区别与联系
(1)区别
性质是:根据两条直线平行,去证角的相等或互补.
判定是:根据两角相等或互补,去证两条直线平行.
(2)联系
它们都是以两条直线被第三条直线所截为前提;
它们的条件和结论是互逆的。
总结:已知平行用性质,要证平行用判定
自学检测
1. 下列说法:
①两条直线平行,同旁内角互补;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④垂直于同一直线的两直线平行。
其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④
2.如图1,直线a,b,c,d相交,则∠1=_____.
自学检测
3. 如图2,推理填空
①∵∠A=∠___(已知)
∴AC∥ED ( )
②∵∠2=∠___ (已知)
∴AC∥ED ( )
③∵∠A+∠____=180°(已知) ∴AB∥FD( )
④∵∠2+∠____=180°(已知)
∴AB∥FD ( )
自学检测
4. 如图3,AB∥EF,∠ECD=∠E,则CD∥AB.说理如下:
∵∠ECD=∠E
∴EF∥CD( )
又AB∥EF
∴CD∥AB( )
5、已知: 如图,∠1 = ∠2 = 55°,∠3等于多少度?
直线AB、CD平行吗? 说明你的理由.
3
1
2
A
B
F
C
D
E
一展身手
1. 如图4,已知:AB∥DE,∠ABC+∠DEF=180°, 求证:BC∥EF。
2. 如图5,已知:AB ∥CD,MG平∠AMN ,
NH平分∠DNM,求证:MG∥NH。
3. 如图6,已知:AD∥BC, ∠AEF=∠B,求证:AD∥EF。
.
挑战自我
1.如图7已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C..
2. 如图8,已知∠1=∠ACB,∠2=∠3,求证:CD∥HF.
3、如图:AD∥BC, ∠A=∠C.试说明AB∥DC
A
B
C
F
E
D
解:∵AD∥BC(已知)
∴∠C=∠CDE(两直线平行,内错角相等)
又∵ ∠A=∠C(已知)
∴ ∠A=∠CDE(等量代换)
∴AB∥DC(同位角相等,两直线平行)
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
(数量关系)
(位置关系)
(数量关系)
数形转化
平行线的判定与性质的关系图
证平行,用判定.
知平行,用性质.
课堂小结
必做题: 如图9,已知∠1=∠2,∠C=∠D,求证∠F=∠A
选做题:P95 6.
思考题:如图10,∠1:∠2:∠3=2:3:4,∠AFE=60°,
∠BDE=120°,写出图中平行的直线,并说明理由.
当堂训练
练习1 已知∠1= ∠2, ∠D+∠3=1800,
求证:EF//BC
证明: ∵ ∠1= ∠2
∴ AD// BC
∵ ∠D+∠3=1800
∴ AD// EF
∴ EF// BC
A
B
C
D
E
F
1
2
3
日日清
2、 如图,AB∥DE∥CF,∠B=70°,∠D=130°,
求∠BCD的度数.
解:∵AB∥CF,∠B=70°
∴∠BCF=∠B=70°
∵DE∥CF,∠D=130°
∴∠DCF=180°-∠D=180°-130°=50°
∴∠BCD=∠BCF-∠DCF=70°-50°=20°
平行线的性质和判定
第4章 相交线与平行线
1.分清平行线的性质和判定.已知平行用性质,要证平行用判定.
2.能够综合运用平行线性质和判定解题.
快速浏览课本P86-P93,思考下列问题:(时间5分钟)
1、平行线的性质有哪些?
2、平行线的判定有哪些?
3、平行线的性质与判定的区别与联系
自学指导
1.平行线的性质
同位角
内错角
同旁内角
图形
已知
结论
理由
1
2
)
)
a
b
c
3
)
2
)
a
b
c
4
2
)
)
a
b
c
a//b
a//b
a//b
两直线平行
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
知识回顾
知识回顾
2.平行线的判定(判定两条直线平行的方法有哪些?)
同位角
内错角
同旁内角
传递性
图形
已知
结论
理由
1
2
)
)
a
b
c
3
)
2
)
a
b
c
4
2
)
)
a
b
c
c
b
a
a//b
b//c
a//b
a//b
a//b
a//c
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
平行于同一条直线的两条直线平行
平行线的性质与判定的区别与联系
(1)区别
性质是:根据两条直线平行,去证角的相等或互补.
判定是:根据两角相等或互补,去证两条直线平行.
(2)联系
它们都是以两条直线被第三条直线所截为前提;
它们的条件和结论是互逆的。
总结:已知平行用性质,要证平行用判定
自学检测
1. 下列说法:
①两条直线平行,同旁内角互补;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④垂直于同一直线的两直线平行。
其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④
2.如图1,直线a,b,c,d相交,则∠1=_____.
自学检测
3. 如图2,推理填空
①∵∠A=∠___(已知)
∴AC∥ED ( )
②∵∠2=∠___ (已知)
∴AC∥ED ( )
③∵∠A+∠____=180°(已知) ∴AB∥FD( )
④∵∠2+∠____=180°(已知)
∴AB∥FD ( )
自学检测
4. 如图3,AB∥EF,∠ECD=∠E,则CD∥AB.说理如下:
∵∠ECD=∠E
∴EF∥CD( )
又AB∥EF
∴CD∥AB( )
5、已知: 如图,∠1 = ∠2 = 55°,∠3等于多少度?
直线AB、CD平行吗? 说明你的理由.
3
1
2
A
B
F
C
D
E
一展身手
1. 如图4,已知:AB∥DE,∠ABC+∠DEF=180°, 求证:BC∥EF。
2. 如图5,已知:AB ∥CD,MG平∠AMN ,
NH平分∠DNM,求证:MG∥NH。
3. 如图6,已知:AD∥BC, ∠AEF=∠B,求证:AD∥EF。
.
挑战自我
1.如图7已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C..
2. 如图8,已知∠1=∠ACB,∠2=∠3,求证:CD∥HF.
3、如图:AD∥BC, ∠A=∠C.试说明AB∥DC
A
B
C
F
E
D
解:∵AD∥BC(已知)
∴∠C=∠CDE(两直线平行,内错角相等)
又∵ ∠A=∠C(已知)
∴ ∠A=∠CDE(等量代换)
∴AB∥DC(同位角相等,两直线平行)
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
(数量关系)
(位置关系)
(数量关系)
数形转化
平行线的判定与性质的关系图
证平行,用判定.
知平行,用性质.
课堂小结
必做题: 如图9,已知∠1=∠2,∠C=∠D,求证∠F=∠A
选做题:P95 6.
思考题:如图10,∠1:∠2:∠3=2:3:4,∠AFE=60°,
∠BDE=120°,写出图中平行的直线,并说明理由.
当堂训练
练习1 已知∠1= ∠2, ∠D+∠3=1800,
求证:EF//BC
证明: ∵ ∠1= ∠2
∴ AD// BC
∵ ∠D+∠3=1800
∴ AD// EF
∴ EF// BC
A
B
C
D
E
F
1
2
3
日日清
2、 如图,AB∥DE∥CF,∠B=70°,∠D=130°,
求∠BCD的度数.
解:∵AB∥CF,∠B=70°
∴∠BCF=∠B=70°
∵DE∥CF,∠D=130°
∴∠DCF=180°-∠D=180°-130°=50°
∴∠BCD=∠BCF-∠DCF=70°-50°=20°
