任意角的三角函数
图片预览






文档简介
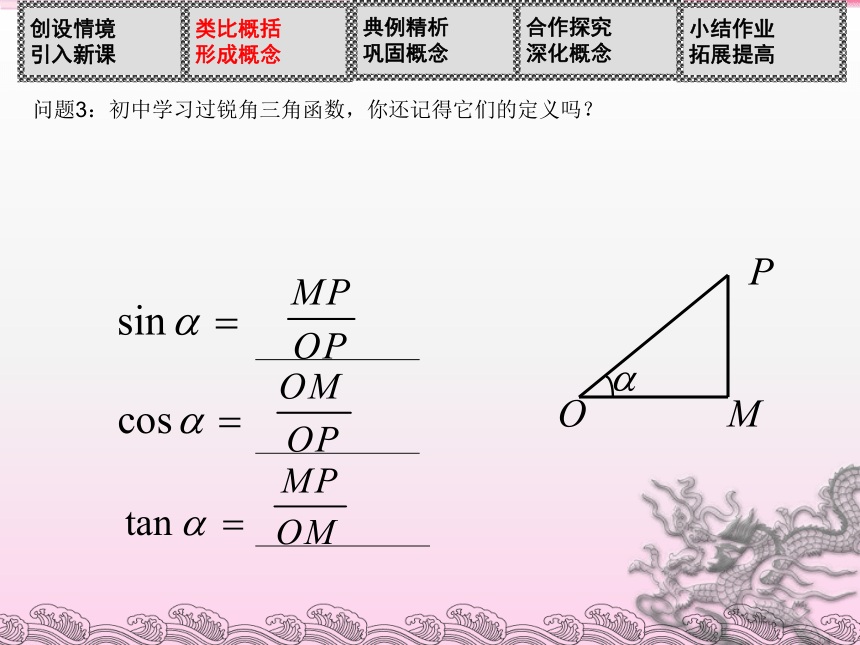
课件34张PPT。2.什么叫做1弧度的角?度与弧度是怎样换算的?(1)等于半径长的圆弧所对的圆心角叫做1弧度的角. 3. 与角α终边相同的角的一般表达式是什么?β=α+k·360°(k∈Z)或 (2)180°= rad.2019年2月6日星期三2人民教育出版社A版数学必修4第一章第二节第一课时任意角的三角函数 任意角是一条射线绕端点O旋转生成的.在旋转过程中,终边上的点都绕O点作着圆周运动. 问题1:任意角是怎样生成的?问题2:圆周运动体现了客观世界“周而复始”的变化规律,那么用什么函数刻画这种“周而复始”的变化规律呢?问题3:初中学习过锐角三角函数,你还记得它们的定义吗?问题3:初中学习过锐角三角函数,你还记得它们的定义吗?你能用直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗?
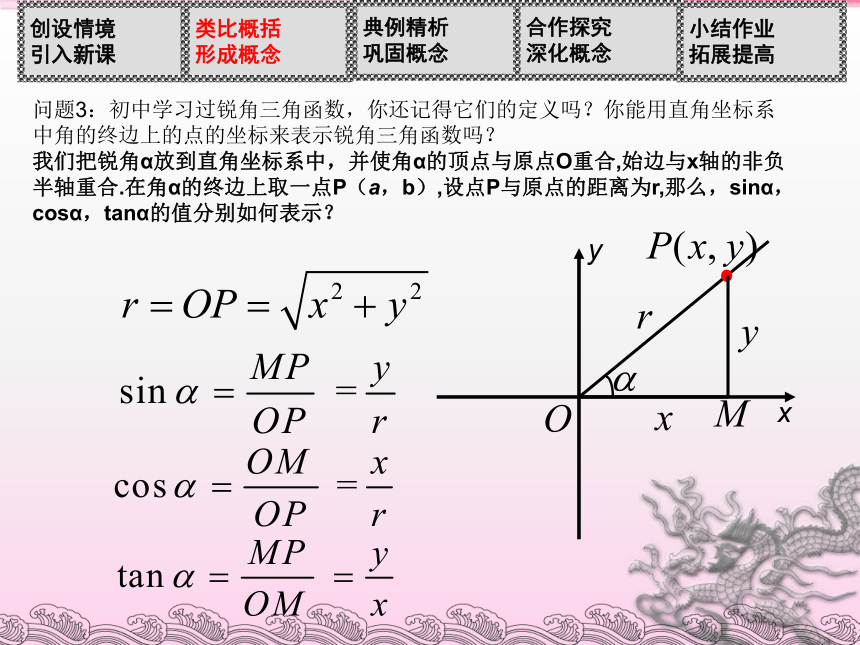
我们把锐角α放到直角坐标系中,并使角α的顶点与原点O重合,始边与x轴的非负半轴重合.在角α的终边上取一点P(a,b),设点P与原点的距离为r,那么,sinα,cosα,tanα的值分别如何表示?(2)对于锐角 的每一个确定的值 ,比值 都是确定的吗?上述三个比值是否随点P在角α的终边上的位置的改变而改变呢?为什么?
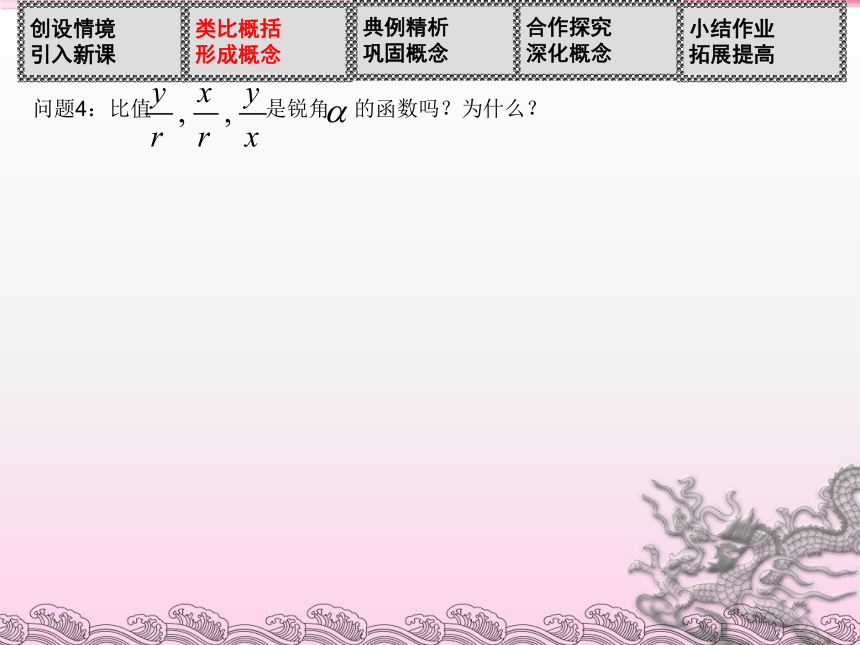
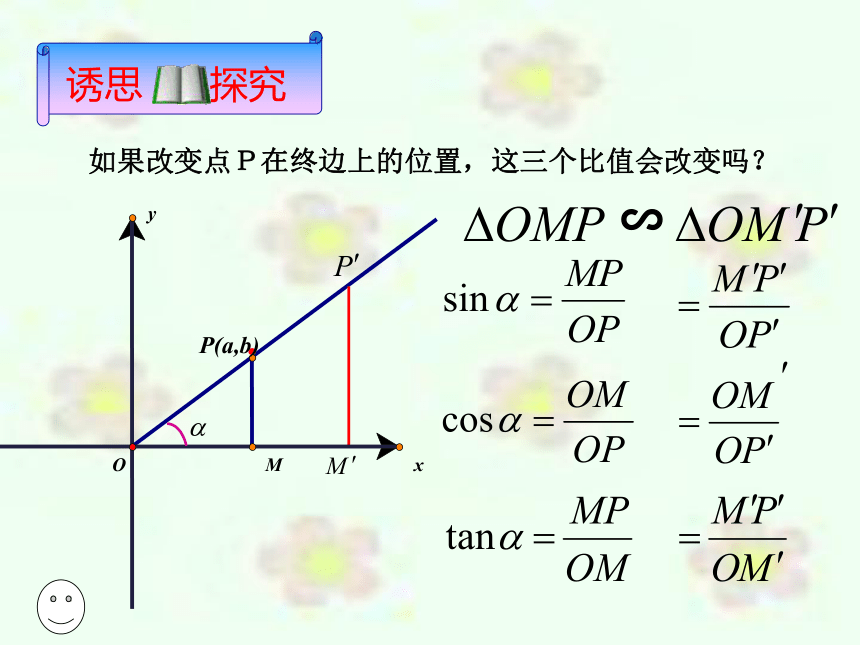
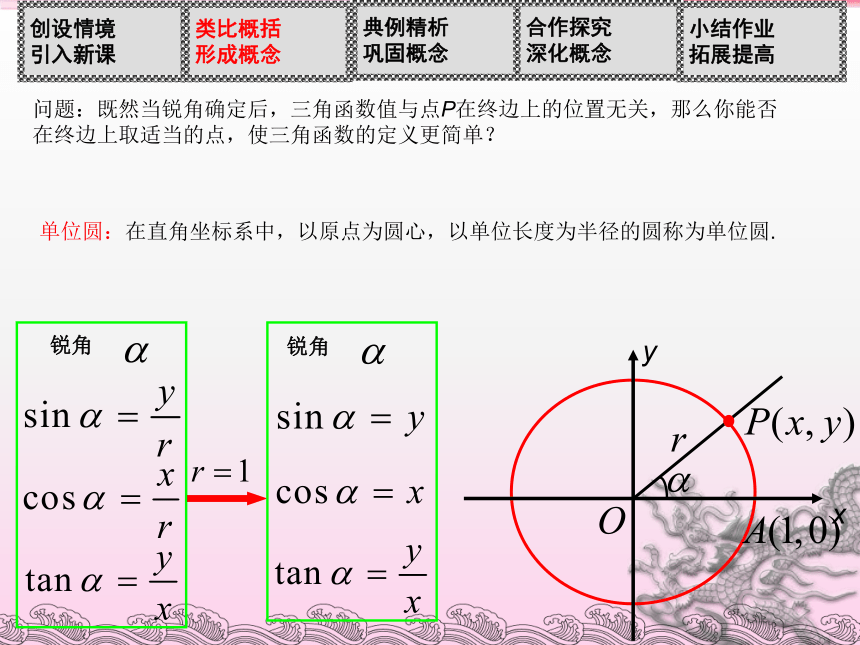
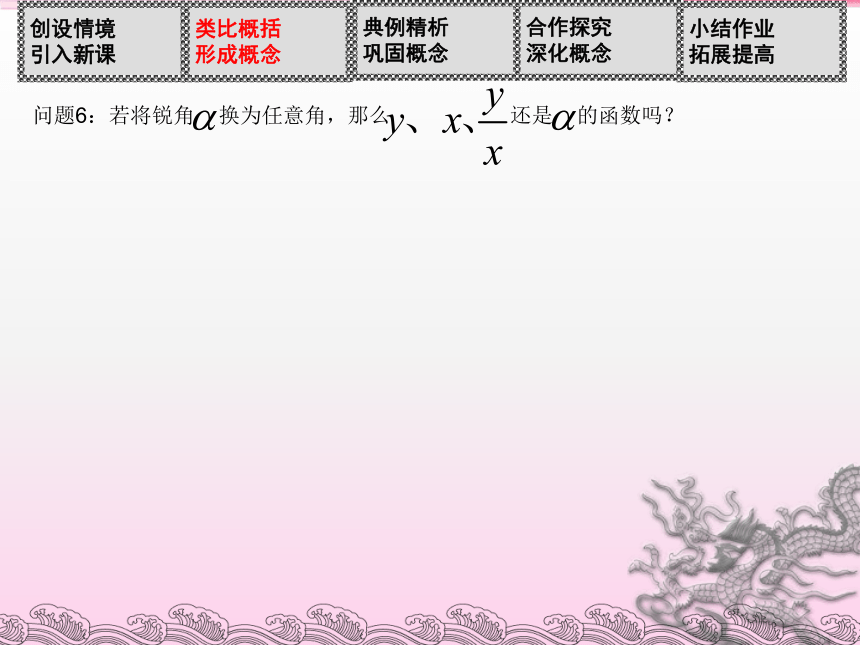
(1)当锐角 变化时,比值 会改变吗? 问题4:比值 是锐角 的函数吗?为什么?锐角问题4:比值 是锐角 的函数吗?为什么?如果改变点P在终边上的位置,这三个比值会改变吗?﹒∽MOyxP(a,b)思考3:为了使sinα,cosα的表示式更简单,你认为点P的位置选在何处最好?此时,sinα,cosα分别等于什么?问题:既然当锐角确定后,三角函数值与点P在终边上的位置无关,那么你能否在终边上取适当的点,使三角函数的定义更简单???????????????????? 单位圆:在直角坐标系中,以原点为圆心,以单位长度为半径的圆称为单位圆.问题6:若将锐角 换为任意角,那么 还是 的函数吗???????????????? 任意角的三角函数:如图,设? 是一个任意角,它的终边与单位圆交于点 ,那么:(1)纵坐标 叫做 的正弦,记作 ,即 ;(2)横坐标 叫做 的余弦,记作 ,即 ;(3)纵坐标与横坐标的比值 叫做 的正切,记作 ,即 .问题7:根据任意角的三角函数定义,确定它们在弧度制下的定义域.思考8:若点P(x,y)为角α终边上任意一点,那么sinα,cosα,tanα对应的函数值分别等于什么?
设角 是一个任意角, 是终边上的任意一点,
点 与原点的距离那么① 叫做 的正弦,即 ② 叫做 的余弦,即③ 叫做 的正弦,即 任意角 的三角函数值仅与 有关,而与点 在角的终边上的位置无关.补充定义:yx例1 求 的正弦、余弦和正切值.故 的终边与单位圆的交点坐标为小结:利用定义求三角函数值 ,关键是求出角的终边与单位圆交点的坐标.例3 已知角 的终边经过点 ,求角 的正弦、余弦和正切值 .解:由已知可得设角 的终边与单位圆交于 ,分别过点 、 作 轴的垂线 、\ 于是, 知识探究(二):三角函数符号与公式 思考2:设α是一个任意的象限角,那么当α在第一、二、三、四象限时,sinα的取值符号分别如何?cosα,tanα的取值符号分别如何?探究1.根据任意角的三角函数定义,确定三角函数值在各象限的符号.当角 满足不等式组 时,
角 为第 象限角.?????????????? 例2 全为+一全正二正弦三正切四余弦一、三角函数值的符号:规律: 例3 求证:当且仅当下列不等式组成立时,
角 为第三象限角.反之也对。① ②证明: 因为①式 成立,所以 角的终边可能位于第三 或第四象限,也可能位于y 轴的非正半轴上; 又因为②式 成立,所以角 的终边可能位于第一或第三象限. 因为①②式都成立,所以角 的终边只能位于第三象限.
于是角 为第三象限角.反过来请同学们自己证明.例4 确定下列三角函数值的符号:
(1) (2) (3)
解:(1)因为 是第三象限角,所以 ;(2)因为 = ,
而 是第一象限角,所以 ;练习 确定下列三角函数值的符号 (3)因为 是第四象限角,所以 .下列各式为正号的是( )
A cos2 B cos2?sin2
C tan2?cos2 D sin2?tan2C2 若lg(sin??tan?)有意义,则?是( )
A 第一象限角 B 第四象限角
C 第一象限角或第四象限角
D 第一或第四象限角或x轴的正半轴C3 已知?的终边过点(3a-9,a+2),且cos?<0,
sin?>0,则a的取值范围是 。-2的同一三角函数值有什么关系???????????????? 思考6:若sinα=sinβ,则角α与β的终边一定相同吗? 思考7:在求任意角的三角函数值时,上述公式有何功能作用?可将求任意角的三角函数值,转化为求0~ (或0°~360°)范围内的三角函数值. 思考8:函数的对应形式有一对一和多对一两种,三角函数是哪一种对应形式? 求下列三角函数值: (1);(2);(3)(2)(3)解:(1) 例3 特殊角的三角函数:不存在不存在小结作业1.三角函数都是以角为自变量,在弧度制中,三角函数的自变量与函数值都是在实数范围内取值.2.三角函数的定义是三角函数的理论基础,三角函数的定义域、函数值符号、公式一等,都是在此基础上推导出来的. 4.一个任意角的三角函数只与这个角的终边位置有关,与点P(x,y)在终边上的位置无关.公式一揭示了三角函数值呈周期性变化,即角的终边绕原点每旋转一周,函数值重复出现.3.若已知角α的一个三角函数符号,则角α所在的象限有两种可能;若已知角α的两个三角函数符号,则角α所在的象限就惟一确定.
我们把锐角α放到直角坐标系中,并使角α的顶点与原点O重合,始边与x轴的非负半轴重合.在角α的终边上取一点P(a,b),设点P与原点的距离为r,那么,sinα,cosα,tanα的值分别如何表示?(2)对于锐角 的每一个确定的值 ,比值 都是确定的吗?上述三个比值是否随点P在角α的终边上的位置的改变而改变呢?为什么?
(1)当锐角 变化时,比值 会改变吗? 问题4:比值 是锐角 的函数吗?为什么?锐角问题4:比值 是锐角 的函数吗?为什么?如果改变点P在终边上的位置,这三个比值会改变吗?﹒∽MOyxP(a,b)思考3:为了使sinα,cosα的表示式更简单,你认为点P的位置选在何处最好?此时,sinα,cosα分别等于什么?问题:既然当锐角确定后,三角函数值与点P在终边上的位置无关,那么你能否在终边上取适当的点,使三角函数的定义更简单???????????????????? 单位圆:在直角坐标系中,以原点为圆心,以单位长度为半径的圆称为单位圆.问题6:若将锐角 换为任意角,那么 还是 的函数吗???????????????? 任意角的三角函数:如图,设? 是一个任意角,它的终边与单位圆交于点 ,那么:(1)纵坐标 叫做 的正弦,记作 ,即 ;(2)横坐标 叫做 的余弦,记作 ,即 ;(3)纵坐标与横坐标的比值 叫做 的正切,记作 ,即 .问题7:根据任意角的三角函数定义,确定它们在弧度制下的定义域.思考8:若点P(x,y)为角α终边上任意一点,那么sinα,cosα,tanα对应的函数值分别等于什么?
设角 是一个任意角, 是终边上的任意一点,
点 与原点的距离那么① 叫做 的正弦,即 ② 叫做 的余弦,即③ 叫做 的正弦,即 任意角 的三角函数值仅与 有关,而与点 在角的终边上的位置无关.补充定义:yx例1 求 的正弦、余弦和正切值.故 的终边与单位圆的交点坐标为小结:利用定义求三角函数值 ,关键是求出角的终边与单位圆交点的坐标.例3 已知角 的终边经过点 ,求角 的正弦、余弦和正切值 .解:由已知可得设角 的终边与单位圆交于 ,分别过点 、 作 轴的垂线 、\ 于是, 知识探究(二):三角函数符号与公式 思考2:设α是一个任意的象限角,那么当α在第一、二、三、四象限时,sinα的取值符号分别如何?cosα,tanα的取值符号分别如何?探究1.根据任意角的三角函数定义,确定三角函数值在各象限的符号.当角 满足不等式组 时,
角 为第 象限角.?????????????? 例2 全为+一全正二正弦三正切四余弦一、三角函数值的符号:规律: 例3 求证:当且仅当下列不等式组成立时,
角 为第三象限角.反之也对。① ②证明: 因为①式 成立,所以 角的终边可能位于第三 或第四象限,也可能位于y 轴的非正半轴上; 又因为②式 成立,所以角 的终边可能位于第一或第三象限. 因为①②式都成立,所以角 的终边只能位于第三象限.
于是角 为第三象限角.反过来请同学们自己证明.例4 确定下列三角函数值的符号:
(1) (2) (3)
解:(1)因为 是第三象限角,所以 ;(2)因为 = ,
而 是第一象限角,所以 ;练习 确定下列三角函数值的符号 (3)因为 是第四象限角,所以 .下列各式为正号的是( )
A cos2 B cos2?sin2
C tan2?cos2 D sin2?tan2C2 若lg(sin??tan?)有意义,则?是( )
A 第一象限角 B 第四象限角
C 第一象限角或第四象限角
D 第一或第四象限角或x轴的正半轴C3 已知?的终边过点(3a-9,a+2),且cos?<0,
sin?>0,则a的取值范围是 。-2
