人教版 数学六年级下册 抽屉原理(课件)(共16张PPT)
文档属性
| 名称 | 人教版 数学六年级下册 抽屉原理(课件)(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 616.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
抽屉原理
有3枝笔,2个杯子,把3枝笔放进2个杯子里,怎么放?有几种不同放法?
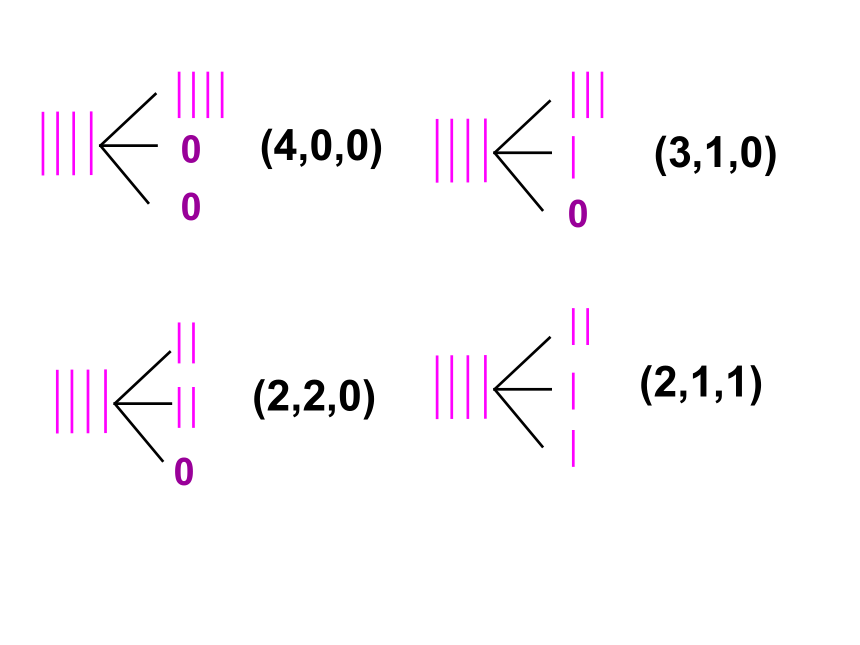
把4枝笔放进3个杯子里,怎么放?有几种不同放法?
0
0
(4,0,0)
0
(3,1,0)
(2,2,0)
0
(2,1,1)
不管怎么放,总有一个杯里至少有2枝笔.
把4枝笔放进3个杯子里,
把5枝笔放进4个杯子里,
把7枝笔放进6个杯子里,
把10枝笔放进9个杯子里,
不管怎么放,总有一个杯里至少放进2枝笔。
把100枝笔放进99个杯子里,
把3枝笔放进2个杯子里,
笔的枝数比杯子数多1,不管
怎么放,总有一个杯子里至少
放2枝笔。
物体数比抽屉数多1,不管怎么放,总有一个抽屉至少放2个物体。
把5本书放进2个抽屉中,不管怎么放,
总有一个抽屉至少放( )本?
把7本书放进2个抽屉中,不管怎么放,总有一个抽屉至少放( )本?
把9本书放进2个抽屉中,不管怎么放,总有一个抽屉至少放( )本?
物体的数量大于抽屉的数量,不管怎么放,总有一个抽屉里至少放进(商+1)个物体。
“抽屉原理”又称“鸽巢原理”,最先是由19世纪德国数学家狄利克雷提出来的,所以又称“狄利克雷原理”。
“抽屉原理”在解决实际问题中有着广泛的应用。“抽屉原理”的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
你知道吗?
做一做
7只鸽子飞回5个鸽笼,至少有2只鸽子要飞进同一个鸽笼里。为什么?
张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于9环。为什么?
41÷5=8(环) ……1(环)
8+1=9(环)
给一个正方体木块的6个面分别涂上蓝、黄两种颜色。不论怎么涂,至少有几个面涂的颜色相同,为什么?
6÷2=3(个)
计算小绝招
物体数÷抽屉数
至少数=商数+1
整除时 至少数=商
抽屉原理
有3枝笔,2个杯子,把3枝笔放进2个杯子里,怎么放?有几种不同放法?
把4枝笔放进3个杯子里,怎么放?有几种不同放法?
0
0
(4,0,0)
0
(3,1,0)
(2,2,0)
0
(2,1,1)
不管怎么放,总有一个杯里至少有2枝笔.
把4枝笔放进3个杯子里,
把5枝笔放进4个杯子里,
把7枝笔放进6个杯子里,
把10枝笔放进9个杯子里,
不管怎么放,总有一个杯里至少放进2枝笔。
把100枝笔放进99个杯子里,
把3枝笔放进2个杯子里,
笔的枝数比杯子数多1,不管
怎么放,总有一个杯子里至少
放2枝笔。
物体数比抽屉数多1,不管怎么放,总有一个抽屉至少放2个物体。
把5本书放进2个抽屉中,不管怎么放,
总有一个抽屉至少放( )本?
把7本书放进2个抽屉中,不管怎么放,总有一个抽屉至少放( )本?
把9本书放进2个抽屉中,不管怎么放,总有一个抽屉至少放( )本?
物体的数量大于抽屉的数量,不管怎么放,总有一个抽屉里至少放进(商+1)个物体。
“抽屉原理”又称“鸽巢原理”,最先是由19世纪德国数学家狄利克雷提出来的,所以又称“狄利克雷原理”。
“抽屉原理”在解决实际问题中有着广泛的应用。“抽屉原理”的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
你知道吗?
做一做
7只鸽子飞回5个鸽笼,至少有2只鸽子要飞进同一个鸽笼里。为什么?
张叔叔参加飞镖比赛,投了5镖,成绩是41环。张叔叔至少有一镖不低于9环。为什么?
41÷5=8(环) ……1(环)
8+1=9(环)
给一个正方体木块的6个面分别涂上蓝、黄两种颜色。不论怎么涂,至少有几个面涂的颜色相同,为什么?
6÷2=3(个)
计算小绝招
物体数÷抽屉数
至少数=商数+1
整除时 至少数=商
