安徽省合肥市第六十八中学2021-2022学年九年级上学期期末数学试卷(WORD版无答案)
文档属性
| 名称 | 安徽省合肥市第六十八中学2021-2022学年九年级上学期期末数学试卷(WORD版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 212.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-26 10:53:20 | ||
图片预览

文档简介
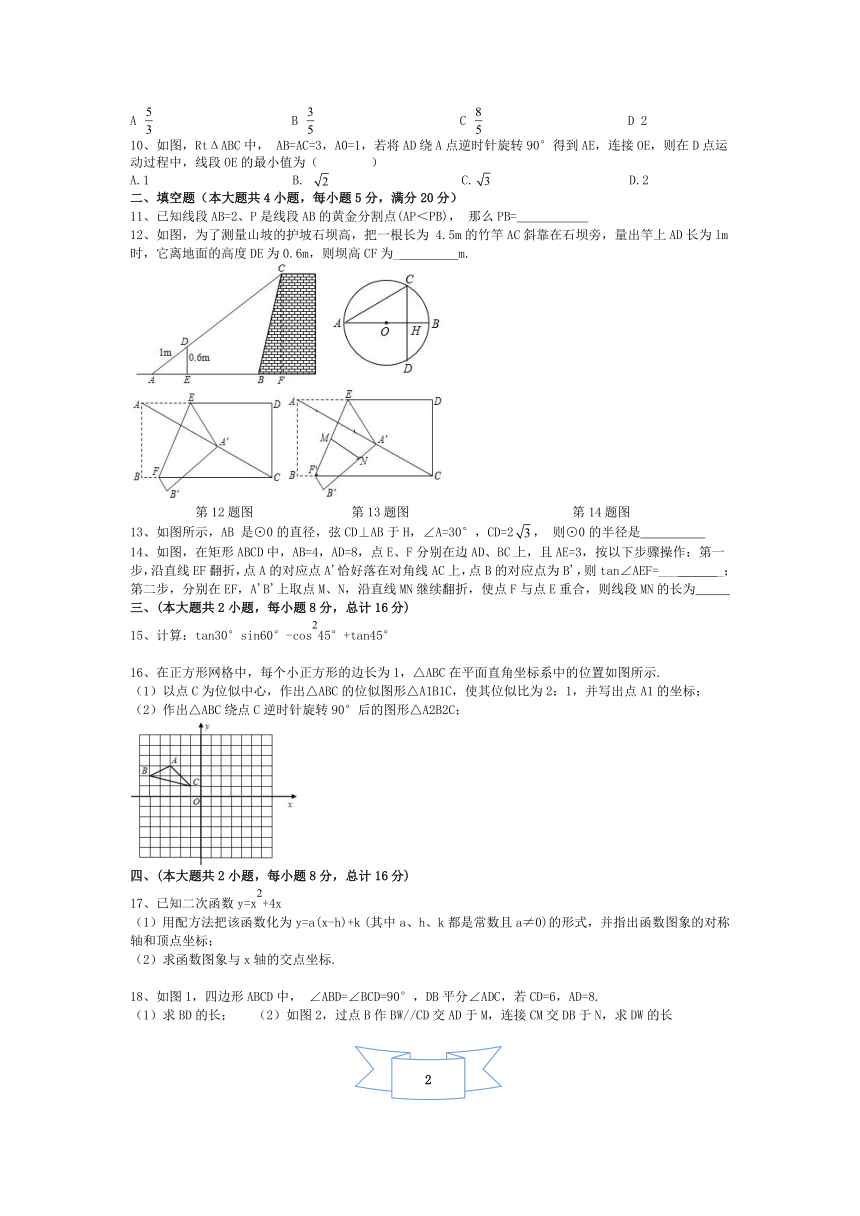
安徽省合肥市第六十八中学2021-2022学年九上期末数学试卷(原卷)
温馨提示:本试卷内容沪科版九上全册第21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1、剪纸艺术是第一批国家级非物质文化遗产,下列图案既是中心对称图形又是轴对称图形的是( )
A B C D
2、将抛物线y=2x向左平移3个单位长度,所得到新的抛物线的表达式为( )
A.y=2x-3 B. y=2x+3 C.y=2(x-3) D. y=2(x+3)
3、已知,则的值为( )
A - B C - D
4、如图,在4×5 的正方形网格中,每个小正方形的边长都是1,△ABC 的顶点都在这些小正方形的顶点上,那么cos∠ACB值为( )
A B C D
第4题图 第6题图 第7题图 第8题图 第9题图 第10题图
5、根据表格中二次函数y=ax+bx+c的自变量x与函数值y的对应值,可以判断方程ax+bx+c=0的一个解x的范
围是( )
x 0 0.5 1 1.5 2
y=ax+bx+c -1 -0.5 1 3.5 7
A 1.5<x<2 B 1<x<1.5 C 0.5<x<1 D 0<x<0.5
6、如图,点A是反比例函数y=(x>0)图象上任意-点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为( )
A.2 B.1 C.4 D.不能确定
7、以0为中心点的量角器与直角三角板ABC按如图方式摆放,量角器的0刻度线与斜边AB重合,点D为斜边AB上一点,作射线CD交弧AB于点E,如果点E所对应的读数为50°,那么∠BDE的大小为( )
A.100° B.110° C.115° D.130°
8、用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
9、如图,已知AD为ΔABC的角平分线,DE//AB交AC于E,如果AE:EC=3:5,那么AC:AB等于( )
A B C D 2
10、如图,RtΔABC中, AB=AC=3,A0=1,若将AD绕A点逆时针旋转90°得到AE,连接OE,则在D点运动过程中,线段OE的最小值为( )
A.1 B. C. D.2
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知线段AB=2、P是线段AB的黄金分割点(AP<PB), 那么PB=
12、如图,为了测量山坡的护坡石坝高,把一根长为 4.5m的竹竿AC斜靠在石坝旁,量出竿上AD长为lm时,它离地面的高度DE为0.6m,则坝高CF为_ m.
第12题图 第13题图 第14题图
13、如图所示,AB 是⊙0的直径,弦CD⊥AB于H,∠A=30°,CD=2, 则⊙0的半径是
14、如图,在矩形ABCD中,AB=4,AD=8,点E、F分别在边AD、BC上,且AE=3,按以下步骤操作:第一步,沿直线EF翻折,点A的对应点A'恰好落在对角线AC上,点B的对应点为B',则tan∠AEF=___ _;第二步,分别在EF,A'B'上取点M、N,沿直线MN继续翻折,使点F与点E重合,则线段MN的长为
三、(本大题共2小题,每小题8分,总计16分)
15、计算:tan30°sin60°-cos45°+tan45°
16、在正方形网格中,每个小正方形的边长为1,△ABC在平面直角坐标系中的位置如图所示.
(1)以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为2:1,并写出点A1的坐标;
(2)作出△ABC绕点C逆时针旋转90°后的图形△A2B2C;
四、(本大题共2小题,每小题8分,总计16分)
17、已知二次函数y=x+4x
(1)用配方法把该函数化为y=a(x-h)+k (其中a、h、k都是常数且a≠0)的形式,并指出函数图象的对称轴和顶点坐标;
(2)求函数图象与x轴的交点坐标.
18、如图1,四边形ABCD中, ∠ABD=∠BCD=90°,DB平分∠ADC,若CD=6,AD=8.
(1)求BD的长; (2)如图2,过点B作BW//CD交AD于M,连接CM交DB于N,求DW的长
五、(本大题共2小题,每小题10分,总计20分)
19、随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量翡翠湖某处东西岸边B, C两点之间的距离.如图所示,小星站在湖边的B处遥控无人机,无人机在A处距离地面的飞行高度是161.6m,此时从无人机测得岸边C处的俯角为63°,他抬头仰视无人机时,仰角为a,若小星的身高BE=1.6m, EA=200m(点A、E、B、C在同一平面内)
(1)求仰角a的正弦值;
(2)求B、C两点之间的距离(结果精确到1m)(sin63"≈0.89,cos63°≈0.45,tan63°≈1.96,sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
20、如图,AB是⊙0的切线,D点在⊙0上,AD与⊙0相交于C,CE是⊙0的直径,连接BC,若∠A=90°
(1)求证:CB平分∠ACE; (2)当AB=2,AC=1时,求⊙0的半径长
六、(本大题共1小题,每小题12分,总计12分)
21、如图,直线y1=k1x+b与双曲线在第一象限内交于A、B两点,已知A(1,m)、B(2,1)
(1)求k的值及直线AB的解析式;
(2)根据函数图象,直接写出不等式y1>y2的解集;
(3)设点P是线段AB上的一个动点, 过点P作PD⊥x轴于点D、E是y轴上一点,ΔPED的面积能否达到,
若能达到,请求出此时点P的坐标.
七、(本大题共1小题,每小题12分,总计12分)
22、某公司销售-种商品,成本为每件30元,经过市场调查发现,该商品的日销售量y (件)与销售单价x (元)是一次函数关系,其销售单价、日销售量的三组对应数值如下表:
销售单价x(元) 40 60 80
日销售量y 件) 80 60 40
(1)求公司销售该商品获得的最大日利润;
(2)销售一段时间以后,由于某种原因,该商品每件成本增加了10 元,若物价部门规定该商品销售单价不能超过a元,在日销售量y(件)与销售单价x (元)保持(1)中函数关系不变的情况下,该商品的日销售最大利润是1500元,求a的值.
八、(本大题共1小题,每小题14分,总计14分)
23、△ABC中,∠BAC=90°,AB=AC,D为BC的中点,F、E是AC上两点,连接BE、DF交于△ABC内一点G,且∠EGF=45°
(1)如图1,求证∠FDC=∠AEB;
(2)如图1,若AE=3CE=6,求BG的长:
(3)如图2,若F为AC上任意一点,连接AG,求证:∠EAG=∠ABE;
温馨提示:本试卷内容沪科版九上全册第21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1、剪纸艺术是第一批国家级非物质文化遗产,下列图案既是中心对称图形又是轴对称图形的是( )
A B C D
2、将抛物线y=2x向左平移3个单位长度,所得到新的抛物线的表达式为( )
A.y=2x-3 B. y=2x+3 C.y=2(x-3) D. y=2(x+3)
3、已知,则的值为( )
A - B C - D
4、如图,在4×5 的正方形网格中,每个小正方形的边长都是1,△ABC 的顶点都在这些小正方形的顶点上,那么cos∠ACB值为( )
A B C D
第4题图 第6题图 第7题图 第8题图 第9题图 第10题图
5、根据表格中二次函数y=ax+bx+c的自变量x与函数值y的对应值,可以判断方程ax+bx+c=0的一个解x的范
围是( )
x 0 0.5 1 1.5 2
y=ax+bx+c -1 -0.5 1 3.5 7
A 1.5<x<2 B 1<x<1.5 C 0.5<x<1 D 0<x<0.5
6、如图,点A是反比例函数y=(x>0)图象上任意-点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为( )
A.2 B.1 C.4 D.不能确定
7、以0为中心点的量角器与直角三角板ABC按如图方式摆放,量角器的0刻度线与斜边AB重合,点D为斜边AB上一点,作射线CD交弧AB于点E,如果点E所对应的读数为50°,那么∠BDE的大小为( )
A.100° B.110° C.115° D.130°
8、用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
9、如图,已知AD为ΔABC的角平分线,DE//AB交AC于E,如果AE:EC=3:5,那么AC:AB等于( )
A B C D 2
10、如图,RtΔABC中, AB=AC=3,A0=1,若将AD绕A点逆时针旋转90°得到AE,连接OE,则在D点运动过程中,线段OE的最小值为( )
A.1 B. C. D.2
二、填空题(本大题共4小题,每小题5分,满分20分)
11、已知线段AB=2、P是线段AB的黄金分割点(AP<PB), 那么PB=
12、如图,为了测量山坡的护坡石坝高,把一根长为 4.5m的竹竿AC斜靠在石坝旁,量出竿上AD长为lm时,它离地面的高度DE为0.6m,则坝高CF为_ m.
第12题图 第13题图 第14题图
13、如图所示,AB 是⊙0的直径,弦CD⊥AB于H,∠A=30°,CD=2, 则⊙0的半径是
14、如图,在矩形ABCD中,AB=4,AD=8,点E、F分别在边AD、BC上,且AE=3,按以下步骤操作:第一步,沿直线EF翻折,点A的对应点A'恰好落在对角线AC上,点B的对应点为B',则tan∠AEF=___ _;第二步,分别在EF,A'B'上取点M、N,沿直线MN继续翻折,使点F与点E重合,则线段MN的长为
三、(本大题共2小题,每小题8分,总计16分)
15、计算:tan30°sin60°-cos45°+tan45°
16、在正方形网格中,每个小正方形的边长为1,△ABC在平面直角坐标系中的位置如图所示.
(1)以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为2:1,并写出点A1的坐标;
(2)作出△ABC绕点C逆时针旋转90°后的图形△A2B2C;
四、(本大题共2小题,每小题8分,总计16分)
17、已知二次函数y=x+4x
(1)用配方法把该函数化为y=a(x-h)+k (其中a、h、k都是常数且a≠0)的形式,并指出函数图象的对称轴和顶点坐标;
(2)求函数图象与x轴的交点坐标.
18、如图1,四边形ABCD中, ∠ABD=∠BCD=90°,DB平分∠ADC,若CD=6,AD=8.
(1)求BD的长; (2)如图2,过点B作BW//CD交AD于M,连接CM交DB于N,求DW的长
五、(本大题共2小题,每小题10分,总计20分)
19、随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量翡翠湖某处东西岸边B, C两点之间的距离.如图所示,小星站在湖边的B处遥控无人机,无人机在A处距离地面的飞行高度是161.6m,此时从无人机测得岸边C处的俯角为63°,他抬头仰视无人机时,仰角为a,若小星的身高BE=1.6m, EA=200m(点A、E、B、C在同一平面内)
(1)求仰角a的正弦值;
(2)求B、C两点之间的距离(结果精确到1m)(sin63"≈0.89,cos63°≈0.45,tan63°≈1.96,sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
20、如图,AB是⊙0的切线,D点在⊙0上,AD与⊙0相交于C,CE是⊙0的直径,连接BC,若∠A=90°
(1)求证:CB平分∠ACE; (2)当AB=2,AC=1时,求⊙0的半径长
六、(本大题共1小题,每小题12分,总计12分)
21、如图,直线y1=k1x+b与双曲线在第一象限内交于A、B两点,已知A(1,m)、B(2,1)
(1)求k的值及直线AB的解析式;
(2)根据函数图象,直接写出不等式y1>y2的解集;
(3)设点P是线段AB上的一个动点, 过点P作PD⊥x轴于点D、E是y轴上一点,ΔPED的面积能否达到,
若能达到,请求出此时点P的坐标.
七、(本大题共1小题,每小题12分,总计12分)
22、某公司销售-种商品,成本为每件30元,经过市场调查发现,该商品的日销售量y (件)与销售单价x (元)是一次函数关系,其销售单价、日销售量的三组对应数值如下表:
销售单价x(元) 40 60 80
日销售量y 件) 80 60 40
(1)求公司销售该商品获得的最大日利润;
(2)销售一段时间以后,由于某种原因,该商品每件成本增加了10 元,若物价部门规定该商品销售单价不能超过a元,在日销售量y(件)与销售单价x (元)保持(1)中函数关系不变的情况下,该商品的日销售最大利润是1500元,求a的值.
八、(本大题共1小题,每小题14分,总计14分)
23、△ABC中,∠BAC=90°,AB=AC,D为BC的中点,F、E是AC上两点,连接BE、DF交于△ABC内一点G,且∠EGF=45°
(1)如图1,求证∠FDC=∠AEB;
(2)如图1,若AE=3CE=6,求BG的长:
(3)如图2,若F为AC上任意一点,连接AG,求证:∠EAG=∠ABE;
同课章节目录
