2021-2022学年高一上学期数学北师大版必修二期末复习空间垂直、平行的判定与性质课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版必修二期末复习空间垂直、平行的判定与性质课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
题型剖析
空间垂直、平行的判定与性质
1、空间垂直的判定与性质
例题剖析
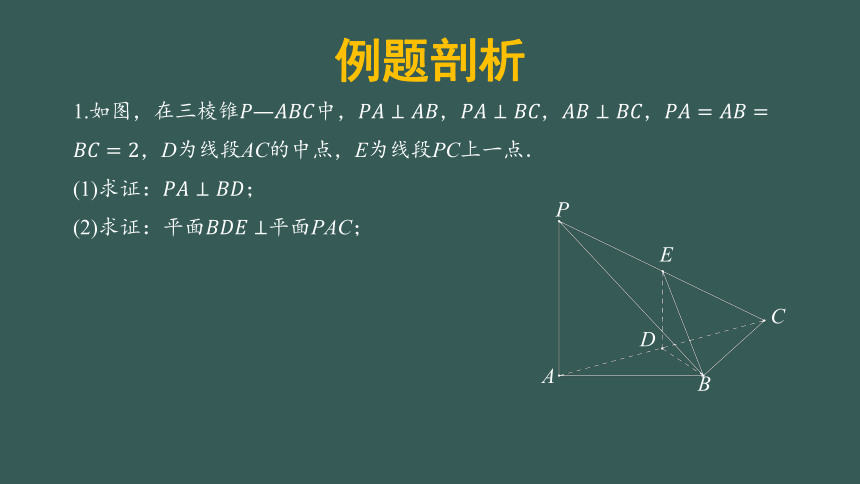
1.如图,在三棱锥中,,,,,D为线段AC的中点,E为线段PC上一点.
(1)求证:;
(2)求证:平面平面PAC;
A
B
C
P
E
D
例题剖析
1.如图,在三棱锥中,,,,,D为线段AC的中点,E为线段PC上一点.
(1)求证:;
A
B
C
P
E
D
证明:
因为,,且,
平面ABC,平面ABC,
所以平面ABC.
又因为平面ABC,所以;
A
B
C
P
E
D
例题剖析
1.如图,在三棱锥中,,,,,D为线段AC的中点,E为线段PC上一点.
(2)求证:平面平面PAC;
证明:
因为,D为AC的中点,所以.
由(1)知,,
且,平面PAC,平面PAC,
所以平面PAC,
又平面BDE,所以平面平面PAC;
例题剖析
2.三棱柱中,侧面为菱形,,,,.求证:面面
面ABC,面面C.
证明:
取BC中点O,连AO,,
O
,,,
,,
又,,
,,
又,
,
,
,面,面,
面,
跟踪训练
如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点.
求证:(1) 平面PAD;(2) .
P
A
B
C
D
G
跟踪训练
如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点.
求证:(1) 平面PAD;
证明:
因为四边形ABCD是菱形,且
所以是正三角形,
因为G是AD的中点,
所以,
又因为平面平面ABCD,平面平面,
面,
所以平面PAD;
P
A
B
C
D
G
跟踪训练
如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点.
求证: (2) .
证明:
P
A
B
C
D
G
因为为正三角形,G为AD的中点,
所以,
又知,而,平面PBG,平面PBG.
所以平面PBG.
又因为平面PBG,
所以.
方法指导
1.面面垂直判定的2种方法与1个转化
(1)2种方法:
①面面垂直的定义;
②面面垂直的判定定理(a⊥β,a α α⊥β).
(2)1个转化:
在已知两个平面垂直时,一般要用性质定理进行转化.在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直.
2.面面垂直性质的应用
(1)两平面垂直的性质定理是把面面垂直转化为线面垂直的依据,运用时要注意“平面内的直线”.
(2)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.
2、空间平行的判定与性质
例题剖析
1.已知四棱锥的底面ABCD是梯形,,,,,点E在棱PC上,且
求证:平面PAD.
平面BEF,平面PAD.
C
P
A
B
D
E
F
证明:
过点B作于点F,连接EF,
,,四边形ABFD为正方形,
,,
,而,,
平面PAD,平面PAD,
平面PAD,同理平面PAD,
,BF,平面BEF,
平面平面PAD,
例题剖析
所以平面平面MNG.
A
B
C
M
D
N
F
E
G
证明:
因为N,G分别为平行四边形ADEF的边AD,EF的中点,
所以,
又平面MNG,平面MNG,所以平面MNG.
又M为AB的中点,
所以MN为的中位线,所以,
又平面MNG,平面MNG,
所以平面MNG,
又,平面BDE,平面BDE,
2.如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.
求证:平面平面MNG.
跟踪训练
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的三等分点靠近B,N靠近;
(1) 求证:平面PAD.
(2) 在PB上确定一点Q,使平面平面PAD.
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的三等分点靠近B,N靠近;
(1) 求证:平面PAD.
证明:
取PD的三等分点靠近D点,如图,连接EN,AE,
是PC的三等分点,E是PD的三等分点,
是AB的三等分点,.
又,,,
四边形AMNE为平行四边形,.
平面PAD,平面PAD,
平面PAD.
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的三等分点靠近B,N靠近;
(2) 在PB上确定一点Q,使平面平面PAD.
证明:
Q
如图,连接MQ,NQ.
若平面平面PAD,
且平面平面,平面平面,
则,
是AB的三等分点,
是PB的三等分点,
即当Q为PB的三等分点时,平面平面PAD.
方法指导
1. 证明线面平行有两种常用方法
①线面平行的判定定理;
②先利用面面平行的判定定理证明面面平行,再根据面面平行的性质证明线面平行.
2. 在应用线面平行的判定定理进行平行转化时,一定注意定理成立的条件,通常应严格按照定理成立的条件规范书写步骤,如:把线面平行转化为线线平行时,必须说清经过已知直线的平面和已知平面相交,这时才有直线与交线平行.
证明面面平行的常用方法
1.利用面面平行的定义或判定定理.
2.利用垂直于同一条直线的两个平面平行(l⊥α,l⊥β α∥β).
3.利用平面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行(α∥β,β∥γ α∥γ).
利用线面平行或面面平行的性质,可以实现与线线平行的转化,尤其在截面图的画法中,常用来确定交线的位置.对于线段长或线段比例问题,常用平行线对应线段成比例或相似三角形来解决.
方法指导
再见
题型剖析
空间垂直、平行的判定与性质
1、空间垂直的判定与性质
例题剖析
1.如图,在三棱锥中,,,,,D为线段AC的中点,E为线段PC上一点.
(1)求证:;
(2)求证:平面平面PAC;
A
B
C
P
E
D
例题剖析
1.如图,在三棱锥中,,,,,D为线段AC的中点,E为线段PC上一点.
(1)求证:;
A
B
C
P
E
D
证明:
因为,,且,
平面ABC,平面ABC,
所以平面ABC.
又因为平面ABC,所以;
A
B
C
P
E
D
例题剖析
1.如图,在三棱锥中,,,,,D为线段AC的中点,E为线段PC上一点.
(2)求证:平面平面PAC;
证明:
因为,D为AC的中点,所以.
由(1)知,,
且,平面PAC,平面PAC,
所以平面PAC,
又平面BDE,所以平面平面PAC;
例题剖析
2.三棱柱中,侧面为菱形,,,,.求证:面面
面ABC,面面C.
证明:
取BC中点O,连AO,,
O
,,,
,,
又,,
,,
又,
,
,
,面,面,
面,
跟踪训练
如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点.
求证:(1) 平面PAD;(2) .
P
A
B
C
D
G
跟踪训练
如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点.
求证:(1) 平面PAD;
证明:
因为四边形ABCD是菱形,且
所以是正三角形,
因为G是AD的中点,
所以,
又因为平面平面ABCD,平面平面,
面,
所以平面PAD;
P
A
B
C
D
G
跟踪训练
如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点.
求证: (2) .
证明:
P
A
B
C
D
G
因为为正三角形,G为AD的中点,
所以,
又知,而,平面PBG,平面PBG.
所以平面PBG.
又因为平面PBG,
所以.
方法指导
1.面面垂直判定的2种方法与1个转化
(1)2种方法:
①面面垂直的定义;
②面面垂直的判定定理(a⊥β,a α α⊥β).
(2)1个转化:
在已知两个平面垂直时,一般要用性质定理进行转化.在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直.
2.面面垂直性质的应用
(1)两平面垂直的性质定理是把面面垂直转化为线面垂直的依据,运用时要注意“平面内的直线”.
(2)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.
2、空间平行的判定与性质
例题剖析
1.已知四棱锥的底面ABCD是梯形,,,,,点E在棱PC上,且
求证:平面PAD.
平面BEF,平面PAD.
C
P
A
B
D
E
F
证明:
过点B作于点F,连接EF,
,,四边形ABFD为正方形,
,,
,而,,
平面PAD,平面PAD,
平面PAD,同理平面PAD,
,BF,平面BEF,
平面平面PAD,
例题剖析
所以平面平面MNG.
A
B
C
M
D
N
F
E
G
证明:
因为N,G分别为平行四边形ADEF的边AD,EF的中点,
所以,
又平面MNG,平面MNG,所以平面MNG.
又M为AB的中点,
所以MN为的中位线,所以,
又平面MNG,平面MNG,
所以平面MNG,
又,平面BDE,平面BDE,
2.如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.
求证:平面平面MNG.
跟踪训练
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的三等分点靠近B,N靠近;
(1) 求证:平面PAD.
(2) 在PB上确定一点Q,使平面平面PAD.
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的三等分点靠近B,N靠近;
(1) 求证:平面PAD.
证明:
取PD的三等分点靠近D点,如图,连接EN,AE,
是PC的三等分点,E是PD的三等分点,
是AB的三等分点,.
又,,,
四边形AMNE为平行四边形,.
平面PAD,平面PAD,
平面PAD.
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的三等分点靠近B,N靠近;
(2) 在PB上确定一点Q,使平面平面PAD.
证明:
Q
如图,连接MQ,NQ.
若平面平面PAD,
且平面平面,平面平面,
则,
是AB的三等分点,
是PB的三等分点,
即当Q为PB的三等分点时,平面平面PAD.
方法指导
1. 证明线面平行有两种常用方法
①线面平行的判定定理;
②先利用面面平行的判定定理证明面面平行,再根据面面平行的性质证明线面平行.
2. 在应用线面平行的判定定理进行平行转化时,一定注意定理成立的条件,通常应严格按照定理成立的条件规范书写步骤,如:把线面平行转化为线线平行时,必须说清经过已知直线的平面和已知平面相交,这时才有直线与交线平行.
证明面面平行的常用方法
1.利用面面平行的定义或判定定理.
2.利用垂直于同一条直线的两个平面平行(l⊥α,l⊥β α∥β).
3.利用平面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行(α∥β,β∥γ α∥γ).
利用线面平行或面面平行的性质,可以实现与线线平行的转化,尤其在截面图的画法中,常用来确定交线的位置.对于线段长或线段比例问题,常用平行线对应线段成比例或相似三角形来解决.
方法指导
再见
