2021--2022学年人教版八年级数学下册第16章 二次根式 单元检测题(word版、含答案)
文档属性
| 名称 | 2021--2022学年人教版八年级数学下册第16章 二次根式 单元检测题(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 21:18:19 | ||
图片预览


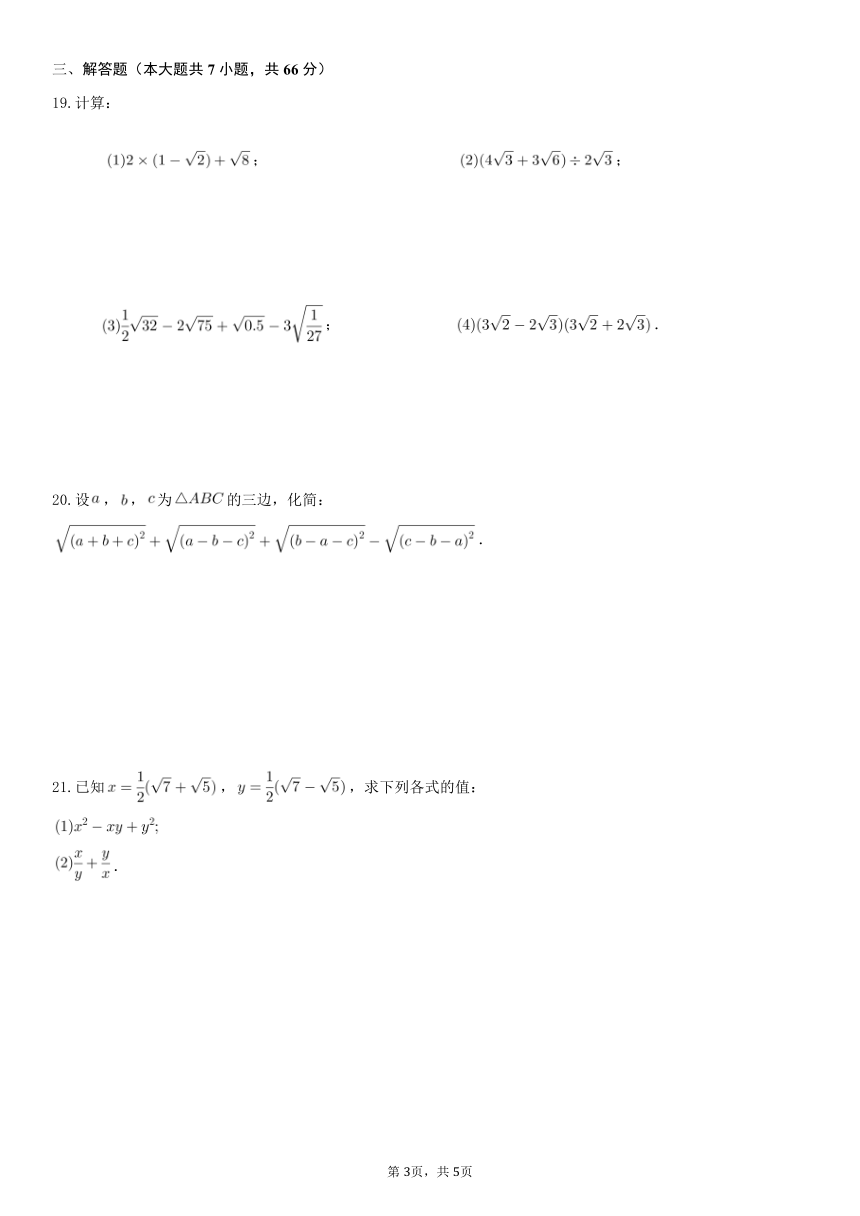

文档简介
八年级数学下册第16章《二次根式》单元质量检测题
分值:120分 时间:90分钟
一、选择题(本大题共12道小题,共36分)
若有意义,则的取值范围是
A. B. C. D.
下列根式中是最简二次根式的是
A. B. C. D.
实数,在数轴上对应点的位置如图所示,且,则化简的结果为
A. B. C. D.
下列计算正确的是
A. B.
C. D.
,则
A. B. C. D.
已知,则的平方根是
A. B. C. D.
把代数式中的移到根号内,那么这个代数式等于
A. B. C. D.
已知,则的值为
A. B. C. D.
若、是实数,且,则的值是
A. 或 B. 或 C. 或 D. 或
已知,则的值为
A. B. C. D.
设,,,则,,的大小关系是
A. B. C. D.
对于,某校数学兴趣小组研究了四个问题,其中正确的有
的值随的变化而变化,当时,此代数式有最小值
在的条件下化简代数式的结果为
当的值恒为定值时,字母的取值范围是
若,则字母必须满足
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共6小题,共18分)
已知:,则______.
已知,是实数,且满足,则的值是______.
若,则 .
已知,则_____.
已知实数、、在数轴上的位置如图所示,化简 .
观察下列等式:
,
,
,
请你根据以上规律,写出第个等式______.
三、解答题(本大题共7小题,共66分)
19.计算:
; ;
; .
20.设,,为的三边,化简:
.
21.已知,,求下列各式的值:
.
22.已知,,满足.
求,,的值.
试问以,,为边能否构成三角形?若能构成三角形,请求出三角形的周长;若不能,请说明理由.
23.如图,有一张边长为的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为求:
剪掉四个角后,制作长方体盒子的纸板的面积;
长方体盒子的体积.
24.观察下列各式:
;
;
.
根据你发现的规律填空:
______________________.
猜想为自然数的值,并通过计算证实你的猜想.
25.阅读材料,并回答问题:
形如,的数可以化简,其化简的目的主要把原数分母中的无理数化为有理数,如,,这样的化简过程叫做分母有理化.
我们把叫做的有理化因式,叫做的有理化因式.
问题:的有理化因式是______,的有理化因式是______.
应用:分母有理化.
拓展:比较大小与.
第2页,共3页
第1页,共1页
答案和解析
选择题(本大题共12道小题,共36分)
二、填空题(本大题共6小题,共18分)
13、
14、
15、
16、
17、
18、
三、解答题(本大题共7小题,共66分)
19、解:原式;
原式;
原式;;
原式.
20、解:根据,,为的三边,
得到,,,,
则原式
.
21、解:,,
, .
.
.
22、解:,,满足,
,,,
,,;
,,
以,,为边能构成三角形.
三角形的周长为.
23、解:长方体盒子的纸板的面积:,
答:剪掉四个角后,制作长方体盒子的纸板的面积为.
长方体盒子的体积:.
答:长方体盒子的体积为.
24、解:;;
猜想:.
验证:当,为自然数时,,
所以左边右边,原式成立.
25、解:;
;
,
,
而
,
,,
.
分值:120分 时间:90分钟
一、选择题(本大题共12道小题,共36分)
若有意义,则的取值范围是
A. B. C. D.
下列根式中是最简二次根式的是
A. B. C. D.
实数,在数轴上对应点的位置如图所示,且,则化简的结果为
A. B. C. D.
下列计算正确的是
A. B.
C. D.
,则
A. B. C. D.
已知,则的平方根是
A. B. C. D.
把代数式中的移到根号内,那么这个代数式等于
A. B. C. D.
已知,则的值为
A. B. C. D.
若、是实数,且,则的值是
A. 或 B. 或 C. 或 D. 或
已知,则的值为
A. B. C. D.
设,,,则,,的大小关系是
A. B. C. D.
对于,某校数学兴趣小组研究了四个问题,其中正确的有
的值随的变化而变化,当时,此代数式有最小值
在的条件下化简代数式的结果为
当的值恒为定值时,字母的取值范围是
若,则字母必须满足
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共6小题,共18分)
已知:,则______.
已知,是实数,且满足,则的值是______.
若,则 .
已知,则_____.
已知实数、、在数轴上的位置如图所示,化简 .
观察下列等式:
,
,
,
请你根据以上规律,写出第个等式______.
三、解答题(本大题共7小题,共66分)
19.计算:
; ;
; .
20.设,,为的三边,化简:
.
21.已知,,求下列各式的值:
.
22.已知,,满足.
求,,的值.
试问以,,为边能否构成三角形?若能构成三角形,请求出三角形的周长;若不能,请说明理由.
23.如图,有一张边长为的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为求:
剪掉四个角后,制作长方体盒子的纸板的面积;
长方体盒子的体积.
24.观察下列各式:
;
;
.
根据你发现的规律填空:
______________________.
猜想为自然数的值,并通过计算证实你的猜想.
25.阅读材料,并回答问题:
形如,的数可以化简,其化简的目的主要把原数分母中的无理数化为有理数,如,,这样的化简过程叫做分母有理化.
我们把叫做的有理化因式,叫做的有理化因式.
问题:的有理化因式是______,的有理化因式是______.
应用:分母有理化.
拓展:比较大小与.
第2页,共3页
第1页,共1页
答案和解析
选择题(本大题共12道小题,共36分)
二、填空题(本大题共6小题,共18分)
13、
14、
15、
16、
17、
18、
三、解答题(本大题共7小题,共66分)
19、解:原式;
原式;
原式;;
原式.
20、解:根据,,为的三边,
得到,,,,
则原式
.
21、解:,,
, .
.
.
22、解:,,满足,
,,,
,,;
,,
以,,为边能构成三角形.
三角形的周长为.
23、解:长方体盒子的纸板的面积:,
答:剪掉四个角后,制作长方体盒子的纸板的面积为.
长方体盒子的体积:.
答:长方体盒子的体积为.
24、解:;;
猜想:.
验证:当,为自然数时,,
所以左边右边,原式成立.
25、解:;
;
,
,
而
,
,,
.
