2021--2022学年人教版九年级下册数学26.1.2 反比例函数的图像及性质 复习培优专题(word版、含答案)
文档属性
| 名称 | 2021--2022学年人教版九年级下册数学26.1.2 反比例函数的图像及性质 复习培优专题(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 384.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 21:24:35 | ||
图片预览



文档简介
人教版九年级下册数学人教版九年级下册数学
《反比例函数的图像及性质》靶向复习培优专题
一、选择题。
1.已知反比例函数的图象位于第二、四象限,则的取值范围为( )
A. B. C. D.
2. 对于反比例函数,下列说法不正确的是( )
A. 它的图象是双曲线并且在第一、三象限
B. 点(-4,)在它的图象上
C. 它的图象是中心对称图形
D. 随的增大而增大
3. 根据下表中,反比例函数的自变量x与函数y的对应值,可得p的值为( )
A. 3 B. 1 C. -2 D. -6
4. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
5. 已知和均是以为自变量的函数,当时,函数值分别为和,若存在实数,使得,则称函数和具有性质.以下函数和具有性质的是( )
A.和 B.和
C.和 D.和
6. 一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
7. 如图,反比例函数(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A. B. C. D.
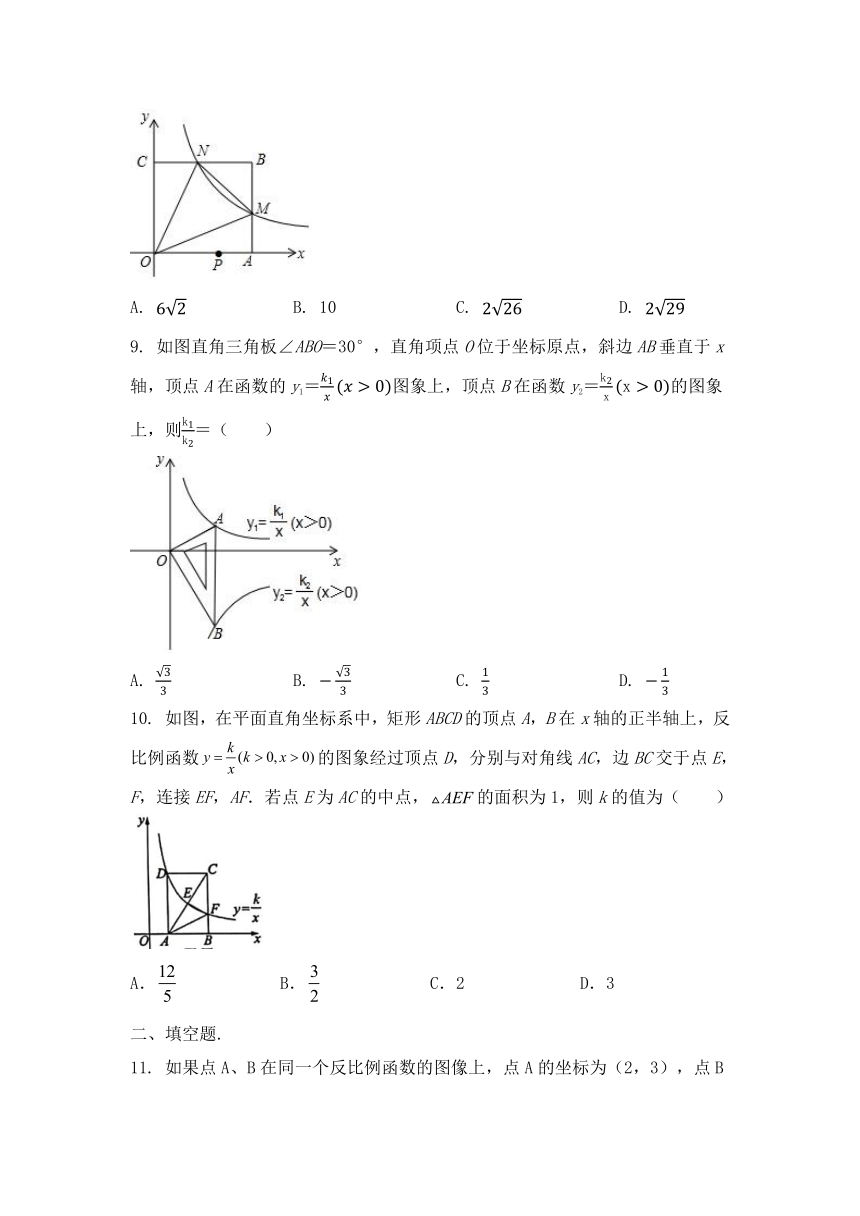
8. 如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. B. 10 C. D.
9. 如图直角三角板∠ABO=30°,直角项点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的y1=图象上,顶点B在函数y2=的图象上,则=( )
A. B. C. D.
10. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
二、填空题.
11. 如果点A、B在同一个反比例函数的图像上,点A的坐标为(2,3),点B横坐标为3,那么点B的纵坐标是___.
12. 若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
13. 如果一个正比例函数的图象与一个反比例函数的图象交,那么值为_______.
14.如图,在平面直角坐标系中直线与轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线向上平移后与反比例函数图象在第一象限内交于点C,且的面积为18,求平移后的直线的函数关系式是______.
15. 如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线经过点C交x轴于点E,双曲线经过点D,则k的值为___.
16.反比例函数y1=,y2=(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k=________ .
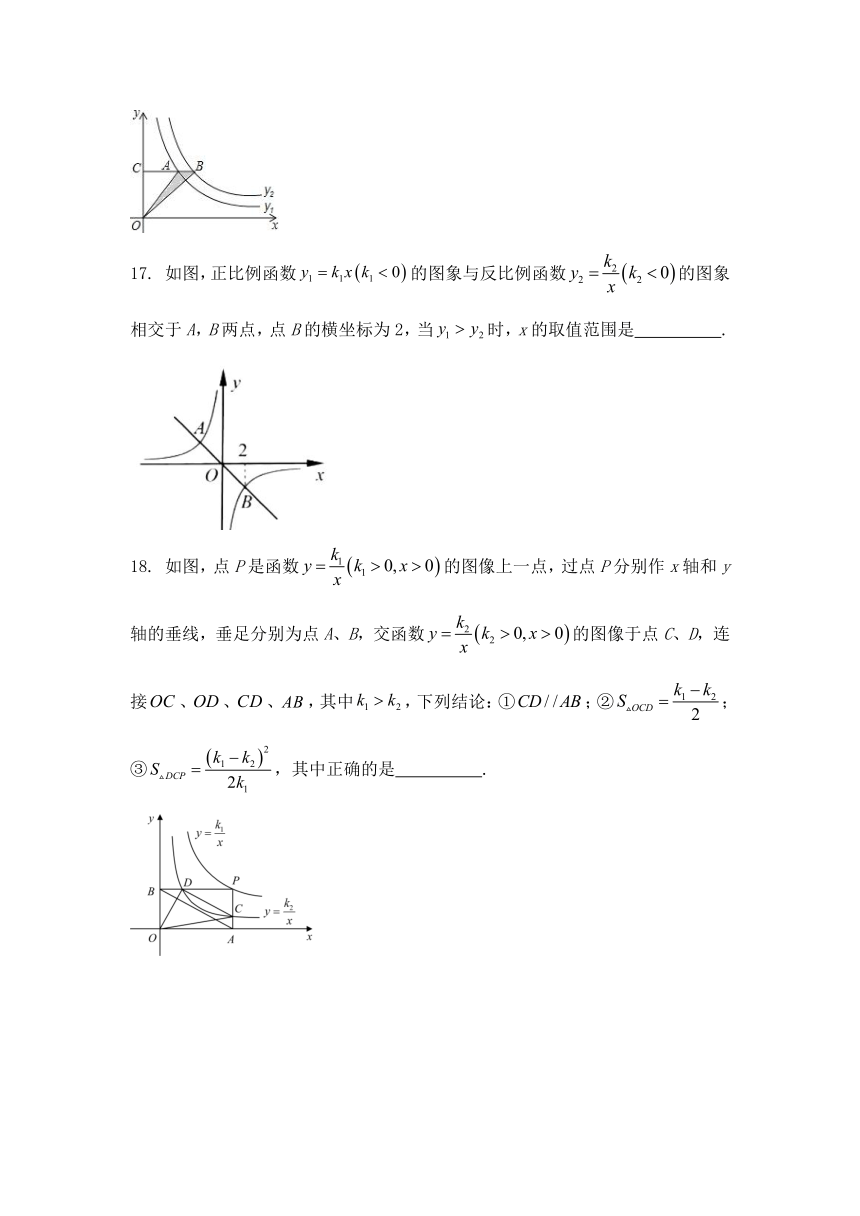
17. 如图,正比例函数的图象与反比例函数的图象相交于A,B两点,点B的横坐标为2,当时,x的取值范围是 .
18. 如图,点P是函数的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数的图像于点C、D,连接、、、,其中,下列结论:①;②;③,其中正确的是 .
三、解答题.
19.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数(m≠0)的图象交于点A(3,1),且过点B(0,-2).
(1)求反比例函数和一次函数的表达式.
(2)如果点P是x轴上位于直线AB右侧的一点,且ΔABP的面积是3,求点P的坐标.
20.如图,反比例函数y=(k≠0,x<0)的图象过等边△AOB的顶点A.已如点B在x轴上,且B(﹣4,0).
(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图象上,需将△AOB向上平移多少个单位长度?
21. 如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求一次函数和反比例函数的解析式;
(2)点在轴上,且满足的面积等于4,请直接写出点的坐标.
22. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标随时间(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分.
(1)求点对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
人教版九年级下册数学人教版九年级下册数学
《反比例函数的图像及性质》靶向复习培优专题
一、选择题。
1.已知反比例函数的图象位于第二、四象限,则的取值范围为( )
A. B. C. D.
选C.
2. 对于反比例函数,下列说法不正确的是( )
A. 它的图象是双曲线并且在第一、三象限
B. 点(-4,)在它的图象上
C. 它的图象是中心对称图形
D. 随的增大而增大
选D.
3. 根据下表中,反比例函数的自变量x与函数y的对应值,可得p的值为( )
A. 3 B. 1 C. -2 D. -6
选D.
4. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
选C
5. 已知和均是以为自变量的函数,当时,函数值分别为和,若存在实数,使得,则称函数和具有性质.以下函数和具有性质的是( )
A.和 B.和
C.和 D.和
选A
6. 一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
选B
7. 如图,反比例函数(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A. B. C. D.
选D.
8. 如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. B. 10 C. D.
选:C.
9. 如图直角三角板∠ABO=30°,直角项点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的y1=图象上,顶点B在函数y2=的图象上,则=( )
A. B. C. D.
选:D
10. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
选:D
二、填空题.
11. 如果点A、B在同一个反比例函数的图像上,点A的坐标为(2,3),点B横坐标为3,那么点B的纵坐标是___.
答案:.
12. 若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
答案:
13. 如果一个正比例函数的图象与一个反比例函数的图象交,那么值为_______.
答案:.
14.如图,在平面直角坐标系中直线与轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线向上平移后与反比例函数图象在第一象限内交于点C,且的面积为18,求平移后的直线的函数关系式是______.
答案:y=x+7.
15. 如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线经过点C交x轴于点E,双曲线经过点D,则k的值为___.
答案:1.
16.反比例函数y1=,y2=(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k=________ .
答案:12.
17. 如图,正比例函数的图象与反比例函数的图象相交于A,B两点,点B的横坐标为2,当时,x的取值范围是 .
答案:或
18. 如图,点P是函数的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数的图像于点C、D,连接、、、,其中,下列结论:①;②;③,其中正确的是 .
答案:①③.
三、解答题.
19.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数(m≠0)的图象交于点A(3,1),且过点B(0,-2).
(1)求反比例函数和一次函数的表达式.
(2)如果点P是x轴上位于直线AB右侧的一点,且ΔABP的面积是3,求点P的坐标.
【解析】
(1)∵反比例函数(m≠0)的图象过点A(3,1),
∴,
∴ m=3,
∴反比例函数的表达式为.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,-2),
∴解得
∴一次函数的表达式y=x-2.
(2)如图,设一次函数y=x-2的图象与x轴的交点为C,
令y=0,则x-2=0,x=2,
∴点C的坐标为(2,0).
∵
∴
∴PC=2
∵点P是x轴上位于直线AB右侧的一点,
∴点P的坐标为(4,0).
20.如图,反比例函数y=(k≠0,x<0)的图象过等边△AOB的顶点A.已如点B在x轴上,且B(﹣4,0).
(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图象上,需将△AOB向上平移多少个单位长度?
【解析】
(1)过点A作AC⊥x轴于点C,
∵△AOB是等边三角形,B(-2,0),
∴OC=1,AC=,
∴点A的坐标为:(-1,),
∴,
解得:k=-,
∴反比例函数的表达式为:;
(2)∵当x=-2时,y=,
∴要使点B在上述反比例函数的图象上,需将△ABC向上平移个单位长度.
21. 如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求一次函数和反比例函数的解析式;
(2)点在轴上,且满足的面积等于4,请直接写出点的坐标.
【解析】
(1)由题意可得:
点B(3,-2)在反比例函数图像上,
∴,则m=-6,
∴反比例函数的解析式为,
将A(-1,n)代入,
得:,即A(-1,6),
将A,B代入一次函数解析式中,得
,解得:,
∴一次函数解析式为;
(2)∵点P在x轴上,
设点P的坐标为(a,0),
∵一次函数解析式为,令y=0,则x=2,
∴直线AB与x轴交于点(2,0),
由△ABP的面积为4,可得:
,即,
解得:a=1或a=3,
∴点P的坐标为(1,0)或(3,0).
22. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标随时间(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分.
(1)求点对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
【解析】
(1)令反比例函数为,由图可知点在的图象上,
∴,
∴.将x=45代入
将x=45代入得:
点对应的指标值为.
(2)设直线的解析式为,将、代入中,
得,解得.
∴直线的解析式为.
由题得,解得.
∵,
∴张老师经过适当的安排,能使学生在听综合题的讲解时,注意力指标都不低于36.
《反比例函数的图像及性质》靶向复习培优专题
一、选择题。
1.已知反比例函数的图象位于第二、四象限,则的取值范围为( )
A. B. C. D.
2. 对于反比例函数,下列说法不正确的是( )
A. 它的图象是双曲线并且在第一、三象限
B. 点(-4,)在它的图象上
C. 它的图象是中心对称图形
D. 随的增大而增大
3. 根据下表中,反比例函数的自变量x与函数y的对应值,可得p的值为( )
A. 3 B. 1 C. -2 D. -6
4. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
5. 已知和均是以为自变量的函数,当时,函数值分别为和,若存在实数,使得,则称函数和具有性质.以下函数和具有性质的是( )
A.和 B.和
C.和 D.和
6. 一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
7. 如图,反比例函数(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A. B. C. D.
8. 如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. B. 10 C. D.
9. 如图直角三角板∠ABO=30°,直角项点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的y1=图象上,顶点B在函数y2=的图象上,则=( )
A. B. C. D.
10. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
二、填空题.
11. 如果点A、B在同一个反比例函数的图像上,点A的坐标为(2,3),点B横坐标为3,那么点B的纵坐标是___.
12. 若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
13. 如果一个正比例函数的图象与一个反比例函数的图象交,那么值为_______.
14.如图,在平面直角坐标系中直线与轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线向上平移后与反比例函数图象在第一象限内交于点C,且的面积为18,求平移后的直线的函数关系式是______.
15. 如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线经过点C交x轴于点E,双曲线经过点D,则k的值为___.
16.反比例函数y1=,y2=(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k=________ .
17. 如图,正比例函数的图象与反比例函数的图象相交于A,B两点,点B的横坐标为2,当时,x的取值范围是 .
18. 如图,点P是函数的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数的图像于点C、D,连接、、、,其中,下列结论:①;②;③,其中正确的是 .
三、解答题.
19.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数(m≠0)的图象交于点A(3,1),且过点B(0,-2).
(1)求反比例函数和一次函数的表达式.
(2)如果点P是x轴上位于直线AB右侧的一点,且ΔABP的面积是3,求点P的坐标.
20.如图,反比例函数y=(k≠0,x<0)的图象过等边△AOB的顶点A.已如点B在x轴上,且B(﹣4,0).
(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图象上,需将△AOB向上平移多少个单位长度?
21. 如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求一次函数和反比例函数的解析式;
(2)点在轴上,且满足的面积等于4,请直接写出点的坐标.
22. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标随时间(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分.
(1)求点对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
人教版九年级下册数学人教版九年级下册数学
《反比例函数的图像及性质》靶向复习培优专题
一、选择题。
1.已知反比例函数的图象位于第二、四象限,则的取值范围为( )
A. B. C. D.
选C.
2. 对于反比例函数,下列说法不正确的是( )
A. 它的图象是双曲线并且在第一、三象限
B. 点(-4,)在它的图象上
C. 它的图象是中心对称图形
D. 随的增大而增大
选D.
3. 根据下表中,反比例函数的自变量x与函数y的对应值,可得p的值为( )
A. 3 B. 1 C. -2 D. -6
选D.
4. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
选C
5. 已知和均是以为自变量的函数,当时,函数值分别为和,若存在实数,使得,则称函数和具有性质.以下函数和具有性质的是( )
A.和 B.和
C.和 D.和
选A
6. 一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
选B
7. 如图,反比例函数(k<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A. B. C. D.
选D.
8. 如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A. B. 10 C. D.
选:C.
9. 如图直角三角板∠ABO=30°,直角项点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数的y1=图象上,顶点B在函数y2=的图象上,则=( )
A. B. C. D.
选:D
10. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
选:D
二、填空题.
11. 如果点A、B在同一个反比例函数的图像上,点A的坐标为(2,3),点B横坐标为3,那么点B的纵坐标是___.
答案:.
12. 若点在反比例函数的图象上,则____(填“>”或“<”或“=”)
答案:
13. 如果一个正比例函数的图象与一个反比例函数的图象交,那么值为_______.
答案:.
14.如图,在平面直角坐标系中直线与轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线向上平移后与反比例函数图象在第一象限内交于点C,且的面积为18,求平移后的直线的函数关系式是______.
答案:y=x+7.
15. 如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线经过点C交x轴于点E,双曲线经过点D,则k的值为___.
答案:1.
16.反比例函数y1=,y2=(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k=________ .
答案:12.
17. 如图,正比例函数的图象与反比例函数的图象相交于A,B两点,点B的横坐标为2,当时,x的取值范围是 .
答案:或
18. 如图,点P是函数的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数的图像于点C、D,连接、、、,其中,下列结论:①;②;③,其中正确的是 .
答案:①③.
三、解答题.
19.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数(m≠0)的图象交于点A(3,1),且过点B(0,-2).
(1)求反比例函数和一次函数的表达式.
(2)如果点P是x轴上位于直线AB右侧的一点,且ΔABP的面积是3,求点P的坐标.
【解析】
(1)∵反比例函数(m≠0)的图象过点A(3,1),
∴,
∴ m=3,
∴反比例函数的表达式为.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,-2),
∴解得
∴一次函数的表达式y=x-2.
(2)如图,设一次函数y=x-2的图象与x轴的交点为C,
令y=0,则x-2=0,x=2,
∴点C的坐标为(2,0).
∵
∴
∴PC=2
∵点P是x轴上位于直线AB右侧的一点,
∴点P的坐标为(4,0).
20.如图,反比例函数y=(k≠0,x<0)的图象过等边△AOB的顶点A.已如点B在x轴上,且B(﹣4,0).
(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图象上,需将△AOB向上平移多少个单位长度?
【解析】
(1)过点A作AC⊥x轴于点C,
∵△AOB是等边三角形,B(-2,0),
∴OC=1,AC=,
∴点A的坐标为:(-1,),
∴,
解得:k=-,
∴反比例函数的表达式为:;
(2)∵当x=-2时,y=,
∴要使点B在上述反比例函数的图象上,需将△ABC向上平移个单位长度.
21. 如图,一次函数的图象与反比例函数的图象交于,两点.
(1)求一次函数和反比例函数的解析式;
(2)点在轴上,且满足的面积等于4,请直接写出点的坐标.
【解析】
(1)由题意可得:
点B(3,-2)在反比例函数图像上,
∴,则m=-6,
∴反比例函数的解析式为,
将A(-1,n)代入,
得:,即A(-1,6),
将A,B代入一次函数解析式中,得
,解得:,
∴一次函数解析式为;
(2)∵点P在x轴上,
设点P的坐标为(a,0),
∵一次函数解析式为,令y=0,则x=2,
∴直线AB与x轴交于点(2,0),
由△ABP的面积为4,可得:
,即,
解得:a=1或a=3,
∴点P的坐标为(1,0)或(3,0).
22. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标随时间(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分.
(1)求点对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于36?请说明理由.
【解析】
(1)令反比例函数为,由图可知点在的图象上,
∴,
∴.将x=45代入
将x=45代入得:
点对应的指标值为.
(2)设直线的解析式为,将、代入中,
得,解得.
∴直线的解析式为.
由题得,解得.
∵,
∴张老师经过适当的安排,能使学生在听综合题的讲解时,注意力指标都不低于36.
