2021—2022学年沪科版九年级数学下册24.1旋转 同步练习(word版含答案)
文档属性
| 名称 | 2021—2022学年沪科版九年级数学下册24.1旋转 同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 156.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-27 00:00:00 | ||
图片预览

文档简介
24.1旋转课时作业
一、选择题
1.下列运动中,不属于旋转的是 ( )
A.钟摆的运动
B.风力发电机风叶的转动
C.汽车方向盘的转动
D.观光电梯的升降运动
2.下列四张扑克牌图案中,属于中心对称的是( )
3.我们知道,国旗上的五角星是旋转对称图形,它旋转与自身重合时,至少需要旋转( )
A.36° B.60° C.45° D.72°
4.将正六边形绕其对称中心旋转后,恰好能与原来的正六边形重合,那么旋转的角度至少是 ( )
A.120° B.60° C.45° D.30°
5.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长是 ( )
A.1 cm B.2 cm C. cm D.2 cm
6. 如图,将Rt△ABC绕着直角顶点C旋转得到Rt△DEC,使点A的对应点D恰好是AB边的中点,则下列结论中错误的是 ( )
A.AC=CD B.∠ACD=∠BCE
C.CD∶AB=1∶2 D.AC∶CE=1∶
7 如图在△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在AB边上,则∠CAA'的度数是 ( )
A.50° B.70°
C.110° D.120°
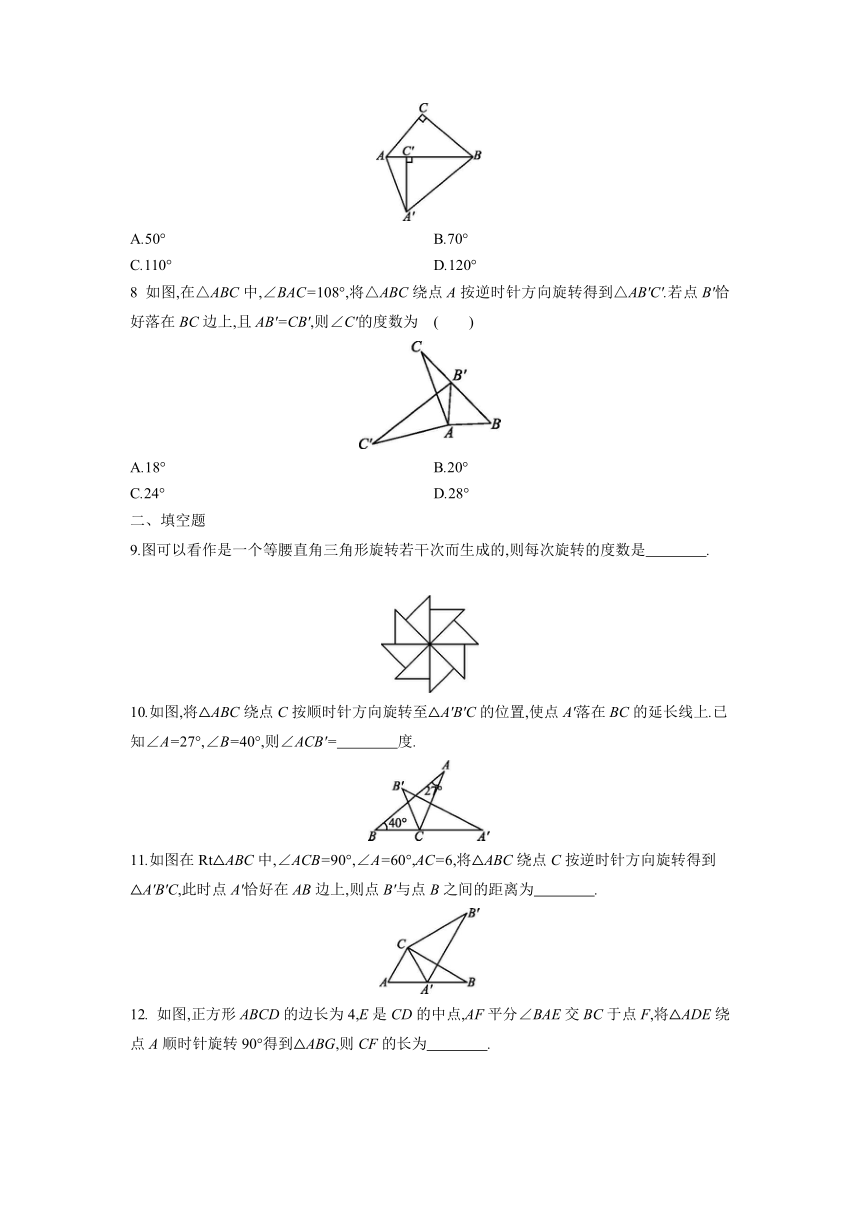
8 如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为 ( )
A.18° B.20°
C.24° D.28°
填空题
9.图可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数是 .
10.如图,将△ABC绕点C按顺时针方向旋转至△A'B'C的位置,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'= 度.
11.如图在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C,此时点A'恰好在AB边上,则点B'与点B之间的距离为 .
12. 如图,正方形ABCD的边长为4,E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得到△ABG,则CF的长为 .
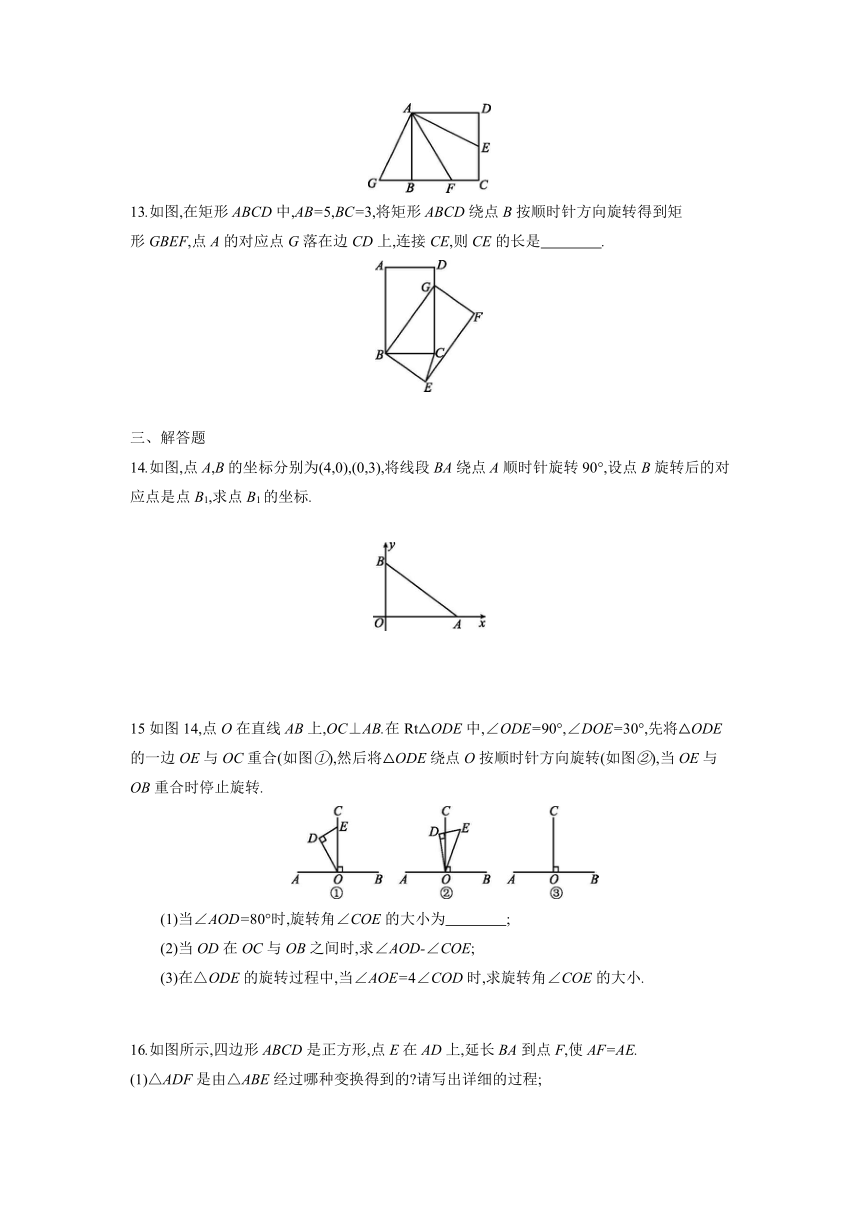
13.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩
形GBEF,点A的对应点G落在边CD上,连接CE,则CE的长是 .
解答题
14.如图,点A,B的坐标分别为(4,0),(0,3),将线段BA绕点A顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.
15如图14,点O在直线AB上,OC⊥AB.在Rt△ODE中,∠ODE=90°,∠DOE=30°,先将△ODE的一边OE与OC重合(如图①),然后将△ODE绕点O按顺时针方向旋转(如图②),当OE与OB重合时停止旋转.
(1)当∠AOD=80°时,旋转角∠COE的大小为 ;
(2)当OD在OC与OB之间时,求∠AOD-∠COE;
(3)在△ODE的旋转过程中,当∠AOE=4∠COD时,求旋转角∠COE的大小.
16.如图所示,四边形ABCD是正方形,点E在AD上,延长BA到点F,使AF=AE.
(1)△ADF是由△ABE经过哪种变换得到的 请写出详细的过程;
(2)如果∠F=70°,求∠EBA的度数;
(3)试说明DF与BE的数量与位置关系.
答案
1.答案为:D.
2.答案为:B
3.答案为:D.
4.答案为:B
5.答案为:C.
6.答案为:C;
7.答案为:B
8.答案为:D;
9.[答案] 45°
10.[答案] 46
11.[答案] 6
12.[答案] 6-2
[解析] 作FM⊥AD于点M,FN⊥AG于点N,如图所示,易得四边形CFMD为矩形,则FM=4.
∵正方形ABCD的边长为4,E是CD的中点,
∴DE=2,∴AE==2.
∵△ADE绕点A顺时针旋转90°得到△ABG,
∴AG=AE=2,BG=DE=2,∠3=∠4,∠GAE=90°,∠ABG=∠D=90°.
而∠ABC=90°,∴点G在CB的延长线上.
∵AF平分∠BAE交BC于点F,∴∠1=∠2,
∴∠2+∠4=∠1+∠3,即AF平分∠GAD,
∴FN=FM=4.
∵AB·GF=FN·AG,
∴GF==2,
∴CF=CG-GF=4+2-2=6-2.
故答案为6-2.
13.
14.解:如图,作B1C⊥x轴于点C.
∵A(4,0),B(0,3),∴OA=4,OB=3.
∵线段BA绕点A顺时针旋转90°得线段AB1,
∴BA=AB1,且∠BAB1=90°,
∴∠BAO+∠B1AC=90°.
而∠BAO+∠ABO=90°,
∴∠ABO=∠B1AC.
又∵∠AOB=∠B1CA=90°,
∴△ABO≌△B1AC,
∴AC=OB=3,B1C=OA=4,
∴OC=OA+AC=7,∴点B1的坐标为(7,4).
15解:(1)∵∠AOE=∠AOD+∠DOE=80°+30°=110°,
∴∠COE=∠AOE-∠AOC=110°-90°=20°.故答案为:20°.
(2)∠AOD-∠COE=(∠AOC+∠COD)-(∠COD+∠DOE)=∠AOC+∠COD-∠COD-∠DOE=∠AOC-∠DOE=90°-30°=60°.
(3)设∠COE=x.
当OD在OA与OC之间时,∠AOE=∠AOC+∠COE=90°+x,∠COD=∠DOE-∠COE=30°-x.
由题意,得90°+x=4(30°-x),
解得x=6°.
当OD在OC与OB之间时,∠AOE=∠AOC+∠COE=90°+x,∠COD=∠COE-∠DOE=x-30°.
由题意,得90°+x=4(x-30°),
解得x=70°.
综上所述,当∠AOE=4∠COD时,旋转角∠COE的大小为6°或70°.
16.解:(1)△ADF是由△ABE绕点A逆时针旋转90°得到的.
(2)∵△ADF是由△ABE旋转得到的,
∴由图形旋转的性质知∠EBA=∠FDA=90°-70°=20°.
(3)如图,延长BE交DF于点G,则∠AEB=∠DEG.
由(1)可知∠EBA=∠ADF,
∴∠EGD=180°-∠ADF-∠DEG=180°-∠EBA-∠AEB=∠DAB=90°,
∴DF与BE垂直.
又由旋转的性质知DF=BE,
∴DF与BE垂直且相等.
一、选择题
1.下列运动中,不属于旋转的是 ( )
A.钟摆的运动
B.风力发电机风叶的转动
C.汽车方向盘的转动
D.观光电梯的升降运动
2.下列四张扑克牌图案中,属于中心对称的是( )
3.我们知道,国旗上的五角星是旋转对称图形,它旋转与自身重合时,至少需要旋转( )
A.36° B.60° C.45° D.72°
4.将正六边形绕其对称中心旋转后,恰好能与原来的正六边形重合,那么旋转的角度至少是 ( )
A.120° B.60° C.45° D.30°
5.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',使点C'落在AB边上,连接BB',则BB'的长是 ( )
A.1 cm B.2 cm C. cm D.2 cm
6. 如图,将Rt△ABC绕着直角顶点C旋转得到Rt△DEC,使点A的对应点D恰好是AB边的中点,则下列结论中错误的是 ( )
A.AC=CD B.∠ACD=∠BCE
C.CD∶AB=1∶2 D.AC∶CE=1∶
7 如图在△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A'BC',使点C的对应点C'恰好落在AB边上,则∠CAA'的度数是 ( )
A.50° B.70°
C.110° D.120°
8 如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为 ( )
A.18° B.20°
C.24° D.28°
填空题
9.图可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数是 .
10.如图,将△ABC绕点C按顺时针方向旋转至△A'B'C的位置,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'= 度.
11.如图在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C,此时点A'恰好在AB边上,则点B'与点B之间的距离为 .
12. 如图,正方形ABCD的边长为4,E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得到△ABG,则CF的长为 .
13.如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩
形GBEF,点A的对应点G落在边CD上,连接CE,则CE的长是 .
解答题
14.如图,点A,B的坐标分别为(4,0),(0,3),将线段BA绕点A顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.
15如图14,点O在直线AB上,OC⊥AB.在Rt△ODE中,∠ODE=90°,∠DOE=30°,先将△ODE的一边OE与OC重合(如图①),然后将△ODE绕点O按顺时针方向旋转(如图②),当OE与OB重合时停止旋转.
(1)当∠AOD=80°时,旋转角∠COE的大小为 ;
(2)当OD在OC与OB之间时,求∠AOD-∠COE;
(3)在△ODE的旋转过程中,当∠AOE=4∠COD时,求旋转角∠COE的大小.
16.如图所示,四边形ABCD是正方形,点E在AD上,延长BA到点F,使AF=AE.
(1)△ADF是由△ABE经过哪种变换得到的 请写出详细的过程;
(2)如果∠F=70°,求∠EBA的度数;
(3)试说明DF与BE的数量与位置关系.
答案
1.答案为:D.
2.答案为:B
3.答案为:D.
4.答案为:B
5.答案为:C.
6.答案为:C;
7.答案为:B
8.答案为:D;
9.[答案] 45°
10.[答案] 46
11.[答案] 6
12.[答案] 6-2
[解析] 作FM⊥AD于点M,FN⊥AG于点N,如图所示,易得四边形CFMD为矩形,则FM=4.
∵正方形ABCD的边长为4,E是CD的中点,
∴DE=2,∴AE==2.
∵△ADE绕点A顺时针旋转90°得到△ABG,
∴AG=AE=2,BG=DE=2,∠3=∠4,∠GAE=90°,∠ABG=∠D=90°.
而∠ABC=90°,∴点G在CB的延长线上.
∵AF平分∠BAE交BC于点F,∴∠1=∠2,
∴∠2+∠4=∠1+∠3,即AF平分∠GAD,
∴FN=FM=4.
∵AB·GF=FN·AG,
∴GF==2,
∴CF=CG-GF=4+2-2=6-2.
故答案为6-2.
13.
14.解:如图,作B1C⊥x轴于点C.
∵A(4,0),B(0,3),∴OA=4,OB=3.
∵线段BA绕点A顺时针旋转90°得线段AB1,
∴BA=AB1,且∠BAB1=90°,
∴∠BAO+∠B1AC=90°.
而∠BAO+∠ABO=90°,
∴∠ABO=∠B1AC.
又∵∠AOB=∠B1CA=90°,
∴△ABO≌△B1AC,
∴AC=OB=3,B1C=OA=4,
∴OC=OA+AC=7,∴点B1的坐标为(7,4).
15解:(1)∵∠AOE=∠AOD+∠DOE=80°+30°=110°,
∴∠COE=∠AOE-∠AOC=110°-90°=20°.故答案为:20°.
(2)∠AOD-∠COE=(∠AOC+∠COD)-(∠COD+∠DOE)=∠AOC+∠COD-∠COD-∠DOE=∠AOC-∠DOE=90°-30°=60°.
(3)设∠COE=x.
当OD在OA与OC之间时,∠AOE=∠AOC+∠COE=90°+x,∠COD=∠DOE-∠COE=30°-x.
由题意,得90°+x=4(30°-x),
解得x=6°.
当OD在OC与OB之间时,∠AOE=∠AOC+∠COE=90°+x,∠COD=∠COE-∠DOE=x-30°.
由题意,得90°+x=4(x-30°),
解得x=70°.
综上所述,当∠AOE=4∠COD时,旋转角∠COE的大小为6°或70°.
16.解:(1)△ADF是由△ABE绕点A逆时针旋转90°得到的.
(2)∵△ADF是由△ABE旋转得到的,
∴由图形旋转的性质知∠EBA=∠FDA=90°-70°=20°.
(3)如图,延长BE交DF于点G,则∠AEB=∠DEG.
由(1)可知∠EBA=∠ADF,
∴∠EGD=180°-∠ADF-∠DEG=180°-∠EBA-∠AEB=∠DAB=90°,
∴DF与BE垂直.
又由旋转的性质知DF=BE,
∴DF与BE垂直且相等.
