2021-2022学年冀教版八年级数学下册 21.5一次函数与二元一次方程的关系 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学下册 21.5一次函数与二元一次方程的关系 同步练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 85.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 08:05:37 | ||
图片预览




文档简介
冀教版八年级数学下册第二十一章一次函数与二元一次方程的关系
一、选择题
已知函数和的图象交于点,则关于,的二元一次方程组的解是
A. B. C. D.
若函数与函数的图象交点在第四象限,则的取值范围为
A. B. C. D.
如图,直线与直线交于点,则方程组
A.
B.
C.
D.
一次函数与的图像交点坐标为
A. B. C. D.
如图,一次函数与的图象相交于点,则关于,的二元一次方程组的解是
A. B. . C. D.
一次函数与的图象交点坐标为
A. B. C. D.
一次函数的图象经过点,下列说法错误的是
A. 随的增大而减小 B. 图象不经过第三象限
C. 图象经过点 D. 图象与的图象有一个交点
一次函数与的图像交点坐标为
A. B. C. D.
以方程的解为坐标的点组成的图象是一条直线,这条直线对应的一次函数表达式为
A. B. C. D.
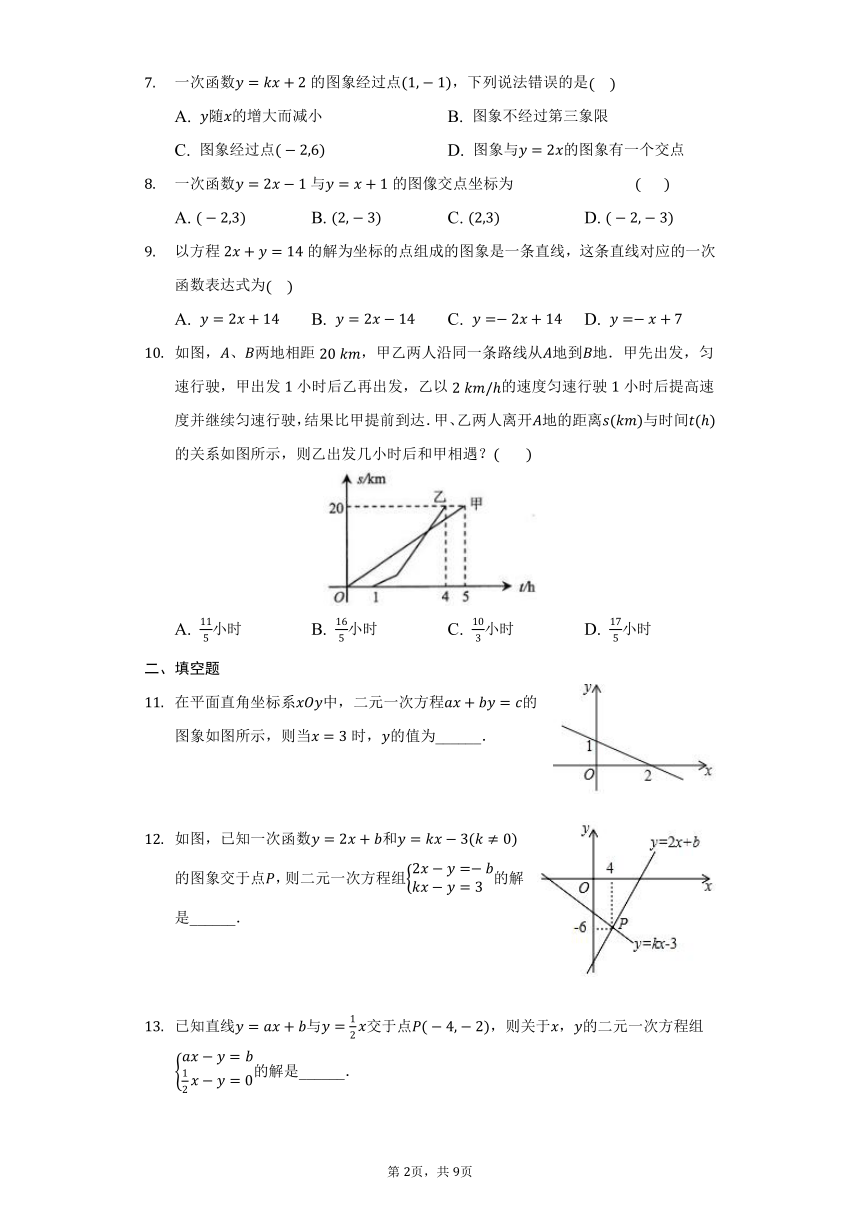
如图,、两地相距,甲乙两人沿同一条路线从地到地.甲先出发,匀速行驶,甲出发小时后乙再出发,乙以的速度匀速行驶小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开地的距离与时间的关系如图所示,则乙出发几小时后和甲相遇?
A. 小时 B. 小时 C. 小时 D. 小时
二、填空题
在平面直角坐标系中,二元一次方程的图象如图所示,则当时,的值为______.
如图,已知一次函数和的图象交于点,则二元一次方程组的解是______.
已知直线与交于点,则关于,的二元一次方程组的解是______.
已知关于、的二元一次方程组的解是,则一次函数和的图像交点坐标为_____.
三、解答题
已知直线经过点,.
求直线的解析式;
若直线与直线相交于点,求点的坐标;
根据图象,写出关于的不等式的解集.
在直角坐标系中直接画出函数的图象;若一次函数的图象分别过点,,请你依据这两个函数的图象写出方程组的解.
如图,直线与轴、轴分别交于点,另一直线与轴、轴分别交于点,两直线相交于点.
求点的坐标;
连接,求的面积.
如图,已知函数和的图象交于点,点的横坐标为,
关于,的方程组的解是______;
______;
求出函数和的图象与轴围成的几何图形的面积.
答案和解析
1.【答案】
【解析】解:函数和的图象交于点,
则关于,的二元一次方程组的解是,
故选:.
2.【答案】
【解析】解:解方程组得:,
即两函数的交点坐标是,
函数与函数的图象交点在第四象限,
,
解得:,
故选:.
3.【答案】
【解析】解:直线与直线交于点,
方程组的解为,
故选:.
4.【答案】
【解析】
解:联立
解得:
函数与的图象的交点坐标为.
故选C.
5.【答案】
【解析】解:把代入得,解得,
所以点坐标为,
所以关于,的二元一次方程组的解是.
故选:.
6.【答案】
【解析】
解:解方程组,得
所以一次函数的图象与的图象的交点坐标是.
故选C.
7.【答案】
【解析】
解:一次函数的图象经过点,
,
解得,
则,
,
则随着的增大而减小,故A正确;
,,
图象经过第一,二,四,不经过第三象限,故B正确;
当时,,
则图象不经过点,故C错误;
解得.
则图象与的图象有一个交点,故D正确.
故选C.
8.【答案】
【解析】
解:联立
解得:
函数与的图象的交点坐标为.
故选C.
9.【答案】
【解析】解:在方程中,
可得:,
所以这条直线对应的一次函数表达式为;
故选C.
10.【答案】
【解析】解:乙提高后的速度为:,
由图象可得:;;
由方程组,解得.
故选:.
11.【答案】
【解析】解:从图象可以得到,
和是二元一次方程的两组解,
,,
,
当时,,
故答案为.
12.【答案】
【解析】解:一次函数和的图象交于点,
点满足二元一次方程组,
方程组的解是.
故答案为.
13.【答案】
【解析】解:直线和直线交点的坐标为,
关于,的二元一次方程组的解是.
故答案为.
直接根据函数图象交点坐标为两函数解析式组成的方程组的解得到答案.
14.【答案】
【解析】解:二元一次方程组的解为
一次函数与的图像的交点坐标为.
故答案为.
15.【答案】解:直线经过点,,
解得
直线的解析式为:;
直线与直线相交于点,
解得
点;
根据图象可得不等式的解集是.
【解析】此题主要考查了待定系数法求一次函数解析式,以及一次函数的交点,一次函数与一元一次不等式的关系,一次函数的图像等知识点,关键是正确从函数图象中获得正确信息.
利用待定系数法把点,代入可得关于、得方程组,再解方程组即可;
联立两个函数解析式,再解方程组即可;
关于的不等式的解集,就是函数的图像在函数图像上边的部分自变量的取值范围,结合两图像交点的横坐标可直接得到答案.
16.【答案】解:当时,
当时,,
一次函数的图象分别过点,,如图:
依据这两个函数的图象可得方程组的解:
.
【解析】本题考查了一次函数的图象以及方程组的解,属于中档题.
分别画出两个函数的图象,依据这两个函数的图象写出方程组的解即可.
17.【答案】解:,解得,故点的坐标.
直线与轴、轴分别交于点,,另一直线与轴、轴分别交于点,,
,,,,,
【解析】与组成方程组,即可求出的坐标.
通过一次函数求出,,,四点的坐标,就可求出面积.
本题考查一次函数的两直线相交的问题,求出与坐标轴的坐标,计算相应的图形的面积.
18.【答案】解:;
;
函数与轴的交点为,
与轴的交点为,
这两个交点之间的距离为,
,
函数和的图象与轴围成的几何图形的面积为:.
第2页,共2页
第1页,共1页
一、选择题
已知函数和的图象交于点,则关于,的二元一次方程组的解是
A. B. C. D.
若函数与函数的图象交点在第四象限,则的取值范围为
A. B. C. D.
如图,直线与直线交于点,则方程组
A.
B.
C.
D.
一次函数与的图像交点坐标为
A. B. C. D.
如图,一次函数与的图象相交于点,则关于,的二元一次方程组的解是
A. B. . C. D.
一次函数与的图象交点坐标为
A. B. C. D.
一次函数的图象经过点,下列说法错误的是
A. 随的增大而减小 B. 图象不经过第三象限
C. 图象经过点 D. 图象与的图象有一个交点
一次函数与的图像交点坐标为
A. B. C. D.
以方程的解为坐标的点组成的图象是一条直线,这条直线对应的一次函数表达式为
A. B. C. D.
如图,、两地相距,甲乙两人沿同一条路线从地到地.甲先出发,匀速行驶,甲出发小时后乙再出发,乙以的速度匀速行驶小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开地的距离与时间的关系如图所示,则乙出发几小时后和甲相遇?
A. 小时 B. 小时 C. 小时 D. 小时
二、填空题
在平面直角坐标系中,二元一次方程的图象如图所示,则当时,的值为______.
如图,已知一次函数和的图象交于点,则二元一次方程组的解是______.
已知直线与交于点,则关于,的二元一次方程组的解是______.
已知关于、的二元一次方程组的解是,则一次函数和的图像交点坐标为_____.
三、解答题
已知直线经过点,.
求直线的解析式;
若直线与直线相交于点,求点的坐标;
根据图象,写出关于的不等式的解集.
在直角坐标系中直接画出函数的图象;若一次函数的图象分别过点,,请你依据这两个函数的图象写出方程组的解.
如图,直线与轴、轴分别交于点,另一直线与轴、轴分别交于点,两直线相交于点.
求点的坐标;
连接,求的面积.
如图,已知函数和的图象交于点,点的横坐标为,
关于,的方程组的解是______;
______;
求出函数和的图象与轴围成的几何图形的面积.
答案和解析
1.【答案】
【解析】解:函数和的图象交于点,
则关于,的二元一次方程组的解是,
故选:.
2.【答案】
【解析】解:解方程组得:,
即两函数的交点坐标是,
函数与函数的图象交点在第四象限,
,
解得:,
故选:.
3.【答案】
【解析】解:直线与直线交于点,
方程组的解为,
故选:.
4.【答案】
【解析】
解:联立
解得:
函数与的图象的交点坐标为.
故选C.
5.【答案】
【解析】解:把代入得,解得,
所以点坐标为,
所以关于,的二元一次方程组的解是.
故选:.
6.【答案】
【解析】
解:解方程组,得
所以一次函数的图象与的图象的交点坐标是.
故选C.
7.【答案】
【解析】
解:一次函数的图象经过点,
,
解得,
则,
,
则随着的增大而减小,故A正确;
,,
图象经过第一,二,四,不经过第三象限,故B正确;
当时,,
则图象不经过点,故C错误;
解得.
则图象与的图象有一个交点,故D正确.
故选C.
8.【答案】
【解析】
解:联立
解得:
函数与的图象的交点坐标为.
故选C.
9.【答案】
【解析】解:在方程中,
可得:,
所以这条直线对应的一次函数表达式为;
故选C.
10.【答案】
【解析】解:乙提高后的速度为:,
由图象可得:;;
由方程组,解得.
故选:.
11.【答案】
【解析】解:从图象可以得到,
和是二元一次方程的两组解,
,,
,
当时,,
故答案为.
12.【答案】
【解析】解:一次函数和的图象交于点,
点满足二元一次方程组,
方程组的解是.
故答案为.
13.【答案】
【解析】解:直线和直线交点的坐标为,
关于,的二元一次方程组的解是.
故答案为.
直接根据函数图象交点坐标为两函数解析式组成的方程组的解得到答案.
14.【答案】
【解析】解:二元一次方程组的解为
一次函数与的图像的交点坐标为.
故答案为.
15.【答案】解:直线经过点,,
解得
直线的解析式为:;
直线与直线相交于点,
解得
点;
根据图象可得不等式的解集是.
【解析】此题主要考查了待定系数法求一次函数解析式,以及一次函数的交点,一次函数与一元一次不等式的关系,一次函数的图像等知识点,关键是正确从函数图象中获得正确信息.
利用待定系数法把点,代入可得关于、得方程组,再解方程组即可;
联立两个函数解析式,再解方程组即可;
关于的不等式的解集,就是函数的图像在函数图像上边的部分自变量的取值范围,结合两图像交点的横坐标可直接得到答案.
16.【答案】解:当时,
当时,,
一次函数的图象分别过点,,如图:
依据这两个函数的图象可得方程组的解:
.
【解析】本题考查了一次函数的图象以及方程组的解,属于中档题.
分别画出两个函数的图象,依据这两个函数的图象写出方程组的解即可.
17.【答案】解:,解得,故点的坐标.
直线与轴、轴分别交于点,,另一直线与轴、轴分别交于点,,
,,,,,
【解析】与组成方程组,即可求出的坐标.
通过一次函数求出,,,四点的坐标,就可求出面积.
本题考查一次函数的两直线相交的问题,求出与坐标轴的坐标,计算相应的图形的面积.
18.【答案】解:;
;
函数与轴的交点为,
与轴的交点为,
这两个交点之间的距离为,
,
函数和的图象与轴围成的几何图形的面积为:.
第2页,共2页
第1页,共1页
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
