2021-2022学年冀教版数学八年级下册21.4一次函数的应用同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年冀教版数学八年级下册21.4一次函数的应用同步练习(word版含解析) | 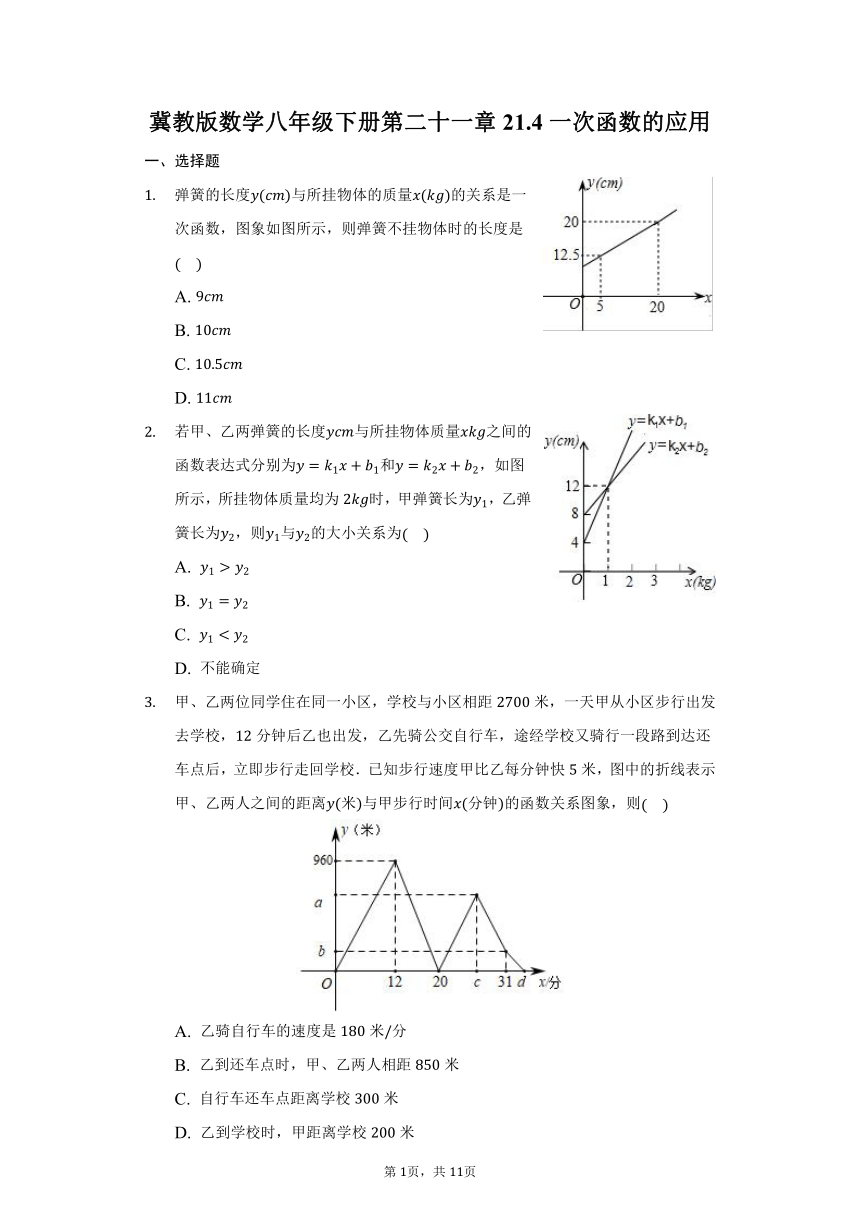 | |
| 格式 | docx | ||
| 文件大小 | 85.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-28 08:07:14 | ||
图片预览





文档简介
冀教版数学八年级下册第二十一章21.4一次函数的应用
一、选择题
弹簧的长度与所挂物体的质量的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是
A.
B.
C.
D.
若甲、乙两弹簧的长度与所挂物体质量之间的函数表达式分别为和,如图所示,所挂物体质量均为时,甲弹簧长为,乙弹簧长为,则与的大小关系为
A.
B.
C.
D. 不能确定
甲、乙两位同学住在同一小区,学校与小区相距米,一天甲从小区步行出发去学校,分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快米,图中的折线表示甲、乙两人之间的距离米与甲步行时间分钟的函数关系图象,则
A. 乙骑自行车的速度是米分
B. 乙到还车点时,甲、乙两人相距米
C. 自行车还车点距离学校米
D. 乙到学校时,甲距离学校米
甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为件甲车间加工的时间为时,与之间的函数图象如图所示,则下列结论错误的是
A. 甲车间每小时加工服装件 B. 这批服装的总件数为件
C. 乙车间每小时加工服装为件 D. 乙车间维修设备用了小时
一家羽毛球馆的打球收费标准为元次,若购买会员年卡,可享受如下优惠:
会员年卡类型 办卡费用元 每次打球收费元
类
类
类
例如,购买类会员卡,一年内打球次,费用为元,若一年内在该羽毛球馆打球的时间介于次之间,则最省钱的方式为
A. 购买类会员年卡 B. 购买类会员年卡
C. 购买类会员年卡 D. 不购买会员年卡
随着“互联网”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用单位:元与行驶里程单位:千米的函数关系如图所示.如果小明某次打车行驶里程为千米,则他的打车费用为
A. 元
B. 元
C. 元
D. 元
长方形的长为、宽为,它的各边都减少,得到的新长方形的周长为,则与之间的关系式是
A. B.
C. D.
郓城大福源超市进了一批花布,出售时要在进价的基础上加一定的利润,其数量米与售价元如下表:
数量米
售价元
下列用数量表示售价的式子中,正确的是
A. B. C. D.
一名老师带领名学生到动物园参观,已知成人票每张元,学生票每张元设门票的总费用为元则与的函数关系式为
A. B. C. D.
某小汽车的油箱可装汽油升,原有汽油升,现再加汽油升。如果每升汽油元,求油箱内汽油的总价元与升之间的函数关系是
A. B.
C. D.
二、填空题
某汽车生产厂对其生产的型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量升与行驶时间小时之间的关系如表:
小时
升
由表格中与的关系可知,当汽车行驶______小时,油箱的余油量为.
如图,在平面直角坐标系中,正方形的边长为,点的坐标为若直线与正方形有两个公共点,则的取值范围是_______.
一根弹簧原长,它所挂物体的质量不超过,并且挂重就伸长,则挂重后弹簧长度关于挂重的关系式为___________________________
为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过立方米时,水价为每立方米元;超过立方米时,超出部分按每立方米元收费,该市每户居民月份用水立方米,应交水费元,则与的关系式为___________.
三、解答题
某农户以元亩的单价承包了亩地种植板栗,每亩种植株优质板栗嫁接苗,购买嫁接苗,购买价格为元株,且每亩地的管理费用为元,一年下来喜获丰收平均每亩板栗产量为,已知当地板栗的批发和;零售价格分别如下表所示:
销售方式 批发 零售
售价元
通过市场调研发现,批发与零售的总销量只能达到总产量的,其中零售量不高于总销售量的,经多方协调当地食品加工厂承诺以元的价格收购该农户余下的板栗,设板栗全部售出后的总利润为元,其中零售.
求与之间的函数关系;
求该农户所收获的最大利润.
总利润总销售额总承包费用购买板栗苗的费用总管理费用
甲、乙两辆汽车沿同一路线从地前往地,甲以千米时的速度匀速行驶,途中出现故障后停车维修,修好后以千米时的速度继续行驶;乙在甲出发小时后匀速前往地,设甲、乙两车与地的路程为千米,甲车离开地的时间为时,与之间的函数图象如图所示.
求和的值.
求两车在途中相遇时的值.
当两车相距千米时,______时.
某商店销售型和型两种型号的电脑,销售一台型电脑可获利元,销售一台型电脑可获利元.该商店计划一次购进两种型号的电脑共台,其中型电脑的进货量不超过型电脑的倍.设购进型电脑台,这台电脑的销售总利润为元.
求与的关系式;
该商店购进型,型电脑各多少台,才能使销售利润最大?
某商场试销一种成本为元的衬衫,规定试销期间,利润不低于成本的,且获利不得高于经试销发现,销售量件与销售单价元有如下对应关系:
售价元件
销量件
试求销售量件与销售单价元之间的函数关系式.
答案和解析
1.【答案】
【解析】解:设与的关系式为,
图象经过,
,
解得:,
,
当时,,
即弹簧不挂物体时的长度是.
故选:.
2.【答案】
【解析】解:点和点在上,
得到方程组:,
解得:,
.
点和点代入上,
得到方程组为,
解得:.
.
当时,,,
.
故选:.
3.【答案】
【解析】解:甲步行的速度为:米分,
乙骑自行车的速度为:米分,
故选项A错误;
乙步行的速度为:米分,
乙全程:,解得,
所以乙骑自行车的路程为:米,
所以自行车还车点距离学校为:米,
故选项C正确;
乙到还车点时,乙的路程为米,甲步行的路程为:米,
此时两人相距:米,
故选项B错误;
乙到学校时,甲的路程为:米,
此时甲离学校:米.
故选项D错误.
故选:.
4.【答案】
【解析】解:由图象可知,甲车间每小时加工零件个数为个,则A正确;
由题意总零件个数为个,则B正确;
乙车间生产速度为个时,则C正确;
乙车间复工后生产时间为小时,故乙车间维修设备时间为小时,则D错误.
故选:.
5.【答案】
【解析】解:设一年内在该游泳馆游泳的次数为次,消费的钱数为元,
根据题意得:
,
,
,
当时,
;
;
;
由此可见,类会员年卡消费最低,所以最省钱的方式为购买类会员年卡.
故选C.
6.【答案】
【解析】解:当行驶里程时,设,
将、代入,得:,
解得:,
,
当时,,
如果小明某次打车行驶里程为千米,则他的打车费用为元.
故选C.
7.【答案】
【解析】解:长方形的长为、宽为,它的各边都减少,得到的新长方形的周长为,
与之间的关系式是:.
故选:.
8.【答案】
【解析】解:根据表格中售价与数量之间的关系可得.
9.【答案】
【解析】略
10.【答案】
【解析】解:原有油的价格是元,
由题意知,总价单价加油体积原有油的价格,
又原有汽油升,
,
.
故选D.
11.【答案】
【解析】解:由表格可知,每行驶小时,耗油升,
时,,
油箱中有油升,
小时,
当行驶小时时,油箱的余油量为,
故答案为.
12.【答案】
【解析】正方形的边长为,点的坐标为,,.
当直线经过点时,,此时.
当直线经过点时,,此时.
所以,直线与正方形有两个公共点,则的取值范围是.
故答案为:.
13.【答案】
【解析】
解:设挂重,则弹簧伸长,
挂重后弹簧长度与挂重之间的关系式是:
14.【答案】
【解析】
解:该市每户居民月份用水立方米,
应交水费元关于的关系式为:.
故答案为:.
15.【答案】解:由题意得
整理得
故与之间的函数关系式为
零售量不高于总销售量的
即:
又,对于而言,随着的增大而增大,
当取最大值时,得最大值为
答:该农户所收获的最大利润为元.
16.【答案】解:,
;
设乙车与地的路程与甲车离开地的时间之间的函数关系式为,
将、代入,
,解得:,
.
当时,.
答:两车在途中相遇时的值为;
或.
【解析】
解:见答案;
见答案;
当时,;
当时,;
当时,.
.
令,即,或,
解得:,舍去,舍去,舍去;
当时,令,解得:.
综上所述:当两车相距千米时,或.
故答案为:或.
【分析】
根据速度路程时间即可求出值,再根据时间路程速度算出到之间的时间段,由此即可求出值;
观察图形找出两点的坐标,利用待定系数法即可求出关于的函数关系式,令即可求出两车相遇的时间;
分、和三段求出关于的函数关系式,二者做差令其绝对值等于即可得出关于的函数绝对值符号的一元一次方程,解之即可求出值,再求出时,中的值.综上即可得出结论.
本题考查了一次函数的应用、待定系数法求函数解析式以及解含绝对值符号的一元一次方程,解题的关键是:根据数量关系列式计算;根据点的坐标利用待定系数法求出函数关系式;根据数量关系求出关于的函数关系式.
17.【答案】解:由题意可得.
商店购进台型电脑和台型电脑的销售利润最大.
18.【答案】解:设销售量件与销售单价元之间的函数关系为,
把、代入,
得,
解得,
即.
经检验,、、均在直线上.
故销售量件与销售单价元之间的函数关系式为.第2页,共2页
第1页,共1页
一、选择题
弹簧的长度与所挂物体的质量的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是
A.
B.
C.
D.
若甲、乙两弹簧的长度与所挂物体质量之间的函数表达式分别为和,如图所示,所挂物体质量均为时,甲弹簧长为,乙弹簧长为,则与的大小关系为
A.
B.
C.
D. 不能确定
甲、乙两位同学住在同一小区,学校与小区相距米,一天甲从小区步行出发去学校,分钟后乙也出发,乙先骑公交自行车,途经学校又骑行一段路到达还车点后,立即步行走回学校.已知步行速度甲比乙每分钟快米,图中的折线表示甲、乙两人之间的距离米与甲步行时间分钟的函数关系图象,则
A. 乙骑自行车的速度是米分
B. 乙到还车点时,甲、乙两人相距米
C. 自行车还车点距离学校米
D. 乙到学校时,甲距离学校米
甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为件甲车间加工的时间为时,与之间的函数图象如图所示,则下列结论错误的是
A. 甲车间每小时加工服装件 B. 这批服装的总件数为件
C. 乙车间每小时加工服装为件 D. 乙车间维修设备用了小时
一家羽毛球馆的打球收费标准为元次,若购买会员年卡,可享受如下优惠:
会员年卡类型 办卡费用元 每次打球收费元
类
类
类
例如,购买类会员卡,一年内打球次,费用为元,若一年内在该羽毛球馆打球的时间介于次之间,则最省钱的方式为
A. 购买类会员年卡 B. 购买类会员年卡
C. 购买类会员年卡 D. 不购买会员年卡
随着“互联网”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用单位:元与行驶里程单位:千米的函数关系如图所示.如果小明某次打车行驶里程为千米,则他的打车费用为
A. 元
B. 元
C. 元
D. 元
长方形的长为、宽为,它的各边都减少,得到的新长方形的周长为,则与之间的关系式是
A. B.
C. D.
郓城大福源超市进了一批花布,出售时要在进价的基础上加一定的利润,其数量米与售价元如下表:
数量米
售价元
下列用数量表示售价的式子中,正确的是
A. B. C. D.
一名老师带领名学生到动物园参观,已知成人票每张元,学生票每张元设门票的总费用为元则与的函数关系式为
A. B. C. D.
某小汽车的油箱可装汽油升,原有汽油升,现再加汽油升。如果每升汽油元,求油箱内汽油的总价元与升之间的函数关系是
A. B.
C. D.
二、填空题
某汽车生产厂对其生产的型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量升与行驶时间小时之间的关系如表:
小时
升
由表格中与的关系可知,当汽车行驶______小时,油箱的余油量为.
如图,在平面直角坐标系中,正方形的边长为,点的坐标为若直线与正方形有两个公共点,则的取值范围是_______.
一根弹簧原长,它所挂物体的质量不超过,并且挂重就伸长,则挂重后弹簧长度关于挂重的关系式为___________________________
为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过立方米时,水价为每立方米元;超过立方米时,超出部分按每立方米元收费,该市每户居民月份用水立方米,应交水费元,则与的关系式为___________.
三、解答题
某农户以元亩的单价承包了亩地种植板栗,每亩种植株优质板栗嫁接苗,购买嫁接苗,购买价格为元株,且每亩地的管理费用为元,一年下来喜获丰收平均每亩板栗产量为,已知当地板栗的批发和;零售价格分别如下表所示:
销售方式 批发 零售
售价元
通过市场调研发现,批发与零售的总销量只能达到总产量的,其中零售量不高于总销售量的,经多方协调当地食品加工厂承诺以元的价格收购该农户余下的板栗,设板栗全部售出后的总利润为元,其中零售.
求与之间的函数关系;
求该农户所收获的最大利润.
总利润总销售额总承包费用购买板栗苗的费用总管理费用
甲、乙两辆汽车沿同一路线从地前往地,甲以千米时的速度匀速行驶,途中出现故障后停车维修,修好后以千米时的速度继续行驶;乙在甲出发小时后匀速前往地,设甲、乙两车与地的路程为千米,甲车离开地的时间为时,与之间的函数图象如图所示.
求和的值.
求两车在途中相遇时的值.
当两车相距千米时,______时.
某商店销售型和型两种型号的电脑,销售一台型电脑可获利元,销售一台型电脑可获利元.该商店计划一次购进两种型号的电脑共台,其中型电脑的进货量不超过型电脑的倍.设购进型电脑台,这台电脑的销售总利润为元.
求与的关系式;
该商店购进型,型电脑各多少台,才能使销售利润最大?
某商场试销一种成本为元的衬衫,规定试销期间,利润不低于成本的,且获利不得高于经试销发现,销售量件与销售单价元有如下对应关系:
售价元件
销量件
试求销售量件与销售单价元之间的函数关系式.
答案和解析
1.【答案】
【解析】解:设与的关系式为,
图象经过,
,
解得:,
,
当时,,
即弹簧不挂物体时的长度是.
故选:.
2.【答案】
【解析】解:点和点在上,
得到方程组:,
解得:,
.
点和点代入上,
得到方程组为,
解得:.
.
当时,,,
.
故选:.
3.【答案】
【解析】解:甲步行的速度为:米分,
乙骑自行车的速度为:米分,
故选项A错误;
乙步行的速度为:米分,
乙全程:,解得,
所以乙骑自行车的路程为:米,
所以自行车还车点距离学校为:米,
故选项C正确;
乙到还车点时,乙的路程为米,甲步行的路程为:米,
此时两人相距:米,
故选项B错误;
乙到学校时,甲的路程为:米,
此时甲离学校:米.
故选项D错误.
故选:.
4.【答案】
【解析】解:由图象可知,甲车间每小时加工零件个数为个,则A正确;
由题意总零件个数为个,则B正确;
乙车间生产速度为个时,则C正确;
乙车间复工后生产时间为小时,故乙车间维修设备时间为小时,则D错误.
故选:.
5.【答案】
【解析】解:设一年内在该游泳馆游泳的次数为次,消费的钱数为元,
根据题意得:
,
,
,
当时,
;
;
;
由此可见,类会员年卡消费最低,所以最省钱的方式为购买类会员年卡.
故选C.
6.【答案】
【解析】解:当行驶里程时,设,
将、代入,得:,
解得:,
,
当时,,
如果小明某次打车行驶里程为千米,则他的打车费用为元.
故选C.
7.【答案】
【解析】解:长方形的长为、宽为,它的各边都减少,得到的新长方形的周长为,
与之间的关系式是:.
故选:.
8.【答案】
【解析】解:根据表格中售价与数量之间的关系可得.
9.【答案】
【解析】略
10.【答案】
【解析】解:原有油的价格是元,
由题意知,总价单价加油体积原有油的价格,
又原有汽油升,
,
.
故选D.
11.【答案】
【解析】解:由表格可知,每行驶小时,耗油升,
时,,
油箱中有油升,
小时,
当行驶小时时,油箱的余油量为,
故答案为.
12.【答案】
【解析】正方形的边长为,点的坐标为,,.
当直线经过点时,,此时.
当直线经过点时,,此时.
所以,直线与正方形有两个公共点,则的取值范围是.
故答案为:.
13.【答案】
【解析】
解:设挂重,则弹簧伸长,
挂重后弹簧长度与挂重之间的关系式是:
14.【答案】
【解析】
解:该市每户居民月份用水立方米,
应交水费元关于的关系式为:.
故答案为:.
15.【答案】解:由题意得
整理得
故与之间的函数关系式为
零售量不高于总销售量的
即:
又,对于而言,随着的增大而增大,
当取最大值时,得最大值为
答:该农户所收获的最大利润为元.
16.【答案】解:,
;
设乙车与地的路程与甲车离开地的时间之间的函数关系式为,
将、代入,
,解得:,
.
当时,.
答:两车在途中相遇时的值为;
或.
【解析】
解:见答案;
见答案;
当时,;
当时,;
当时,.
.
令,即,或,
解得:,舍去,舍去,舍去;
当时,令,解得:.
综上所述:当两车相距千米时,或.
故答案为:或.
【分析】
根据速度路程时间即可求出值,再根据时间路程速度算出到之间的时间段,由此即可求出值;
观察图形找出两点的坐标,利用待定系数法即可求出关于的函数关系式,令即可求出两车相遇的时间;
分、和三段求出关于的函数关系式,二者做差令其绝对值等于即可得出关于的函数绝对值符号的一元一次方程,解之即可求出值,再求出时,中的值.综上即可得出结论.
本题考查了一次函数的应用、待定系数法求函数解析式以及解含绝对值符号的一元一次方程,解题的关键是:根据数量关系列式计算;根据点的坐标利用待定系数法求出函数关系式;根据数量关系求出关于的函数关系式.
17.【答案】解:由题意可得.
商店购进台型电脑和台型电脑的销售利润最大.
18.【答案】解:设销售量件与销售单价元之间的函数关系为,
把、代入,
得,
解得,
即.
经检验,、、均在直线上.
故销售量件与销售单价元之间的函数关系式为.第2页,共2页
第1页,共1页
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
