江苏省通州区三星级高中2012-2013学年高二上学期期中联考数学试题
文档属性
| 名称 | 江苏省通州区三星级高中2012-2013学年高二上学期期中联考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 170.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-21 10:38:20 | ||
图片预览



文档简介
2012—2013学年第一学期通州区三星级高中期中联考
高二数学试题
试题总分:160分 考试时间:120分钟
一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.
1.若圆的一般方程是,则其标准方程为 ▲ .
2.下列四个条件中,能确定一个平面的只有是 ▲ .(填写序号)
①空间中的三点; ②空间中两条直线; ③一条直线和一个点;④两条平行直线.
3.如图所示的直观图,其平面图形的面积为 ▲ .
4.m为任意实数时,直线(m-1)x+(2m-1)y=m-5必过定点 ▲ .
5.一个圆锥的底面直径和高都与同一个球的直径相等,那么圆锥与球
的体积之比是 ▲ .
6.正方体的全面积是a2,它的顶点都在球面上,这个球的表面积是 ▲ .
7.如图,△ABC是直角三角形,ACB=,PA平面ABC,
此图形中有 ▲ 个直角三角形.
8.过点的直线中,被圆截得的弦长最短的直线方程为 ▲ .
9.(文做理不做)正方体中,P、Q、R分别是AB、AD、B1C1的中点.那么正方体的过P、Q、R的截面图形是 ▲ .
(理做文不做)已知空间三个点A(-2,0,2)、B(-1,1,2)和C(-3,0,4),设,.
当实数k为 ▲ 时与互相垂直.
10.如图,已知圆柱形桶的底面半径为6cm,高为cm,有一只蚂蚁
从桶外点出发,经桶的表面通过上口爬行到桶内侧的中点
吃糖,聪明的蚂蚁爬行的最短距离是 ▲ cm.
11.一圆与轴相切,圆心在直线上,且在直线上截得
的弦长为,则此圆的方程为 ▲ .
12.如图,四棱锥S-ABCD底面为正方形,SD底面ABCD,则下列结论中正确的有 ▲ 个.
①AC⊥SB ; ②AB∥平面SCD; ③SA与平面ABCD所成的平面角是∠SAD;
④AB与SC所成的角等于DC与SC所成的角.
13.直线与曲线有且仅有1个公共点,则b的取值范围是 ▲ .
14.如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是 ▲ .
二、解答题:本大题共6小题,共计90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
已知的顶点,边上的高所在直线的方程为,边上中线所在直线的方程为.求直线的方程.
16.(本小题满分14分)
在四面体ABCD中,CB=CD,, E,F分别是AB,BD的点,且AD//平面CEF,
(1)求证: ;
(2)若E是AB的中点,求证:.
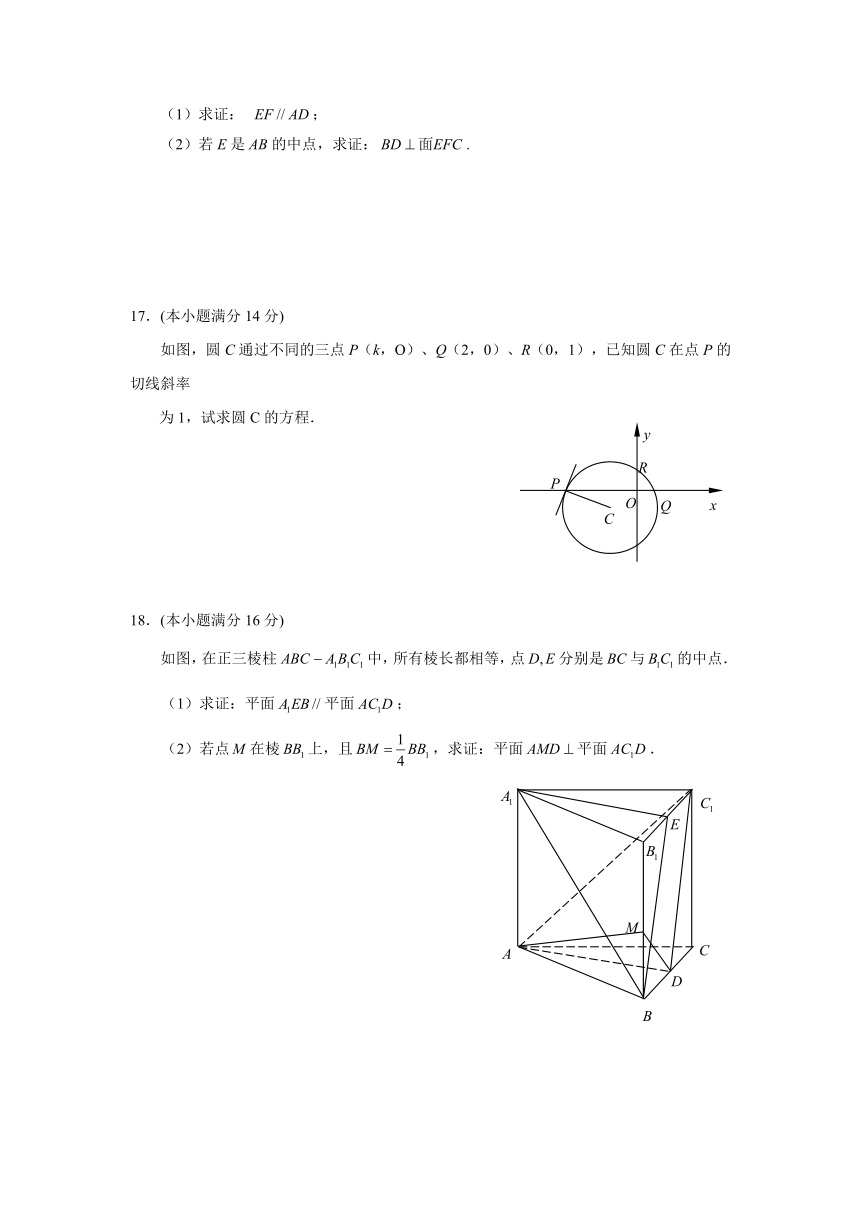
17.(本小题满分14分)
如图,圆C通过不同的三点P(k,O)、Q(2,0)、R(0,1),已知圆C在点P的切线斜率
为1,试求圆C的方程.
18.(本小题满分16分)
如图,在正三棱柱中,所有棱长都相等,点分别是与的中点.
(1)求证:平面平面;
(2)若点在棱上,且,求证:平面平面.
19.(本小题满分16分)
已知圆:.
(1)直线过点,被圆截得的弦长为,求直线的方程;
(2)直线的的斜率为1,且被圆截得弦,若以为直径的圆过原点,求直线的方程.
20.(本小题满分16分)
(文做理不做)已知:正四棱锥S-ABCD的高为,斜高为2,设E为AB中点,F为SC中
点,M为CD边上的点.
(1)求证:EF//平面SAD;
(2)试确定点M的位置,使得平面EFM⊥底面ABCD.
(理做文不做)如图,在四棱锥中,平面.底面为直角梯形,
,,,分别为的中点,点在
棱上,.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)若二面角的大小为,求的值.
2012—2013学年第一学期通州区三星级高中期中联考
高二数学参考答案
一、填空题:本大题共14小题;每小题5分,共70分
1 . 2 . ④ 3 . 4
4 . (9,–4) 5 . 1∶2 6 .
7 . 4 8 .
9 .(文做理不做) 六边形 (理做文不做)
10. 11.或
12. 4 13.
14. 222
提示: 正方体表面面积为25×6-12=138,六道内空(重合部分重复计时)面积为4×5×6=120,重复的小正方体有6个,每个只能算2个小正方形面积,因此要减去面积6×(8-2)=36.
二、解答题:本大题共6小题;共90分.
15. (本小题满分14分)
解:,且直线CE的斜率为
∴直线AB的斜率为-3,
∴直线AB的方程为即……3分
由解得, ∴ ……7分
设,则∴有 ∴……12分
∴直线AC的方程为:即……14分
16. (本小题满分14分)
解:(1) ……7分
(2)
……14分
17.(本小题满分14分)
解:设圆C的方程为,
由于为方程的两根,∴ 即,
又因为圆过点R(0,1),故1+E+F=0, ∴E=-2k-1,
∴圆的方程,圆心C坐标,……7分
∵圆在点P的切线斜率为1 ∴ 解得
∴所求圆的方程为……14分
18.(本小题14分)
解:(1)在正三棱柱ABC-A1B1C1中,因为D,E分别是BC,B1C1的中点,
可知,则为平行四边形,
故从而∥平面
又∴ ∴为平行四边形
∴∥,从而∥平面,
又∴平面∥平面……7分
(2) ∵D是BC的中点,且AB=AC
∴ADBC,又面ABC面, 面ABC面=BC
∴AD面 从而ADDM, AD
∴为二面角的平面角
设正三棱柱的棱长为1,可求
有,∴=
∴平面平面.……14分
⒚(本小题16分)
解: 圆C:,圆心 半径为3,
(1)因直线过点
①当直线斜率不存在时 :
此时被圆截得的弦长为
∴: …… 3分
②当直线斜率存在时
可设方程为 即
由被圆截得的弦长为,则圆心C到的距离为
∴解得
∴方程为 即
由上可知方程为:或 ……8分
(2)设直线的方程为,代入圆C的方程得.
即(*)以AB为直径的圆过原点O,则OA⊥OB.
设,,则, ……10分
即
∴
由(*)式得
∴即,∴或……14分
将或代入(*)方程,对应的△>0.
故直线:或. ……16分
⒛(本小题16分)
解:(文做理不做)
(1)取SD中点G,连结AG,FG,则FG,
∴AEFG为平行四边形,AGEF,进而结论得证. ……6分
(2)连结AC与BD相交点O,取OC中点H,连结SO,FH,EH并延长EH交CD于点M,则SO⊥底面ABCD,FH//SO,
∴FH⊥底面ABCD.∴平面EFM⊥底面ABCD.
由AB//CM知,,∴MC=AE=AB=CD
.∴当点M位于CD的处(距点C)时,平面EFM⊥底面ABCD. ……16分
(理做文不做)
(1)如图建立空间直角坐标系,
∴
设面的法向量
则即∴
令 则
∵ ∴ 又不在面内
∴∥面……6分
(2)由(1)知面的一个法向量,又
∴
∴直线与平面所成角的正弦值为……10分
(3)
设平面的一个法向量为
即
令 则 则=
设平面的一个法向量为
即
令 则 则=
∵二面角的大小为
∴即 解得 或
∴……16分
高二数学试题
试题总分:160分 考试时间:120分钟
一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.
1.若圆的一般方程是,则其标准方程为 ▲ .
2.下列四个条件中,能确定一个平面的只有是 ▲ .(填写序号)
①空间中的三点; ②空间中两条直线; ③一条直线和一个点;④两条平行直线.
3.如图所示的直观图,其平面图形的面积为 ▲ .
4.m为任意实数时,直线(m-1)x+(2m-1)y=m-5必过定点 ▲ .
5.一个圆锥的底面直径和高都与同一个球的直径相等,那么圆锥与球
的体积之比是 ▲ .
6.正方体的全面积是a2,它的顶点都在球面上,这个球的表面积是 ▲ .
7.如图,△ABC是直角三角形,ACB=,PA平面ABC,
此图形中有 ▲ 个直角三角形.
8.过点的直线中,被圆截得的弦长最短的直线方程为 ▲ .
9.(文做理不做)正方体中,P、Q、R分别是AB、AD、B1C1的中点.那么正方体的过P、Q、R的截面图形是 ▲ .
(理做文不做)已知空间三个点A(-2,0,2)、B(-1,1,2)和C(-3,0,4),设,.
当实数k为 ▲ 时与互相垂直.
10.如图,已知圆柱形桶的底面半径为6cm,高为cm,有一只蚂蚁
从桶外点出发,经桶的表面通过上口爬行到桶内侧的中点
吃糖,聪明的蚂蚁爬行的最短距离是 ▲ cm.
11.一圆与轴相切,圆心在直线上,且在直线上截得
的弦长为,则此圆的方程为 ▲ .
12.如图,四棱锥S-ABCD底面为正方形,SD底面ABCD,则下列结论中正确的有 ▲ 个.
①AC⊥SB ; ②AB∥平面SCD; ③SA与平面ABCD所成的平面角是∠SAD;
④AB与SC所成的角等于DC与SC所成的角.
13.直线与曲线有且仅有1个公共点,则b的取值范围是 ▲ .
14.如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是 ▲ .
二、解答题:本大题共6小题,共计90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
已知的顶点,边上的高所在直线的方程为,边上中线所在直线的方程为.求直线的方程.
16.(本小题满分14分)
在四面体ABCD中,CB=CD,, E,F分别是AB,BD的点,且AD//平面CEF,
(1)求证: ;
(2)若E是AB的中点,求证:.
17.(本小题满分14分)
如图,圆C通过不同的三点P(k,O)、Q(2,0)、R(0,1),已知圆C在点P的切线斜率
为1,试求圆C的方程.
18.(本小题满分16分)
如图,在正三棱柱中,所有棱长都相等,点分别是与的中点.
(1)求证:平面平面;
(2)若点在棱上,且,求证:平面平面.
19.(本小题满分16分)
已知圆:.
(1)直线过点,被圆截得的弦长为,求直线的方程;
(2)直线的的斜率为1,且被圆截得弦,若以为直径的圆过原点,求直线的方程.
20.(本小题满分16分)
(文做理不做)已知:正四棱锥S-ABCD的高为,斜高为2,设E为AB中点,F为SC中
点,M为CD边上的点.
(1)求证:EF//平面SAD;
(2)试确定点M的位置,使得平面EFM⊥底面ABCD.
(理做文不做)如图,在四棱锥中,平面.底面为直角梯形,
,,,分别为的中点,点在
棱上,.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)若二面角的大小为,求的值.
2012—2013学年第一学期通州区三星级高中期中联考
高二数学参考答案
一、填空题:本大题共14小题;每小题5分,共70分
1 . 2 . ④ 3 . 4
4 . (9,–4) 5 . 1∶2 6 .
7 . 4 8 .
9 .(文做理不做) 六边形 (理做文不做)
10. 11.或
12. 4 13.
14. 222
提示: 正方体表面面积为25×6-12=138,六道内空(重合部分重复计时)面积为4×5×6=120,重复的小正方体有6个,每个只能算2个小正方形面积,因此要减去面积6×(8-2)=36.
二、解答题:本大题共6小题;共90分.
15. (本小题满分14分)
解:,且直线CE的斜率为
∴直线AB的斜率为-3,
∴直线AB的方程为即……3分
由解得, ∴ ……7分
设,则∴有 ∴……12分
∴直线AC的方程为:即……14分
16. (本小题满分14分)
解:(1) ……7分
(2)
……14分
17.(本小题满分14分)
解:设圆C的方程为,
由于为方程的两根,∴ 即,
又因为圆过点R(0,1),故1+E+F=0, ∴E=-2k-1,
∴圆的方程,圆心C坐标,……7分
∵圆在点P的切线斜率为1 ∴ 解得
∴所求圆的方程为……14分
18.(本小题14分)
解:(1)在正三棱柱ABC-A1B1C1中,因为D,E分别是BC,B1C1的中点,
可知,则为平行四边形,
故从而∥平面
又∴ ∴为平行四边形
∴∥,从而∥平面,
又∴平面∥平面……7分
(2) ∵D是BC的中点,且AB=AC
∴ADBC,又面ABC面, 面ABC面=BC
∴AD面 从而ADDM, AD
∴为二面角的平面角
设正三棱柱的棱长为1,可求
有,∴=
∴平面平面.……14分
⒚(本小题16分)
解: 圆C:,圆心 半径为3,
(1)因直线过点
①当直线斜率不存在时 :
此时被圆截得的弦长为
∴: …… 3分
②当直线斜率存在时
可设方程为 即
由被圆截得的弦长为,则圆心C到的距离为
∴解得
∴方程为 即
由上可知方程为:或 ……8分
(2)设直线的方程为,代入圆C的方程得.
即(*)以AB为直径的圆过原点O,则OA⊥OB.
设,,则, ……10分
即
∴
由(*)式得
∴即,∴或……14分
将或代入(*)方程,对应的△>0.
故直线:或. ……16分
⒛(本小题16分)
解:(文做理不做)
(1)取SD中点G,连结AG,FG,则FG,
∴AEFG为平行四边形,AGEF,进而结论得证. ……6分
(2)连结AC与BD相交点O,取OC中点H,连结SO,FH,EH并延长EH交CD于点M,则SO⊥底面ABCD,FH//SO,
∴FH⊥底面ABCD.∴平面EFM⊥底面ABCD.
由AB//CM知,,∴MC=AE=AB=CD
.∴当点M位于CD的处(距点C)时,平面EFM⊥底面ABCD. ……16分
(理做文不做)
(1)如图建立空间直角坐标系,
∴
设面的法向量
则即∴
令 则
∵ ∴ 又不在面内
∴∥面……6分
(2)由(1)知面的一个法向量,又
∴
∴直线与平面所成角的正弦值为……10分
(3)
设平面的一个法向量为
即
令 则 则=
设平面的一个法向量为
即
令 则 则=
∵二面角的大小为
∴即 解得 或
∴……16分
同课章节目录
