2021-2022学年高一下学期数学北师大版(2019)必修第二册2.4专题:线性运算中的最值问题课件(43张ppt)
文档属性
| 名称 | 2021-2022学年高一下学期数学北师大版(2019)必修第二册2.4专题:线性运算中的最值问题课件(43张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 00:00:00 | ||
图片预览








文档简介
(共43张PPT)
§2.4 线性运算中的最值问题
(专题课)
北师大(2019)必修2
聚焦知识目标
1.了解三角函数是研究周期现象最重要的模型.(重点)
2.初步体会如何利用三角函数研究简单的实际问题.(难点)
线性组合系数或系数代数式的最值问题
数学素养
通过求最值,培养数学抽象及数学运算素养.
向量的线性运算题目中,有一部分是直接运算,有一部分是研究几何性质,还有一部分涉及到最值问题,主要是线性运算系数的最值或范围问题。
1.从系数的多少看,可以把这种专题分为【单 系数最值】【双系数最值】
2.从解题方法上,除了必需要线性运算法则、运算律、定理及特殊结论外,还有【消元法】【基本不等式】【三角换元法】等求最值的方法。
前言
必备向量知识
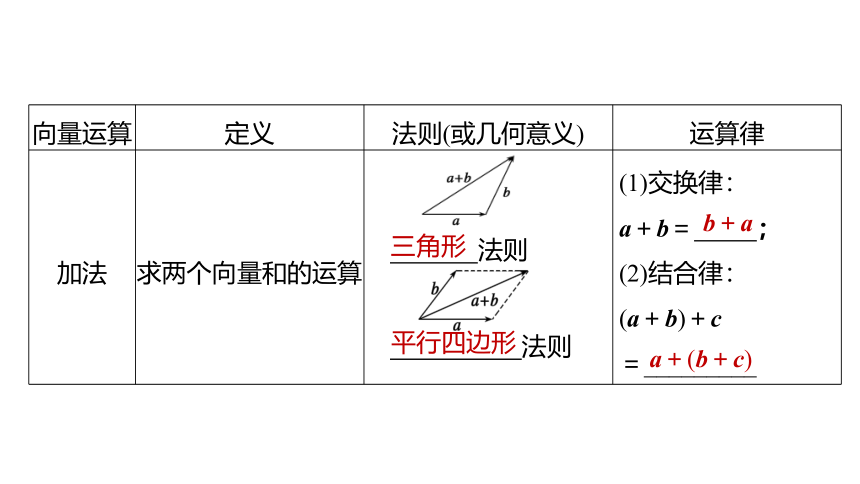
向量运算 定义 法则(或几何意义) 运算律
加法 求两个向量和的运算 法则 法则 (1)交换律:
a+b= ;
(2)结合律:
(a+b)+c
=_________
平行四边形
三角形
b+a
a+(b+c)
减法 求两个向量差的运算 法则 a-b=a+(-b)
数乘 求实数λ与向量a的积的运算 (1)|λa|= ; (2)当λ>0时,λa的方向与a的方向 ;当λ<0时,λa的方向与a的方向 ;当λ=0时,λa=__ (1)λ(μa)= ;
(2)(λ+μ)a= ;
(3)λ(a+b)=_______
三角形
|λ||a|
相同
相反
(λμ)a
λa+μa
λa+λb
0
平面向量的坐标运算
(1)向量加法、减法、数乘及向量的模
设a=(x1,y1),b=(x2,y2),则
a+b= ,a-b= ,
λa= ,|a|= .
平面向量基本定理
如果e1、e2是同一平面内的两个 向量,那么对于这一平面内的任一向量a,存在 一对实数λ1,λ2,使a= .
其中,不共线的向量e1、e2叫作表示这一平面内所有向量的一组 .
不共线
唯一
λ1e1+λ2e2
基底
(x1+x2,y1+y2)
(x1-x2,y1-y2)
(λx1,λy1)
(2)向量坐标的求法
①若向量的起点是坐标原点,则终点坐标即为向量的坐标.
②设A(x1,y1),B(x2,y2),则 = ,
| |= .
平面向量共线的坐标表示
设a=(x1,y1),b=(x2,y2),其中b≠0.a∥b .
(x2-x1,y2-y1)
x1y2-x2y1=0
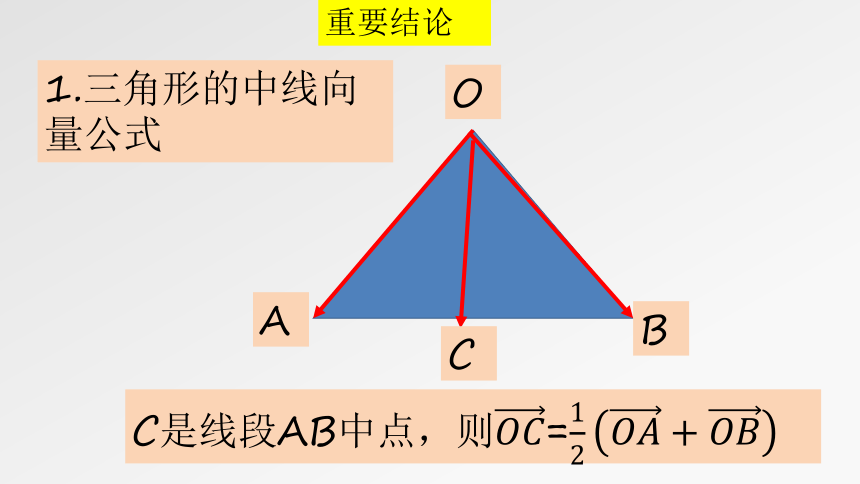
1.三角形的中线向量公式
O
A
B
C
C是线段AB中点,则=
重要结论
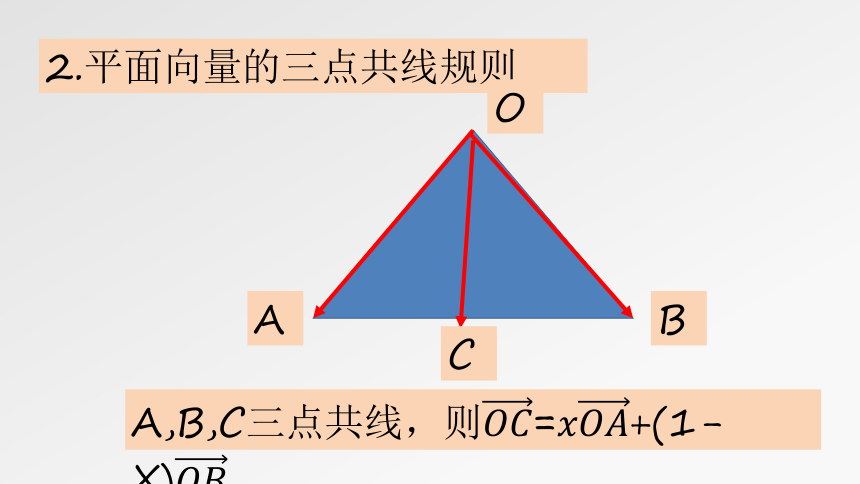
2.平面向量的三点共线规则
O
A
B
C
A,B,C三点共线,则=+(1-X)
O
A
B
C
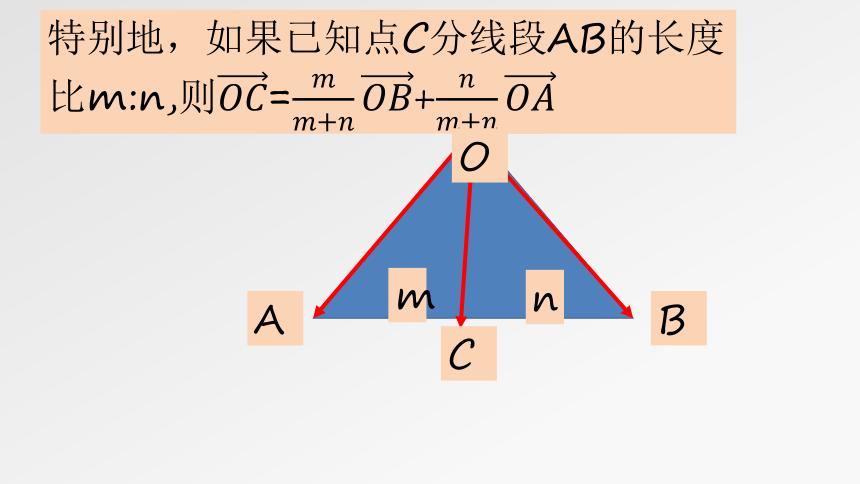
特别地,如果已知点C分线段AB的长度比m:n,则=+
m
n
O
必备函数知识
(1)基本不等式成立的条件: .
(2)等号成立的条件:当且仅当 时取等号.
a≥0,b≥0
a=b
2.几个重要的不等式
(1)a2+b2≥ (a,b∈R).
2ab
2
(3)ab≤ (a,b∈R).
以上不等式等号成立的条件均为a=b.
已知a>0,b>0,a+b=1,则 的最小值为___.
3. 通过常数代换法利用基本不等式
4
∵a>0,b>0,a+b=1,
4. 三角函数值域的不同求法
①利用sin x和cos x的值域直接求;
②把所给的三角函数式变换成y=Asin(ωx+φ)的形式求值域;
③通过换元,转换成二次函数求值域.
进入专题研究
专题导图
单系数最值问题
1.在△ABC中,点D在线段BC的延长线上, 点O在线段CD上(与点C,D不重合),若 ,则x的取值范围是
单系数最值问题
1.在△ABC中,点D在线段BC的延长线上, 点O在线段CD上(与点C,D不重合),若 ,则x的取值范围是
1.,为基底,用【三点共线规则】表示
A
B
C
D
O
2.题设上对照,得到系数
3把系数看作目标函数。是一次函数,就按一次函数求值域思路进行。
思维导图
双系数最值问题
2.已知点E,F分别在正方形ABCD的边BC,CD上运动,且 2,设 若 则x+y的最大值为()
A.2 B.4
1.建系转化为坐标运算
2.不建系,用减法法则运算
3.得到+以用【基本不等式】求x+y最大值
双系数最值问题
2.已知点E,F分别在正方形ABCD的边BC,CD上运动,且 2,设 若 则x+y的最大值为()
A.2 B.4
双系数最值问题
3.已知A,B,P是直线l上三个相异的点,点O∈l,若正实数x,y满足 则的最小值为____.
1.构建【三点共线规则】模型
2.获得2x+y=4
3.用基本不等式知识中的【常量代换法】求目标函数最小值
双系数最值问题
3.已知A,B,P是直线l上三个相异的点,点O∈l,若正实数x,y满足 则的最小值为____.
双系数最值问题
4.如图,A,B,P是圆O上的三点,OP的延长线与线段BA的延长线交于圆0外一点Q,若 求a+b的取值范围.
1.构建【三点共线规则】模型,用 表示.
表示,获得a,b
3.a+b是一个一次函数,直接求值域
双系数最值问题
4.如图,A,B,P是圆O上的三点,OP的延长线与线段BA的延长线交于圆0外一点Q,若 求a+b的取值范围.
双系数最值问题
5. ABC中,D为AC上一点,满足 若P为BD上一点,满足 ).则mn的最大值为___,+ 的最小值为____.
1.典型的【三点共线向量规则】的应用,获得m+4n=1
2.用算术平均数与几何平均数关系求出mn最大值
3.用【常量代换法】求出+ 最小值
双系数最值问题
5. ABC中,D为AC上一点,满足 若P为BD上一点,满足 ).则mn的最大值为___,+ 的最小值为____.
双系数最值问题
6. ABC中,D为AC上一点,满足 若P为BD上一点,满足 ).则mn的最大值为___,+ 的最小值为____.
双系数最值问题
7.矩形ABCD中,AB=2,AD=1,E为DC边的中点,P为线段AE上的动点,设向量 (λ,μ∈R),求λ+μ的最大值.
1.由于有动点,且在矩形中运动,适合建系
2.对所给向量关系运算出λ,μ
3. λ+μ成为一次函数
双系数最值问题
7.矩形ABCD中,AB=2,AD=1,E为DC边的中点,P为线段AE上的动点,设向量 (λ,μ∈R),求λ+μ的最大值.
双系数最值问题
8.已知向量m=(a,-1),n=(2b-1、3)(a>0,b>0),若m//n,则的最小值为()
12
C. 15
1.用坐标表示,显得关系非常明
2.依向量平行关系,求出3a+2b=1
3.用【常量代换法】求出目标最小值
双系数最值问题
8.已知向量m=(a,-1),n=(2b-1、3)(a>0,b>0),若m//n,则的最小值为()
12
C. 15
双系数最值问题
9.向量a=(1,x),b=(x,y-2),其中x>0,若a与b共线,则最小值为_
1.平行关系坐标运算
2.成为对勾函数,用基本不等式可得最小值
双系数最值问题
9.向量a=(1,x),b=(x,y-2),其中x>0,若a与b共线,则最小值为_
双系数最值问题
10.
1.用坐标表示,显得关系非常明
2.依向量平行关系,求出2a+b=1
3.用【常量代换法】求出目标最小值
双系数最值问题
10.
双系数最值问题
11.
1.通过向量平行的坐标运算,得到用t的三角表达
2.代入目标函数得到关于cosθ的二次函数
3.参考【三角换元法】求最小值
双系数最值问题
11.
双系数最值问题
12.
如图所示,A,B,C是圆O上的三点,线段CO的延长线与BA的延长线交于圆O外的一点D,若 ,则m+n的取值范围是______.
1.符合【三点共线向量规则】
2.符合共线关系
3.示完后,发现m+n是一次函数
双系数最值问题
12.
如图所示,A,B,C是圆O上的三点,线段CO的延长线与BA的延长线交于圆O外的一点D,若 ,则m+n的取值范围是______.
∴m=kλ,n=k(1-λ),
∴m+n=k,从而m+n∈(-1,0).
§2.4 线性运算中的最值问题
(专题课)
北师大(2019)必修2
聚焦知识目标
1.了解三角函数是研究周期现象最重要的模型.(重点)
2.初步体会如何利用三角函数研究简单的实际问题.(难点)
线性组合系数或系数代数式的最值问题
数学素养
通过求最值,培养数学抽象及数学运算素养.
向量的线性运算题目中,有一部分是直接运算,有一部分是研究几何性质,还有一部分涉及到最值问题,主要是线性运算系数的最值或范围问题。
1.从系数的多少看,可以把这种专题分为【单 系数最值】【双系数最值】
2.从解题方法上,除了必需要线性运算法则、运算律、定理及特殊结论外,还有【消元法】【基本不等式】【三角换元法】等求最值的方法。
前言
必备向量知识
向量运算 定义 法则(或几何意义) 运算律
加法 求两个向量和的运算 法则 法则 (1)交换律:
a+b= ;
(2)结合律:
(a+b)+c
=_________
平行四边形
三角形
b+a
a+(b+c)
减法 求两个向量差的运算 法则 a-b=a+(-b)
数乘 求实数λ与向量a的积的运算 (1)|λa|= ; (2)当λ>0时,λa的方向与a的方向 ;当λ<0时,λa的方向与a的方向 ;当λ=0时,λa=__ (1)λ(μa)= ;
(2)(λ+μ)a= ;
(3)λ(a+b)=_______
三角形
|λ||a|
相同
相反
(λμ)a
λa+μa
λa+λb
0
平面向量的坐标运算
(1)向量加法、减法、数乘及向量的模
设a=(x1,y1),b=(x2,y2),则
a+b= ,a-b= ,
λa= ,|a|= .
平面向量基本定理
如果e1、e2是同一平面内的两个 向量,那么对于这一平面内的任一向量a,存在 一对实数λ1,λ2,使a= .
其中,不共线的向量e1、e2叫作表示这一平面内所有向量的一组 .
不共线
唯一
λ1e1+λ2e2
基底
(x1+x2,y1+y2)
(x1-x2,y1-y2)
(λx1,λy1)
(2)向量坐标的求法
①若向量的起点是坐标原点,则终点坐标即为向量的坐标.
②设A(x1,y1),B(x2,y2),则 = ,
| |= .
平面向量共线的坐标表示
设a=(x1,y1),b=(x2,y2),其中b≠0.a∥b .
(x2-x1,y2-y1)
x1y2-x2y1=0
1.三角形的中线向量公式
O
A
B
C
C是线段AB中点,则=
重要结论
2.平面向量的三点共线规则
O
A
B
C
A,B,C三点共线,则=+(1-X)
O
A
B
C
特别地,如果已知点C分线段AB的长度比m:n,则=+
m
n
O
必备函数知识
(1)基本不等式成立的条件: .
(2)等号成立的条件:当且仅当 时取等号.
a≥0,b≥0
a=b
2.几个重要的不等式
(1)a2+b2≥ (a,b∈R).
2ab
2
(3)ab≤ (a,b∈R).
以上不等式等号成立的条件均为a=b.
已知a>0,b>0,a+b=1,则 的最小值为___.
3. 通过常数代换法利用基本不等式
4
∵a>0,b>0,a+b=1,
4. 三角函数值域的不同求法
①利用sin x和cos x的值域直接求;
②把所给的三角函数式变换成y=Asin(ωx+φ)的形式求值域;
③通过换元,转换成二次函数求值域.
进入专题研究
专题导图
单系数最值问题
1.在△ABC中,点D在线段BC的延长线上, 点O在线段CD上(与点C,D不重合),若 ,则x的取值范围是
单系数最值问题
1.在△ABC中,点D在线段BC的延长线上, 点O在线段CD上(与点C,D不重合),若 ,则x的取值范围是
1.,为基底,用【三点共线规则】表示
A
B
C
D
O
2.题设上对照,得到系数
3把系数看作目标函数。是一次函数,就按一次函数求值域思路进行。
思维导图
双系数最值问题
2.已知点E,F分别在正方形ABCD的边BC,CD上运动,且 2,设 若 则x+y的最大值为()
A.2 B.4
1.建系转化为坐标运算
2.不建系,用减法法则运算
3.得到+以用【基本不等式】求x+y最大值
双系数最值问题
2.已知点E,F分别在正方形ABCD的边BC,CD上运动,且 2,设 若 则x+y的最大值为()
A.2 B.4
双系数最值问题
3.已知A,B,P是直线l上三个相异的点,点O∈l,若正实数x,y满足 则的最小值为____.
1.构建【三点共线规则】模型
2.获得2x+y=4
3.用基本不等式知识中的【常量代换法】求目标函数最小值
双系数最值问题
3.已知A,B,P是直线l上三个相异的点,点O∈l,若正实数x,y满足 则的最小值为____.
双系数最值问题
4.如图,A,B,P是圆O上的三点,OP的延长线与线段BA的延长线交于圆0外一点Q,若 求a+b的取值范围.
1.构建【三点共线规则】模型,用 表示.
表示,获得a,b
3.a+b是一个一次函数,直接求值域
双系数最值问题
4.如图,A,B,P是圆O上的三点,OP的延长线与线段BA的延长线交于圆0外一点Q,若 求a+b的取值范围.
双系数最值问题
5. ABC中,D为AC上一点,满足 若P为BD上一点,满足 ).则mn的最大值为___,+ 的最小值为____.
1.典型的【三点共线向量规则】的应用,获得m+4n=1
2.用算术平均数与几何平均数关系求出mn最大值
3.用【常量代换法】求出+ 最小值
双系数最值问题
5. ABC中,D为AC上一点,满足 若P为BD上一点,满足 ).则mn的最大值为___,+ 的最小值为____.
双系数最值问题
6. ABC中,D为AC上一点,满足 若P为BD上一点,满足 ).则mn的最大值为___,+ 的最小值为____.
双系数最值问题
7.矩形ABCD中,AB=2,AD=1,E为DC边的中点,P为线段AE上的动点,设向量 (λ,μ∈R),求λ+μ的最大值.
1.由于有动点,且在矩形中运动,适合建系
2.对所给向量关系运算出λ,μ
3. λ+μ成为一次函数
双系数最值问题
7.矩形ABCD中,AB=2,AD=1,E为DC边的中点,P为线段AE上的动点,设向量 (λ,μ∈R),求λ+μ的最大值.
双系数最值问题
8.已知向量m=(a,-1),n=(2b-1、3)(a>0,b>0),若m//n,则的最小值为()
12
C. 15
1.用坐标表示,显得关系非常明
2.依向量平行关系,求出3a+2b=1
3.用【常量代换法】求出目标最小值
双系数最值问题
8.已知向量m=(a,-1),n=(2b-1、3)(a>0,b>0),若m//n,则的最小值为()
12
C. 15
双系数最值问题
9.向量a=(1,x),b=(x,y-2),其中x>0,若a与b共线,则最小值为_
1.平行关系坐标运算
2.成为对勾函数,用基本不等式可得最小值
双系数最值问题
9.向量a=(1,x),b=(x,y-2),其中x>0,若a与b共线,则最小值为_
双系数最值问题
10.
1.用坐标表示,显得关系非常明
2.依向量平行关系,求出2a+b=1
3.用【常量代换法】求出目标最小值
双系数最值问题
10.
双系数最值问题
11.
1.通过向量平行的坐标运算,得到用t的三角表达
2.代入目标函数得到关于cosθ的二次函数
3.参考【三角换元法】求最小值
双系数最值问题
11.
双系数最值问题
12.
如图所示,A,B,C是圆O上的三点,线段CO的延长线与BA的延长线交于圆O外的一点D,若 ,则m+n的取值范围是______.
1.符合【三点共线向量规则】
2.符合共线关系
3.示完后,发现m+n是一次函数
双系数最值问题
12.
如图所示,A,B,C是圆O上的三点,线段CO的延长线与BA的延长线交于圆O外的一点D,若 ,则m+n的取值范围是______.
∴m=kλ,n=k(1-λ),
∴m+n=k,从而m+n∈(-1,0).
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
