2021-2022学年高一下学期数学沪教版(2020)必修第二册6.1.3 任意角的正弦、余弦、正切、余切(1)测试题word版含答案
文档属性
| 名称 | 2021-2022学年高一下学期数学沪教版(2020)必修第二册6.1.3 任意角的正弦、余弦、正切、余切(1)测试题word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 204.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-29 18:09:22 | ||
图片预览



文档简介
【学生版】
《第 6 章 三角》【6.1.3 任意角的正弦、余弦、正切、余切(1)】
一、选择题(每小题6分,共12分)
1、已知角α的终边过点P(-1,2),则cos α的值为( )
A.- B.- C. D.
【提示】
【答案】
【解析】
【考点】
2、已知sin α=,cos α=-,则角α所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【提示】
【答案】
【解析】
【考点】
二、填充题(每小题10分,共60分)
3、如果角α的终边过点P(2sin30°,-2cos30°),则sinα的值等于
4、设角α的终边上有一点P(4,-3),则2sin α+cos α的值是
5、已知P(-2,y)是角α终边上一点,且sin α=-,则cos α=________
6、当α为第四象限时,-的值是____________.
7、若角α的终边与单位圆相交于点,则sin α的值为
8、若三角形的两内角α,β满足sin α·cos β<0,则此三角形必为 三角形。
三、解答题(第9题12分,第10题16分)
9、已知角θ的终边上有一点P(x,3)(x≠0),且cos θ=x,求:sin θ+tan θ的值
10、角θ的终边落在直线y=2x上,求sin θ,cos θ的值.
【附录】相关考点
考点一 角α的正弦、 余弦、 正切、 余切 对于任意角α来说, 设P(x,y)是α终边上异于原点的任意一点,, 称为角α的正弦,记作sin α; 称为角α的余弦,记作cos α, 因此sin α=,cos α=; 当角α的终边不在y轴上时, 称为角α的正切,记作tan α,即tan α=, 称为角α的正切,记作cot α,即cot=; 角α的正弦、余弦、正切、余切都称为α的三角函数; 还有正割()、余割(α);
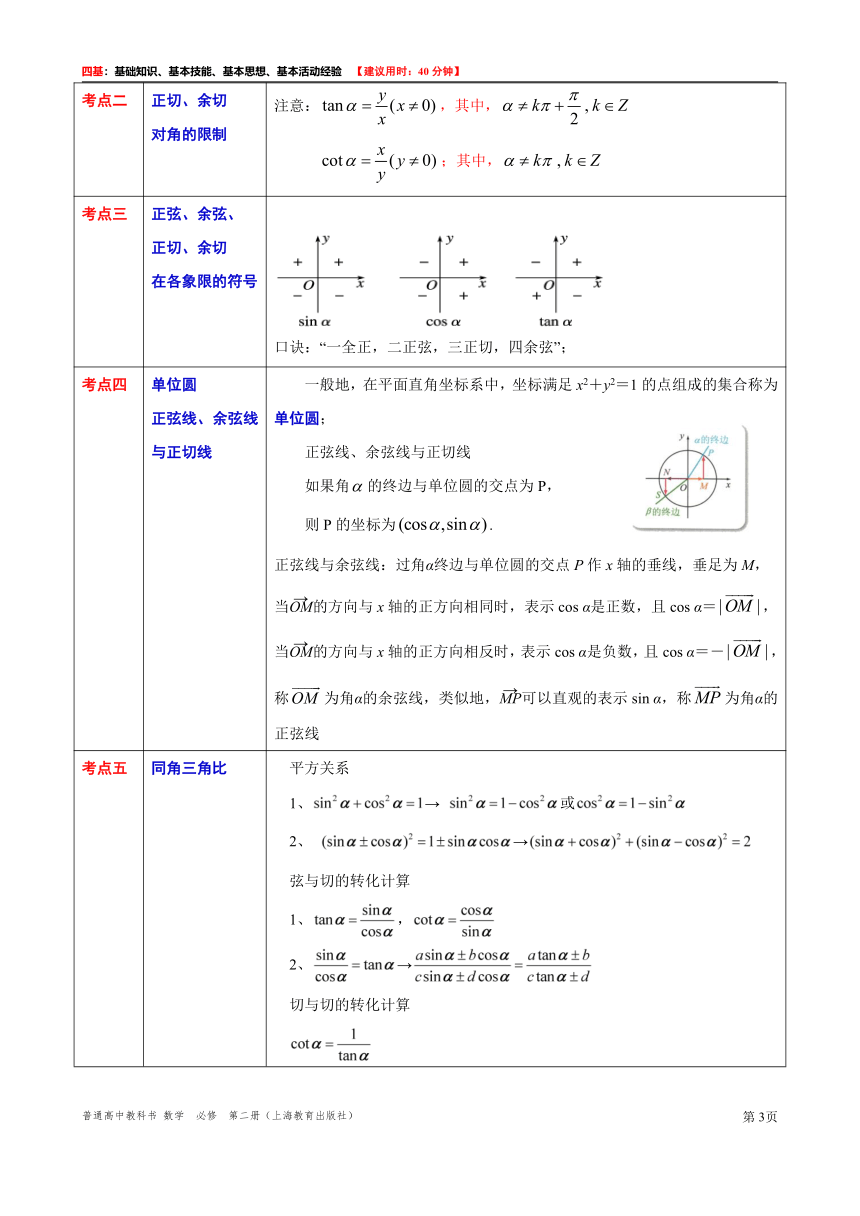
考点二 正切、余切 对角的限制 注意:,其中, ;其中,
考点三 正弦、余弦、 正切、余切 在各象限的符号 口诀:“一全正,二正弦,三正切,四余弦”;
考点四 单位圆 正弦线、余弦线与正切线 一般地,在平面直角坐标系中,坐标满足x2+y2=1的点组成的集合称为单位圆; 正弦线、余弦线与正切线 如果角的终边与单位圆的交点为P, 则P的坐标为. 正弦线与余弦线:过角α终边与单位圆的交点P作x轴的垂线,垂足为M, 当的方向与x轴的正方向相同时,表示cos α是正数,且cos α=, 当的方向与x轴的正方向相反时,表示cos α是负数,且cos α=-, 称为角α的余弦线,类似地,可以直观的表示sin α,称为角α的正弦线
考点五 同角三角比 平方关系 1、→ 或 2、 → 弦与切的转化计算 1、, 2、→ 切与切的转化计算
【教师版】
《第 6 章 三角》【6.1.3 任意角的正弦、余弦、正切、余切(1)】
一、选择题(每小题6分,共12分)
1、已知角α的终边过点P(-1,2),则cos α的值为( )
A.- B.- C. D.
【提示】注意:任意角三角比定义的前提;
【答案】A;
【解析】由题意得:r==,cos α==-;
【考点】任意角α的三角比的定义;
2、已知sin α=,cos α=-,则角α所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【提示】注意:三角比的符号规则;
【答案】B;
【解析】由sin α>0得角α的终边在第一或第二象限;由cos α<0得角α的终边在第二或第三象限.综上,角α所在的象限是第二象限;
【考点】任意角三角比的符号规则,与交集的简单交汇;
二、填充题(每小题10分,共60分)
3、如果角α的终边过点P(2sin30°,-2cos30°),则sinα的值等于
【提示】注意:任意角三角比定义;
【答案】-;
【解析】由题意得P(1,-),它与原点的距离r==2,所以sinα=-;
【考点】任意角α的三角比的定义;
4、设角α的终边上有一点P(4,-3),则2sin α+cos α的值是
【提示】注意:任意角三角比定义;
【答案】-;
【解析】由三角函数的定义可知sin α==-,cos α==,
所以2sin α+cos α=2×+=-;
【考点】任意角α的三角比的定义;
5、已知P(-2,y)是角α终边上一点,且sin α=-,则cos α=________
【提示】注意:任意角三角比定义;
【答案】-;
【解析】因为r=,所以sin α===-,所以y<0,所以y=-1,r=,
所以cos α===-;
【考点】任意角α的三角比的定义;求任意角的三角函数值的两种方法
第一步,根据定义,在角α的终边上任取一点P(x,y)(P与原点O不重合);
第二步,计算r:r=|OP|=(r>0);
第三步,求值:由sin α=,cos α=求值
6、当α为第四象限时,-的值是____________.
【提示】注意:任意角的三角比的符号;
【答案】-2;
【解析】因为α为第四象限角,所以=-1,=1.所以-=-1-1=-2;
【考点】任意角的三角比的符号;与绝对值的简单交汇;
7、若角α的终边与单位圆相交于点,则sin α的值为
【提示】注意:单位圆;
【答案】-;
【解析】利用任意角三角函数的定义可知,点到原点的距离为1,则sin α==-;
【考点】任意角的三角比、单位圆;注意:利用单位圆简化计算;
8、若三角形的两内角α,β满足sin α·cos β<0,则此三角形必为 三角形。
【提示】注意:三角形内角的限制条件;
【答案】钝角;
【解析】三角形的两内角α,β的终边一定落在第一、二象限或y轴正半轴上,sin α·cos β <0,所以sin α>0,cos β <0,所以角β为钝角,此三角形为钝角三角形;
【考点】任意角的三角比的符号;与三角形内角的限制条件进行了简单的交汇;
三、解答题(第9题12分,第10题16分)
9、已知角θ的终边上有一点P(x,3)(x≠0),且cos θ=x,求:sin θ+tan θ的值
【提示】注意:“终边上有一点P(x,3)”;
【答案】或;
【解析】因为r= ,cos θ=,所以x= ;
又x≠0,所以x=±1,所以r=.又y=3>0,所以θ是第一或第二象限角.
当θ为第一象限角时,sin θ=,tan θ=3;则sin θ+tan θ=.
当θ为第二象限角时,sin θ=,tan θ=-3.则sin θ+tan θ=.
【考点】任意角的三角比的定义、符号规则;与“平方开方”代数运算进行了简单交汇;
10、角θ的终边落在直线y=2x上,求sin θ,cos θ的值.
【提示】注意:分类讨论
【解析】①若θ的终边在第一象限内,设点P(a,2a)(a>0)是其终边上任意一点,
因为r=|OP|==a,所以sin θ===,cos θ===.
②若θ的终边在第三象限内,设点P(a,2a)(a<0)是其终边上任意一点,
因为r=|OP|==-a(a<0),
所以sin θ===-,cos θ===-.
【考点】任意角的三角比的定义、符号规则;与“平方开方”代数运算进行了简单交汇;
【附录】相关考点
考点一 角α的正弦、 余弦、 正切、 余切 对于任意角α来说, 设P(x,y)是α终边上异于原点的任意一点,, 称为角α的正弦,记作sin α; 称为角α的余弦,记作cos α, 因此sin α=,cos α=; 当角α的终边不在y轴上时, 称为角α的正切,记作tan α,即tan α=, 称为角α的正切,记作cot α,即cot=; 角α的正弦、余弦、正切、余切都称为α的三角函数; 还有正割()、余割(α);
考点二 正切、余切 对角的限制 注意:,其中, ;其中,
考点三 正弦、余弦、 正切、余切 在各象限的符号 口诀:“一全正,二正弦,三正切,四余弦”;
考点四 单位圆 正弦线、余弦线与正切线 一般地,在平面直角坐标系中,坐标满足x2+y2=1的点组成的集合称为单位圆; 正弦线、余弦线与正切线 如果角的终边与单位圆的交点为P, 则P的坐标为. 正弦线与余弦线:过角α终边与单位圆的交点P作x轴的垂线,垂足为M, 当的方向与x轴的正方向相同时,表示cos α是正数,且cos α=, 当的方向与x轴的正方向相反时,表示cos α是负数,且cos α=-, 称为角α的余弦线,类似地,可以直观的表示sin α,称为角α的正弦线
考点五 同角三角比 平方关系 1、→ 或 2、 → 弦与切的转化计算 1、, 2、→ 切与切的转化计算
四基:基础知识、基本技能、基本思想、基本活动经验 【建议用时:40分钟】
第1页
普通高中教科书 数学 必修 第二册(上海教育出版社)
《第 6 章 三角》【6.1.3 任意角的正弦、余弦、正切、余切(1)】
一、选择题(每小题6分,共12分)
1、已知角α的终边过点P(-1,2),则cos α的值为( )
A.- B.- C. D.
【提示】
【答案】
【解析】
【考点】
2、已知sin α=,cos α=-,则角α所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【提示】
【答案】
【解析】
【考点】
二、填充题(每小题10分,共60分)
3、如果角α的终边过点P(2sin30°,-2cos30°),则sinα的值等于
4、设角α的终边上有一点P(4,-3),则2sin α+cos α的值是
5、已知P(-2,y)是角α终边上一点,且sin α=-,则cos α=________
6、当α为第四象限时,-的值是____________.
7、若角α的终边与单位圆相交于点,则sin α的值为
8、若三角形的两内角α,β满足sin α·cos β<0,则此三角形必为 三角形。
三、解答题(第9题12分,第10题16分)
9、已知角θ的终边上有一点P(x,3)(x≠0),且cos θ=x,求:sin θ+tan θ的值
10、角θ的终边落在直线y=2x上,求sin θ,cos θ的值.
【附录】相关考点
考点一 角α的正弦、 余弦、 正切、 余切 对于任意角α来说, 设P(x,y)是α终边上异于原点的任意一点,, 称为角α的正弦,记作sin α; 称为角α的余弦,记作cos α, 因此sin α=,cos α=; 当角α的终边不在y轴上时, 称为角α的正切,记作tan α,即tan α=, 称为角α的正切,记作cot α,即cot=; 角α的正弦、余弦、正切、余切都称为α的三角函数; 还有正割()、余割(α);
考点二 正切、余切 对角的限制 注意:,其中, ;其中,
考点三 正弦、余弦、 正切、余切 在各象限的符号 口诀:“一全正,二正弦,三正切,四余弦”;
考点四 单位圆 正弦线、余弦线与正切线 一般地,在平面直角坐标系中,坐标满足x2+y2=1的点组成的集合称为单位圆; 正弦线、余弦线与正切线 如果角的终边与单位圆的交点为P, 则P的坐标为. 正弦线与余弦线:过角α终边与单位圆的交点P作x轴的垂线,垂足为M, 当的方向与x轴的正方向相同时,表示cos α是正数,且cos α=, 当的方向与x轴的正方向相反时,表示cos α是负数,且cos α=-, 称为角α的余弦线,类似地,可以直观的表示sin α,称为角α的正弦线
考点五 同角三角比 平方关系 1、→ 或 2、 → 弦与切的转化计算 1、, 2、→ 切与切的转化计算
【教师版】
《第 6 章 三角》【6.1.3 任意角的正弦、余弦、正切、余切(1)】
一、选择题(每小题6分,共12分)
1、已知角α的终边过点P(-1,2),则cos α的值为( )
A.- B.- C. D.
【提示】注意:任意角三角比定义的前提;
【答案】A;
【解析】由题意得:r==,cos α==-;
【考点】任意角α的三角比的定义;
2、已知sin α=,cos α=-,则角α所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【提示】注意:三角比的符号规则;
【答案】B;
【解析】由sin α>0得角α的终边在第一或第二象限;由cos α<0得角α的终边在第二或第三象限.综上,角α所在的象限是第二象限;
【考点】任意角三角比的符号规则,与交集的简单交汇;
二、填充题(每小题10分,共60分)
3、如果角α的终边过点P(2sin30°,-2cos30°),则sinα的值等于
【提示】注意:任意角三角比定义;
【答案】-;
【解析】由题意得P(1,-),它与原点的距离r==2,所以sinα=-;
【考点】任意角α的三角比的定义;
4、设角α的终边上有一点P(4,-3),则2sin α+cos α的值是
【提示】注意:任意角三角比定义;
【答案】-;
【解析】由三角函数的定义可知sin α==-,cos α==,
所以2sin α+cos α=2×+=-;
【考点】任意角α的三角比的定义;
5、已知P(-2,y)是角α终边上一点,且sin α=-,则cos α=________
【提示】注意:任意角三角比定义;
【答案】-;
【解析】因为r=,所以sin α===-,所以y<0,所以y=-1,r=,
所以cos α===-;
【考点】任意角α的三角比的定义;求任意角的三角函数值的两种方法
第一步,根据定义,在角α的终边上任取一点P(x,y)(P与原点O不重合);
第二步,计算r:r=|OP|=(r>0);
第三步,求值:由sin α=,cos α=求值
6、当α为第四象限时,-的值是____________.
【提示】注意:任意角的三角比的符号;
【答案】-2;
【解析】因为α为第四象限角,所以=-1,=1.所以-=-1-1=-2;
【考点】任意角的三角比的符号;与绝对值的简单交汇;
7、若角α的终边与单位圆相交于点,则sin α的值为
【提示】注意:单位圆;
【答案】-;
【解析】利用任意角三角函数的定义可知,点到原点的距离为1,则sin α==-;
【考点】任意角的三角比、单位圆;注意:利用单位圆简化计算;
8、若三角形的两内角α,β满足sin α·cos β<0,则此三角形必为 三角形。
【提示】注意:三角形内角的限制条件;
【答案】钝角;
【解析】三角形的两内角α,β的终边一定落在第一、二象限或y轴正半轴上,sin α·cos β <0,所以sin α>0,cos β <0,所以角β为钝角,此三角形为钝角三角形;
【考点】任意角的三角比的符号;与三角形内角的限制条件进行了简单的交汇;
三、解答题(第9题12分,第10题16分)
9、已知角θ的终边上有一点P(x,3)(x≠0),且cos θ=x,求:sin θ+tan θ的值
【提示】注意:“终边上有一点P(x,3)”;
【答案】或;
【解析】因为r= ,cos θ=,所以x= ;
又x≠0,所以x=±1,所以r=.又y=3>0,所以θ是第一或第二象限角.
当θ为第一象限角时,sin θ=,tan θ=3;则sin θ+tan θ=.
当θ为第二象限角时,sin θ=,tan θ=-3.则sin θ+tan θ=.
【考点】任意角的三角比的定义、符号规则;与“平方开方”代数运算进行了简单交汇;
10、角θ的终边落在直线y=2x上,求sin θ,cos θ的值.
【提示】注意:分类讨论
【解析】①若θ的终边在第一象限内,设点P(a,2a)(a>0)是其终边上任意一点,
因为r=|OP|==a,所以sin θ===,cos θ===.
②若θ的终边在第三象限内,设点P(a,2a)(a<0)是其终边上任意一点,
因为r=|OP|==-a(a<0),
所以sin θ===-,cos θ===-.
【考点】任意角的三角比的定义、符号规则;与“平方开方”代数运算进行了简单交汇;
【附录】相关考点
考点一 角α的正弦、 余弦、 正切、 余切 对于任意角α来说, 设P(x,y)是α终边上异于原点的任意一点,, 称为角α的正弦,记作sin α; 称为角α的余弦,记作cos α, 因此sin α=,cos α=; 当角α的终边不在y轴上时, 称为角α的正切,记作tan α,即tan α=, 称为角α的正切,记作cot α,即cot=; 角α的正弦、余弦、正切、余切都称为α的三角函数; 还有正割()、余割(α);
考点二 正切、余切 对角的限制 注意:,其中, ;其中,
考点三 正弦、余弦、 正切、余切 在各象限的符号 口诀:“一全正,二正弦,三正切,四余弦”;
考点四 单位圆 正弦线、余弦线与正切线 一般地,在平面直角坐标系中,坐标满足x2+y2=1的点组成的集合称为单位圆; 正弦线、余弦线与正切线 如果角的终边与单位圆的交点为P, 则P的坐标为. 正弦线与余弦线:过角α终边与单位圆的交点P作x轴的垂线,垂足为M, 当的方向与x轴的正方向相同时,表示cos α是正数,且cos α=, 当的方向与x轴的正方向相反时,表示cos α是负数,且cos α=-, 称为角α的余弦线,类似地,可以直观的表示sin α,称为角α的正弦线
考点五 同角三角比 平方关系 1、→ 或 2、 → 弦与切的转化计算 1、, 2、→ 切与切的转化计算
四基:基础知识、基本技能、基本思想、基本活动经验 【建议用时:40分钟】
第1页
普通高中教科书 数学 必修 第二册(上海教育出版社)
